Построение сечения проходящего через заданную прямую параллельно другой заданной прямой

Разделы: Математика

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

Данный материал характеризуется следующим особенностями:

1. Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.
2. В задачах используются в основном простейшие многогранники.
3. Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного использования.

Чтобы решить задачу построения сечения многогранника ученик должен знать:

• что значит построить сечение многогранника плоскостью;
• как могут располагаться относительно друг друга многогранник и плоскость;
• как задается плоскость;
• когда задача на построение сечения многогранника плоскостью считается решенной.

Поскольку плоскость определяется:

• тремя точками;
• прямой и точкой;
• двумя параллельными прямыми;
• двумя пересекающимися прямыми,

построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.

Существует три основных метода построения сечений многогранников:

1. Метод следов.
2. Метод вспомогательных сечений.
3. Комбинированный метод.

Первые два метода являются разновидностями Аксиоматического метода построения сечений.

Можно также выделить следующие методы построения сечений многогранников:

• построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;
• построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;
• построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;
• построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
• построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.

В федеральный перечень учебников по геометрии для 10-11 класов входят учебники авторов:

• Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б. и др (Геометрия, 10-11);
• Погорелова А.В. (Геометрия, 7-11);
• Александрова А.Д., Вернера А.Л., Рыжик В.И. (Геометрия, 10-11);
• Смирновой И.М. (Геометрия, 10-11);
• Шарыгина И.Ф. (Геометрия, 10-11).

Рассмотрим подробнее учебники Л.С, Атанасяна и Погорелова А.В.

В учебнике Л.С. Атанасяна на тему “Построение сечений многогранников” выделено два часа. В 10 классе в теме “Параллельность прямых и плоскостей” после изучения тетраэдра и параллелепипеда отводится один час на изложение параграфа “Задачи на построение сечений”. Рассматриваются сечения тетраэдра и параллелепипеда. И тема “Параллельность прямых и плоскостей” завершается решением задач на одном или двух часах (всего задач на построение сечений в учебнике восемь).

В учебнике Погорелова А.В. на построение сечений отводится около трех часов в главе “Многогранники”: один – на изучение темы “Изображение призмы и построение ее сечений”, второй – на изучение темы “Построение пирамиды и ее плоских сечений” и третий – на решение задач. В списке задач, приведенных после темы, задач на сечение насчитывается всего около десяти.

Мы предлагаем систему уроков по теме “Построение сечений многогранников” для учебника Погорелова А.В.

Материал предлагается расположить в той последовательности, в какой он может применяться для обучения учащихся. Из изложения темы “Многогранники” предлагается исключить следующие параграфы: “Построение сечений призмы” и “Построение сечений пирамиды” с тем, чтобы систематизировать данный материал в конце этой темы “Многогранники”. Классифицировать его по тематике задач с примерным соблюдением принципа “от простого к сложному” можно весьма условно следующим образом:

1. Определение сечения многогранников.
2. Построение сечений призмы, параллелепипеда, пирамиды методом следов. (Как правило в школьном курсе стереометрии используются задачи на построение сечений многогранников, решаемые основными методами. Остальные методы, в связи с их более высоким уровнем сложности, учитель может оставить для рассмотрения на факультативных занятиях или на самостоятельное изучение. В задачах на построение основными методами требуется построить плоскость сечения, проходящую через три точки).
3. Нахождение площади сечений в многогранниках (без использования теоремы о площади ортогональной проекции многоугольника).
4. Нахождение площади сечений в многогранниках (с применением теоремы о площади ортогональной проекции многоугольника).

СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.

(система уроков и факультативных занятий по теме “Построение сечений многогранников”)

Тема урока: “Построение сечений многогранников”.

Цель урока: ознакомление с методами построений сечений многогранников.

Видео:Сечение, параллельное заданной прямойСкачать

Справочник по геометрии для учащихся 10-х классов

Видео:Построение сечения параллельно прямойСкачать

Построение сечений

Комбинированный метод

Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом.

Полная версия

2011-2022 © Илья Сафонов

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Справочник по геометрии для учащихся 10-х классов

Видео:КАК ПОСТРОИТЬ СЕЧЕНИЕ ТЕТРАЭДРА? #математика #егэматематика #математикапрофильСкачать

Построение сечений

Комбинированный метод

Пример 1

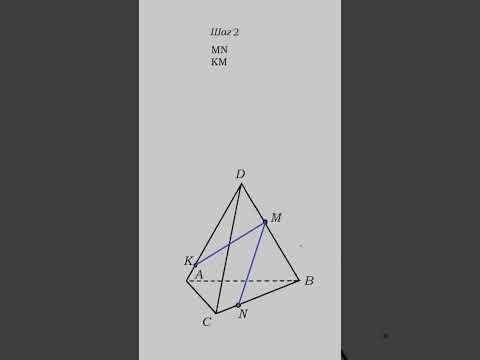
На ребрах AB и AD пирамиды MABCD зададим соответственно точки P и Q — середины этих ребер, а на ребре MC зададим точку R. Построим сечение пирамиды плоскостью, проходящей через точки P, Q и R.

Решение.

Рис. 14

1) Ясно, что основным следом плоскости PQR является прямая PQ.

2) Найдем точку К, в которой плоскость МАС пересекает прямую PQ. Точки К и R принадлежат и плоскости PQR, и плоскости MAC. Поэтому, проведя прямую KR, мы получим линию пересечения этих плоскостей.

3) Найдем точку N=AC BD, проведем прямую MN и найдем точку F=KR MN.

4) Точка F является общей точкой плоскостей PQR и MDB, то есть эти плоскости пересекаются по прямой, проходящей через точку F. Вместе с тем так как PQ — средняя линия треугольника ABD, то PQ параллена BD, то есть прямая PQ параллельна и плоскости MDB. Тогда плоскость PQR, проходящая через прямую PQ, пересекает плоскость MDB по прямой, параллельной прямой PQ, то есть параллельной и прямой BD. Поэтому в плоскости MDB через точку F проведем прямую, параллельную прямой BD.

5) Дальнейшие построения понятны из рисунка. В итоге получаем многоугольник PQD’RB’ — искомое сечение.

Полная версия

2011-2022 © Илья Сафонов

Видео:№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Справочник по геометрии для учащихся 10-х классов

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Построение сечений

Комбинированный метод

I. Построение сечения, проходящего через заданную прямую параллельную другой заданной прямой

Пусть, например, требуется построить сечение многогранника плоскостью @, проходящей через заданную прямую р параллельную второй заданной прямой q. В общем случае решение этой задачи требует некоторых предварительных построений, которые можно выполнять по следующему плану:

1) Через вторую прямую q и какую-нибудь точку W первой прямой p проведем плоскость бетта.

Рис. 15

2) В плоскости бетта через точку W провем прямую q’ параллельную q.

3) Пересекающимися прямыми p и q’ определяется плоскость @. На этом предварительные построения заканчиваются и можно переходить к построению непосредственно сечения многогранника плоскостью @. В некоторых случаях особенности конкретной задачи позволяет осуществить и болле короткий план решения.

Полная версия

2011-2022 © Илья Сафонов

Видео:Построение прямой, параллельной даннойСкачать

Справочник по геометрии для учащихся 10-х классов

Видео:ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать

Построение сечений

Комбинированный метод

I. Построение сечения, проходящего через заданную прямую параллельную другой заданной прямой

На ребрах BC и MA пирамиды MABC зададим соответственно точки P и Q. Потроим сечение пирамиды плоскостью @, проходящей через прямую PQ параллельно прямой AR, точку R, которую зададим следующим образом:
а) на ребре MB;
б) она совпадает с точкой В;
в) в грани MAB.

Решение.

Рис. 16

1) Плоскость, проходящая через вторую прямую, то есть прямую AR, и точку Q, взятую на первой прямой, на изображении уже есть. Это плоскость MAB.

2) В плоскости MAB через точку Q проведем прямую QF параллельную AR.

3) Пересекающимися прямыми PQ и QF определяется плоскость @ (эта плоскость PQF) — плоскость искомого сечения. Построим это сечение методом следов.

4) Точка B совпадает с точкой F’ — проекцией точки F на плоскость ABC (из центра М), а точка A совпадает с точкой Q’ — проекция точки Q на эту плоскость. Тогда точка S’=FQ F’Q’ лежит на основном следе секущей плоскости @. Так как точка P лежит на основном следе секущей плоскости, то прямая S’P — это основной след плоскости @, а отрезок S»P — след плоскости @ на грани ABC. Далее ясно, что точку P следует соединить с точкой F. В итоге получаем четырехугольник PFQS» — искомое сечение.

Полная версия

2011-2022 © Илья Сафонов

Видео:Построение сечений. Метод параллельных прямыхСкачать

Справочник по геометрии для учащихся 10-х классов

Видео:Как строить сечения параллелепипедаСкачать

Построение сечений

Комбинированный метод

I. Построение сечения, проходящего через заданную прямую параллельную другой заданной прямой

На ребрах BC и MA пирамиды MABC зададим соответственно точки P и Q. Потроим сечение пирамиды плоскостью @, проходящей через прямую PQ параллельно прямой AR, точку R, которую зададим следующим образом:
а) на ребре MB;
б) она совпадает с точкой В;
в) в грани MAB.

Решение.

Рис. 17

1) Плоскость, проходящая через прямую AB и точку Р прямой PQ, на изображении уже построена. Это плоскость АВС. Продолжим построение по вышеизложенному плану.

2) В плоскости АВС через точку P проведем прямую PD, параллельную прямой AB.

3) Пересекающимися прямыми PQ и PD определяется плоскость альфа (это плоскость PQD) — плоскость искомого сечения. Построим это сечение.

4) Ясно, что следом плоскости альфа на грани МАС является отрезок DQ.

5) Дальнейшие построения выполним, принимая во внимание следующие соображения. Так как прямая PD параллельна прямой AB, то прямая PD параллельна плоскости МАВ. Тогда плоскость альфа, проходящая через прямую PD, пересекает плоскость МАВ по прямой, параллельной прямой PD, то есть и прямой АВ. Итак, в плоскости МАВ через точку Q проведем прямую QE параллельную АВ. Отрезок QE — это след плоскости альфа на грани МАВ.

6) Соединим точку Р с точкой Е. Отрезок РЕ — это след плоскости альфа на грани МВС. Таким образом, четырехугольник PEQD — искомое сечение.

Полная версия

2011-2022 © Илья Сафонов

Видео:Параллельные прямые циркулемСкачать

Справочник по геометрии для учащихся 10-х классов

Видео:Как строить сеченияСкачать

Построение сечений

Комбинированный метод

I. Построение сечения, проходящего через заданную прямую параллельную другой заданной прямой

На ребрах BC и MA пирамиды MABC зададим соответственно точки P и Q. Потроим сечение пирамиды плоскостью @, проходящей через прямую PQ параллельно прямой AR, точку R, которую зададим следующим образом:
а) на ребре MB;
б) она совпадает с точкой В;
в) в грани MAB.

Решение.

Рис. 18

1) Через вторую прямую AR точку Q первой прямой проведем плоскость. Это плоскость MAR.

2) В плоскости MAR через точку Q проведем прямую QL параллельную AR.

3) Пересекающимися прямыми PQ и QL определяется плоскость альфа (это плоскость PQL) — плоскость искомого сечения. Построим это сечение методом следов. Находим проекции точек Q и L на плоскость ABC. Ясно, что точка Q’ совпадает с точкой А, а точка L’ совпадает с R’=MR BC. Тогда точка S’=LQ L’Q’ лежит на основном следе секущей плоскости альфа. Этим основным следом является прямая S’P, а следом плоскости альфа на грани АВС является отрезок S»P. Далее прямая PL — это след плоскости альфа на рлоскости МВС, а отрезок РN — след плоскости альфа на грани МВС. Итак, четырехугольник PS»QN — искомое сечение.

Полная версия

2011-2022 © Илья Сафонов

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Справочник по геометрии для учащихся 10-х классов

Видео:Как строить сечения тетраэдра и пирамидыСкачать

Построение сечений

Комбинированный метод

I. Построение сечения, проходящего через заданную прямую параллельную другой заданной прямой

На диагоналях АС и C’E’ оснований призмы ABCDEA’B’C’D’E’ зададим соответственно точки P и Q. Построим сечение призмы плоскостью альфа, проходящей через прямую PQ параллельно одной из следующих прямых:
а) АВ;
б) АС’;
в) BC’.

Решение.

Рис. 19

1) Плоскость. проходящая через прямую АВ — вторую заданную прямую и точку Р, взятую на первой прямой, уже построена. Это плоскость АВС.

2) В плоскости АВС через точку Р проведем прямую, параллельно прямой АВ, и найдем точки К и L, в которых эта прямая пересекает соответственно прямые ВС и АЕ.

3) Пересекающимися прямыми PQ и KL определяется плоскость альфа (плоскость KLQ) — плоскость искомого сечения. Построим это сечение, воспользовавшись, в частности, параллельностью оснований призмы.

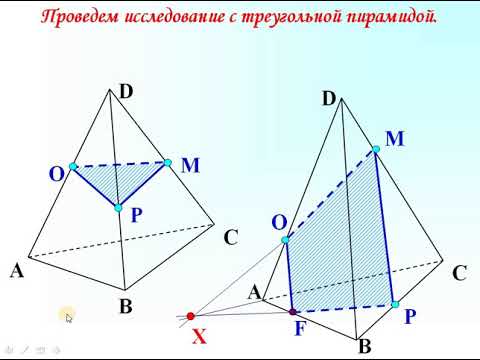
4) Ясно, что прямая KL является основным следом плоскости альфа. Т. к. плоскости призмы параллельны между собой, то линии пересечения секущей плоскости альфа с плоскостями АВС и A’B’C’ также параллельны между собой. Принимая во внимание, что KL параллельна AB и A’B’ параллельна АВ, проведем в плоскости А’B’C’ через точку Q прямую, параллельную прямой A’B’, и найдем точки F и Т, в которых эта прямая пересекает соответственно прямые C’D’ и A’E’. Далее получаем отрезок TL — след плоскости альфа на грани AEE’A’, точку S’=KL CD, прямую S’F — след плоскости альфа на плоскости CDD’ , отрезок FC» — след плоскости альфа на грани CDD’C’ и, наконец, отрезок C»K — след плоскости альфа на грани BCC’B’. В итоге получаем многоугольник KLTFC» — искомое сечение.

Полная версия

2011-2022 © Илья Сафонов

Видео:Построение сечений Занятие 1Скачать

Справочник по геометрии для учащихся 10-х классов

Видео:Профильный ЕГЭ 2023. Задача 13. Построение сечений. Стереометрия. 10 классСкачать

Построение сечений

Комбинированный метод

I. Построение сечения, проходящего через заданную прямую параллельную другой заданной прямой

На диагоналях АС и C’E’ оснований призмы ABCDEA’B’C’D’E’ зададим соответственно точки P и Q. Построим сечение призмы плоскостью альфа, проходящей через прямую PQ параллельно одной из следующих прямых:
а) АВ;
б) АС’;
в) BC’.

Решение.

Рис. 20

1) Проведем плоскость через прямую AC’ — вторую заданную прямую, и точку Р, взятую на первой прямой. Это плоскость ACC’.

2) В плоскости ACC’ через точку Р проведем прямую, параллельную прямой АС’, и найдем точку C», в которой эта прямая пересекает прямую CC’.

3) Пересекающимися прямыми PQ и PC» определяется плоскость альфа (плоскостьC»PQ) — плоскость искомого сечения. Построим это сечение, например, методом следов. Одна точка, принадлежащая следу плоскости альфа на плоскость ABC, которую мы принимаем за основную, на чертеже уже есть. Это точка Р. Найдем еще одну точку этого следа.

4) Проекция точки C» на плоскость АВС является точка С, а проекцией точки Q — точка Q’ — точка пересечения прямой CE с прямой, проходящей в плоскости CEE’ через точку Q параллельно прямой EE’. Точка S’=C»Q CQ’ — это вторая точка основного следа плоскости альфа. Итак, основным следом плоскости альфа является прямая S’P. Она пересекает стороны ВС и АЕ основания призмы соответственно в точках S» и S»’ . Тогда отрезок S»S»’ — след секущей плоскости альфа на грани ABCDE. А отрезок S»C» — след плоскости альфа на грани BCC’B’. Нетрудно увидеть, что прямые C» Q и EE’ лежат в одной плоскости. Найдем точку E» =С»Q EE’. Тогда ясно получение дальнейших следов плоскости альфа:S»’S», S»’T, TF и FC». В итоге получаем многоугольник S»S»’TFC» — искомое сечение.

Полная версия

2011-2022 © Илья Сафонов

Видео:Построение параллельной плоскости на расстояние 30 мм.Скачать

Справочник по геометрии для учащихся 10-х классов

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Построение сечений

Комбинированный метод

I. Построение сечения, проходящего через заданную прямую параллельную другой заданной прямой

На диагоналях АС и C’E’ оснований призмы ABCDEA’B’C’D’E’ зададим соответственно точки P и Q. Построим сечение призмы плоскостью альфа, проходящей через прямую PQ параллельно одной из следующих прямых:
а) АВ;
б) АС’;
в) BC’.

Решение.

Рис. 21

1) Через вторую заданную прямую — пряму BC’ — и, например, через точку Р, лежащую на первой заданной прямой, поведем плоскость. Сделаем это методом следов. Легко устанавливается, что основным следом этой плоскости BC’P является рямая ВР. Затем находим точку S’=BP CD и след S’C’ плоскости BC’P и плоскости CDD’.

2) В плоскости BC’P через точку Р проведем прямую, параллельную прямой BC’. Точку пересечения проведенной прямой с прямой S’C’ обозначим V.

3) Пересекающимися прямыми PQ и PV определяется плоскость альфа (плоскость PQV) — плоскость искомого сечения. Построим это сечение.

4) Находим точки Q’ и V’ — проекции соответственно точек Q и V на плоскость ABC, принимаемую нами за основную плоскость. Затем находим точку S»=QV Q’V’. Это одна из точек основного следа плоскости альфа. И еще одна точка этого следа уже есть. Это заданная точка Р. Итак, прямая S»P — основной след плоскости альфа, а полученный при этом отрезок S»’S»» — след плоскости альфа на грани АВСDE. Дальнейший ход построения ясен: S»»’=S»P CD, S»»’V, точки C»=S»»’V CC’ и F=S»»’V C’D’, затем FQ и точка T=FQ A’E’ и, наконец, TS»». В итоге получаем многоугольник S»’C»FTS»» — искомое сечение.

Полная версия

2011-2022 © Илья Сафонов

Видео:ПОСТРОЕНИЕ СЕЧЕНИЙ ТЕТРАЭДРА ПЛОСКОСТЬЮСкачать

Справочник по геометрии для учащихся 10-х классов

Видео:Построение сечений методом внутреннего проецированияСкачать

Построение сечений

Комбинированный метод

I. Построение сечения, проходящего через заданную прямую параллельную другой заданной прямой

На диагоналях АС и C’E’ оснований призмы ABCDEA’B’C’D’E’ зададим соответственно точки P и Q. Построим сечение призмы плоскостью альфа, проходящей через прямую PQ параллельно одной из следующих прямых:
а) АВ;
б) АС’;
в) BC’.

Решение.

Рис. 22

Замечание: Наметим кратко ход решения примера 3,в, при котором на первой заданной прямой была взята точка Q, а не точка P (рисунок 22).

1) Строим плоскость BC’Q (это плоскость BC’E’).

2) Плоскость BC’Q пересекает плоскость ABC по прямой BN параллельной C’E’ (для построения можно воспользоваться тем, что BN параллельна СЕ).

3) В плоскости BC’Q через точку Q проводим прямую QM параллельную BC’ (М=QM BN).

4) Строим сечение призмы плоскостью, определяемой пересекающимися прямыми PQ и QM. Это можно сделать в следующем порядке: MP, S’=MP AE и S»=МР ВС, S»»=MP CE, C»=S»»Q CC’, S»’C», F=S»’C» C’D’, FQ, T=FQ A’E’, TS’.Многоугольник S»C»FTS’- искомое сечение.

Полная версия

2011-2022 © Илья Сафонов

Справочник по геометрии для учащихся 10-х классов

Построение сечений

Комбинированный метод

II. Построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым

Пусть требуется построить сечение многогранника плоскостью, проходящей через заданную точку К параллельно двум заданным скрещивающимся прямым l и m. При решении задач этого вида можно применять следующий план построения:

1) Выберем некоторую точку W. (Эта точка может лежать на одной из заданных скрещивающихся прямых, может совпадать с точкой К.)

2) Через точку W проведем прямые l’ и m’. (Естественно, если точка W лежит на одной из прямых, например на прямой l, то прямая l’ совпадает с прямой l.)

3) Пересекающимися прямыми l’ и m’ определяется плоскость бетта — плоскость вспомогательного сечения многогранника. Строим сечение многогранника плоскостью бетта.

4) Построим сечения многогранника плоскостью альфа, проходящей через точку K, параллельно плоскости бетта.

Полная версия

2011-2022 © Илья Сафонов

Справочник по геометрии для учащихся 10-х классов

Построение сечений

Комбинированный метод

II. Построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым

На ребрах AD и С’D’ призмы ABCDA’В’С’D’, зададим соответственно точки P и Q, а на ребре DD’ зададим точку К. Построим сечение призмы плоскостью альфа, проходящей через точку К параллельно прямой PQ и одной из следующих прямых:
а) АВ;
б) А’В;
в) BR, точку R которой зададим на ребре A’D’.

Решение.

Рис. 23

1) Пусть точка W совпадает с точкой P.

2) В плоскости АВС через точку P проведем прямую, параллельную прямой АВ. Найдем точку Е, в которой проведенная прямая пересекает прямую ВС.

3) Пересекающимися прямыми PQ и PE определяется плоскость бетта — плоскость вспомогательного сечения. Построим сечение призмы плоскостью бетта. Прямая PE является ее основным следом. Находим точку S, в которой прямая СD пересекается со следом PE. Затем строим прямую SQ — след плоскости бетта на плоскости CDD’ и точки С» и D» — следы плоскости бетта соответственно на прямых СС’ и DD’. Затем строим прямую D»Р и получаем точку F на ребре А’D’. Таким образом, сечением призмы плоскостью бетта является многоугольник РЕС»QF.

4) Строим теперь сечение призмы плоскостью альфа, проходящей через точку К параллельно плоскости бетта. В итоге получаем треугольник KLN — искомое сечение.

Полная версия

2011-2022 © Илья Сафонов

Справочник по геометрии для учащихся 10-х классов

Построение сечений

Комбинированный метод

II. Построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым

На ребрах AD и С’D’ призмы ABCDA’В’С’D’, зададим соответственно точки P и Q, а на ребре DD’ зададим точку К. Построим сечение призмы плоскостью альфа, проходящей через точку К параллельно прямой PQ и одной из следующих прямых:
а) АВ;
б) А’В;
в) BR, точку R которой зададим на ребре A’D’.

Решение.

Рис. 24

1) Пусть точка W совпадает с точкой Q. Чтобы через точку Q провести прямую, параллельную прямой А’В, сначала через прямую А’В и точку Q проведем плоскость гамма. Сделаем это так. Найдем точку Q’ — проекцию точки Q на плоскость АВС и проведем прямую AQ’. Ясно, что AQ’ параллельно A’Q. Теперь через точку В в плоскости АВС проведем прямую l’ параллельно AQ’. Пересекающимися прямыми А’В и l’ определяется плоскость гамма. В плоскости гамма через точку Q проведем прямую l» параллельно A’В.

2) Пересекающимися прямыми PQ и l», определяется плоскость бетта — плоскость вспомогательного сечения призмы. Построим это сечение. Находим для этого точку S’=l’ пересекается l», а затем прямую PS’ — основной след плоскости бетта. Находим далее точку s»=PS’ пересекается CD и проводим прямую S»Q — след плоскости бетта на плоскости CDD’. Получаем точку D» — след плоскости бетта на прямой DD’. Точка D» и точка Р лежат в плоскости ADD’. Поэтому прямая PD»— след плоскости бетта на плоскости АDD’, а отрезок PF — след плоскости бетта на грани ADD’A’. Таким образом, сечением призмы плоскостью бетта является четырехугольник РS»QF. (Обратите внимание: QF параллельно PS». И это, естественно, так. Ведь основания призмы лежат в параллельных плоскостях. Этим обстоятельством можно было воспользоваться при построении сечения призмы плоскостью бетта.)

3) Теперь строим сечение призмы плоскостью альфа, проходящей через точку К параллельно плоскости бетта. Это построение выполнить уже несложно. В итоге получаем треугольник KLN — искомое сечение.

Существует 2 основных метода построения сечений многогранников

Существует 2 основных метода построения сечений многогранников

Существует 2 основных метода построения сечений многогранников:

1) Аксиоматический метод

а) Метод следов

б) Метод вспомогательных сечений

2) Комбинированный метод

Аксиоматический метод построения сечений

1. Метод следов

На ребрах АА’ и В’С’ призмы АВСА’В’С’ зададим соответственно точку P и Q. Построим сечение призмы плоскостью (PQR), точку R которой зададим в одной из следующих граней:
а) ВССВ’С’;
б) А’В’С’;
в) АВС

Решение.

а) 1) Так как точки Q и R лежат в плоскости (ВСС’), то в этой плоскости лежит прямая QR. Проведем ее. Это след плоскости (PQR) на плоскость(ВСС’). (рис.1)

2) Находим точки В» и С’, в которых прямая QR пересекает соответственно прямые ВВ’ и СС’. Точки В’ и С’ — это следы плоскости (PQR) соответственно на прямых ВВ’ и СС’.

3) Так как точки В» и Р лежат в плоскости (АВВ’), то прямая »Рлежит в этой плоскости. Проведем ее. Отрезок В**Р — след плоскости (PQR) на грани АВВ’А’.

4) Так как точки Р и С лежат в плоскости (АСС’), то прямая РС» лежит в этой плоскости. Проведем ее. Это след плоскости (PQR) на плоскости (АСС’).

5) Находим точку V, в которой прямая РС» пересекает ребро А’С’. Это след плоскости (PQR) на ребре А’С’.

6) Тачка как точки Q и V лежат в плоскости (А’В’С’), то прямая QV лежит в этой плоскости. Проведем прямую QV. Отрезок QV — след плоскости (PQR) на грани АВС. Итак, мы получили многоугольник QB»PV — искомое сечение.

б) 1) Так как точки Q и R лежат в плоскости (А’В’С’), то в этой плоскости лежит прямая QR. Проведем ее. Это след плоскости (PQR) на плоскости (А’В’С’).(рис.2)

2) Находим точки D’ и Е’, в которых прямая QR пересекает соответственно прямые А’В’ и B’С’. Так как точка D’ лежит на ребре А’В’, отрезок QD’ — след плоскости (PQR) на грани А’В’С’.

3) Так как точки D’ и P лежат в плоскости (АВВ’), то прямая D’P лежит в этой плоскости. Проведем ее. Это след плоскости (PQR) на плоскости (АВВ’), а отрезок D’P — след плоскости (PQR) на грани АВВ’А’.

4) Так как точки Р и Е’ лежат в плоскости (АСС’), то в этой плоскости лежит прямая РЕ’. Проведем ее. Это след плоскости (PQR) на плоскости (АСС’).

5) Находим точку С»=PE»CC’. Так как точка С» лежит на ребре СС’, то отрезок РС» — это след плоскости (PQR) на грани АСС’А’.

6) Так как точки Q и С» лежат в плоскости (ВСС’), то прямая QC» лежит в этой плоскости. Проведем ее. Это след плоскости (PQR) на плоскости (ВСС’), а отрезок QC»- след плоскости (PQR) на грани ВСС’В’. Итак, мы получили многоугольник QD’РС» — это и есть искомое сечение.

в) 1) Из трех заданных точек Р, Q и R никакие две не лежат в какой-нибудь одной из плоскостей граней призмы, поэтому найдем основной след плоскости (PQR) (т. е. линию пересечения плоскости (PQR) с плоскостью (АВС), выбранной в качестве основной). Для этого сначала найдем проекции точек Р, Q и R на плоскость (АВС) в направлении, параллельном боковому ребру призмы. Так как точка Р лежит на ребре АА’, то точка Р’ совпадает с точкой А. Так как точка Q лежит в плоскости (ВСС’), то в этой плоскости через точку Q проведем прямую, параллельную прямой ВВ’, и найдем точку Q’, в которой проведенная прямая пересекает прямую ВС. Так как точка R по условию лежит в плоскости, выбранной в качестве основной, то точка R’ совпадает с точкой R.(Рис.3)

2) Параллельными прямыми РР’ и QQ’ определяется плоскость. Проведем в этой плоскости прямые PQ и Р’Q’ и найдем точку S=PQ пересекает P’Q’. Так как точка S’ лежит на прямой PQ, то она лежит в плоскости (PQR), и так как точка S’ лежит на прямой Р’Q’, то она лежит в плоскости (АВС). Таким образом, точка S’ является общей точкой плоскостей (PQR) и (АВС). Это значит, что плоскости (PQR) и (АВС) пересекаются по прямой, проходящей через точку S’.

3) Так как точка R совпадает с точкой R’, то точка R — это еще одна общая точка плоскостей (PQR) и (АВС). Таким образом, прямая S’R — основной след плоскости (PQR). Проведем эту прямую. Как видим из рисунка, прямая S’R пересекает ребра АВ и ВС основания призмы соответственно в точках S’ ‘и S»’.

4) Так как точки S»’ и Q лежат в плоскости (ВСС’), то прямая S»’ Q лежит в этой плоскости. Проведем ее. Это след плоскости (PQR) на плоскости (ВСС’). А отрезок S»’ Q, — след плоскости (PQR) на грани ВСС’В’.

5) Аналогично находим отрезок S» Р — след плоскости (PQR) на грани АВВ’А’.

6) Находим далее точку С,= S»’ Q СС’. Так как точки С» и Р лежат в плоскости (АСС’), то прямая ѻРлежит в плоскости (АСС’). Проведем эту прямую, являющуюся следом плоскости (PQR) на плоскости (АСС’).

7) Находим точку F=PC» пересекает A’С’ и получаем затем отрезок PF — след плоскости (PQR) на грани АСС’А’.

8) Точки Q и F лежат в плоскости А’В’C’, поэтому прямая QF лежит в плоскости (А’В’C’). Проведем прямую QF, получим отрезок QF — след плоскости (PQR) на грани А’В’C’. Итак, мы получили многоугольник QS»’S»PF — искомое сечение.

3 а м е ч а н и е. Покажем другой путь нахождения точки С», при котором не находим точку пересечения прямой S»’ Q с прямой С’С». Будем рассуждать следующим образом. Если следом плоскости (PQR) на прямой СС’ является некоторая точка V, то ее проекция на плоскость (АВС) совпадает с точкой С. Тогда точка S»»= V’P ‘пересекает VP лежит на основном следе S’R плоскости (PQR). Строим эту точку S»» как точку пересечения прямых V’P’ (это прямая СА) и S’R. А далее проводим прямую S»»Р. Она пересекает прямую СС’ в точке V.

Пример 2.

На ребре МВ пирамиды МАВСD зададим точку Р, на ее грани MCD зададим точку Q. Построим сечение пирамиды плоскостью (PQR), точку R которой зададим:
а) на ребре МС;
б) на грани МАD;
в) в плоскости (МАС), вне пирамиды.

Решение.

a) Следом плоскости (PQR) на грани МВС является отрезок РR, а ее следом на грани MCD является отрезок RD’, где точка D’ — это точка пересечения прямой RQ с ребром МD. Ясно, что плоскость (PQR) имеет следы на гранях MAD и МАВ (так как с этими гранями плоскость (PQR) имеет общие точки). Найдем след плоскости (PQR) на прямой МА. Сделаем это следующим образом:

1) Построим точки Р’, Q’ и R’ — проекции точек Р, Q и R из центра М на плоскость (АВС), принимаемую, таким образом, за основную плоскость. (Рис. 4)

2) Далее построим точки S’= РQ пересекает Р’Q’ и S» = PR пересекает P’R’ и проведем прямую S’ S» — основной след плоскости (PQR).

3) Если плоскость (PQR) пересекает прямую МА в некоторой точке V, то точка V’ совпадает с точкой А и точка S»’= VQ пересекает V’Q’ лежит на прямой S’ S». Другими словами, в точке S»’ пересекаются три прямые: VQ,, V’Q» и S’ S». Две последние прямые из этих трех на чертеже уже есть. Поэтому точку S»’ мы построим как точку пересечения прямых V’Q’ и SS».

4) Проведем прямую QS»’ (она совпадает с прямой VQ, так как прямая VQ должна проходить через точку S»’, т. е. точки V, Q и S»’ лежат на одной прямой).

5) Находим точку V, в которой прямая QS» ‘пересекает прямую МА, Точка V — это след плоскости (PQR) на ребре МА. Далее ясно, что отрезки PV и VD’ — следы плоскости (PQR) соответственно на гранях МАВ и MAD. Таким образом, многоугольник PRD’V — искомое сечение.

б) 1) Принимаем плоскость (АВС) за основную плоскость и строим точки P’, Q’ и R’ — проекции соответственно точек Р, Q и R на плоскость (АВС). Центром этого внутреннего проектирования является точка М.(Рис.5.)

2) Строим прямую S’S» — основной след плоскости (PQR).

3) Если плоскость (PQR) пересекает прямую МА в точке V, то точка V’ — проекция точки V на плоскость (АВС) из центра М— совпадает с точкой А, а прямые S’S», V’R’ и прямая VR, точка V которой пока нами не построена, пересекаются в точке S»’. Находим эту точку S»’=V’R’ пересекается S’S» .

4) Проводим прямую RS»’, и находим точку V=RS»’ пересекается MA. Дальнейшее построение ясно. Искомым сечением является многоугольник PVD’Т.

(Рис.6.) Пусть точка R расположена в плоскости (МАС) так, как это показано на рисунке 6.

1) Принимаем плоскость (АВС) за основную плоскость и строим точки P’, Q’ и R’ — проекции соответственно точек P, Q и R на плоскость (ABC). (центром проектирования является точка М.)

2) Строим прямую S’S», — основной след плоскости (PQR).

3) Находим точку V — след плоскости (PQR) на прямой МА. Точка V’ — проекция точки V на плоскость (АВС) из центра М— совпадает в этом случае с точкой А.

4) Находим точку S»’= P’V’ пересекается S’S», а затем и точку V =PS»’ пересекается МА.

5) Получаем след РV плоскости (PQR) на плоскости (МАВ).

6) Находим точку T — след плоскости (PQR) на прямой МО. Ясно, что точка Т’ в этом случае совпадает с точкой D. Для построения точки T строим точку S»»=Q’T’ пересекается S’S», а затем точку T = QS»’ ‘пересекается MT’.

7) Совокупность следов PV, VT, ТС’, и С’P, т. е. многоугольник PVTC’ — искомое сечение.

Комбинированный метод построения сечений

Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом.

Пример№1.

На ребрах AB и AD пирамиды MABCD зададим соответственно точки P и Q — середины этих ребер, а на ребре MC зададим точку R. Построим сечение пирамиды плоскостью, проходящей через точки P, Q и R.

Решение

1). Ясно, что основным следом плоскости PQR является прямая PQ.

2). Найдем точку К, в которой плоскость МАС пересекает прямую PQ. Точки К и R принадлежат и плоскости PQR, и плоскости MAC. Поэтому, проведя прямую KR, мы получим линию пересечения этих плоскостей.

3). Найдем точку N=AC BD, проведем прямую MN и найдем точку F=KR MN.

4). Точка F является общей точкой плоскостей PQR и MDB, то есть эти плоскости пересекаются по прямой, проходящей через точку F. Вместе с тем так как PQ — средняя линия треугольника ABD, то PQ параллена BD, то есть прямая PQ параллельна и плоскости MDB. Тогда плоскость PQR, проходящая через прямую PQ, пересекает плоскость MDB по прямой, параллельной прямой PQ, то есть параллельной и прямой BD. Поэтому в плоскости MDB через точку F проведем прямую, параллельную прямой BD.

5). Дальнейшие построения понятны из рисунка. В итоге получаем многоугольник PQD’RB’ — искомое сечение.

1. Построение сечения, проходящего через заданную прямую параллельную другой заданной прямой.

Пусть, например, требуется построить сечение многогранника плоскостью @, проходящей через заданную прямую р параллельную второй заданной прямой q. В общем случае решение этой задачи требует некоторых предварительных построений, которые можно выполнять по следующему плану:

1). Через вторую прямую q и какую-нибудь точку W первой прямой p проведем плоскость бетта (рис.

2). В плоскости бетта через точку W проведем прямую q’ параллельную q.

3). Пересекающимися прямыми p и q’. Определяется плоскость @. На этом предварительные построения заканчиваются и можно переходить к построению непосредственно сечения многогранника плоскостью @. В некоторых случаях особенности конкретной задачи позволяет осуществить и болле короткий план решения. Рассмотрим примеры.

Пример№2.

На ребрах BC и MA пирамиды MABC зададим соответственно точки P и Q. Построим сечение пирамиды плоскостью @, проходящей через прямую PQ параллельно прямой AR, точку R, которую зададим следующим образом: а). На ребре MB; б). Она совпадает с точкой В; в). В грани MAB.

Решение:

.(рисунок Плоскость, проходящая через вторую прямую, то есть прямую AR, и точку Q, взятую на первой прямой, на изображении уже есть. Это плоскость MAB.

2). В плоскости MAB через точку Q проведем прямую QF параллельную AR.

3). Пересекающимися прямыми PQ и QF определяется плоскость @ (эта плоскость PQF) — плоскость искомого сечения. Построим это сечение методом следов.

4). Точка B совпадает с точкой F’ — проекцией точки F на плоскость ABC (из центра М), а точка A совпадает с точкой Q’ — проекция точки Q на эту плоскость. Тогда точка S’=FQ F’Q’ лежит на основном следе секущей плоскости @. Так как точка P лежит на основном следе секущей плоскости, то прямая S’P — это основной след плоскости @, а отрезок S»P — след плоскости @ на грани ABC. Далее ясно, что точку P следует соединить с точкой F. В итоге получаем четырехугольник PFQS» — искомое сечение.

(рисунокПлоскость, проходящая через прямую AB и точку Р прямой PQ, на изображении уже построена. Это плоскость АВС. Продолжим построение по вышеизложенному плану.

2). В плоскости АВС через точку P проведем прямую PD, параллельную прямой AB.

3). Пересекающимися прямыми PQ и PD определяется плоскость альфа (это плоскость PQD) — плоскость искомого сечения. Построим это сечение.

4). Ясно, что следом плоскости альфа на грани МАС является отрезок DQ.

5). Дальнейшие построения выполним, принимая во внимание следующие соображения. Так как прямая PD параллельна прямой AB, то прямая PD параллельна плоскости МАВ. Тогда плоскость альфа, проходящая через прямую PD, пересекает плоскость МАВ по прямой, параллельной прямой PD, то есть и прямой АВ. Итак, в плоскости МАВ через точку Q проведем прямую QE параллельную АВ. Отрезок QE — это след плоскости альфа на грани МАВ.

6). Соединим точку Р с точкой Е. Отрезок РЕ — это след плоскости альфа на грани МВС. Таким образом, четырехугольник PEQD — искомое сечение.

(рисунок1Через вторую прямую AR точку Q первой прямой проведем плоскость. Это плоскость MAR.

2).В плоскости MAR через точку Q проведем прямую QL параллельную AR.

3). Пересекающимися прямыми PQ и QL определяется плоскость альфа (это плоскость PQL) — плоскость искомого сечения. Построим это сечение методом следов. Находим проекции точек Q и L на плоскость ABC. Ясно, что точка Q’ совпадает с точкой А, а точка L’ совпадает с R’=MR BC. Тогда точка S’=LQ L’Q’ лежит на основном следе секущей плоскости альфа. Этим основным следом является прямая S’P, а следом плоскости альфа на грани АВС является отрезок S»P. Далее прямая PL — это след плоскости альфа на плоскости МВС, а отрезок РN — след плоскости альфа на грани МВС. Итак, четырехугольник PS»QN — искомое сечение.

Пример 3.

На диагоналях АС и C’E’ оснований призмы ABCDEA’B’C’D’E’ зададим соответственно точки P и Q. Построим сечение призмы плоскостью альфа, проходящей через прямую PQ параллельно одной из следующих прямых: а). АВ; б). АС’; в). BC’ Решение:

(рисунок Плоскость. проходящая через прямую АВ — вторую заданную прямую и точку Р, взятую на первой прямой, уже построена. Это плоскость АВС.

2). В плоскости АВС через точку Р проведем прямую, параллельно прямой АВ, и найдем точки К и L, в которых эта прямая пересекает соответственно прямые ВС и АЕ.

3). Пересекающимися прямыми PQ и KL определяется плоскость альфа (плоскость KLQ) — плоскость искомого сечения. Построим это сечение, воспользовавшись, в частности, параллельностью оснований призмы.4). Ясно, что прямая KL является основным следом плоскости альфа. Т. к. плоскости призмы параллельны между собой, то линии пересечения секущей плоскости альфа с плоскостями АВС и A’B’C’ также параллельны между собой. Принимая во внимание, что KL параллельна AB и A’B’ параллельна АВ, проведем в плоскости А’B’C’ через точку Q прямую, параллельную прямой A’B’, и найдем точки F и Т, в которых эта прямая пересекает соответственно прямые C’D’ и A’E’. Далее получаем отрезок TL — след плоскости альфа на грани AEE’A’, точку S’=KL CD, прямую S’F — след плоскости альфа на плоскости CDD’ , отрезок FC» — след плоскости альфа на грани CDD’C’ и, наконец, отрезок C»K — след плоскости альфа на грани BCC’B’. В итоге получаем многоугольник KLTFC» — искомое сечение.

(рисунок Проведем плоскость через прямую AC’ — вторую заданную прямую, и точку Р, взятую на первой прямой. Это плоскость ACC’.

2). В плоскости ACC’ через точку Р проведем прямую, параллельную прямой АС’, и найдем точку C», в которой эта прямая пересекает прямую CC’.

3). Пересекающимися прямыми PQ и PC» определяется плоскость альфа (плоскость C»PQ) — плоскость искомого сечения. Построим это сечение, например, методом следов. Одна точка, принадлежащая следу плоскости альфа на плоскость ABC, которую мы принимаем за основную, на чертеже уже есть. Это точка Р. Найдем еще одну точку этого следа.

4). Проекция точки C» на плоскость АВС является точка С, а проекцией точки Q — точка Q’ — точка пересечения прямой CE с прямой, проходящей в плоскости CEE’ через точку Q параллельно прямой EE’. Точка S’=C»Q CQ’ — это вторая точка основного следа плоскости альфа. Итак, основным следом плоскости альфа является прямая S’P. Она пересекает стороны ВС и АЕ основания призмы соответственно в точках S» и S»’ . Тогда отрезок S»S»’ — след секущей плоскости альфа на грани ABCDE. А отрезок S»C» — след плоскости альфа на грани BCC’B’. Нетрудно увидеть, что прямые C» Q и EE’ лежат в одной плоскости. Найдем точку E» =С»Q EE’. Тогда ясно получение дальнейших следов плоскости альфа: S»’S», S»’T, TF и FC». В итоге получаем многоугольник S»S»’TFC» — искомое сечение.

(рисунокЧерез вторую заданную прямую — прямую BC’ — и, например, через точку Р, лежащую на первой заданной прямой, поведем плоскость. Сделаем это методом следов. Легко устанавливается, что основным следом этой плоскости BC’P является прямая ВР. Затем находим точку S’=BP CD и след S’C’ плоскости BC’P и плоскости CDD’.

2).В плоскости BC’P через точку Р проведем прямую, параллельную прямой BC’. Точку пересечения проведенной прямой с прямой S’C’ обозначим V.

3). Пересекающимися прямыми PQ и PV определяется плоскость альфа (плоскость PQV) — плоскость искомого сечения. Построим это сечение.

4). Находим точки Q’ и V’ — проекции соответственно точек Q и V на плоскость ABC, принимаемую нами за основную плоскость. Затем находим точку S»=QV Q’V’. Это одна из точек основного следа плоскости альфа. И еще одна точка этого следа уже есть. Это заданная точка Р. Итак, прямая S»P — основной след плоскости альфа, а полученный при этом отрезок S»’S»» — след плоскости альфа на грани АВСDE. Дальнейший ход построения ясен: S»»’=S»P CD, S»»’V, точки C»=S»»’V CC’ и F=S»»’V C’D’, затем FQ и точка T=FQ A’E’ и, наконец, TS»». В итоге получаем многоугольник S»’C»FTS»» — искомое сечение.

Замечание: Наметим кратко ход решения примера 3,в, при котором на первой заданной прямой была взята точка Q, а не точка P (рисунок 22).

1). Строим плоскость BC’Q (это плоскость BC’E’).

2). Плоскость BC’Q пересекает плоскость ABC по прямой BN параллельной C’E'(для построения можно воспользоваться тем, что BN параллельна СЕ).

3). В плоскости BC’Q через точку Q проводим прямую QM параллельную BC’ (М=QM BN).

4). Строим сечение призмы плоскостью, определяемой пересекающимися прямыми PQ и QM. Это можно сделать в следующем порядке: MP, S’=MP AE и S»=МР ВС, S»»=MP CE, C»=S»»Q CC’, S»’C», F=S»’C» C’D’, FQ, T=FQ A’E’, TS. Многоугольник S»C»FTS’- искомое сечение.

2. Построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым.

Пусть требуется построить сечение многогранника плоскостью, проходящей через заданную точку К параллельно двум заданным скрещивающимся прямым l и m. При решении задач этого вида можно применять следующий план построения:

1.Выберем некоторую точку W. (Эта точка может лежать на одной из заданных скрещивающихся прямых, может совпадать с точкой К.)

2.Через точку W проведем прямые l’ и m’. (Естественно, если точка W лежит на одной из прямых, например на прямой l, то прямая l’ совпадает с прямой l.)

3. Пересекающимися прямыми l’ и m’ определяется плоскость бетта — плоскость вспомогательного сечения многогранника. Строим сечение многогранника плоскостью бетта.

4. Построим сечения многогранника плоскостью альфа, проходящей через точку K, параллельно плоскости бетта.

Рассмотрим примеры применения изложенного плана.

П р и м е р 4.

На ребрах AD и С’D’ призмы ABCDA’В’С’D’, зададим соответственно точки P и Q, а на ребре DD’ зададим точку К. Построим сечение призмы плоскостью альфа, проходящей через точку К параллельно прямой PQ и одной из следующих прямых: а) АВ; б) А’В; в) BR, точку R которой зададим на ребре A’D’.

Решение. a)

(Рис. 2Пусть точка W совпадает с точкой P.

2) В плоскости АВС через точку P проведем прямую, параллельную прямой АВ. Найдем точку Е, в которой проведенная прямая пересекает прямую ВС.

3) Пересекающимися прямыми PQ и PE определяется плоскость бетта — плоскость вспомогательного сечения. Построим сечение призмы плоскостью бетта. Прямая PE является ее основным следом. Находим точку S, в которой прямая СD пересекается со следом PE. Затем строим прямую SQ — след плоскости бетта на плоскости CDD’ и точки С» и D» — следы плоскости бетта соответственно на прямых СС’ и DD’. Затем строим прямую D»Р и получаем точку F на ребре А’D’. Таким образом, сечением призмы плоскостью бетта являет — я многоугольник РЕС»QF.

4) Строим теперь сечение призмы плоскостью альфа, проходящей через точку К параллельно плоскости бетта. В итоге получаем треугольник KLN — искомое сечение.

(Рис. Пусть точка W совпадает с точкой Q. Чтобы через точку Q провести прямую, параллельную прямой А’В, сначала через прямую А’В и точку Q проведем плоскость гамма. Сделаем это так. Найдем точку Q’ — проекцию точки Q на плоскость АВС и проведем прямую AQ’. Ясно, что AQ’ параллельно A’Q. Теперь через точку В в плоскости АВС проведем прямую l’ параллельно AQ’. Пересекающимися прямыми А’В и l’ определяется плоскость гамма. В плоскости гамма через точку Q проведем прямую l» параллельно A’В.

3) Пересекающимися прямыми PQ и l», определяется плоскость бетта — плоскость вспомогательного сечения призмы. Построим это сечение. Находим для этого точку S’=l’ пересекается l», а затем прямую PS’ — основной след плоскости бетта. Находим далее точку s»=PS’ пересекается CD и проводим прямую S»Q — след плоскости бетта на плоскости CDD’. Получаем точку D» — след плоскости бетта на прямой DD’. Точка D» и точка Р лежат в плоскости ADD’. Поэтому прямая PD»— след плоскости бетта на плоскости АDD’, а отрезок PF — след плоскости бетта на грани ADD’A’. Таким образом, сечением призмы плоскостью бетта является четырехугольник РS»QF. (Обратите внимание: QF параллельно PS». И это, естественно, так. Ведь основания призмы лежат в параллельных плоскостях. Этим обстоятельством можно было воспользоваться при построении сечения призмы плоскостью бетта.)

4) Теперь строим сечение призмы плоскостью альфа, проходящей через точку К параллельно плоскости бетта. Это построение выполнить уже несложно. В итоге получаем треугольник KLN — искомое сечение.

(Рис. В качестве точки W выберем точку Q.

2) Через прямую BR и точку Q проведем плоскость гамма. Плоскость гамма пересекает плоскость АВС по прямой l’ параллельно QR. Для построения прямой l’ строим точки R’ и Q’ — проекции соответственно точек R и Q на плоскость АВС — и проводим прямую Q’R’, а затем в плоскости АВС через точку В проводим прямую l’ параллельно Q’R’. В плоскости гамма через точку Q проводим прямую l» параллельно BR. Получим точку S’=l’ пересекается l».

3) Пересекающимися прямыми PQ и l» определяется плоскость бетта — плоскость вспомогательного сечения призмы. Построим это сечение. Ясно, что прямая PS’ является основным следом плоскости бетта. Находим далее точки S»= PS’ пересекается CD, S»’= РS’ пересекается BC и C» = QS» пересекается CC’. Получим отрезки РS»’, S»’C» и C»Q— следы плоскости бетта соответственно на гранях ABCD, ВСС’В и CDD’С’. Далее либо проведем в плоскости А’В’С’ прямую, параллельную следу PS’, и получим точку F, либо найдем точку D»=S»Q пересекается DD’ и проведем прямую D»Р. Эта прямая пересечет прямую А’D’ в точке F. Получаем, таким образом, еще два следа плоскости бетта: QF н FP. Итак, многоугольник PS»’C»QF — сечение призмы плоскостью бетта.

4) Теперь построим сечение призмы плоскостью альфа, проходящей через точку К параллельно плоскости бетта. В итоге получаем треугольник KLN — искомое сечение.

П р и м е р 5.

На ребрах МВ и МА пирамиды МАВСD зададим соответственно точки Р и К, и на отрезке АС зададим точку Q. Построим сечение пирамиды плоскостью альфа, проходящей через точку К параллельно прямой PQ и одной из следующих прямых: а) CD; б) МС; в) RV, точки R и V которой зададим соответственно на ребрах АВ и МС пирамиды.

Р е ш е н и е.

(Рис. 2В плоскости ABC через точку Q проведем прямую, параллельную прямой CD, и. найдем точки S’. S» и S»’, в которых эта прямая пересекает соответственно прямые BC, АD и АВ.

2) Пересекающимися прямыми PQ и S’S» определяется плоскость бетта — плоскость вспомогательного сечения пирамиды. Построим это сечение. Основным следом плоскости бетта является прямая S’S». Отрезок PS’ — след плоскости бетта на грани МВС, прямая PS»’ — ее след на плоскости МАВ, отрезок PA’ — на грани МАВ, отрезок А’S»— на грани MAD.

3) Строим далее сечение пирамиды плоскостью @, проходящей через точку К параллельно плоскости бетта. В итоге получаем многоугольник КВ’C’D’ — искомое сечение.

(Рис. 27.) Выполним построение заданного сечения в следующем порядке:

1) В плоскости МАС через точку Q проведем прямую QA параллельно MC

2) Построим вспомогательное сечение пирамиды плоскостью, которая определяется пересекающимися прямыми PQ и QA’. С этой целью найдем точку S’=PA’ пересекается АВ, проведем прямую S’Q, являющуюся основным следом плоскости PQA’, получим точки S»=S’Q пересекается AD и S»’=S’Q пересекается BC и соединим точку А’ с точкой S», а точку P с точкой S»’. Четырехугольник PA’S»S»’ — это вспомогательное сечение пирамиды. Плоскость этого сечения параллельна прямым PQ и МС, но не проходит через точку К.

3) Теперь построим сечение пирамиды плоскостью, проходящей через точку К параллельно плоскости PQA’. В итоге получаем четырехугольник В’KFE — искомое сечение.

(Рис. 28.) Выполним построение заданного сечения пирамиды, построив сначала вспомогательное сечение ее плоскостью, проходящей через прямую PQ параллельно прямой RV. Сделаем это в следующем порядке:

1) Построим точку S’=PV пересекается BC и проведем прямую S’R.

2) Пересекающимися прямыми S’V и S’R определяется плоскость. В этой плоскости через точку Р проведем прямую PS» параллельно RV.

3) Пересекающимися прямыми PQ и PS» определяется плоскость вспомогательного сечения пирамиды. Построим это сечение. Находим последовательно прямую S»Q — основной след плоскости вспомогательного сечения, затем точки Т’=S»Q пересекается ВС, Т»=S»Q пересекается АB и Т»’=S»Q пересекается CD, Проведем далее прямую Т’P и найдем точку Е= Т’P пересекается ‘MC. Точку P соединим с точкой Т», а точку Е — с Т»’. Четырехугольник PT»Т»’Е — вспомогательное сечение пирамиды. Плоскость этого сечения параллельна прямым PQ и RV, но не проходит через точку К. Теперь построим сечение пирамиды плоскостью, проходящей через точку К параллельно плоскости вспомогательного сечения. В итоге получаем четырехугольник КВ’С’D’ — искомое сечение.

1. Нахождение площади сечения в многогранниках.

2. Использование свойств подобных треугольников.

3. Нахождение расстояния и угла между скрещивающимися прямыми в многограннике.

4. Угол между плоскостями.

5. Сечения

6. Отношение объемов частей многогранника.

7. Проекции и сечения правильных многогранников.

Нахождение площади сечения в многогранниках.

айти площадь фигуры в сечении куба ABCDA’B’C’D’ с ребром «а» плоскостью, проходящей через вершину D и точки E и F на ребрах A’D’ и C’D’ соответственно, если A’E=k*D’E и C’F=k*D’F.

айти площадь фигуры в сечении куба ABCDA’B’C’D’ с ребром «а» плоскостью, проходящей через вершины C’ и D и точку E на ребре A’D’, если A’E=k*D’E.

айти площадь фигуры в сечении куба ABCDA’B’C’D’ с ребром «а» плоскостью, проходящей через вершину D и точки E и F на ребрах A’D’ и C’D’ соответственно, если D’E=k*A’E и C’F=k*D’F.

айти площадь фигуры в сечении куба ABCDA’B’C’D’ с ребром «а» плоскостью, проходящей через вершины A’ и C’ и точку F на ребре AD, если AF=k*DF.

айти площадь фигуры в сечении правильной четырехугольной пирамиды ABCDM с ребрами «а» (половинка октаэдра) плоскость, проходящей через сторону основания AD и точку E на боковом ребре MC, если CE=k*ME.

айти площадь фигуры в сечении правильного тетраэдра ABCM с ребром «а» плоскостью, проходящей через точки D, E и F на ребрах MA, MB и BC соответственно, если MD:AD=ME:BE=BF:CF=k.

айти площадь фигуры в сечении правильной треугольной призмы ABCA’B’C’ плоскостью, проходящей через сторону основания A’B’ и точку D на стороне BC другого основания, если CD=k*BD, сторона основания призмы равна «a» и высота H=n*a.

айти площадь фигуры в сечении куба ABCDA’B’C’D’ с ребром «а» плоскостью, проходящей через вершину C’ и середины ребер A’D’ и CD.

Использование свойств подобных треугольников.

о многих задачах использование свойств подобных треугольников, как правило, не является основным фактором процесса решения, — что и наблюдалось в некоторых задача темы №1.

Поэтому далее представлены несколько простейших задач, в которых подобные треугольники играют главную роль, — тем более, что их нужно еще и построить (и увидеть. ) с помощью стандартного стереометрического приема: одну плоскость пересечь другой плоскостью и построить их линию пересечения по двум общим для плоскостей точкам.

каком отношении диагональ A’C делится плоскостью, проходящей в кубе ABCDA’B’C’D’ через вершины B и D’ и 1) вершину А, 2) середину ребра AD?

каком отношении диагональ BD’ делится плоскостью, проходящей в кубе ABCDA’B’C’D’ через середины ребер AD и CD и точку F на ребре BB’, если B’F=k*BF?

остроить сечение куба ABCDA’B’C’D’ плоскостью, проходящей через вершины B’ и D’ и середину ребра AD. В каком отношении эта плоскость делит отрезок, соединяющий вершину A’ с точкой F на ребре CC’ , если C’F=k*CF?

остроить сечение правильной треугольной пирамиды ABCM плоскостью, проходящей через сторону основания АС и точку F на боковом ребре МВ при условии, что BF=k*MF. В каком отношении эта плоскость делит высоту пирамиды МО?

остроить сечение правильной четырехугольной пирамиды ABCDM плоскостью, проходящей через сторону основания AD и точку F на боковом ребре MC, если CF=k*MF. В каком отношении эта плоскость делит высоту пирамиды МО?

Нахождение расстояния и угла между скрещивающимися прямыми в многограннике.

Для нахождения расстояния между скрещивающимися прямыми можно воспользоваться четырьмя основными способами:

1)Нахождение длины общего перпендикуляра двух скрещивающихся прямых, то есть отрезка с концами на этих прямых и перпендикулярного обеим.

2)Нахождение расстояния от одной из скрещивающихся прямых до параллельной ей плоскости, проходящей через другую прямую.

3)Нахождение расстояния между двумя параллельными плоскостями, проходящими через заданные скрещивающиеся прямые.

4)Нахождение расстояния от точки, — являющейся проекцией одной из скрещивающихся прямых на перпендикулярную ей плоскость, — до проекции другой прямой на ту же самую плоскость.

кубе с ребром «a» найти расстояние и угол между любым ребром и диагональю, не пересекающей его грани.

кубе с ребром «а» найти расстояние и угол между непересекающимися диагоналями двух смежных граней. (использовать несколько способов)

Представьте 4 варианта решения данной задачи и выберите самый рациональный из них. Обоснуйте свой выбор.

кубе ABCDA’B’C’D’ с ребром «а» найти расстояние и угол между прямыми АС и B’F при F принадлежащей DD’ и DF=k*D’F.

правильной шестиугольной призме ABCDEFA’B’C’D’E’F’ с высотой «Н» и стороной основания «а». Найти расстояние и угол между прямыми: 1).AA’ и D’E; 2). AF и BE’.

правильной шестиугольной призме ABCDEFA’B’C’D’E’F’ со стороной основания «а» и высотой Н=k*a. Найти расстояние и угол между прямыми BE’ и DF.

Нахождение расстояния и угла между скрещивающимися прямыми в многограннике.

кубе ABCDA’B’C’D’ определить угол между плоскостями сечений AB’C’D и CB’A’D.

правильной четырехугольной призме ABCDA’B’C’D’ со стороной основания «а» и высотой Н=k*a определить угол, образованный плоскостями сечений, проходящих соответственно через вершины B’,D и середину ребра СС’ и через вершины C’, А и середину ребра DD’.

правильной треугольной пирамиде, у которой высота в «k» раз больше стороны основания, определить угол, образованный плоскостью,

проходящей через боковое ребро и пересекающуюся с ним медиану основания, и плоскостью, проходящей через ту же медиану и середину любого другого бокового ребра.

Сечения.

пространстве даны две параллельные плоскости и две сферы, причем первая сфера касается первой плоскости в точке А, вторая сфера касается второй плоскости в точке В и сферы касаются друг друга в точке С. Докажите, что точки А, В и С лежат на одной прямой.

коло шара описан усеченный конус, основания которого являются большими кругами двух других шаров. Определите площадь полной поверхности усеченного конуса, если сумма площадей поверхностей трех шаров равна 8.

Два противоположных ребра тетраэдра перпендикулярны, а их длины равны а и b расстояние — между ними равно с. В тетраэдр вписан куб, четыре ребра которого перпендикулярны этим двум ребрам тетраэдра, а на каждой грани тетраэдра лежат ровно две вершины куба. Найдите ребро куба.

акие правильные многоугольники могут получиться при пересечении куба плоскостью?

се сечения некоторого тела плоскостями являются кругами. Докажите, что это тело — шар.

ерез вершину А прямого кругового конуса проведено сечение максимальной площади. Его площадь и два раза больше площади сечения, проходящего через ось конуса. Найдите угол при вершине осевого сечения конуса.

лоскость делит медианы граней АВС, АСD и АDВ тетраэдра АВСD, выходящие из вершины Л, в отношениях 2:1, 1:2 и 4:1, считая от вершины. Пусть Р, Q и R. — точки пересечения этой плоскости с прямыми АВ, АС и АD. Найдите отношения АР : РВ, АQ: QС и АR : RD.

правильной шестиугольной пирамиде SАВСDЕF (с вершиной S> на диагонали АD взяты три точки, делящие ее на 4 равные части. Через эти точки проведены сечения, параллельные плоскости SАВ. Найдите отношения площадей полученных сечений.

ечение правильной четырехугольной пирамиды является правильным пятиугольником. Докажите, что боковые грани этой пирамиды — правильные треугольники.

Отношение объемов частей многогранника.

айти отношение объемов частей куба ABCDA’B’C’D’ с ребром «а», полученных разбиением его сечением плоскостью, проходящей через вершину D и точки E и F на ребрах A’D’ и C’D’ соответственно, если A’E=k*D’E и C’F=k*D’F.

айти отношение объемов частей куба ABCDA’B’C’D’ с ребром «а» полученных разбиением его сечением плоскостью, проходящей через вершины C’ и D и точку E на ребре A’D’, если A’E=k*D’E.

айти отношение объемов частей куба ABCDA’B’C’D’ с ребром «а»полученных разбиением его сечением плоскостью, проходящей через вершины A’ и C’ и точку F на ребре AD, если AF=k*DF.

айти отношение объемов частей правильной треугольной призмы ABCA’B’C’полученных разбиением её сечением плоскостью, проходящей через сторону основания A’B’ и точку D на стороне BC другого основания, если CD=k*BD, сторона основания призмы равна «a» и высота H=n*a.

Проекции и сечения правильных многогранников.

окажите, что проекции додекаэдра и икосаэдра на плоскости, параллельные их граням, являются правильными многоугольниками.

окажите, что проекция додекаэдра на плоскость, перпендикулярную прямой, проходящей через его центр и середину ребра, является шестиугольником (а не десятиугольником).

а) окажите, что проекция икосаэдра на плоскость. перпендикулярную прямой, проходящей через его центр и вершину, является правильным 10-угольником. б). Докажите, что проекция додекаэдра на плоскость, перпендикулярную прямой, проходящей через его центр и вершину, является неправильным 12- угольником.

уществует ли сечение куба, являющееся правильным т шетиугольником?

уществует ли сечение октаэдра, являющееся правильным шестиугольником?

уществует ли сечение додекаэдра, являющееся правильным шестиугольником?

ве грани АВС и АВD икосаэдра имеют общее ребро АВ. Через вершину D проводится плоскость, параллельная плоскости АВС. Верно ли, что сечение икосаэдра этой плоскостью является правильным шестиугольником?

Ответы к задачам по темам:

1. Нахождение площади сечения в многогранниках.

2. Использование свойств подобных треугольников.

3. Нахождение расстояния и угла между скрещивающимися прямыми в многограннике.

4. Угол между плоскостями.

5. Сечения

6. Отношение объемов частей многогранника.

7. Проекции и сечения правильных многогранников.

1. Нахождение площади сечения в многогранниках.

№1 №2 №3 №4 №5 №6 №7 №8

2. Использование свойств подобных треугольников.

1-ый случай

2-ой случай

4. Угол между плоскостями.

Точка С принадлежит плоскости CB’A’D (так как CD’ перпендикулярна C’D как диагонали квадрата и так как B’C’ перпендикулярна плоскости CC’D’D, — из чего следует B’C’ перпендикулярна СЕ, — то получаем СЕ перпендикулярна B’C’ и СЕ перпендикулярна C’D). Затем проводим EF перпендикулярно B’D и тогда получаем B’D перпендикулярна CF (по теореме о трех перпендикулярах: CF по отношению к плоскости AB’C’D является наклонной, СЕ — перпендикуляром и EF — проекцией наклонной CF; то она перпендикулярна и самой наклонной CF). Так как EF и CF принадлежат соответственно обеим плоскостям, то угол фи (угол CFE) является искомым.

После этого обоснования следует несложная вычислительная часть.

Нетрудно обосновать, что в сечениях — ромбы, половинки которых (см. рисунок) расположены в пространстве одинаково относительно линии пересечения плоскостей FE (фигуры A»B’EF и D»C’EF), в результате чего перпендикуляры A»M и D»M, проведенные в обеих фигурах к их линии пересечения, попадут в одну точку М, причем — внутри, а не снаружи призмы, так как углы B’A»D и C’D»A — тупые (B’D и больше BD=AC=A»C» и C’A больше AC=BD=B»D»). Далее, найдя диагонали и стороны ромбов, можно найти отрезки A»M и D»M с помощью, например, двух формул для площади ромба Примечание: Безусловно, в этой и аналогичных задачах никакие размеры многогранника (например, «a») не нужны, поэтому при подборе численных значений параметра «k» для различных вариантов задачи содержание ее условия в соответствующем месте должно формулироваться, например, так: «. в призме, у которой высота во столько-то раз больше стороны основания. «, и т. д.

3. Нахождение расстояния и угла между скрещивающимися прямыми в многограннике.

Данная задача в качестве классического образца рассматривается в некоторых пособиях, — но, как правило, ее решение дается способом проектирования на некоторую плоскость. Рассмотрим 4 способа решения данной задачи.

№1 Решение задачи первым способом предполагает:
— непростое обоснование того, что искомый перпендикуляр (h скр.) с концами на двух данных скрещивающихся прямых располагается внутри куба (а не вне его);
— ориентировочное определение местоположения этого перпендикуляра;
— догадку о том, что для нахождения длины отрезка h скр. необходимо с помощью теоремы о трех перпендикулярах спроектировать его на смежные грани куба, которым принадлежат скрещивающиеся прямые ( диагонали) а уже затем подойти к несложному решению:

2. Решение задачи вторым способом предполагает следующие действия:
— построение в кубе секущей плоскости, параллельной одной из прямых A’C’; так как АС параллельна A’C’, то A’C’ параллельна плоскости ACD’ по признаку параллельности прямой плоскости;
— отыскание внутри куба прямой, перпендикулярной секущей плоскости; здесь требуется догадка и обоснование того, что такой прямой является главная диагональB’D ( АС перпендикулярна ВД и, так как ВД является проекцией наклонной В’D на плоскость основания АВСД, то по теореме о трех перпендикулярах получаем АС перпендикулярна В’D ; аналогично устанавливается, что CD’ перпендикулярна B’D и, так как получили перпендикулярность главной диагонали В’D двум непараллельным прямым АС и СD’ , принадлежащим плоскости сечения АСD’ , то по признаку перпендикулярности прямой и плоскости :B’D перпендикулярна плоскости ACD’);

-построение еще одной секущей плоскости, проходящей через диагональ В’D и пересекающей вторую из скрещивающихся прямых A’C’; этой плоскостью удобно выбрать диагональное сечение BB’D’D этому признаку перпендикулярности двух плоскостей плоскости BB’D’D перпендикулярна плоскости ACD’, так как плоскость BB’D’D проходит через прямую (B’D), перпендикулярную другой плоскости (ACD’). Далее строиться линия пересечения обоих плоскостей по 2 их общим точкам (D’O) и фиксируется пересечением этой линии диагональю B’D (точка N);
-и наконец, по теореме о том, что если плоскость перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой, из точки O’ принадлежит A’C’ проводим в плоскости сечения BB’D’D до пересечения с D’O отрезок O’M параллелен B’D; при этом будет O»M перпендикулярен плоскости ACD’ и потому O’M = h скр.;
— затем в вычислительной части решения, рассмотрев сечение BB’D’D и в нем — прямоугольный треугольник OO’D’, находим: Как видим, оба первых способа малопригодны для задач, представляющих хотя бы какую-то сложность

3. Решение задачи третьим способом предполагает:
— построение параллельных двух секущих плоскостей, содержащих две заданные скрещивающиеся прямые, — с помощью пересекающихся пар соответственно параллельных прямых (BC’ параллельна AD’ u AC параллельна A’C’ => плоскость A’BC’ параллельна плоскости ACD’)
— отыскание и построение прямой, перпендикулярной одной из двух построенных секущих плоскостей ( главная диагональ B’D перпендикулярна плоскости ACD’ — доказательство приведено в предыдущем способе решения зада
— отыскание и построение точек пересечения указанной прямой (В’D) с обеими секущими параллельными плоскостями,- для чего необходимо построение любой третьей секущей плоскости( в данном случае, например, BB’D’D) содержащей указанную прямую(B’D), а затем — построение линий пересечения третьей секущей плоскости с первыми двумя (BO’ u D’O); зафиксированные таким образом точки М и N т определяют отрезок МN=h скр.

-и, наконец, в вычислительной части решения можно воспользоваться приемом из предыдущего способа решения или же прибегнуть к подобию треугольников:

4.Решение задачи четвертым способом предполагает:
-отыскание и построение такой секущей плоскости( в данном случае — BB’D’D), которая перпендикулярна одной из скрещивающихся прямых ( A’C’ перпендикулярен BB’D’D — так как A’C’ перпендикулярен B’D’ и DD’ перпендикулярен плоскости A’B’C’D’ => DD’ перпендикулярен A’C’, т. е. A’C’ перпендикулярна двум непараллельным прямым, принадлежащим секущей плоскости) и на которую указанная прямая (A’C’) проектируется в точку (O’); причем при выборе секущей плоскости желательно, чтобы хотя бы один из концов отрезка второй прямой принадлежал этой секущей плоскости;
— построение проекции второй прямой на эту секущую плоскость, — для чего из концов отрезка этой прямой (в данном случае из точки А ) перпендикуляры на эту плоскость ( в данном случае АО) проводятся параллельно первой из скрещивающихся прямых (АО параллельна A’C’);
— после построения проекции D’O к ней в плоскости сечения BB’D’D проводится перпендикуляр O’M из первоначально полученной точки O’ — проекции первой прямой на ту же секущую плоскость; получаем O’M = h скр.;
— и, наконец, в вычислительной части решения можно воспользоваться уже известным приемом нахождения высоты к гипотенузе прямоугольного треугольника (OO’D’):h скр

В данной задаче для выбора способа решения определяющим является перпендикулярность прямой АС диагональной плоскости ВB’D’D (т. к. АС перпендикулярна ВD и АС перпендикулярна BB’), которой принадлежит другая прямая B’F, т. е. секущая плоскость BB’D’D удобна для выбора ее в качестве плоскости проекции. А далее следует несложная вычислительная часть:
1). Иэ подобия треугольника DFT и треугольника D’FB’ находим DT = kd;
2). Из подобия треугольника NOT и треугольника BB’T находим ON:

Данная задача представлена здесь для демонстрации применения второго способа (построение перпендикуляра от первой прямой к параллельной плоскости, содержащей вторую прямую) к простейшим ситуациям расположения скрещивающихся прямых в таком непростом многограннике, каким является правильная шестиугольная призма.

5. Сечения.

По всяком случае, точки А, В и С лежат в одной плоскости, и поэтому можно рассмотреть сечение плоскостью, содержащей эти точки. Так как плоскость сечения проходит через точку касания сфер (сферы плоскости), и сечении получаются касающиеся окружности (окружность и прямая). Пусть О’ и 0» — центры первой и второй окружностей. Так как О’А || 0»В и точки O’, С и 0» лежат па одной прямой, угол АО’С = углу ВО»С. Поэтому угол АСО’ = углу ВСО», т. е. точки А, В и С лежат на одной прямой.

Осевое сечение данного усеченного конуса является описанной трапецией АВСD с основаниями АD = 2R и ВС = = 2r. Пусть Р — точка касания вписанной окружности со стороной АВ, О — центр вписанной окружности. В треугольнике АВО сумма углов при вершинах А и В равна 90°, поэтому он прямоугольный. Следовательно, АР : РО — РО : ВР, т. е. РО’2 = АР*ВР. Ясно также, что АР = R и ВР = r. Поэтому радиус РО вписанной в конус сферы равен квадратному корню из произведения R и r, а значит, S = 4п(R2 + Rr+ r2). Выражая объем данного усеченного конуса по формулам, получаем, что площадь его полной поверхности равна 2п(R2 + Rr+ r2) = S/2 (нужно учесть, что высота усеченного конуса равна удвоенному радиусу сферы, около которой он описан).

Общий перпендикуляр к данным ребрам делится параллельными им плоскостями граней куба на отрезки длиной у, х и г (х — длина ребра куба; отрезок длиной у прилегает к ребру а). Плоскости граней куба, параллельные данным ребрам, пересекают тетраэдр по двум прямоугольникам. Меньшие стороны этих прямоугольников равны ребру куба х. Так как стороны этих прямоугольников легко вычисляются, получаем х = bу/с и х = az/с. Следовательно, с=х+у+г=х+сх/b + еx/а, т. е. х=аЬс/(аb + bс + сa).

Каждая сторона полученного многоугольника принадлежит одной из граней куба, поэтому число его сторон не превосходит 6. Кроме того, стороны, принадлежащие противоположным граням куба, параллельны, так как линии пересечения плоскости с двумя параллельными плоскостями параллельны. Следовательно, сечение куба не может быть правильным пятиугольником, так как у того нет параллельных сторон. Легко проверить, что правильный треугольник, квадрат и правильный шестиугольник могут быть сечениями куба.

Рассмотрим некоторый круг, являющийся сечением данного тела, и проведем через его центр прямую l, перпендикулярную его плоскости. Эта прямая пересекает данное тело по некоторому отрезку АВ. Все сечения, проходящие через прямую l являются кругами с диаметром АВ.

Рассмотрим произвольное сечение, проходящее через вершину А. Это сечение является треугольником АВС, причем его стороны АВ и АС являются образующими конуса, т. с. имеют постоянную длину. Поэтому площадь сечения пропорциональна синусу угла ВАС. Угол ВАС изменяется от 0° до ф,