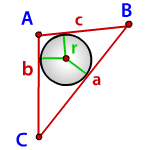
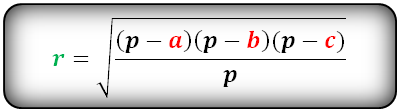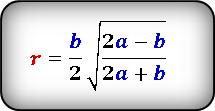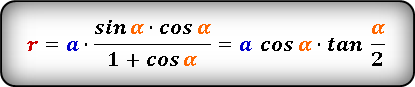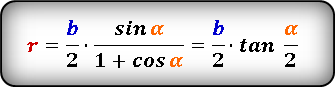Если окружность располагается внутри угла и касается его сторон, её называют вписанной в этот угол. Центр такой вписанной окружности располагается на биссектрисе этого угла.
Если же она лежит внутри выпуклого многоугольника и соприкасается со всеми его сторонами, она называется вписанной в выпуклый многоугольник.
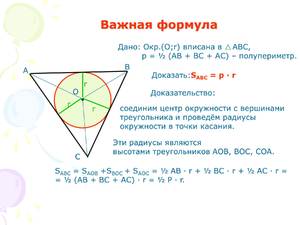
- Окружность, вписанная в треугольник
- Вычисление с помощью полупериметра
- Вычисление с учётом площади треугольника
- Расчёт с помощью тригонометрических функций
- Окружность, вписанная в прямоугольный треугольник
- Видео
- Все формулы для радиуса вписанной окружности
- Радиус вписанной окружности в треугольник
- Радиус вписанной окружности в равносторонний треугольник
- Радиус вписанной окружности равнобедренный треугольник
- Нахождение радиуса вписанной в треугольник окружности
- Формулы вычисления радиуса вписанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
- Примеры задач
- Видео
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Окружность, вписанная в треугольник
Окружность, вписанная в треугольник, соприкасается с каждой стороной этой фигуры лишь в одной точке. В один треугольник возможно вписать лишь одну окружность.
Радиус такой окружности будет зависеть от следующих параметров треугольника:
- Длин сторон треугольника.
- Его площади.
- Его периметра.
- Величины углов треугольника.
Для того чтобы вычислить радиус вписанной окружности в треугольник, не всегда обязательно знать все перечисленные выше параметры, поскольку они взаимосвязаны между собой через тригонометрические функции.
Вычисление с помощью полупериметра
Чтобы рассчитать величину радиуса вписанной окружности в треугольник, необходимо учитывать следующие параметры:
- Если известны длины всех сторон геометрической фигуры (обозначим их буквами a, b и c), то вычислять радиус придётся путём извлечения квадратного корня.
- Приступая к вычислениям, необходимо добавить к исходным данным ещё одну переменную — полупериметр (р). Его можно рассчитать, сложив все длины и полученную сумму разделив на 2. p = (a+b+c)/2. Таким образом можно существенно упростить формулу нахождения радиуса.
- В целом формула должна включать в себя знак радикала, под который помещается дробь, знаменателем этой дроби будет величина полупериметра р.
- Числителем данной дроби будет представлять собой произведение разностей (p-a)*(p-b)*(p-c)
- Таким образом, полный вид формулы будет представлен следующим образом: r = √(p-a)*(p-b)*(p-c)/p).
Вычисление с учётом площади треугольника
Если нам известна площадь треугольника и длины всех его сторон, это позволит найти радиус интересующей нас окружности, не прибегая к извлечению корней.
- Для начала нужно удвоить величину площади.
- Результат делится на сумму длин всех сторон. Тогда формула будет выглядеть следующим образом: r = 2*S/(a+b+c).
- Если воспользоваться величиной полупериметра, можно получить совсем простую формулу: r = S/p.
Расчёт с помощью тригонометрических функций
Если в условии задачи присутствует длина одной из сторон, величина противоположного угла и периметр, можно воспользоваться тригонометрической функцией — тангенсом. В этом случае формула расчёта будет иметь следующий вид:
r = (P /2- a)* tg (α/2), где r — искомый радиус, Р — периметр, а — значение длины одной из сторон, α — величина противоположного стороне, а угла.
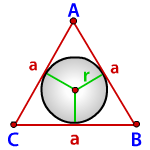
Радиус окружности, которую необходимо будет вписывать в правильный треугольник, можно найти по формуле r = a*√3/6.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

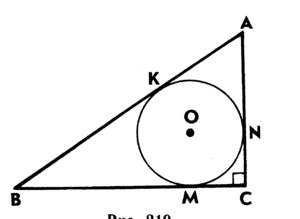
Окружность, вписанная в прямоугольный треугольник
В прямоугольный треугольник можно вписать только одну окружность. Центр такой окружности одновременно служит точкой пересечения всех биссектрис. Эта геометрическая фигура имеет некоторые отличительные черты, которые необходимо учесть, вычисляя радиус вписанной окружности.
- Для начала необходимо выстроить прямоугольный треугольник с заданными параметрами. Построить такую фигуру можно по размеру её одной стороны и величинам двух углов или же по двум сторонам и углу между этими сторонами. Все эти параметры должны быть указаны в условии задачи. Треугольник обозначается как АВС, причём С — это вершина прямого угла. Катеты при этом обозначаются переменными, а и b, а гипотенуза — переменной с.
- Для построения классической формулы и вычисления радиуса окружности необходимо найти размеры всех сторон описанной в условии задачи фигуры и по ним вычислить полупериметр. Если в условиях даются размеры двух катетов, по ним можно вычислить величину гипотенузы, исходя из теоремы Пифагора.
- Если в условии дан размер одного катета и одного угла, необходимо понять, прилежащий этот угол или противолежащий. В первом случае гипотенуза находится с помощью теоремы синусов: с=a/sinСАВ, во втором случае применяют теорему косинусов с=a/cosCBA.
- Когда все расчёты выполнены и величины всех сторон известны, находят полупериметр по формуле, описанной выше.
- Зная величину полупериметра, можно найти радиус. Формула представляет собой дробь. Её числителем является произведение разностей полупериметра и каждой из сторон, а знаменателем —величина полупериметра.
Следует заметить, что числитель данной формулы является показателем площади. В этом случае формула нахождения радиуса гораздо упрощается — достаточно разделить площадь на полупериметр.
Определить площадь геометрической фигуры можно и в том случае, если известны оба катета. По сумме квадратов этих катетов находится гипотенуза, далее вычисляется полупериметр. Вычислить площадь можно, умножив друг на друга величины катетов и разделив полученное на 2.
Если в условиях даны длины и катетов и гипотенузы, определить радиус можно по очень простой формуле: для этого складываются длины катетов, из полученного числа вычитается длина гипотенузы. Результат необходимо разделить пополам.
Видео:Радиус вписанной окружности, формулу через площадь и полупериметрСкачать

Видео
Из этого видео вы узнаете, как находить радиус вписанной в треугольник окружности.
Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Все формулы для радиуса вписанной окружности
Видео:Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

Радиус вписанной окружности в треугольник
a , b , c — стороны треугольника
p — полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
Видео:Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

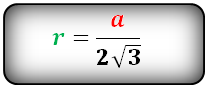
Радиус вписанной окружности в равносторонний треугольник
a — сторона треугольника
r — радиус вписанной окружности
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
Видео:112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

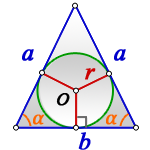
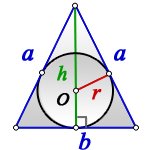
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
α — угол при основании
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Нахождение радиуса вписанной в треугольник окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в произвольный (любой), прямоугольный, равнобедренный или равносторонний треугольник. Также разберем примеры решения задач для закрепления представленного теоретического материала.
Видео:Геометрия Периметр треугольника равен 32 см а радиус вписанной окружности 1,5 см Найдите площадьСкачать

Формулы вычисления радиуса вписанной окружности
Произвольный треугольник
Радиус окружности, вписанной в любой треугольник, равняется удвоенной площади треугольника, деленной на его периметр.
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, вписанной в прямоугольный треугольник, равняется дроби, в числителе которого сумма катетов минус гипотенуза, в знаменателе – число 2.
где a и b – катеты, c – гипотенуза треугольника.
Равнобедренный треугольник
Радиус вписанной в равнобедренный треугольник окружности вычисляется по формуле ниже:
где a – боковые стороны, b – основание треугольника.
Равносторонний треугольник
Радиус вписанной в правильный (равносторонний) треугольник окружности рассчитывается следующим образом:
где a – сторона треугольника.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Примеры задач
Задание 1
Дан треугольник со сторонами 5, 7 и 10 см. Вычислите радиус вписанной в него окружности.
Решение
Сперва вычислим площадь треугольника. Для этого применим формулу Герона:
Остается только применить соответствующую формулу для вычисления радиуса круга:
Задание 2
Боковые стороны равнобедренного треугольника равны 16 см, а основание 7 см. Найдите радиус вписанной в фигуру окружности.
Решение
Воспользуемся подходящей формулой, подставив в нее известные значения:
📹 Видео
Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Площадь многоугольника через радиус вписанной окружностиСкачать

Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Формула радиуса вписанной окружности треугольника. Геометрия 9 классСкачать

Формулы площади треугольника. Вписаная и описаная окружностьСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

РАДИУС вписанной окружности #математика #огэ #огэматематика #данирСкачать

Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Площадь треугольника через периметр и радиусСкачать