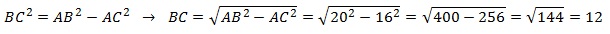Найдите х у о центр окружности 12 заданий с решением

Вопрос по геометрии:

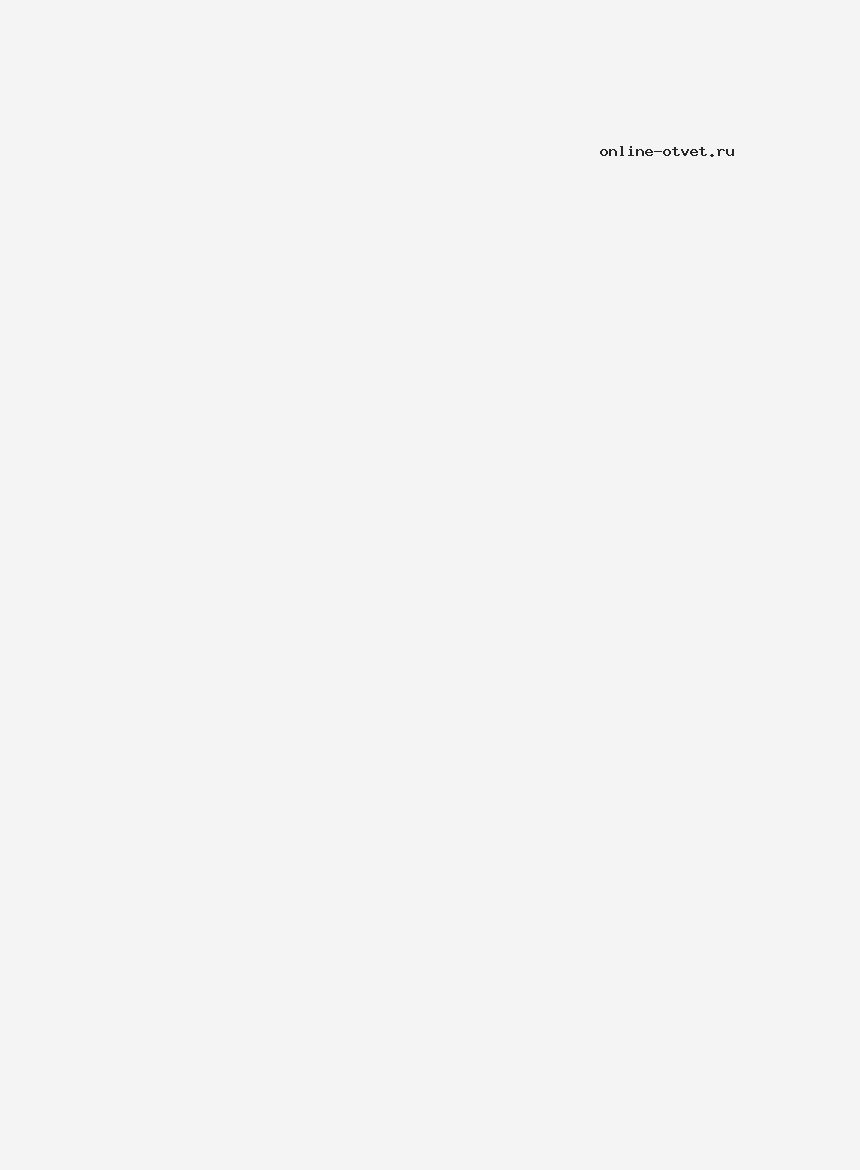
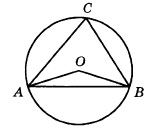
Найти x , y (о- центр окружности)

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Найти центр и радиус окружностиСкачать

Найти х, у ( О центр окружности)?

Геометрия | 5 — 9 классы

Найти х, у ( О центр окружности).

Чтобы можно было описать окружность около четырехугольника, нужно чтобы было так : х + 110 = 180

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Длина хорды окружности равна 120, а расстояние от центра окружности до этой хорды равно 45?

Длина хорды окружности равна 120, а расстояние от центра окружности до этой хорды равно 45.

Найти диаметр окружности.

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

В окружности, на расстоянии 21см от ее центра, проведена хорда длиной 40см?

В окружности, на расстоянии 21см от ее центра, проведена хорда длиной 40см.

Найти радиус окружности.

Видео:ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

Длина хорды окружности равна 120а расстояние от центра окружности до этой хорды раано 32?

Длина хорды окружности равна 120а расстояние от центра окружности до этой хорды раано 32.

Найти диаметр окружности.

Видео:Уравнение окружности (1)Скачать

Точка О — центр окружностим, угол аов = 128 найти асв?

Точка О — центр окружностим, угол аов = 128 найти асв.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Найти радиус окружности если хорда длиной 24см удалена от центра окружности на 5см?

Найти радиус окружности если хорда длиной 24см удалена от центра окружности на 5см.

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Длина хорды окружности равна 30, а расстояние от центра окружности до этой хорды 36?

Длина хорды окружности равна 30, а расстояние от центра окружности до этой хорды 36.

Найти диаметр окружности.

Видео:ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать

Дана окружность, в ней проведена хорда 42?

Дана окружность, в ней проведена хорда 42.

Из центра О в центр хорды падает высота 72.

Найти диаметр окружности.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

О — центр окружности В — точка касания Найти : угол АВD?

О — центр окружности В — точка касания Найти : угол АВD.

Видео:Точка O – центр окружности, ∠BOC=160° ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Треугольник ABC вписан в окружность?

Треугольник ABC вписан в окружность.

Найти радиус окружности, если AB = 24см, а центр окружности удален от AB на 5см.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Радиус окружности = 10, хорда = 12, найти расстояние от центра окружности до хорды?

Радиус окружности = 10, хорда = 12, найти расстояние от центра окружности до хорды.

На этой странице сайта размещен вопрос Найти х, у ( О центр окружности)? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 — 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

Данная величина есть площадь под графиком функции на отрезке [ — 1, 2], что по определению равно : Ответ : 12.

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник⇒ AB = BF = FE = EC Противоположные стороны равны. Пусть АВ = х, тогда : (х + 3х) * 2 = 88 4х = 88 / 2 4х = 44 х = 44 / 4 х = 11 см Ответ : АВ = 11 см.

Т. к. Против большего угла, лежит большая сторона, то первой будет сторона AC, второй по величине угол BCA (70°) следовательно дальше сторона BA, а потом сторона BC, т. К против неё наименьший угол BAC. AC — BA — BC.

Так как угол 1 = углу 2, то АОС — равнобедренный, = > АО = ОС Треугольники АОВ и СОВ равны по двум сторонам и углу между ними(ВО — общая ; АО = СО ; Угол 3 = Углу 4) Из этого следует, что АВ = ВС, следовательно АВС — равнобедренный.

Давление уменьшилось в 2 раза.

30 : 5 = 6 см отрезок МЕ. Так значит ДМ = 24 см.

Скрещивающиеся прямые не имеют общих точек. У прямых AD и AB — общая точка A. У прямых AD и BD — общая точка D. У прямых AD и CD — общая точка D. ПрямыеAD и BC — скрещивающиеся.

BD — медиана и высота значит треугольник ABC равнобедренный, AB = BC, AD = DC, AB + AD = PABD — BD = 15 — 4 = 11 см PABC = 2 * (AB + AD) = 11 * 2 = 22 см периметр треугольника ABC = 22 cм.

ВС = АВ + АС Х = 6 + 9 = 15 ВС = 15.

Т. к точка А делит отрезок ВС на два отрезка, то этот отрезок ВС равен сумме двух получившихся отрезков, т. Е ВС = АВ + АС = 6 + 9 = 15. Ответ : отрезок ВС равен 15 сантиметрах.

Видео:№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

Задание №17 ОГЭ по математике

Видео:Быстро и легко определяем центр любой окружностиСкачать

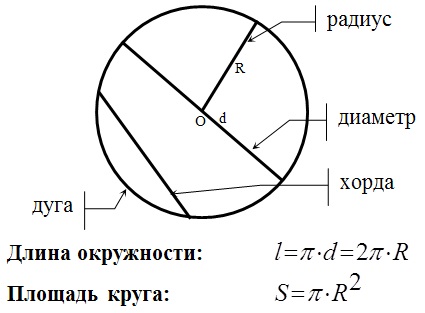
Окружность, круг и их элементы

В 17 задании ОГЭ по математике необходимо решить простую задачу по геометрии. Для успешного решения необходимо обладать базовыми знаниями по геометрии вообще, так как сложно выделить какую-то одну тему, по которой даны задания. Это относится ко всему модулю геометрии. Я рекомендую повторить понятия центральные и вписанные углы, свойства касательных к окружности, взаимосвязь между радиусом описанной или вписанной окружности в геометрические фигуры — в первую очередь прямоугольный треугольник и квадрат.

По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.

Ответом в задании 17 является целое число или конечная десятичная дробь.

Теория к заданию №17

Несмотря на то, что в задании №17 могут потребоваться любые знания по геометрии, в данном разделе мы разберем теорию по теме «окружность».

Начнем рассмотрение с понятия вписанная окружность:

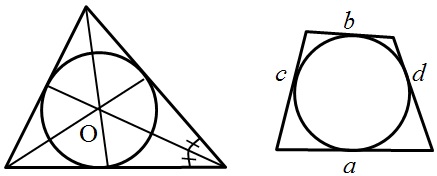
1. Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
2. Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой: a + b = c + d

Длинна окружности и площадь:

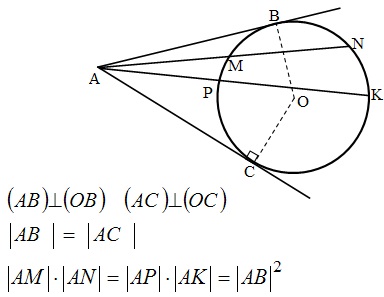
Касательная и секущая:

• Касательная – прямая, имеющая с окружностью одну общую точку.
• Секущая – прямая, имеющая с окружностью две общие точки.

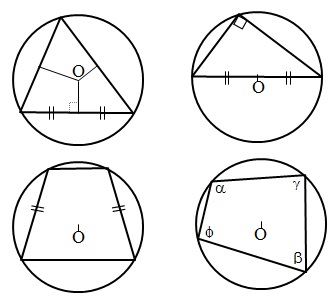
Описанная окружность и её свойства:

1. Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трем сторонам.
2. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
3. Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.
4. Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой.

Хорда – отрезок, соединяющий две точки окружности.

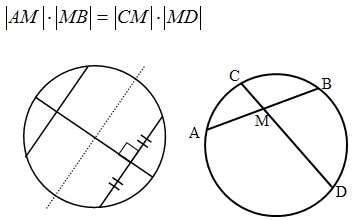
• Диаметр, делящий хорду пополам, перпендикулярен хорде.
• В окружности равные хорды равноудалены от центра окружности.
• Отрезки пересекающихся хорд связаны равенством:

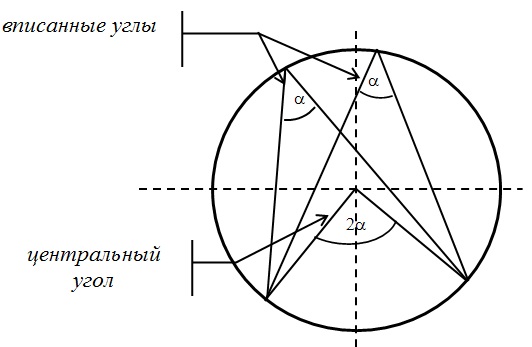
Центральный и вписанный углы:

Ниже я разобрал три различных примера 10 задания. Если у вас остались пожелания, или вы хотите разобрать задачу, которой здесь нет, напишите об этом в комментарии.

Разбор типовых вариантов заданий №17 ОГЭ по математике

Первый вариант задания

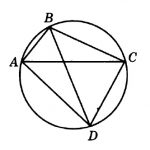
Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.

Решение:

Внимательно посмотрим на рисунок. Угол ABC опирается на дугу ADC, а угол CAD — на дугу DC. Угол, который нам необходимо найти — ABD, опирается на дугу AD — которая является частью дуги ADC за вычетом дуги DC. Значит, угол ABD равен разности углов ABC и CAD:

∠ABD = 92 — 60 = 32

Второй вариант задания

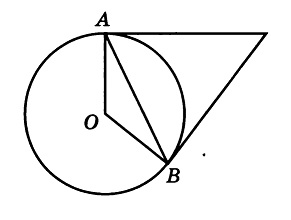
Касательные в точках A и B к окружности с центром O пересекаются под углом 2º. Найдите угол ABO. Ответ дайте в градусах.

Решение:

Во-первых, касательные равны между собой по длине, а значит треугольник с основанием AB равнобедренный. Угол при вершине этого треугольника равен 2 градуса по условию, значит углы при основании равны:

Во-вторых, касательные перпендикулярны радиусу, то есть угол между ними и радиусом равен 90 градусов.

Заметим, что угол ABO, который необходимо найти, является частью угла между касательной и радиусом, а именно за вычетом угла, который мы нашли в первом пункте. Значит, этот угол равен:

Третий вариант задания

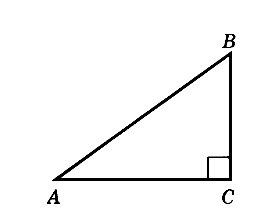
В треугольнике ABC известно, что AC = 16, BC = 12, угол C равен 90º. Найдите радиус описанной около этого треугольника окружности.

Решение:

Для решения необходимо вспомнить, что центр описанной около прямоугольного треугольника окружности расположен в середине гипотенузы. То есть гипотенуза является диаметром, а её половина — радиусом.

По теореме Пифагора найдем гипотенузу AB:

AB² = BC² + AC² = 12² + 16² = 144 + 256 = 400

Гипотенуза равна 20, значит радиус — 10.

Демонстрационный вариант ОГЭ 2019

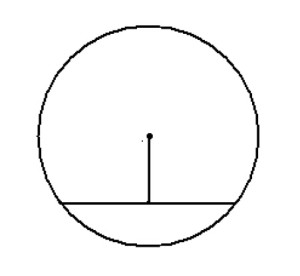
Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см.

Решение:

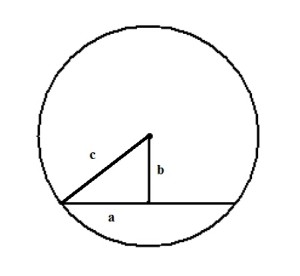
Для решения данной задачи необходимо провести радиус окружности к точке начала хорды:

Получаем прямоугольный треугольник, где гипотенуза c — радиус и равна 13 см, b — расстояние до хорды — 5 см. По теореме Пифагора находим катет a:

a² = c² — b² = 13² — 5² = 169 — 25 = 144

Но а — лишь половина хорды, поэтому вся хорда равна 2 • а = 24

Четвертый вариант задания

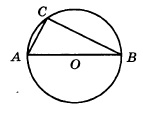
Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 10. Найдите ВС, если АС=16.

Решение:

Сторона АВ треуг-ка АСВ является диаметром окружности. Это означает, что угол АСВ опирается на диаметр. Тогда угол АСВ равен 90 0 , и, следовательно, ∆АСВ прямоугольный.

Если ∆АСВ прямоугольный, то для нахождения одной из его сторон можно применить т.Пифагора. По т.Пифагора

АС 2 +ВС 2 =АВ 2 (1)

По условию АС=16, радиус окружности R=10. Если R=10, то АВ=2R=2·10=20.

Тогда из (1) получим:

Пятый вариант задания

Треугольник АВС вписан в окружность с центром в точке О. Найдите угол АСВ, если угол АОВ равен 113 0 . Ответ дайте в градусах.

Решение:

Поскольку вершина О угла АОВ лежит в центре окружности, значит, этот угол центральный. А если так, то он равен величине дуги АВ. Т.е. ᴗАВ=113 0 .

Угол АСВ является вписанным. Следовательно, его величина равна половине дуги, на которую он опирается. Из рисунка видно, что оба угла (АОВ и АСВ) опираются на одну и ту же дугу. Т.к. ᴗАВ=113 0 , то угол АСВ равен

🔥 Видео

Точка O – центр окружности, на которой лежат точки ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

Пятнадцатое задание ОГЭ по математике(12) #огэ #огэ2023 #огэпоматематике #математика #огэматематикаСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

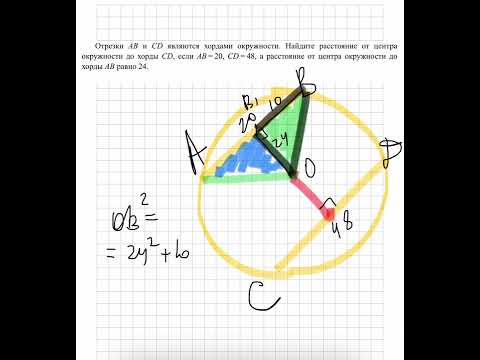
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CDСкачать

ОГЭ 2020 задание 17Скачать

ОГЭ Задание 25 Демонстрационный вариант 2022, математикаСкачать