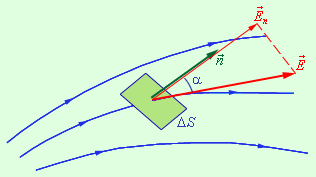
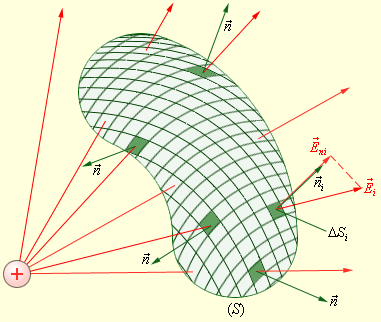
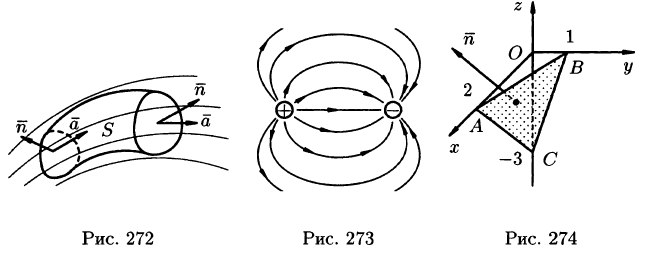
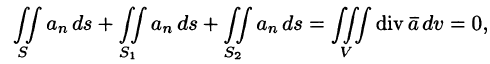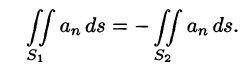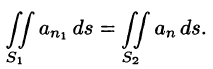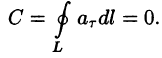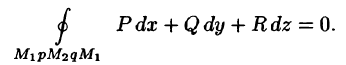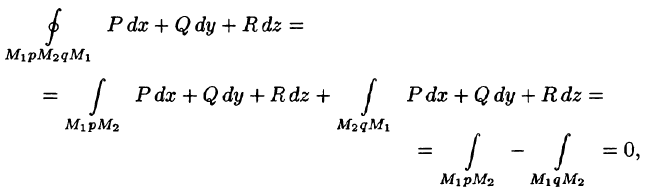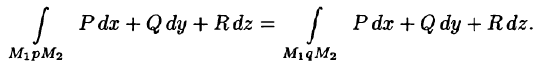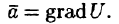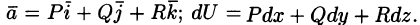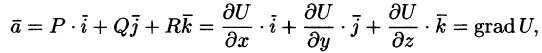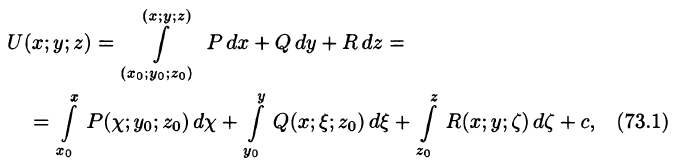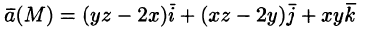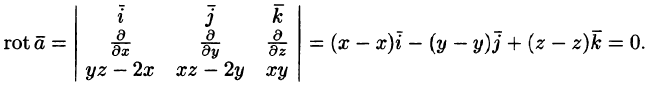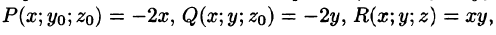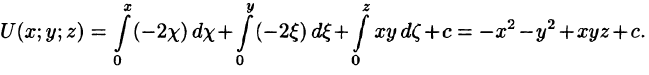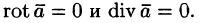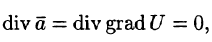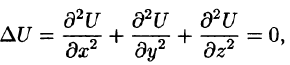Для раскрытия сущности потока векторного поля как характеристики поля, рассмотрим небольшую область физического поля, в котором вектор-функции F поля, например силовые линии, пересекают часть плоскости (гиперповерхности) AS под некоторым углом а к вектору нормали п, перпендикулярному к плоскости (см. рис. 2.2).
Для упрощения будем считать, что в рассматриваемой малой области AS векторное поле однородно, это означает, что его силовые линии (вектор-функции) одинаковы по модулю и направлению, то есть линии параллельны друг другу и их густота везде одинакова.
Рисунок 2.2 — Поток векторного поля, проходящий через плоскость
Проведем через основание вектора нормали плоскость, перпендикулярную вектору F. Эта плоскость обозначена пунктирной линией. Спроектируем поверхность AS на построенную пунктирную плоскость вдоль силовых линий. Очевидно, площадь проекции составит величину, равную AS cos(a). С учетом того, что сила поля выражается густотой силовых линий, т.е. численно равна их количеству через единицу площади, перпендикулярной силовым линиям плоскости, то всего такую площадку, а значит и площадку AS, пересекут N = |f|a5cos(«) силовых линий. Это число силовых линий называется потоком АФ вектора F через поверхность AS:
Для того чтобы получить некий закон с помощью такой меры выбирают общий тип поверхности, а именно — замкнутую поверхность (см. рис. 2.3), которую можно представить в виде участков незамкнутых поверхностей. Принято вектор нормали направлять наружу замкнутой поверхности, тогда «входящие» извне силовые линии образуют отрицательный поток, а «выходящие» изнутри силовые линии образуют положительный поток.
Рисунок 2.3 — Поток силовых линий поля через замкнутую поверхность
Для замкнутой поверхности очевидны две ситуации. Первая ситуация, когда внутри поверхности источники поля, например заряды, отсутствуют. В этом случае силовые линии полей внешних источников, пронизывающие насквозь замкнутую поверхность, создадут «входящий» отрицательный поток и точно такой же по модулю «выходящий» положительный поток, поскольку геометрический смысл потока это просто количество силовых линий, следовательно, суммарный поток будет нулевым.
Вторая ситуация, когда внутри замкнутой поверхности находятся источники Qj, тогда их поля, согласно принципу суперпозиции, просто складываются, и общее количество силовых линий, «выходящих» наружу, прямо пропорционально количеству к источников внутри поверхности. Данная ситуация легко поясняется следующим примером: поток иголок сквозь полиэтиленовый пакет прямо пропорционален количеству ежей в пакете.
Для случая физического поля произвольной конфигурации и замкнутой поверхности S произвольной формы суммарный поток Ф, пронизывающий эту поверхность, равен поверхностному интегралу первого рода по поверхности:
где т — число разбиений поверхности на малые плоские области, в пределах которых поле можно считать однородным.
Полученное выражение (2.2) представляет собой теорему Остро- градского-Гаусса. В классической теорией поля теорема формулируется следующим образом: поток вектора поля сквозь замкнутую поверхность прямо пропорционален количеству источников поля внутри поверхности, т.е. в объеме, ограниченном этой поверхностью. Поле при этом может быть любой природы, например: электрическое, магнитное, гравитационное. Теорема Гаусса — основная теорема электродинамики, которая применяется для вычисления электрических полей, входит в систему уравнений Максвелла.
Физическая интерпретация заключается в том, что поток векторного поля, проходящий сквозь замкнутую поверхность, определяет количество жидкости, протекающей в единицу времени через эту поверхность в положительном направлении (отсюда общий термин «поток»).
Таким образом, установлено, что плоскость, которую пронизывает поток силовых линий, служит одновременно и некоторым «индикатором» наличия поля в данной области пространства. Однако отсутствие потока не всегда означает отсутствие поля, так как силовые линии могут просто лежать в этой плоскости и угол между векторами F и п составит 90 3 , т.е. cos(F,, п,) = 0.
- Теорема Гаусса
- Поток вектора напряженности
- Теорема Гаусса. Доказательство
- Применение теоремы Гаусса
- Теории поля с примерами решения и образцами выполнения
- Скалярное поле
- Производная по направлению
- Векторное поле
- Поток поля
- Дивергенция поля. Формула Остроградского-Гаусса
- Циркуляция поля
- Ротор поля. Формула Стокса
- Оператор Гамильтона
- Векторные дифференциальные операции второго порядка
- Некоторые свойства основных классов векторных полей
- Соленоидальное поле
- Потенциальное поле
- Гармоническое поле
- 💥 Видео
Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Теорема Гаусса
Для полноценного описания электростатического поля заданной системы зарядов в вакууме достаточно экспериментально подтвержденного закона Кулона и принципа суперпозиции. Но при этом существует возможность свойства электростатического поля охарактеризовать в ином обобщенном виде, не опираясь на утверждения касательно кулоновского поля точечного заряда.
Видео:Урок 222. Поток вектора напряженности электрического поляСкачать

Поток вектора напряженности
Зададим новую физическую величину, описывающую электрическое поле – поток Φ вектора напряженности электрического поля. Предположим, что в пространстве, содержащем заданное электрическое поле, имеется некая достаточно малая площадка Δ S .
Элементарный поток вектора напряженности (через площадку S ) – это физическая величина, равная произведению модуля вектора E → , площади Δ S и косинуса угла α между вектором и нормалью к площадке:
Δ Φ = E Δ S cos α = E n Δ S.
В данной формуле E n является модулем нормальной составляющей поля E → .
Рисунок 1 . 3 . 1 . Иллюстрация элементарного потока Δ Φ .
Теперь возьмем для рассмотрения некую произвольную замкнутую поверхность S . Разобьем заданную поверхность на площадки небольшого размера Δ S i , рассчитаем элементарные потоки Δ Φ i поля через эти малые площадки, после чего найдем их сумму, что в итоге даст нам поток Φ вектора через замкнутую поверхность S (рис. 1 . 3 . 2 ):
Φ = ∑ ∆ Φ i = ∑ E m ∆ S i
Когда речь идет о поверхности замкнутого типа, всегда используется внешняя нормаль.
Рисунок 1 . 3 . 2 . Расчет потока Ф через произвольную замкнутую поверхность S .
Видео:Физика. 10 класс. Поток вектора напряженности электрического поля. Теорема Гаусса /18.01.2021/Скачать

Теорема Гаусса. Доказательство
Теорема или закон Гаусса для электростатического поля в вакууме является одним из основных электродинамических законов.
Поток вектора напряженности электростатического поля E → через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε 0 .
Уравнение Гаусса имеет вид:
Φ = 1 ε 0 ∑ q в н у т р
Докажем указанную теорию: для этого исследуем сферическую поверхность (или поверхность шара) S . В центре заданной поверхности расположен точечный заряд q . Любая точка сферы обладает электрическим полем, перпендикулярным поверхности сферы и равным по модулю:
E = E n = 1 4 π ε 0 · q R 2 ,
где R является радиусом сферы.
Поток Φ через поверхность шара запишется, как произведение E и площади сферы 4 π R 2 . Тогда: Φ = 1 ε 0 q .
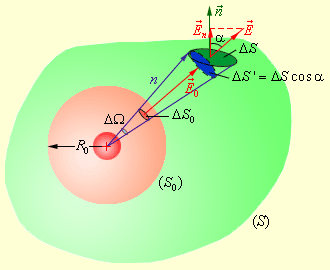
Следующим нашим шагом будет окружение точечного заряда произвольной поверхностью S замкнутого типа; зададим также вспомогательную сферу R 0 (рис. 1 . 3 . 3 ).
Рисунок 1 . 3 . 3 . Поток электрического поля точечного заряда через произвольную поверхность S , окружающую заряд.
Возьмем для рассмотрения конус с малым телесным углом Δ Ω при вершине. Рассматриваемый конус задаст на сфере малую площадку Δ S 0 , а на поверхности S – площадку Δ S . Элементарные потоки Δ Φ 0 и Δ Φ через эти площадки являются одинаковыми. В самом деле:
Δ Φ 0 = E 0 Δ S 0 , Δ Φ = E Δ S cos α = E Δ S ‘ ,
где выражением Δ S ‘ = Δ S cos α определяется площадка, которая задастся конусом с телесным углом Δ Ω на поверхности сферы радиуса n .
Поскольку ∆ S 0 ∆ S ‘ = R 0 2 r 2 , то ∆ Φ 0 = ∆ Φ . Из полученного следует вывод о том, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ 0 через поверхность вспомогательной сферы:
Так же мы можем продемонстрировать, что, когда замкнутая поверхность S не охватывает точечный заряд q , поток Φ равен нулю. Этот случай проиллюстрирован на рис. 1 . 3 . 2 . Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий.
Обобщение теоремы Гаусса на случай произвольного распределения зарядов является следствием из принципа суперпозиции. Поле любого распределения зарядов возможно записать в виде векторной суммы электрических полей точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S сложится из потоков Φ i электрических полей отдельных зарядов. Когда заряд q i расположен внутри поверхности S , он дает вклад в поток, равный q i ε 0 . В случае расположения заряда снаружи поверхности его вклад в поток есть нуль.
Так, мы доказали теорему Гаусса.
Теорема Гаусса, по сути, есть следствие закона Кулона и принципа суперпозиции. Однако, взяв за изначальную аксиому утверждения теоремы, следствием станет закон Кулона, в связи с чем теорему Гаусса порой называют альтернативной формулировкой закона Кулона.
Опираясь на теорему Гаусса, в определенных случаях легко определить напряженность электрического поля вокруг заряженного тела (при наличии заранее угаданных симметрии заданного распределения зарядов и общей структуры поля).
Видео:Вектор Умова-Пойнтинга ● 1Скачать

Применение теоремы Гаусса
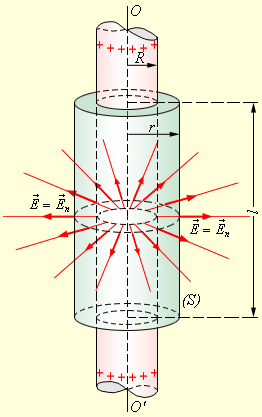
В качестве примера можно рассмотреть задачу, в которой необходимо вычислить поле тонкостенного полого однородно заряженного длинного цилиндра с радиусом R . Такая задача имеет осевую симметрию, и из соображений симметрии электрическое поле должно иметь направление по радиусу. Таким образом, чтобы иметь возможность применить теорему Гаусса, оптимально выбрать поверхность замкнутого типа S в виде соосного цилиндра некоторого радиуса r и длины l , закрытого с обоих торцов (рис. 1 . 3 . 4 ).
Рисунок 1 . 3 . 4 . Иллюстрация поля однородно заряженного цилиндра. O O ‘ – ось симметрии.
Если r ≥ R , то весь поток вектора напряженности пройдет через боковую поверхность цилиндра, поскольку поток через оба основания есть нуль. Формула площади боковой поверхности цилиндра запишется как: 2 π r l . Применим закон Гаусса и получим:
Φ = E 2 π r l = τ l ε 0 .
В указанном выражении τ является зарядом длины цилиндра. Далее можно записать:
Данное выражение не имеет зависимости от радиуса R заряженного цилиндра, а значит оно применимо и к полю длинной однородно заряженной нити.
Чтобы найти напряженность поля внутри заряженного цилиндра, необходимо создать замкнутую поверхность для случая r R . В соответствии с симметрией задачи поток вектора напряженности через боковую поверхность цилиндра должен быть, и в этом случае он равен Φ = E 2 π r l . Исходя из гауссовской теоремы, этот поток находится в пропорции к заряду, расположенному внутри замкнутой поверхности. Заряд этот равен нулю, откуда вытекает, что электрическое поле внутри однородно заряженного длинного полого цилиндра тоже есть нуль.
Точно так же теорема и формула Гаусса применимы для определения электрического поля в иных случаях, когда распределение зарядов охарактеризовано какой-либо симметрией, к примеру, симметрией относительно центра, плоскости или оси. Во всех этих случаях необходимо выбирать замкнутую гауссову поверхность подходящей формы.
К примеру, в случае центральной симметрии поверхность оптимально выбрать в виде сферы, у которой центр расположен в точке симметрии. Когда мы имеем симметрию относительно оси, подходящим видом замкнутой поверхности будет соосный цилиндр, закрытый с обоих торцов (аналогично рассмотренному выше примеру).
При отсутствии симметрии и невозможности угадать общую структуру поля, теорема Гаусса не сможет быть применена для упрощения решения задачи по определению напряженности поля.
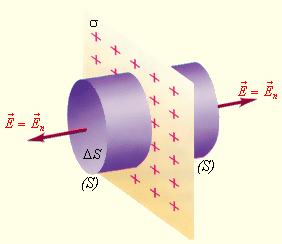
Разберем еще пример распределения зарядов при наличии симметрии: нахождение поля равномерно заряженной плоскости (рис. 1 . 3 . 5 ).
Рисунок 1 . 3 . 5 . Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность.
Здесь гауссову поверхность S оптимально задать как цилиндр некой длины, замкнутый с обоих концов. Ось цилиндра является перпендикуляром к заряженной плоскости; в свою очередь, торцы цилиндра находятся на одинаковом расстоянии от нее. В соответствии с симметрией поле равномерно заряженной плоскости должно везде иметь направление по нормали. Применим теорему Гаусса и получим:
2 E ∆ S = σ ∆ S ε 0 или E = σ 2 ε 0 .
Здесь σ является поверхностной плотностью заряда или зарядом, приходящимся на единицу площади.
Выражение, которое мы получили для электрического поля однородно заряженной плоскости, возможно использовать и для плоских заряженных площадок конечного размера: здесь расстояние от точки, в которой мы определяем напряженность поля, до заряженной площадки должно быть значимо меньше размеров площадки.
Видео:Билет №38 "Поток энергии"Скачать

Теории поля с примерами решения и образцами выполнения
Теория поля — крупный раздел физики, механики, математики, в котором изучаются скалярные, векторные, тензорные поля.
К рассмотрению скалярных и векторных полей приводят многие задачи физики, электротехники, математики, механики и других технических дисциплин. Изучение одних физических полей способствует изучению и других. Так, например, силы всемирного тяготения, магнитные, электрические силы — все они изменяются обратно пропорционально квадрату расстояния от своего источника; диффузия в растворах происходит по законам, общим с распространением тепла в различных средах; вид силовых магнитных линий напоминает картину обтекания препятствий жидкостью и т. д.
Математическим ядром теории поля являются такие понятия, как градиент, поток, потенциал, дивергенция, ротор, циркуляция и другие. Эти понятия важны и в усвоении основных идей математического анализа функций многих переменных.
Полем называется область V пространства, в каждой точке которой определено значение некоторой величины. Если каждой точке М этой области соответствует определенное число U = U(M), говорят, что в области определено (задано) скалярное поле (или функция точки). Иначе говоря, скалярное поле — это скалярная функция U(М) вместе с ее областью определения. Если же каждой точке М области пространства соответствует некоторый вектор 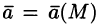
Примерами скалярных полей могут быть поля температуры (воздуха, тела, …), атмосферного давления, плотности (массы, воздуха, …), электрического потенциала и т.д. Примерами векторных полей являются поле силы тяжести, поле скоростей частиц текущей жидкости (ветра), магнитное поле, поле плотности электрического тока и т. д.
Если функция 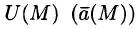
Далее будем рассматривать только стационарные поля.
Если V — область трехмерного пространства, то скалярное поле U можно рассматривать как функцию трех переменных х, у, z (координат точки М):
(Наряду с обозначениями 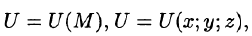
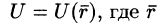
Если скалярная функция U (М) зависит только от двух переменных, например х и у, то соответствующее скалярное поле U(х; у) называют плоским.
Аналогично: вектор 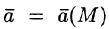
Вектор 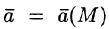
где P(x;y;z), Q(x;y;z ), R(x;y;z) — проекции вектора 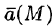
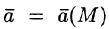
Векторное поле называется однородным, если 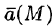
В дальнейшем будем предполагать, что скалярные функции (U(x;y;z) — определяющая скалярное поле, P(x;y;z), Q(x;y;z) и R(x; у; z) — задающие векторное поле) непрерывны вместе со своими частными производными.
Пример:
Функция 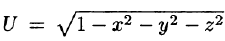
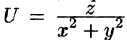
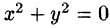
Пример:
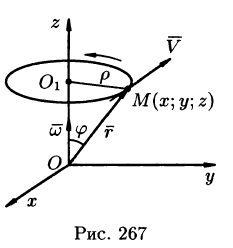
Найти поле линейной скорости 
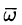
Решение:
Угловую скорость представим в виде вектора 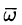
Построим радиус-вектор 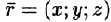
Численное значение линейной скорости 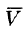
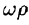
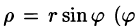
Вектор скорости 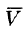
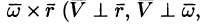
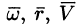
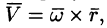
или
Поле линейных скоростей 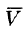
Видео:ДивергенцияСкачать

Скалярное поле
Поверхности и линии уровня:
Рассмотрим скалярное поле, задаваемое функцией U = U(x,y,z). Для наглядного представления скалярного поля используют поверхности и линии уровня.
Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция U(М) принимает постоянное значение, т. е.
Давая в уравнении (70.1) величине с различные значения, получим различные поверхности уровня, которые в совокупности как бы расслаивают поле. Через каждую точку поля проходит только одна поверхность уровня. Ее уравнение можно найти путем подстановки координат точки в уравнение (70.1).
Для скалярного поля, образованного функцией
поверхностями уровня является множество концентрических сфер с центрами в начале координат: 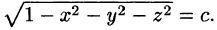
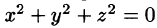
Для равномерно раскаленной нити поверхности уровня температурного поля (изотермические поверхности) представляют собой круговые цилиндры, общей осью которых служит нить.
В случае плоского поля U — U(х; у) равенство U(x; у) = с представляет собой уравнение линии уровня поля, т. е. линия уровня —это линия на плоскости Оху, в точках которой функция U (х; у) сохраняет постоянное значение.
В метеорологии, например, сети изобар и изотерм (линии одинаковых средних давлений и одинаковых средних температур) являются линиями уровня и представляют собой функции координат точек местности.
Линии уровня применяются в математике при исследовании поверхностей методом сечений (см. п. 12.9).
Производная по направлению
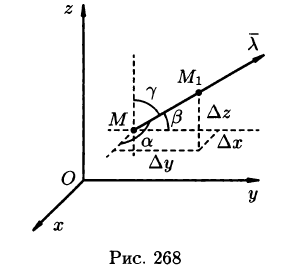
Для характеристики скорости изменения поля U =U(М) в заданном направлении введем понятие «производной по направлению».
Возьмем в пространстве, где задано поле U = U(x;y;z), некоторую точку М и найдем скорость изменения функции U при движении точки М в произвольном направлении 
Приращение функции U, возникающее при переходе от точки М к некоторой точке 
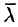
Производной от функции U = U(M) в точке М по направлению 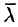
Производная по направлению 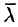
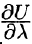
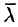
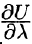
где 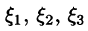
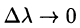
Переходя к пределу при 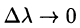
В случае плоского поля U = U(x;y) имеем:
Формула (70.2) принимает вид:
Замечание:
Понятие производной по направлению является обобщением понятия частных производных 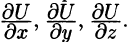
Пример:
Найти производную функции 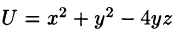
Решение:
Находим вектор 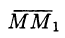
Находим частные производные функции и вычисляем их значения в точке М:
Следовательно, по формуле (70.2) имеем:
Поскольку jj^- Градиент скалярного поля и его свойства
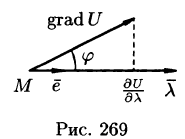
В каком направлении 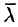
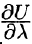
Можно заметить, что правая часть равенства (70.2) представляет собой скалярное произведение единичного вектора
и некоторого вектора
Вектор, координатами которого являются значения частных производных функции U(x,y,z) в точке M(x;y,z), называют градиентом функции и обозначают gradU, т. е.
Отметим, что grad U есть векторная величина. Говорят: скалярное поле U порождает векторное поле градиента U. Теперь равенство (70.2) можно записать в виде
где 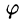
Из формулы (70.3) сразу следует, что производная по направлению достигает наибольшего значения, когда 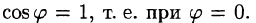
В этом состоит физический смысл градиента. На указанном свойстве градиента основано его широкое применение в математике и других дисциплинах.
Приведем важные свойства градиента функции.
1.Градиент направлен по нормали к поверхности уровня, проходящей через данную точку.
Действительно, по любому направлению вдоль поверхности уровня 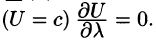
Доказываются эти свойства на основании определения градиента. Докажем, например, последнее свойство. Имеем:
Замечание. Приведенные свойства градиента функции остаются справедливыми и для плоского поля.
Пример:
Найти наибольшую скорость возрастания функции
Решение:
Наибольшая скорость возрастания функции равна
Отметим, что функция U будет убывать с наибольшей скоростью 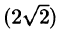
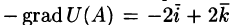
Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. Практическая часть. 10 класс.Скачать

Векторное поле
Векторные линии поля:
Рассмотрим векторное поле, задаваемое вектором 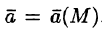
Векторной линией поля 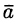
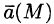
Это понятие для конкретных полей имеет ясный физический смысл. Например, в поле скоростей текущей жидкости векторными линиями будут линии, по которым движутся частицы жидкости (линии тока); для магнитного поля векторными (силовыми) линиями будут линии, выходящие из северного полюса и оканчивающиеся в южном.
Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называется векторной трубкой.
Изучение векторного поля обычно начинают с изучения расположения его векторных линий. Векторные линии поля
описываются системой дифференциальных уравнений вида
Действительно, пусть PQ — векторная линия поля, 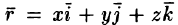
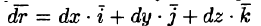
Пример:
Найти векторные линии поля линейных скоростей тела, вращающегося с постоянной угловой скоростью 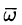
Решение:
Это поле определено вектором 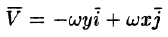
Интегрируя, получим: 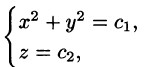
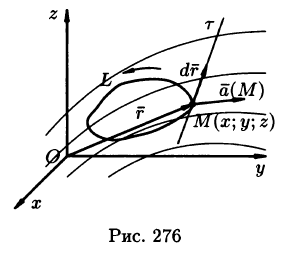
Поток поля
Пусть векторное поле образовано вектором (71.1). Для наглядности будем считать 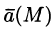
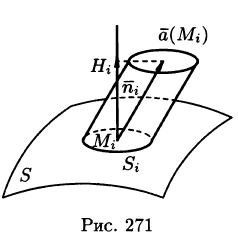
Выберем определенную сторону поверхности S. Пусть 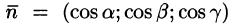
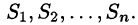
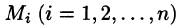
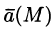
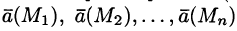
Будем приближенно считать каждую площадку плоской, а вектор 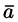
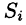
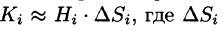
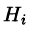
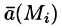
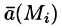
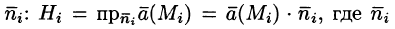
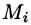
Точное значение искомого количества жидкости получим, взяв предел найденной суммы при неограниченном увеличении числа элементарных площадок и стремлении к нулю их размеров (диаметров 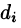
Независимо от физического смысла поля 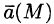
Потоком вектора 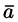
Рассмотрим различные формы записи потока вектора. Так как
где 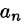
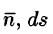
Иногда формулу (71.3) записывают в виде
где вектор 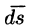
— проекции вектора 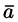
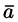
Используя взаимосвязь поверхностных интегралов I и II рода (см. формулу (58.8)), поток вектора можно записать как
Отметим, что поток К вектора а есть скалярная величина. Величина К равна объему жидкости, которая протекает через поверхность S за единицу времени. В этом состоит физический смысл потока (независимо от физического смысла поля).
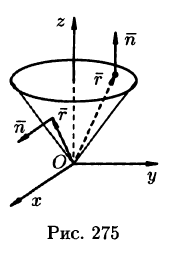
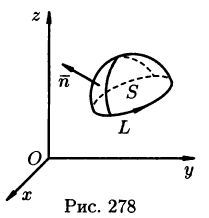
Особый интерес представляет случай, когда поверхность замкнута и ограничивает некоторый объем V. Тогда поток вектора записывается в виде
В этом случае за направление вектора п обычно берут направление внешней нормали и говорят о потоке изнутри поверхности S (см. рис. 272).
Если векторное поле 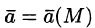
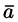
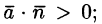
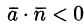
При этом если К > 0, то из области V вытекает больше жидкости, чем в нее втекает. Это означает, что внутри области имеются дополнительные источники.
Если К
Пример:
Найти поток вектора 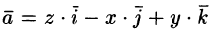
Решение:
Поток найдем методом проектирования на три координатные плоскости. Для этого воспользуемся формулой (71.5). В нашем случае Р = z, Q = —х, R = у. Имеем:
Расчленим этот поверхностный интеграл на три слагаемых, затем сведем их вычисление к вычислению двойных интегралов. Нормаль к верхней стороне треугольника образует с осью Ох тупой угол, с осью Оу — тупой, а с осью Oz — острый угол. (Единичный вектор данной плоскости есть 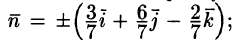
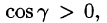
Итак, 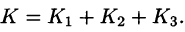
В результате имеем:
Пример:
Найти поток радиус-вектора 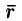
Решение:
Очевидно, что
т. к.
Дивергенция поля. Формула Остроградского-Гаусса
Важной характеристикой векторного поля (71.1) является так называемая дивергенция, характеризующая распределение и интенсивность источников и стоков поля.
Дивергенцией (или расходимостью) векторного поля
в точке М называется скаляр вида 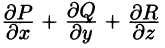
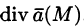
Отметим некоторые свойства дивергенции.
- Если
— постоянный вектор, то
где с = const.
т. е. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
- Если U — скалярная функция,
— вектор, то
Эти свойства легко проверить, используя формулу (71.6). Докажем, например, справедливость свойства 4.
Так как 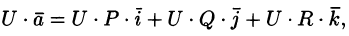
Используя понятия потока и дивергенции векторного поля, запишем известную в анализе (см. (58.9)) формулу Остроградского-Гаусса
в так называемой векторной форме.
Рассматривал область V, ограниченную замкнутой поверхностью S, в векторном поле (71.1), можно утверждать, что левая часть формулы (71.7) есть поток вектора 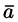
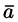
(в котором она чаще всего и встречается).
Формула Остроградского-Гаусса означает, что поток векторного поля через замкнутую поверхность S (в направлении внешней нормали, т. е. изнутри) равен тройному интегралу от дивергенции этого поля по объему V, ограниченному данной поверхностью.
Используя формулу (71.8), можно дать другое определение дивергенции векторного поля 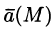
По теореме о среднем для тройного интеграла (см. п. 54.1) имеем:
где 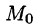
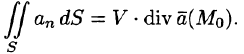
Пусть поверхность S стягивается в точку. Тогда 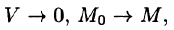
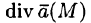
Дивергенцией векторного поля в точке М называется предел отношения потока поля через (замкнутую) поверхность S, окружающую точку М, к объему тела, ограниченного этой поверхностью, при условии, что вся поверхность стягивается в точку
Определение (71.9) дивергенции эквивалентно (можно показать) определению (71.6).
Как видно из определения, дивергенция векторного поля в точке является скалярной величиной. Она образует скалярное поле в данном векторном поле.
Исходя из физического смысла потока (обычно условно считают, что 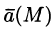
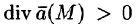
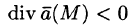
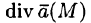
Понятно, что если в объеме V, ограниченном замкнутой поверхностью S, нет ни источников, ни стоков, то
Векторное поле, в каждой точке которого дивергенция поля равна нулю, т. е. 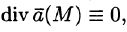
Пример:
Найти дивергенцию поля линейных скоростей 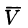
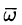
Решение:
Примем ось вращения жидкости за ось Oz. Тогда, как показано ранее (см. пример 69.2), 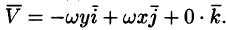
Поле 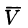
Циркуляция поля
Пусть векторное поле образовано вектором (71.1). Возьмем в этом поле некоторую замкнутую кривую L и выберем на ней определенное направление.
Пусть 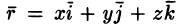
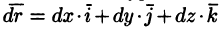
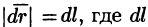
Криволинейный интеграл по замкнутому контуру L от скалярного произведения вектора 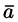
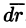

Рассмотрим различные формы записи циркуляции. Так как
где 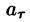
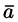
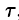
Циркуляция С, записанная в виде (71.12) имеет простой физический смысл: если кривая L расположена в силовом поле, то циркуляция — это работа силы 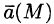
Отметим, что вдоль замкнутых векторных линий циркуляция отлична от нуля, потому что в каждой точке векторной линии скалярное произведение 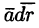
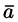
Пример:
Найти циркуляцию вектора поля линейных скоростей вращающегося тела (см. пример 69.2) 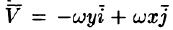
Решение:
Будем считать, что направление нормали к плоскости 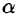
где S — площадь поверхности, ограниченной кривой L (см. 56.17).
Заметим, что если нормаль к поверхности S образует угол 
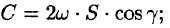
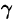
Пример:
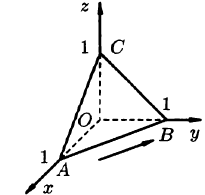
Вычислить циркуляцию векторного поля
вдоль периметра треугольника с вершинами A(1;0;0), В(0;1;0), С(0;0;1) (см. рис. 277).
Решение:
Согласно формуле (71.12), имеем:
На отрезке AB: x + у = 1, z = 0, следовательно,
На отрезке ВС: у + z = 1, х = 0, следовательно,
На отрезке СА: х + z = 1, у = 0, следовательно,
Ротор поля. Формула Стокса
Ротором (или вихрем) векторного поля
называется вектор, обозначаемый 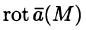
Формулу (71.13) можно записать с помощью символического определителя в виде, удобном для запоминания:
Отметим некоторые свойства ротора.
- Если
— постоянный вектор, то
т. е. ротор суммы двух векторов равен сумме роторов слагаемых.
- Если U — скалярная функция, а
— векторная, то
Эти свойства легко проверить, используя формулу (71.13). Покажем, например, справедливость свойства 3:
Используя понятия ротора и циркуляции, векторного поля, запишем известную в математическом анализе (см. п. 58.4) формулу Стокса:
Левая часть формулы (71.14) представляет собой циркуляцию вектора 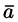
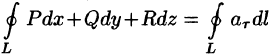
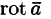
Следовательно, формулу Стокса можно записать в виде
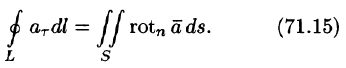
Такое представление формулы Стокса называют ее векторной формой. В этой формуле положительное направление на контуре L и выбор стороны у поверхности S согласованы между собой так же, как в теореме Стокса.
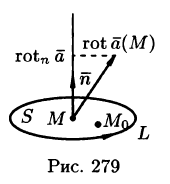
Формула (71.15) показывает, что циркуляция вектора 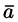
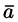
Используя формулу (71.14), можно дать другое определение ротора поля, эквивалентное первому и не зависящее от выбора координатной системы.
Для этого применим формулу Стокса (71.15) для достаточно малой плоской площадки S с контуром L, содержащей точку М.
По теореме о среднем для поверхностного интеграла (п. 57.1, свойство 7) имеем:
где 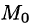
Тогда формулу (71.15) можно записать в виде
Пусть контур L стягивается в точку М. Тогда 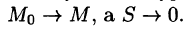
Ротором вектора 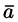
Как видно из определения, ротор вектора 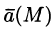
Дадим физическое истолкование понятия ротора векторного поля. Найдем ротор поля линейных скоростей твердого тела, вращающегося вокруг оси Oz с постоянной угловой скоростью (пример 69.2) 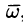
По определению ротора
Ротор этого поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости вращения.
С точностью до числового множителя ротор поля скоростей 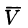
Замечание:
Из определения (71.13) ротора вытекает, что направление ротора — это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке S.
Так что связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению (см. п. 70.3).
Оператор Гамильтона
Векторные дифференциальные операции первого порядка:
Основными дифференциальными операциями (действиями) над скалярным полем U и векторным полем 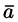
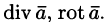
Эти операции удобно записывать с помощью так называемого оператора Гамильтона
Этот символический вектор называют также оператором 

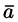
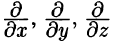
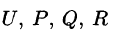
Применяя оператор Гамильтона, получим дифференциальные операции первого порядка:
Оператор Гамильтона применяется для записи и других операций и для вывода различных формул в теории поля. При действиях с ним надо пользоваться правилами векторной алгебры и правилами дифференцирования.
В частности, производная по направлению (70.2) может быть записана в виде
где
Векторные дифференциальные операции второго порядка
После применения оператора Гамильтона к скалярному или векторному полю получается новое поле, к которому можно снова применить этот оператор. В результате получаются дифференциальные операции второго порядка. Нетрудно убедиться, что имеется лишь пять дифференциальных операций второго порядка:
(Понятно, что операция 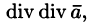
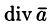
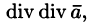
Запишем явные выражения для дифференциальных операций второго порядка, используя оператор Гамильтона. Заметим при этом, что оператор действует только на множитель, расположенный непосредственно за оператором.
Правая часть этого равенства называется оператором Лапласа скалярной функции U и обозначается 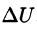
Дифференциальное уравнение Лапласа 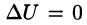
Замечание. К равенству (72.1) можно прийти, введя в рассмотрение скалярный оператор дельта:
(который тоже называют оператором Лапласа).
2. 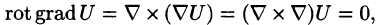
4. 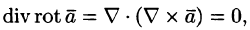
так как двойное векторное произведение обладает свойством
Здесь 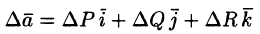
Некоторые свойства основных классов векторных полей
Соленоидальное поле
Напомним, что векторное поле 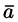
Примерами соленоидальных полей являются: поле линейных скоростей вращающегося твердого тела (см. пример 71.4); магнитное поле, создаваемое прямолинейным проводником, вдоль которого течет электрический ток, и другие.
Приведем некоторые свойства соленоидального поля.
- В соленоидальном поле
поток вектора через любую замкнутую поверхность равен нулю. Это свойство непосредственно вытекает из формулы (71.8). Таким образом, соленоидальное поле не имеет источников и стоков.
- Соленоидальное поле является полем ротора некоторого векторного поля, т. е. если
, то существует такое поле
, что
. Вектор
называется векторным потенциалом поля
.
Любое из свойств 1-2 можно было бы взять в качестве определения соленоидального поля.
Доказывать свойство 2 не будем. Отметим лишь, что обратное утверждение — поле ротора векторного поля есть соленоидальное — нами доказано (выше мы показали, что 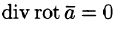
3. В соленоидальном поле 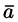
Рассмотрим векторную трубку между двумя ее произвольными сечениями 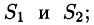
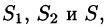
где n — внешняя нормаль.
Так как на боковой поверхности векторной трубки нормаль п перпендикулярна к векторам поля, то 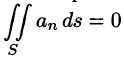
Переменив направление нормали на площадке 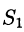
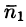
В поле скоростей текущей жидкости полученный результат означает, что количество жидкости, втекающей в трубку за единицу времени, равно количеству жидкости, вытекающей из нее.
Потенциальное поле
Векторное поле 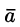
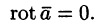
Приведем основные свойства потенциального поля.
Свойство 1. Циркуляция потенциального поля 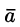
Это непосредственно вытекает из формулы (71.14). Следовательно,
В частности, для силового потенциального поля это означает, что работа силы по любому замкнутому контуру равна нулю; в поле скоростей текущей жидкости равенство С = 0 означает, что в потоке нет замкнутых струек, т. е. нет водоворотов.
Свойство 2. В потенциальном поле 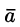
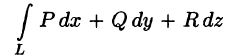
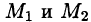
Это свойство вытекает из свойства 1. Действительно, взяв в поле две точки 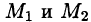
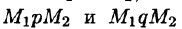
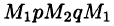
Учитывая свойства криволинейного интеграла, получаем:
Свойство 3. Потенциальное поле является полем градиента некоторой скалярной функции U(x; y; z), т. е. если 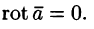
Из равенства 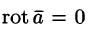
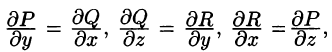
Отсюда: 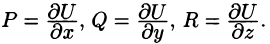
т. е. вектор поля 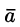
Замечание. Из равенства rot grad U = 0 следует обратное утверждение — поле градиента скалярной функции U = U(x;y; z) является потенциальным.
Из равенства 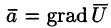
где 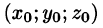
Произвольное же векторное поле требует задания трех скалярных функций (P(x;y;z), Q(x;y;z), R(x;y,z) — проекции вектора поля на оси координат).
Замечание. Определение потенциального поля может быть дано иначе — векторное поле 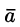
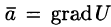
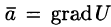
Пример:
Установить потенциальность поля
и найти его потенциал.
Решение:
Следовательно, поле вектора 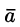
Найдем потенциал U по формуле (73.1), выбирая в качестве фиксированной точки начало координат, т. е. 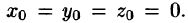
Гармоническое поле
Векторное поле 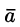
Примером гармонического поля является поле линейных скоростей стационарного безвихревого потока жидкости при отсутствии в нем источников и стоков.
Так как поле 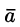
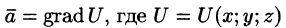
Но так как поле одновременно и соленоидальное, то
или, что то же самое,
т. е. потенциальная функция U гармонического поля а является решением дифференциального уравнения Лапласа. Такая функция называется, как уже упоминали, гармонической.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
💥 Видео
Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

Туннель сквозь Землю? | Теорема Остроградского-Гаусса и её физический смыслСкачать

Билет №02 "Теорема Гаусса"Скачать

Александр Чирцов: ротор, дивергенция и градиентСкачать

Урок 223. Теорема ГауссаСкачать

Еще раз про поток и циркуляциюСкачать

Дивергенция векторного поляСкачать

ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Урок 225. Задачи на поток вектора напряженности электрического поляСкачать

Электромагнитная индукция. Простыми словамиСкачать

Дивергенция векторного поля. Гидродинамическая аналогия. Теорема Остроградского.Скачать






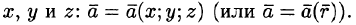
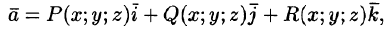
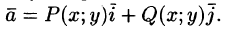
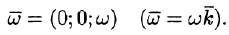
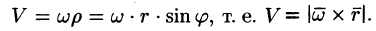
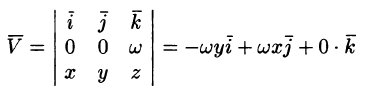
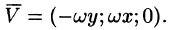


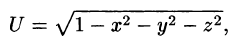
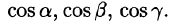
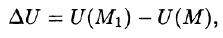
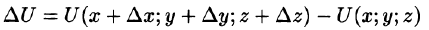
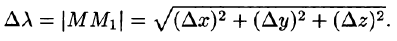
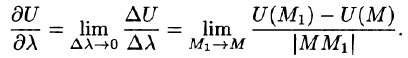
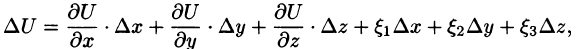
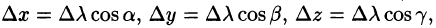
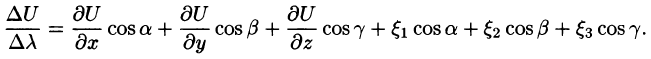
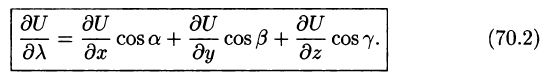
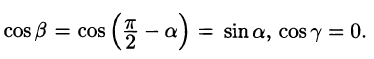
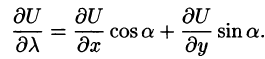
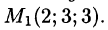
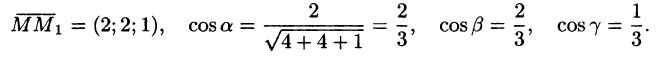
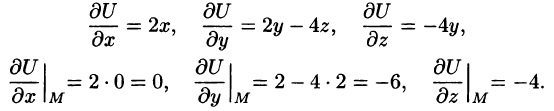
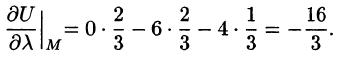
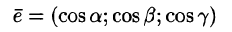
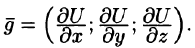
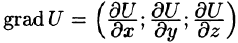
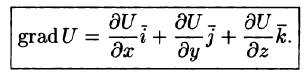
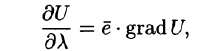
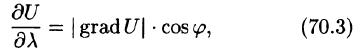
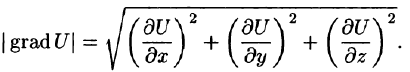
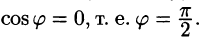
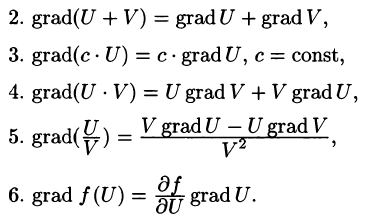
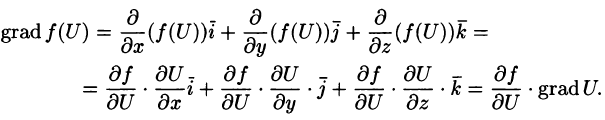
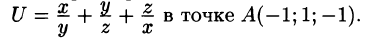
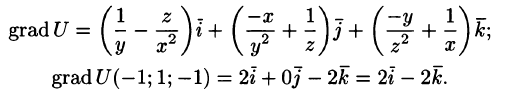
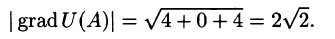
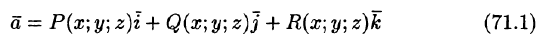
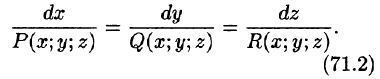
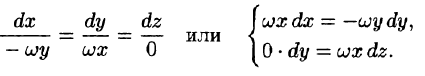
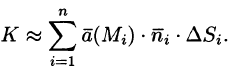
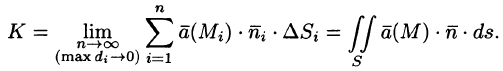

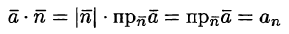

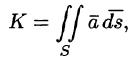
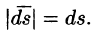
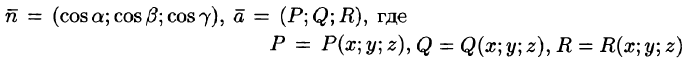
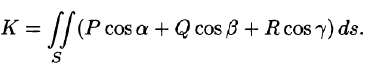
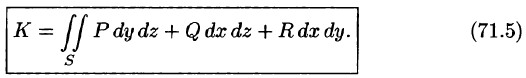
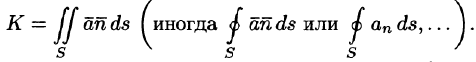
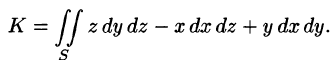
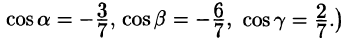
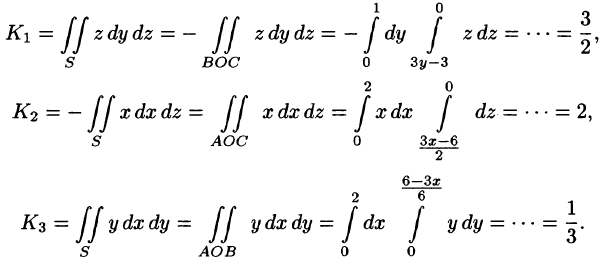
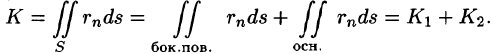
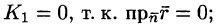
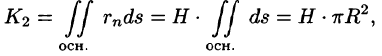
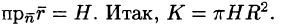
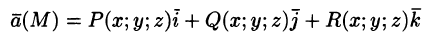
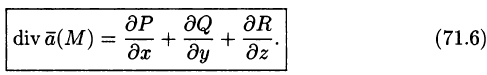
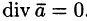
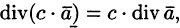 где с = const.
где с = const.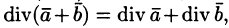 т. е. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
т. е. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.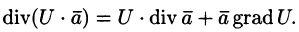
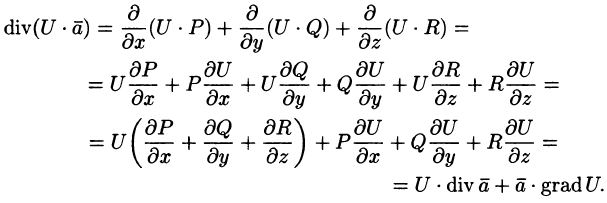
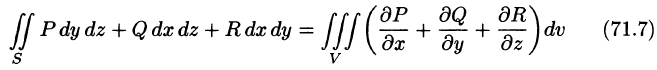
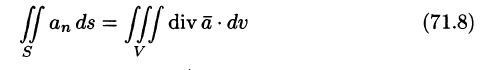
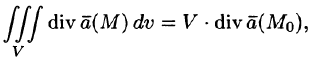
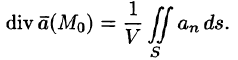
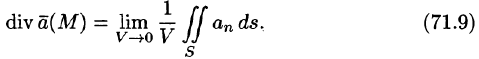
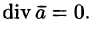
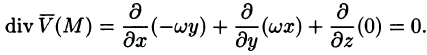
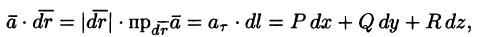

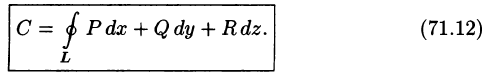
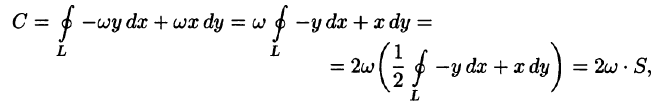
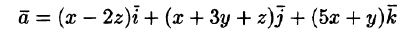
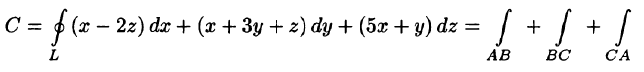
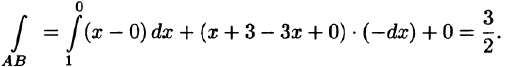
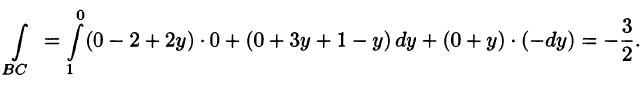
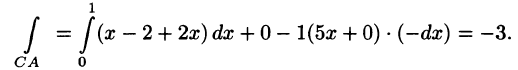
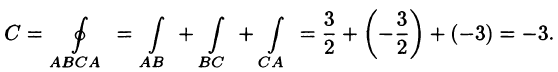
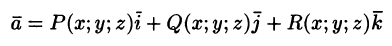
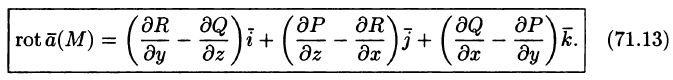
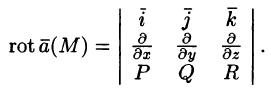
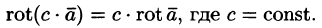
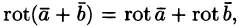 т. е. ротор суммы двух векторов равен сумме роторов слагаемых.
т. е. ротор суммы двух векторов равен сумме роторов слагаемых.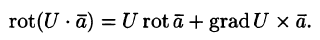
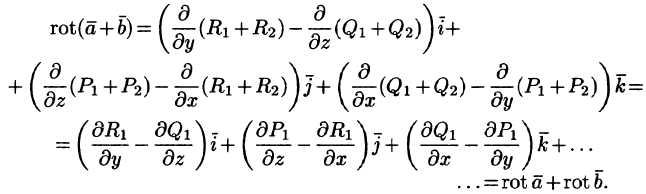
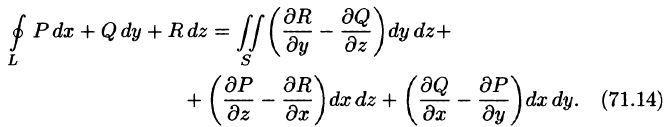
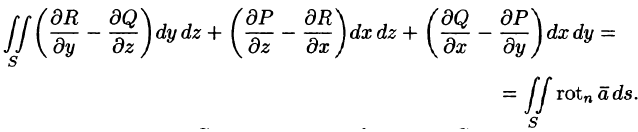
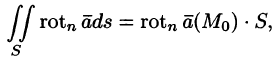
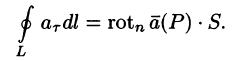
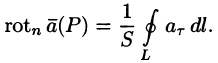
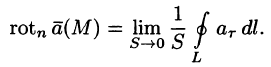
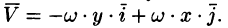
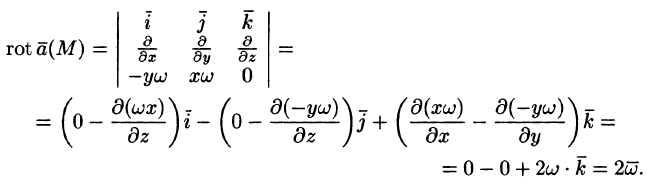
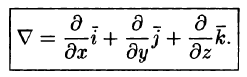
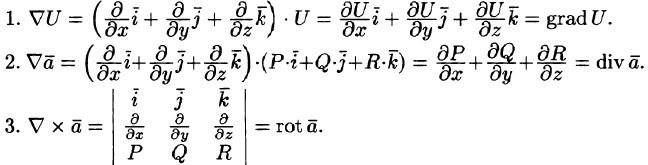
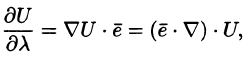
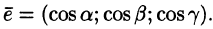
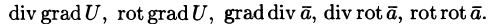
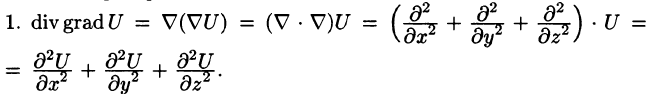
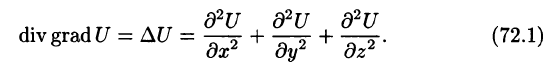
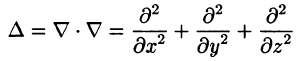
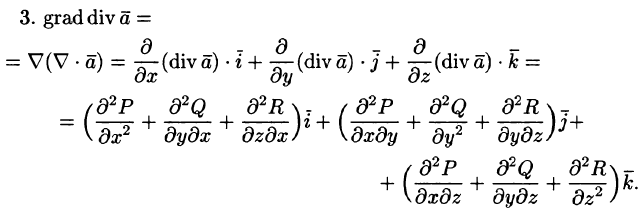
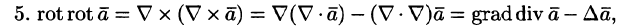
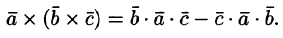
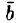 , что
, что 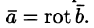 . Вектор
. Вектор