Полная система векторов что это

Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

Линейная зависимость векторов

Пусть задано множество векторов в линейном пространстве L

(1)

и некоторый ненулевой (если хотя бы одна из ) набор чисел

. (2)

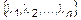
Вектор называется линейной комбинацией векторов системы (1), если он равен сумме попарных произведений векторов системы (1) с соответствующим числом набора (2).

(3)

.

Система векторов (1) называется линейно-зависимой, если существует ненулевой набор чисел (2), такой, что линейная комбинация векторов (1) равна нуль-вектору.

. (4)

Если же равенство (4) выполняется только при всех , то система векторов (1) называется линейно-независимой.

Для векторов , , запишем: , , следовательно векторы — линейно-зависимы.

Если среди векторов системы (1) есть хотя бы один , система линейно-зависима. Пусть , для и . Пусть по условию. Тогда , следовательно, система (1) линейно-зависима.

Теорема 1 (критерий линейной зависимости векторов).

Для того чтобы система векторов была линейно-зависима, необходимо и достаточно, чтобы какой-нибудь вектор системы можно было представить в виде линейной комбинации других векторов системы.

Необходимость. Дана линейно-зависимая система (1). Требуется доказать, что . Из определения 2 следует, что

(5)

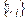
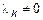
при ненулевом наборе . Пусть . Из (5) можно найти :

.

. (6)

Требуется доказать, что система (1) линейно-зависима. Из (6) следует, что , , а так как , то набор (2) ненулевой, а система (1) линейно-зависима.

Два вектора линейно зависимы тогда и только тогда, когда они коллинеарные, т. е. – линейно-зависимы , т. к. по условию коллинеарности следует, что , откуда по теореме – линейно-зависимы.

2. Условия линейной зависимости векторов

Три вектора линейно-зависимы тогда и только тогда, когда они компланарны, т. е. – линейно-зависимы .

Доказательство.

Необходимость. Дано – линейно-зависимы. Доказать: . Из теоремы 1 следует, что , где – числа. По определению , , следовательно, пл. ( ), .

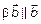
Достаточность. Дано: . Доказать, что – линейно-зависимы. Представим три вектора в одной плоскости (рис.1). На основаниях векторов построим параллелограмм так, чтобы вектор был диагональю этого параллелограмма ONKM. Тогда , следовательно, по теореме 1 – линейно-зависимы.

Любые четыре вектора в линейно-зависимы.

Изобразим произвольно 4 вектора в пространстве. По рис. 2 . Следовательно, по теореме 1, – линейно-зависимы.

3. Базис пространств

Дана система векторов в L . (7)

Система B называется полной, если ее объединение с любым вектором этого пространства образует линейно-зависимую систему. – полная, если – линейно-зависимы, , .

Полная, линейно независимая система векторов в пространстве называется базисом этого пространства.

Если и не коллинеарные, то в они образуют базис. По определению они линейно-независимые. Это полная система потому, что присоединение 3-го вектора приведет к образованию трех компланарных векторов в , а следовательно, согласно теореме 2 они линейно-зависимы.

Из теоремы 1 и определения 4 следует, что любой вектор 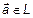можно представить в виде линейной комбинации базисных векторов:

. (8)

Выражение (8) называется разложением вектора в данном базисе, а числа – координатами в базисе B: . В чаще всего принимают базис, векторы которого ортогональны.

, . (9)

Теорема 4 (единственности разложения вектора в базисе).

Разложение вектора в данном базисе единственно.

Доказательство (от противного).

Предположим, что верно (8) и верно

, (10)

где хотя бы для одного i. Вычтем из (8) равенство (10) — = . Следовательно, система B линейно-зависима, а это противоречит тому, что система B – базис. Предположение не верно, т. е. для любых i, значит, разложение единственное.

Число векторов базиса называется размерностью пространства.

Из теоремы 2 следует, что 3 некомпланарных вектора образуют базис (трехмерное пространство).

4. Элементы теории проекций

Проекцией вектора на ось l ,если он сонаправлен с вектором , называется число, равное длине вектора , и противоположное число, если направление противоположно ( , если , и — , если ).

= ,

где .

Теорема 5. .

Теорема 6. .

5. Декартов базис

В за базис примем , где ; , – декартов базис. Тогда любой вектор можно разложить в этом базисе (рис. 4).

, (11)

где – координаты в базисе.

Координаты вектора равны проекциям на соответствующие оси.

Из

. (12)

Согласно теореме 4 данное разложение (12) единственное. Из по определению нормы в следует, что , , где , , .

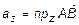
Радиус-вектором точки называется вектор, соединяющий начало координат с этой точкой. Обозначается для точки как ; .

Пусть даны точки и . Их соответствующие радиус-векторы равны и (рис. 4). Из получим . Для проекции на Ox имеем

.

Аналогичные рассуждения можно провести для остальных проекций. Тогда получим:

(13)

Координаты вектора равны разности координат конца и начала вектор:

. (14)

6. Полярная система координат

В полярной системе координат вектор задается следующим образом. Задается его длина и угол поворота, отложенный от положительного направления оси . Положительный угол считается при повороте против часовой стрелки. Задать вектор в полярных координатах означает задать его норму и угол (рис. 5). То есть – формула Эйлера, где i= – мнимая единица. Данные вопросы относятся к теории комплексных чисел и будут изучаться позже. В соответствии с рис. 5 можно привести формулы, связывающие декартову и полярные системы координат: , . Окончательно получим

. (15)

В лекции векторная алгебра освящена на более высоком уровне. Декартова система координат представлена на основе теории проекций. Это дает более глубокое понимание вектора в трехмерном пространстве. Введено фундаментальное понятие «базис». Отметим следующее:

— размерность пространства определяется его базисом;

— линейная зависимость означает возможность представить один вектор в виде линейной комбинации других векторов;

— базис может быть и не ортогональным;

— разложение в данном базисе единственное;

— существуют другие системы координат.

1. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001.

2. Рыжков В. В. Лекции по аналитической геометрии. – М.: Факториал пресс, 2000, – 208 с.

3. Шнейдер В.Е. и др. Краткий курс высшей математики. – М.: Высшая школа, 1998.

4. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.

5. Шипачев В.С. Основы высшей математики. — М.: Высшая школа,1998.

6. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989, – 659 с.

7. Фихтенгольц Г.М. Основы математического анализа. Часть 1. – М.: Лань, 2002, – 440 с.

Лекция 7

Эвклидово пространство

1. Понятие «эвклидово пространство»

Видео:Полная система векторовСкачать

01.10. Полные системы векторов

Если в пространстве V существует конечный набор векторов такой что, ℒº V, то система векторов Называется полной системой в V, а пространство Называется конечномерным. Таким образом, система векторов E1, E2, …, EnÎV называется полной в V системой, т. е. если

Если в пространстве V не существует конечной полной системы (а полная существует всегда – например, множество всех векторов пространства V), то пространство V Называется бесконечномерным.

9°. Если полная в V Система векторов и Y ÎV, то <E1, E2, …, En, Y> – также полная система.

◀ Достаточно в линейных комбинациях коэффициент перед Y брать равным 0. ▶

= (b1 + bNA1) e1 + (b2 + bNA2) e2 + … + ( bN –1 + bNAN –1) en –1 что и требовалось доказать. ▶

Используя, основанный на теореме 10°, процесс «прополки» (выбрасывание векторов, являющихся линейными комбинациями других векторов системы) можно построить минимальный полный набор векторов в пространстве V.

Видео:Линейная зависимость и линейная независимость векторов.Скачать

Векторные пространства

При проведении научных и прикладных исследование часто создаются модели, в которых рассматриваются точки и/или векторы определенных пространств. Например, в моделях шифров на эллиптических кривых используются аффинные и проективные пространства. К проективным прибегают тогда, когда необходимо ускорить вычисления, так как в формулах манипулирования с точками эллиптической кривой выводимых в рамках проективного пространства отсутствует операция деления на координату, которую в случае аффинного пространства обойти не удается.

Операция деления как раз одна из самых «дорогих» операций. Дело в том, что в алгебраических полях, а соответственно и в группах операция деления вообще отсутствует и выход из положения (когда не делить нельзя) состоит в том, что операцию деления заменяют умножением, но умножают не на саму координату, а на обращенное ее значение. Из этого следует, что предварительно надо привлекать расширенный алгоритм Евклида НОД и кое что еще. Одним словом, не все так просто как изображают авторы большинства публикаций о ЕСС. Почти все, что по этой теме опубликовано и не только в Интернете мне знакомо. Мало того, что авторы не компетентны и занимаются профанацией, оценщики этих публикаций плюсуют авторов в комментариях, т. е. не видят ни пробелов, ни явных ошибок. Про нормальную же статью пишут, что она уже 100500-я и от нее нулевой эффект. Так все пока на Хабре устроено, анализ публикаций делается огромный, но не качества содержания. Здесь возразить нечего — реклама двигатель бизнеса.

Линейное векторное пространство

Изучение и описание явлений окружающего мира с необходимостью приводит нас к введению и использованию ряда понятий таких как точки, числа, пространства, прямые линии, плоскости, системы координат, векторы, множества и др.

Пусть r = вектор трехмерного пространства, задает положение одной частицы (точки) относительно начала координат. Если рассматривать N элементов, то описание их положения требует задания 3∙N координат, которые можно рассматривать как координаты некоторого вектора в 3N-мерном пространстве. Если рассматривать непрерывные функции и их совокупности, то приходим к пространствам, размерность которых равна бесконечности. На практике часто ограничиваются использованием лишь подпространства такого бесконечномерного пространства функции координат, обладающего конечным числом измерений.

Пример 1. Ряд Фурье — пример использования пространства функций. Рассмотрим разложение произвольной функции в ряд Фурье

Его можно трактовать как разложение «вектора» f(x) по бесконечному набору «ортогональных» базисных векторов sinпх

Это пример абстрагирования и распространения понятия вектора на бесконечное число измерений. Действительно, известно, что при -π≤x≤π

Существо дальнейшего рассмотрения не пострадает, если мы отвлечемся от размерности абстрактного векторного пространства – будь — то 3, 3N или бесконечность, хотя для практических приложений больший интерес представляет конечномерные поля и векторные пространства.

Набор векторов r1, r2,… будем называть линейным векторным пространством L, если сумма любых двух его элементов тоже находится в этом наборе и если результат умножения элемента на число С также входит в этот набор. Оговоримся сразу, что значения числа С могут быть выбраны из вполне определенного числового множества Fр – поля вычетов по модулю простого числа р, которое считается присоединенным к L.

Пример 2. Набор из 8 векторов, составленных из n =5 -разрядных двоичных чисел
r0 = 00000, r1 = 10101, r2 = 01111, r3 = 11010, r4 = 00101, r5 = 10110, r6 = 01001, r7 = 11100 образует векторное пространство L, если числа С є . Этот небольшой пример позволяет убедиться в проявлении свойств векторного пространства, включенных в его определение.

Суммирование этих векторов выполняется поразрядно по модулю два, т. е. без переноса единиц в старший разряд. Отметим, что если все С действительные (в общем случае С принадлежат полю комплексных чисел), то векторное пространство называют действительным.

Формально аксиомы векторного пространства и записываются так:
r1 + r2 = r2 + r1 = r3; r1, r2, r3 є L – коммутативность сложения и замкнутость;
(r1 + r2) + r3 = r1 + (r2 + r3) = r1 + r2 + r3 – ассоциативность сложения;
ri + r0 = r0 + ri = ri; ∀i, ri, r0 є L–существование нейтрального элемента;
ri +(- ri) = r0, для ∀i существует противоположный вектор (-ri) є L;
1∙ ri = ri ∙1 = ri существование единицы для умножения;
α (β∙ri) = (α∙β)∙ri; α, β, 1, 0 – элементы числового поля F, ri є L; умножение на скаляры ассоциативно; результат умножения принадлежит L;
(α + β) ri = α∙ri + β∙ri; для ∀i, ri є L, α, β – скаляры;
а (ri + rj) = ari + arj для всех а, ri, rj є L;
a∙0 = 0, 0∙ri = 0; (-1) ∙ ri = – ri.

Размерность и базис векторного пространства

При изучении векторных пространств представляет интерес выяснение таких вопросов, как число векторов, образующих все пространство; какова размерность пространства; какой наименьший набор векторов путем применения к нему операции суммирования и умножения на число позволяет сформировать все векторы пространства? Эти вопросы основополагающие и их нельзя обойти стороной, так как без ответов на них утрачивается ясность восприятия всего остального, что составляет теорию векторных пространств.

Оказалось, что размерность пространства самым тесным образом связана с линейной зависимостью векторов, и с числом линейно независимых векторов, которые можно выбирать в изучаемом пространстве многими способами.

Линейная независимость векторов

Набор векторов r1, r2, r3 … rр из L называют линейно независимым, если для них соотношение

выполняется только при условии одновременного равенства .
Все , k = 1(1)p, принадлежат числовому полю вычетов по модулю два
F = .
Если в некотором векторном пространстве L можно подобрать набор из р векторов, для которых соотношение выполняется, при условии, что не все одновременно, т.е. в поле вычетов оказалось возможным выбрать набор , k =1(1)р, среди которых есть ненулевые, то такие векторы называются линейно зависимыми.

Пример 3. На плоскости два вектора = T и = T являются линейно независимыми, так как в соотношении (T-транспонирование)

невозможно подобрать никакой пары чисел коэффициентов не равных нулю одновременно, чтобы соотношение было выполнено.
Три вектора = T , = T , = T образуют систему линейно зависимых векторов, так как в соотношении

равенство может быть обеспечено выбором коэффициентов , не равных нулю одновременно. Более того, вектор является функцией и (их суммой), что указывает на зависимость от и . Доказательство общего случая состоит в следующем.

Пусть хотя бы одно из значений , k = 1(1)р, например, , а соотношение выполнено. Это означает, что векторы , k = 1(1)р, линейно зависимы

Выделим явным образом из суммы вектор r_р

Говорят, что вектор r_р является л и н е й н о й комбинацией векторов или r_р через остальные векторы выражается линейным образом, т.е. r_р линейно зависит от остальных. Он является их функцией.

На плоскости двух измерений любые три вектора линейно зависимы, но любые два неколлинеарных вектора являются независимыми. В трехмерном пространстве любые три некомпланарных вектора линейно независимы, но любые четыре вектора всегда линейно зависимы.

Зависимость/независимость совокупности <> векторов часто определяют, вычисляя определитель матрицы Грама (ее строки скалярные произведения наших векторов). Если определитель равен нулю, среди векторов имеются зависимые, если определитель отличен от нуля — векторы в матрице независимы.

Определителем Грама (грамианом) системы векторов

в евклидовом пространстве называется определитель матрицы Грама этой системы:

где — скалярное произведение векторов
и .

Размерность и базис векторного пространства

Размерность s = d (L) пространства L определяется как наибольшее число векторов в L, образующих линейно независимый набор. Размерность – это не число векторов в L, которое может быть бесконечным и не число компонентов вектора.

Пространства, имеющие конечную размерность s ≠ ∞, называются конечномерными, если
s = ∞, – бесконечномерными.

Ответом на вопрос о минимальном числе и составе векторов, которые обеспечивают порождение всех векторов линейного векторного пространства является следующее утверждение.

Любой набор s линейно независимых векторов в пространстве L образует его б а з и с. Это следует из того, что любой вектор линейного s-мерного векторного пространства L может быть представлен единственным способом в виде линейной комбинации векторов базиса.

Зафиксируем и обозначим символом , i = 1(1)s, один из наборов, образующих базис пространства L. Тогда

Числа r_ki, i = 1(1)s называются координатами вектора в базисе , i = 1(1)s, причем r_ki = (, ).
Покажем единственность представления . Очевидно, что набор , является зависимым, так как , i = 1(1)s – базис. Другими словами, существуют такие не равные одновременно нулю, что .
При этом пусть , ибо если , то хоть одно из , было бы отлично от нуля и тогда векторы , i = 1(1)s, были бы линейно зависимы, что невозможно, так как это базис. Следовательно,

, будем иметь
Используя прием доказательства «от противного», допустим, что записанное представление не единственное в этом базисе и существует другое

Тогда запишем отличие представлений, что, естественно, выражается как

Очевидно, что правая и левая части равны, но левая представляет разность вектора с самим собой, т. е. равна нулю. Следовательно, и правая часть равна нулю. Векторы , i = 1(1)s линейно независимы, поэтому все коэффициенты при них могут быть только нулевыми. Отсюда получаем, что

а это возможно только при

Выбор базиса. Ортонормированность

Векторы называют нормированными, если длина каждого из них равна единице. Этого можно достичь, применяя к произвольным векторам процедуру нормировки.

Векторы называют ортогональными, если они перпендикулярны друг другу. Такие векторы могут быть получены применением к каждому из них процедуры ортогонализации. Если для совокупности векторов выполняются оба свойства, то векторы называются ортонормированными.

Необходимость рассмотрения ортонормированных базисов вызвана потребностями использования быстрых преобразований как одно –, так и многомерных функций. Задачи такой обработки возникают при исследовании кодов, кодирующих информационные сообщения в сетях связи различного назначения, при исследовании изображений, получаемых
посредством автоматических и автоматизированных устройств, в ряде других областей, использующих цифровые представления информации.

Определение. Совокупность n линейно независимых векторов n-мерного векторного
пространства V называется его базисом.

Теорема. Каждый вектор х линейного n-мерного векторного пространства V можно представить, притом единственным образом, в виде линейной комбинации векторов базиса. Векторное пространство V над полем F обладает следующими свойствами:
0·х = 0 (0 в левой части равенства – нейтральный элемент аддитивной группы поля F; 0 в правой части равенства – элемент пространства V, являющийся нейтральным единичным элементом аддитивной группы V, называемый нулевым вектором);
(– 1)·х = –х; –1є F; x є V; –x є V;
Если α·х = 0єV, то при х ≠ 0 всегда α = 0.
Пусть Vn(F) – множество всех последовательностей (х1, х2, …, хn) длины n с компонентами из поля F, т.е. Vn(F) = <x, таких, что х = (х1, х2, …, хn), хi є F;
i =1(1)n >.

Сложение и умножение на скаляр определяются следующим образом:
x + y =(x1 + y1, x2 + y2, …, xn + yn);
α·х = (α·х1, α·х2,…, α·хn), где у = (у1, у2,…, уn),
тогда Vn(F) является векторным пространством над полем F.

Пример 4. В векторном пространстве rо = 00000, r1 = 10101, r2 = 11010, r3 = 10101 над полем F2 = определить его размерность и базис.
Решение. Сформируем таблицу сложения векторов линейного векторного пространства

В этом векторном пространстве V= каждый вектор в качестве противоположного имеет самого себя. Любые два вектора, исключая rо, являются линейно независимыми, в чем легко убедиться
c1·r1 + c2·r2 = 0; c1·r1 + c3·r3 = 0; c2·r2 + c3·r3 = 0;

Каждое из трех соотношений справедливо только при одновременных нулевых значениях пар коэффициентов сi, сj є .

При одновременном рассмотрении трех ненулевых векторов один из них всегда является суммой двух других или равен самому себе, а r1+r2+r3=rо.

Таким образом, размерность рассматриваемого линейного векторного пространства равна двум s = 2, d(L) = s = 2, хотя каждый из векторов имеет пять компонентов. Базисом пространства является набор (r1, r2). Можно в качестве базиса использовать пару (r1, r3).

Важным в теоретическом и практическом отношении является вопрос описания векторного пространства. Оказывается, любое множество базисных векторов можно рассматривать как строки некоторой матрицы G, называемой порождающей матрицей векторного пространства. Любой вектор этого пространства может быть представлен как линейная комбинация строк матрицы G ( как, например, здесь).

Если размерность векторного пространства равна k и равна числу строк матрицы G, рангу матрицы G, то очевидно, существует k коэффициентов с q различными значениями для порождения всех возможных линейных комбинаций строк матрицы. При этом векторное пространство L содержит q k векторов.

Множество всех векторов из ℤpn с операциями сложения векторов и умножения вектора на скаляр из ℤp есть линейное векторное пространство.

Определение. Подмножество W векторного пространства V, удовлетворяющее условиям:
Если w1, w2 є W, то w1+ w2 є W,
Для любых α є F и w є W элемент αw є W,
само является векторным пространством над полем F и называется подпространством векторного пространства V.

Пусть V есть векторное пространство над полем F и множество W ⊆ V. Множество W есть подпространство пространства V, если W по отношению к линейным операциям, определенным в V, есть линейное векторное пространство.

Таблица. Характеристики векторных пространств

Компактность матричного представления векторного пространства очевидна. Например, задание L векторов двоичных 50-разрядных чисел, среди которых 30 векторов образуют базис векторного пространства, требует формирования матрицы G[30,50], а описываемое количество векторов превышает 10 9 , что в поэлементной записи представляется неразумным.

Все базисы любого пространства L разбиваются подгруппой Р невырожденных матриц с det G > 0 на два класса. Один из них (произвольно) называют классом с положительно ориентированными базисами (правыми), другой класс содержит левые базисы.

В этом случае говорят, что в пространстве задана ориентация. После этого любой базис представляет собой упорядоченный набор векторов.

Если нумерацию двух векторов изменить в правом базисе, то базис станет левым. Это связано с тем, что в матрице G поменяются местами две строки, следовательно, определитель detG изменит знак.

Норма и скалярное произведение векторов

После того как решены вопросы о нахождении базиса линейного векторного пространства, о порождении всех элементов этого пространства и о представлении любого элемента и самого векторного пространства через базисные векторы, можно поставить задачу об измерении в этом пространстве расстояний между элементами, углов между векторами, значений компонентов векторов, длины самих векторов.

Действительное или комплексное векторное пространство L называется нормированным векторным пространством, если каждый вектор r в нем может быть сопоставлен действительному числу || r || – модулю вектора, норме. Единичный вектор – это вектор, норма которого равна единице. Нулевой вектор имеет компонентами нули.

Определение. Векторное пространство называется унитарным, если в нем определена бинарная операция, ставящая каждой паре ri, rj векторов из L в соответствие скаляр. В круглых скобках (ri, rj) записывается (обозначается) скалярное или внутреннее произведение ri и rj, причем
1. (ri, rj) = ri ∙ rj;
2. (ri, rj) = (rj ∙ ri)*, где * указывает на комплексное сопряжение или эрмитову симметрию;
3. (сri, rj) = с(ri ∙ rj) – ассоциативный закон;
4. (ri + rj, rk) = (ri ∙ rk)+ (rj ∙ rk)– дистрибутивный закон;
5. (ri, rk) ≥ 0 и из (ri, rj ) = 0 следует ri = 0.

Определение. Положительное значение квадратного корня называют нормой (или длиной, модулем) вектора ri. Если = 1, то вектор ri называют нормированным.

Два вектора ri, rj унитарного векторного пространства L взаимно ортогональны, если их скалярное произведение равно нулю, т.е. (ri, rj) = 0.

При s = 3 в линейном векторном пространстве в качестве базиса удобно выбирать три взаимно перпендикулярных вектора. Такой выбор существенно упрощает ряд зависимостей и вычислений. Этот же принцип ортогональности используется при выборе базиса в пространствах и других размерностей s > 3. Использование введенной операции скалярного произведения векторов обеспечивает возможность такого выбора.

Еще большие преимущества достигаются при выборе в качестве базиса векторного пространства ортогональных нормированных векторов – ортонормированного базиса. Если не оговорено специально, то далее всегда будем считать, что базис еi, i = 1(1)s выбран именно таким образом, т.е.

, где ij — символ Кронекера (1823 — 1891).

В унитарных векторных пространствах такой выбор всегда реализуем. Покажем реализуемость такого выбора.

Определение. Пусть S = есть конечное подмножество векторного пространства V над полем F.
Линейная комбинация векторов из S есть выражение вида а1∙v1 + а2∙v2 +…+ аn∙vn, где каждое аi ∊ F.

Оболочка для множества S (обозначение ) есть множество всех линейных комбинаций векторов из S. Оболочка для S есть подпространство пространства V.

Если U есть пространство в V, то U натянуто на S (S стягивает U), если =U.
Множество векторов S линейно зависимо над F, если в F существуют скаляры а1, а2,…, аn, не все нули, для которых а1∙v1+ а2∙v2 +…+ аn∙vn = 0. Если таких скаляров не существует, то множество векторов S линейно независимо над F.

Если векторное пространство V натянуто на линейно независимую систему векторов S (или система S стягивает пространство V), то система S называется базисом для V.

Приведение произвольного базиса к ортонормированному виду

Известно следующее утверждение [11]. Если ē _i, i = 1(1)s – произвольная конечная или счетная система линейно независимых векторов в унитарном векторном пространстве, то существует ортонормированная система ē _i, i = 1(1)s, порождающая то же самое линейное пространство (многообразие).

В основу процедуры приведения базиса к ортонормированному виду положен процесс ортогонализации Грама — Шмидта, который в свою очередь, реализуется рекуррентными формулами

В развернутом виде алгоритм ортогонализации и нормирования базиса содержит следующие условия:

Делим вектор ē ₁, на его норму; получим нормированный вектор ē _i=ē ₁/(||ē ₁ ||);
Формируем V2 = ē ₂ — (ē ₁, ē ₂)e ₁ и нормируем его, получим е ₂. Ясно, что тогда
(е1, е2)

(е1, е2) – (е1, ē ₂)( е1, е1) = 0;
Построив V3 = ē ₃– (e1, ē ₃)e1 – (e2, ē ₃) e2 и нормируя его, получим е3.

Для него имеем сразу же (е1, е3) = (е2, е3) = 0.
Продолжая такой процесс, получим ортонормированный набор ē _i, i = 1(1)s. Этот набор содержит линейно независимые векторы, поскольку все они взаимно ортогональны.
Убедимся в этом. Пусть выполняется соотношение

Если набор ē _i, i = 1(1)s зависимый, то хотя бы один сj коэффициент не равен нулю сj ≠ 0.

Умножив обе части соотношения на еj, получаем
(ej, c1∙e1 ) + (ej, c2∙e2 )+ . + ( ej, cj∙ej ) +…+ ( ej, cs∙rs ) = 0.
Каждое слагаемое в сумме равно нулю как скалярное произведение ортогональных векторов, кроме (ej ,cj∙ej), которое равно нулю по условию. Но в этом слагаемом
(ej, ej) = 1 ≠ 0, следовательно, нулем может быть только cj.
Таким образом, допущение о том, что cj ≠ 0 неверно и набор является линейно независимым.

Пример 5. Задан базис 3-х мерного векторного пространства:
.
Скалярное произведение определено соотношением:
( , ) = x1∙y1+x2∙y2+x3∙y3+x4∙y4.
Процедурой ортогонализации Грама — Шмидта получаем систему векторов:
а1 = ; a2 = -4 /7= /7;
a3 = +½ — /5 = /10.
(a1,a2)= (1+4+9+0) = 14;
a1 E =a1/√14;
a2-(a1 E ,a2)∙a1 E =a2-(8/√14)(a1/√14)=a2 — 4∙a1/7;
Третий вектор читателю предлагается обработать самостоятельно.

Нормированные векторы получают вид:
a1 E =a1/√14;
a2 E = /√70;
a3 E = /√70;

Ниже в примере 6 дается подробный развернутый процесс вычислений получения ортонормированного базиса из простого (взятого наугад).

Пример 6. Привести заданный базис линейного векторного пространства к ортонормированному виду.
Дано: векторы базиса

Подпространства векторных пространств

Структура векторного пространства

Представление объектов (тел) в многомерных пространствах весьма непростая задача. Так, четырехмерный куб в качестве своих граней имеет обычные трехмерные кубы, и в трехмерном пространстве может быть построена развертка четырехмерного куба. В некоторой степени «образность» и наглядность объекта или его частей способствует более успешному его изучению.

Сказанное позволяет предположить, что векторные пространства можно некоторым образом расчленять, выделять в них части, называемые подпространствами. Очевидно, что рассмотрение многомерных и тем более бесконечномерных пространств и объектов в них лишает нас наглядности представлений, что весьма затрудняет исследование объектов в таких
пространствах. Даже, казалось бы, такие простые вопросы, как количественные характеристики элементов многогранников (число вершин, ребер, граней, и т. п.) в этих пространствах решены далеко не полностью.

Конструктивный путь изучения подобных объектов состоит в выделении их элементов (например, ребер, граней) и описании их в пространствах меньшей размерности. Так четырехмерный куб в качестве своих граней имеет обычные трехмерные кубы и в трехмерном пространстве может быть построена развертка четырехмерного куба. В некоторой степени
«образность» и наглядность объекта или его частей способствует более успешному их изучению.

Если L – расширение поля К, то L можно рассматривать как векторное (или линейное) пространство над полем К. Элементы поля L (т. е. векторы) образуют по сложению абелеву группу. Кроме того, каждый «вектор» а є L может быть умножен на «скаляр» r є K, и при этом произведение ra снова принадлежит L (здесь ra – просто произведение в смысле операции поля L элементов r и а этого поля). Выполняются также законы
r∙(a+b) = r∙a+r∙b, (r+s)∙a = r∙a + r∙s, (r∙s)∙a = r∙(s∙a) и 1∙а = а, где r,s є K, a,b є L.

Сказанное позволяет предположить, что векторные пространства можно некоторым образом расчленять, выделять в них части, называемые подпространствами. Очевидно, что основным результатом при таком подходе является сокращение размерности выделяемых подпространств. Пусть в векторном линейном пространстве L выделены подпространства L1 и L2. В качестве базиса L1 выбирается меньший набор еi, i = 1(1)s1, s1 n – 1 способами. Следующий вектор v2 ≠ 0 не может быть выражен линейно через v1, т.е. может быть выбран q n – q способами и т.д.

Последний вектор vk ≠ 0 также линейно не выражается через предыдущие выбранные векторы v1,v2,…,vk и, следовательно, может быть выбран q n – q k – 1 способами. Общее число способов для выбора совокупности векторов v1,v2,…,vk, таким образом, определится как произведение числа выборов отдельных векторов, что и дает формулу (1). Для случая, когда k = п, имеем wп = wn, n и из формулы (I) получаем формулу (2).

Важные обобщающие результаты о размерностях подпространств.
Совокупность всех наборов длины n, ортогональных подпространству V1 наборов длины n, образует подпространство V2 наборов длины n. Это подпространство V2 называется нулевым пространством для V1.
Если вектор ортогонален каждому из векторов, порождающих подпространство V1, то этот вектор принадлежит нулевому пространству для V1.
Примером (V1) может служить множество 7-разрядных векторов порождающей матрицы (7,4)-кода Хемминга, с нулевым подпространством (V2) 7-разрядных векторов, образующих проверочную матрицу этого кода.

Если размерность подпространства (V1) наборов длины n равна k, то размерность нулевого подпространства (V2) равна n — k.

Если V2 — подпространство наборов длины n и V1 — нулевое пространство для V2, то (V2) — нулевое пространство для V1.

Пусть U∩V обозначает совокупность векторов, принадлежащих одновременно U и V, тогда U∩V является подпространством.

Пусть U⊕V обозначает подпространство, состоящее из совокупности всех линейных комбинаций вида au +bv, где u є U, v є V, a b — числа.

Сумма размерностей подпространств U∩V и U⊕V равна сумме размерностей подпространств U и V.

Пусть U2 — нулевое подпространство для U1, а V2 -нулевое пространство для V1. Тогда U2∩V2 является нулевым пространством для U1⊕V1.

Заключение

В работе рассмотрены основные понятия векторных пространств, которые часто используются при построении моделей анализа систем шифрования, кодирования и стеганографических, процессов, протекающих в них. Так в новом американском стандарте шифрования использованы пространства аффинные, а в цифровых подписях на эллиптических кривых и аффинные и
проективные (для ускорения обработки точек кривой).

Об этих пространствах в работе речь не идет (нельзя валить все в одну кучу, да и объем публикации я ограничиваю), но упоминания об этом сделаны не зря. Авторы, пишущие о средствах защиты, об алгоритмах шифров наивно полагают, что понимают детали описываемых явлений, но понимание евклидовых пространств и их свойств без всяких оговорок переносится в другие пространства, с другими свойствами и законами. Читающая аудитория вводится в заблуждение относительно простоты и доступности материала.

Создается ложная картина действительности в области информационной безопасности и специальной техники (технологий и математики).

В общем почин мною сделан, насколько удачно судить читателям.

📹 Видео

Линейная зависимость векторовСкачать

Разложение вектора по базису. 9 класс.Скачать

Что такое векторный базис? Душкин объяснитСкачать

Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Линейная зависимость векторов на примерахСкачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Образуют ли данные векторы базисСкачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Как разложить вектор по базису - bezbotvyСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Построение проекции вектора на осьСкачать

Примеры линейной зависимости векторов.Скачать

Линейные комбинации, span и базисные вектора | Сущность Линейной Алгебры, глава 2Скачать

Линейная зависимость и линейная независимость. ТемаСкачать

Базис. Разложение вектора по базису.Скачать

Примеры Линейная зависимость векторов Базис и ранг системы векторовСкачать

Линейная зависимость и независимость систем векторовСкачать