Есть ли у веса вектор (5 видео) | Курс школьной геометрии

Вес тела

Содержание

Содержание
Определение понятия веса тела
Характеристики веса
Вес как частный случай силы упругости
Что называют весом тела в физике
Вес тела — что это за сила в физике
Что такое точка опоры или подвеса
Графическое изображение, приборы для измерения
Формула нахождения веса тела в физике, примеры задач
Является ли вес скаляром или вектором?
🔍 Видео

Содержание

В предыдущих уроках мы узнали определение понятия силы, познакомились с силой тяжести и силой упругости.

Возможно, вы заметили, что рассматривая примеры и сравнивая тела с разными массами, мы избегали выражения “одно тело весит больше другого”. В повседневном жизни же мы часто используем подобные фразы, как и само слово “вес”.

В данном уроке мы узнаем о понятии веса со стороны физики.

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Определение понятия веса тела

Вспомним опыт, когда мы ставим тело (гирю) на опору (рисунок 1).

Рисунок 1. Деформация горизонтально расположенной доски, на которую поместили груз (гирю).

Мы уже говорили, что на гирю действует сила тяжести. Из-за этого начинает прогибаться доска — происходит ее деформация.

Возникает сила упругости, направленная вертикально вверх. Доска перестает прогибаться, когда сила тяжести и сила упругости уравновешивают друг друга.

Обратите внимание, что гиря и доска взаимодействуют друг с другом, но:

Cила тяжести — это результат взаимодействия гири с Землей, а не с доской
по всем изученным нами принципам должна быть еще одна сила, которая возникает со стороны гири

Подобная ситуация происходит в случае, если мы будем рассматривать тело, подвешенное на нити. Возникает некая сила, действующая на подвес.

Эта сила и называется весом тела.

Вес тела — это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.

Видео:Физика | Ликбез по векторамСкачать

Характеристики веса

Вес тела — это векторная физическая величина и обозначается буквой $vec
$
Модуль веса тела обозначается буквой $P$
Вес тела численно равен силе тяжести, если тело и опора/подвес неподвижны или движутся прямолинейно и равномерно, т.е.

Вес тела приложен к опоре или подвесу и направлен перпендикулярно опоре или вдоль подвеса (рисунки 2, 3).

Рисунок 2. Изображение веса тел. Рисунок 3. Изображение веса тела, лежащего на наклонной опоре.

Сравните с изображением силы тяжести (рисунок 4). Следует помнить, что сила тяжести приложена к самому телу.

Рисунок 4. Разница изображения силы тяжести и веса тела.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Вес как частный случай силы упругости

Когда мы ставим тело на опору — оно деформирует ее. Когда мы подвешиваем тело — оно деформирует подвес. Не всегда эта деформация видна как в наших предыдущих опытах.

Когда вы кладёте учебник на парту, что происходит? Учебник (тело) деформирует парту (опору). Но такая деформация не видна невооруженным глазом. Тем не менее, она существует. Если бы деформация не происходила, то не возникала бы сила упругости. Тогда ничего бы не препятствовало движению вашего учебника к самому центру Земли.

Так, парта в свою очередь деформирует учебник, что тоже незаметно.

Давайте рассмотрим опыт, где деформация тела будет заметна. Взгляните на рисунок 5.

Рисунок 5. Демонстрация деформации тела под действием подвеса и опоры.

У нас есть штатив и резиновый шнур длиной $l_0$ (рисунок 5, а). На шнур мы подвешиваем небольшой мешок с песком (рисунок 5, б).

Шнур растягивается и останавливается, когда сила тяжести становится равна возникшей в шнуре силе упругости. Длина шнура изменилась и стала равна $l$.

У нас провзаимодействовали два тела: шнур и мешок. Оба тела деформировались.

Теперь мы отрежем прикрепленный шнур (рисунок 5, в). Во время падения на мешок с песком действует только сила тяжести, он восстанавливает свою форму. Шнурок также восстанавливает свою форму.

Когда же мешок падает на рабочую поверхность (рисунок 5, г), то он снова деформируется. Теперь взаимодействует опора и тело.

В данном случае не видно, как деформируется опора, но, если бы мы подставили доску на брусьях, она бы прогнулась. Так мы наглядно показали, что при взаимодействии происходит деформация обоих тел.

Под действием опоры или подвеса происходит деформация тела. Опора сжимает нижнюю часть тела, а подвес растягивает его верхнюю часть.

Именно эта деформация тела вызывает появление в теле силы упругости. В данном случае сила упругости и будет весом тела.

Видео:Коллинеарность векторовСкачать

Что называют весом тела в физике

Видео:Физика с нуля. Вес и масса. Есть ли разница?Скачать

Вес тела — что это за сила в физике

Вес является силой, образованной в поле сил тяжести, с которой тело оказывает действие на опору, подвес, какое-либо крепление, препятствующее падению.

Обозначают вес тела с помощью буквы P. Единицами, в которых может выражаться вес тела, являются Ньютоны (Н).

Вышеизложенное определение веса тела принято в русскоязычной научной литературе. Кроме данной трактовки, в англоязычных источниках можно встретить краткий вариант понятия веса тела, обозначающий силу, с которой тело притягивается Землей.

В том случае, когда тело неподвижно относительно инерциальной системы отсчета, его вес P соответствует силе тяжести, которая приложена к рассматриваемому телу.

Величина веса тела прямо пропорциональна m и ускорению свободного падения g в заданной точке:

Можно заметить, что для расчета веса тела, которое находится в состоянии покоя, используется аналогичная формула, как для определения силы тяжести. Однако, данные понятия являются разными.

Величину ускорения свободного падения определяют следующие факторы:

высота над поверхностью Земли;
географические координаты точки, в которой производят измерения (так как планета не является сферической и вращается).

Таким образом, от данных условий зависит и вес тела. К примеру, в течение суток в процессе вращения планеты вес уменьшается по широте. По этой причине на экваторе величина на 0,3% меньше по сравнению с весом, измеряемым в районе полюсов.

Еще одним фактором, который влияет на g , является наличие гравитационных аномалий, обусловленных спецификой строения земной поверхности и недр в зоне, где измеряют показатель. При нахождении тела близко к поверхности другой планеты, а не Земли, величина ускорения свободного падения зависит от массы и габаритов рассматриваемой планеты, удаленности тела от ее поверхности.

В том случае, когда тело и опора или подвес передвигаются по отношению к инерциальной системе отсчета с ускорением w , вес тела будет отличаться от силы тяжести:

В качестве примера можно рассмотреть движение лифта. В том случае, когда ускорение (при любом значении скорости) лифта направлено вверх, вес объекта, который размещен в нем, возрастает. При направлении ускорения вниз, вес этого объекта будет уменьшаться.

Ускорение, возникающее, благодаря вращению планеты, не учтено в w . Данное ускорение входит в расчет g . Ситуацию, когда вес отсутствует, то есть невесомость, можно наблюдать при удалении от притягивающего объекта, либо в процессе свободного падения тела, то есть при:

К телу, обладающему массой m, чей вес требуется определить, могут быть приложены другие силы, которые косвенно можно объяснить наличием гравитации, включая силы Архимеда и трения.

К примеру, учитывая лишь действие силы тяжести тело, расположенное на наклонной плоскости и находящееся в состоянии покоя, обладает весом, который направлен по нормали к опоре:

где ( α ) является углом наклона.

При учете силы трения покоя, которая, согласно третьему закону Ньютона, действует на тело и на опору, вектор веса будет соответствовать:

Как и сила Архимеда, в жидкой или газообразной среде, плотность которой составляет ρ , к телу приложена подъемная сила:

где V — является обозначением объема тела.

В том случае, когда жидкая или газообразная среда играет роль опоры, согласно третьему закона Ньютона, с учетом воздействия со стороны тела силы Архимеда на жидкость, вектор веса будет соответствовать: m g

Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать

Что такое точка опоры или подвеса

Опора или подвес воспринимает действие внешних сил и/или моментов.

В точку опоры или подвеса приложены силы, которые оказывают воздействие на рассматриваемое тело. К примеру, на рисунке изображена балка на двух опорах. С левой стороны представлена неподвижная опора, а с правой — подвижная опора.

В зависимости от степени свободы, опоры бывают следующих видов:

Неподвижная (шарнирная) опора фиксирует положение элемента по трем степеням свободы. Отсутствует передача моментов. В том случае, когда опора неподвижна, можно наблюдать возникновение горизонтальных и вертикальных сил реакции опоры.

Подвижная опора удерживает элемент по одной или двум степеням свободы. Таким образом, объект может перемещаться по одному/двум направлениям. Передача моментов в этом случае отсутствует. Для подвижной опоры характерно формирование только вертикальных сил опоры.

Конструкции мостов в большинстве случаев имеют в основе по одной подвижной и одной неподвижной опоре. Таким образом, допускается восприятие теплового удлинения, и исключаются внутренние напряжения.

Защемление (заделка) служит барьером для перемещения по всем направлениям, в том числе вращения. Такая опора характеризуется передачей горизонтальных и вертикальных сил и моментов.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Графическое изображение, приборы для измерения

Вес является силой, с которой тело воздействует на опору или подвес. Графически изобразить действие веса можно таким образом:

С целью измерения веса тела используют пружинные весы. С помощью данного механизма, который проградуирован должным образом, можно получить косвенное значение массы. При использовании рычажных весов градуировка не требуется. Принцип их работы основан на сравнивании масс, которые находятся под действием одинакового ускорения свободного падения или суммы ускорений в неинерциальных системах отсчета.

Если взвешивание выполняют на технических пружинных весах, то значениями ускорения свободного падения чаще всего пренебрегают. Это объясняется тем, что данная величина меньше по сравнению с практически нужной точностью взвешивания.

В том случае, когда на тело действует сила Архимеда при его нахождении в жидкой или газообразной среде, вес может отличаться от аналогичного параметра, измеренного в условиях вакуума.

Видео:Урок 62. Сила тяжести и вес тела. Невесомость.Скачать

Формула нахождения веса тела в физике, примеры задач

Вес тела, которое находится в состоянии покоя:

Данная формула нашла широкое применение в решении задач по физике.

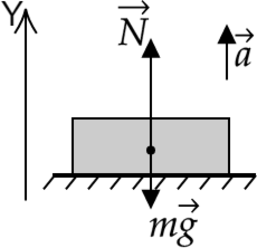
Объект обладает массой m. Он перемещается вместе с опорой с ускорением a, которое направлено вверх. Требуется определить вес тела.

Направление оси Y вертикально вверх можно представить с помощью рисунка:

Согласно второму закону Ньютона:

Проекция на ось Y:

N = mg + ma = m(g + a)

В результате, вес тела можно рассчитать по формуле:

Из формулы можно сделать вывод, что вес тела больше, чем сила тяжести. Данное состояние называют перегрузкой.

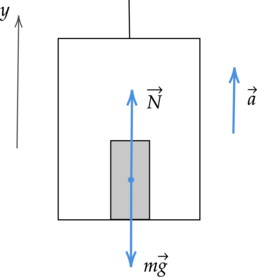
Масса тела равна m. Вместе с опорой тело перемещается, ускорение при этом составляет displaystyle a m a → = m g → + N →

Проекция на ось Y:

N = mg — ma = m(g — a)

Согласно записанной формуле, вес тела меньше по сравнению с силой тяжести. В том случае, когда displaystyle a=g, величина веса тела принимает нулевое значение. Описанное состояние называют невесомостью. В этом случае тело не оказывает воздействие на опору или подвес.

Имеются пять ящиков, которые являются одинаковыми, а их масса составляет 10 кг. Ящики разместили друг над другом на столе с горизонтальной поверхностью. Необходимо найти изменение (в Н) силы реакции опоры, которая приложена к первому ящику со стороны стола, при снятии трех верхних ящиков.

Вес тела представляет собой силу, с которой тело воздействует на опору или подвес. Согласно третьему закону Ньютона:

Равновесное положение достигается при условии:

Предположим, что масса одного ящика равна m. Можно выполнить замену 5 ящиков массой m на один большой ящик, масса которого также составляет 5m. В результате не произойдет изменения силы реакции опоры. Если убрать три ящика, масса груза составит 2m. Таким образом:

Δ P = 5 m g — 2 m g = 3 m g = 3 · 10 · 10 = 300 Н

Лифт движется вертикально вверх с ускорением 3 м/с^. В нем находится человек, масса которого составляет 70 кг. Необходимо вычислить вес человека в лифте (в Н).

Запись третьего закона Ньютона в модульной форме имеет вид:

Человек испытывает на себе действие двух сил:

N → , сила реакция напоры, которая направлена вверх;
сила тяжести m g → с направлением вниз.

Второй закон Ньютона можно записать таким образом:

m a → = N → + m g → ⇒ N = m ( a + g ) = 70 · 13 = 910 Н

Важно отметить справедливость перехода от векторной записи к скалярному выражению. Это объясняется действием всех приложенных к телу сил вдоль одной прямой (оси).

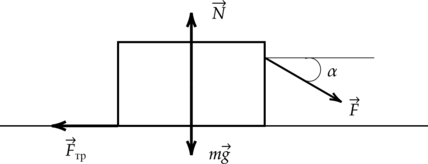
Ящик, масса которого равна 20 кг, перемещают равномерно по горизонтальной шероховатой поверхности. При этом сила, приложенная к ящику, направлена под определенным углом к горизонтали (сверху вниз). По модулю данная сила составляет 100 H. Ящик оказывает воздействие на поверхность с силой, по модулю равной 250 Н. Нужно определить величину угла между силой и горизонталью. Ответ необходимо выразить в градусах.

Проекция второго закона Ньютона на вертикаль:

0 = N — m g — F s i n α

В данном выражении N является силой воздействия ящика на поверхность, mg определяет силу тяжести, F выражает силу, приложенную к ящику. В результате, синус угла между силой и горизонталью равен:

s i n ( α ) = N — m g F = 250 H — 200 H 100 H = 0 , 5

Таким образом, угол ( α ) равен 30 ° .

Первая планета обладает сферической формой и радиусом 2000 км. Эта планета совершает равномерное вращательное движение относительно своей оси. Угловая скорость вращения планеты составляет 121 радиан в течение земных суток. Вторая планета также обладает сферической формой. Ее радиус составляет 3500 км. Данное космическое тело вращается вокруг своей оси с угловой скоростью 81 радиан в течение земных суток. Тела, которые расположены на экваторе обоих планет, пребывают в невесомости. Требуется определить отношение первого ускорения свободного падения ко второму. Ответ следует округлить до десятых долей.

Тела, расположенные на экваторе планеты, находятся в невесомости. Данный факт позволяет сделать вывод о том, что в районе экватора ускорение свободного падения обладает значением, аналогичным центростремительному ускорению. Отношение центростремительных ускорений можно записать таким образом:

ω 1 2 R 1 = ( 121 24 · 3600 ) 2 · 2 · 10 6 ≈ 3 , 9

Центростремительное ускорение второй планеты:

ω 2 2 R 2 = ( 81 24 · 3600 ) 2 · 3 , 5 · 10 6 ≈ 3 , 1

Тогда, ω определяет угловую скорость, R является радиусом планеты. Отношение центростремительных ускорений:

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Является ли вес скаляром или вектором?

Мой профессор утверждает, что вес является скаляром. Я отправил ему письмо, объясняющее, почему это вектор, я даже отправил ему источник из НАСА, который четко обозначил вес как вектор. Каждый другой источник также идентифицирует вес как вектор.

Я сказал, что вес — это сила, с mass умножает величину ускорение гравитации как скалярная величина и нисходящее направление.

Его ответ: «Вес не имеет направления, т. Е. Является скаляром . » Мой мыслительный процесс заключается в том, что поскольку вес является силой, а поскольку сила — вектор, вес должен быть вектором. Это основное транзитивное свойство равенства.

Я и все эти другие источники ошибочно относятся к тому, что вес является вектором? Является ли вес иногда вектором, а иногда и скаляром?

Прочитав его лекционные заметки, я обнаружил его аргументацию по его утверждению:

Аналогично тому, как скорость является скалярной величиной (или величиной) скорости, вес представляет собой скалярную величину (или величину) гравитационной силы, которую небесное тело оказывает на массу.

Я все еще склонен думать о весе как векторе для удобства и отделять его от повседневного языка. Однако, как и один из комментариев, «Определения служат нам».

На земле вес тела определяется как сила, с которой тело притягивается землей к ее центру. Вес можно считать таким же, как гравитационная сила , воздействующая на Землю на этом теле. Следовательно, вес можно считать vector , так как это сила, независимо от планеты, которую вы считаете. $$ vec W = m vec g = frac hat r $$ Как отмечалось в комментариях, поскольку $ g $ имеет одно и то же направление (направленное к центру соответствующей планеты), оно может быть (?) Считаться скаляром. То, что делает ваш профессор. Но, строго говоря, вес является вектором.

Надеюсь, это поможет вам.

Мы можем изменить определение вещей всякий раз, когда это полезно. Определения служат нам. Если определение не полезно, отдельные люди и сообщества меняют его, иногда «на лету», иногда в контексте, иногда явно, иногда неявно.

В повседневном опыте вес является скаляром. Вы не записываете направление веса бананов, которые вы покупаете. Настаивая на том, что это вектор, не полезен в этом контексте, а существуют определения как для выяснения связи, так и для решения проблем.

Добавляет ли направление к весу банана помощь в решении любых проблем? Или это шум? Является ли скалярный вес банана проблемой связи в этом случае?

Будут другие контексты, где вы хотите, чтобы вес был вектором; возможно, при расчете орбитальной механики вашего банана. Даже там вес не может быть полезной концепцией, потому что есть гораздо лучшие способы решения орбитальной механики, чем говорить о направленном весе вещей (например, полевые потенциалы).

В формальной математике очень конкретные и точные определения используются для разрешения абстракций, которые не соответствуют какой-либо физической ситуации, которая должна обсуждаться и делиться единообразным образом. Формальная математика часто разграблена физикой, но физика не является формальной математикой.

Физики и инженеры уйдут и расскажут о дельта-функциях дирака, значение которых 0 всюду, кроме 0, а интеграл от любого отрицательного значения до положительного — 1, а затем они свертывают его с другой функцией.

Теперь есть способы формализовать это, но по большей части физики и инженеры не утруждают себя . «Дельта Дирака не является функцией» полезна при ее оформлении, но не является как полезно, когда работает с ним . Знание формализации может быть полезно, чтобы избежать возможных ловушек, но обычно это не полезно при попытке использовать в качестве инструмента для прогнозирования поведения некоторой системы.

Физика — игра использования математики (или любого другого инструмента, удобного) для прогнозирования (а иногда и объяснения) поведения физических систем. Часто существует множество различных математических игр, и вы будете использовать разные для разных систем. Ньютоновская динамика — это игра, которая работает в своей области, и в ней скорость аддитивна. Относительность — игра, которая слишком сложна для некоторых доменов, но охватывает некоторую территорию, на которую не распространяется ньютоновская динамика; В теории относительности скорость не является аддитивной. В ньютоновской динамике скорость — простой вектор в евклидовом пространстве. Внутри Относительности это не простой вектор в евклидовом пространстве.

Вес — скаляр в некоторых играх физики. В других это может и не быть. В почти каждой разумной ситуации, которую вы испытаете, вес будет скалярным, потому что почти в каждой игре физики, где важно направление веса, использование векторного веса не будет лучшим инструментом, который у вас есть.