Построение сечений параллельных прямой или плоскости (8 видео)

Построение сечений параллельных прямой или плоскости

Правила построения сечений многогранников:

1) проводим прямые через точки, лежащие в одной плоскости;

2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого

а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);

б) параллельные грани плоскость сечения пересекает по параллельным прямым.

Примеры построения сечений:

Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Построим сечение, проходящее через точки M, N, L.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

Пересечем прямую ML ( принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

Найдем прямую пересечения плоскости сечения с плоскостью DD₁C₁C:

пересечем прямую ML (принадлежащую сечению) с ребром DD₁, они лежат в одной плоскости AA₁D₁D, получим точку X₂;

пересечем прямую KN (принадлежащую сечению) с ребром D₁C₁, они лежат в одной плоскости A₁B₁C₁D₁, получим точку X₃;

Точки X₂ и X₃ лежат в плоскости DD₁C₁C. Проведем прямую X₂ X₃ , которая пересечет ребро C₁C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.

MKNTPL — искомое сечение.

Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.

Соединим точки M и L, лежащие в плоскости AA₁D₁D.

Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.

Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее сточкой N, лежащей в этой же плоскости.

X₁ N пересекается с ребром A₁B₁ в точке К.

Соединим точки K и M, лежащие в одной плоскости AA₁B₁B.

Проведем прямую TP через точку T, параллельно прямой KM ( они лежат в параллельных плоскостях).

Соединим точки P и L ( они лежат в одной плоскости).

Содержание

Построение сечений многогранников с использованием свойств параллельности прямых и плоскостей в пространстве
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
Построение сечений
🌟 Видео

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Построение сечений многогранников с использованием свойств параллельности прямых и плоскостей в пространстве

Видео:№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Гл. I . Построение сечений многогранников на основе системы аксиом стереометрии…………………………………………………….

Гл. II . Метод следов в построении плоских сечений многогранников……………………………………………………………………..

Гл. III . Метод внутреннего проектирования в построении плоских сечений многогранников ……………………………………………………

Гл. IV . Комбинированный метод в построении плоских сечений многогранников……………………………………………….

В школы и вузы внедрена новая форма аттестации, и, следовательно, необходимо готовиться к ней. В них представлены задачи по геометрии по следующим характеристикам: уметь решать текстовую задачу, составляя математическую модель, предложенной в ней ситуации, уметь решать стереометрические задачи, уметь решать планиметрические задачи, уметь решать стереометрическую задачу на комбинацию геометрических тел. Так последнее содержит задание высокого уровня сложности и рассчитано на учащихся, планирующих в будущем связать свою профессиональную деятельность с углубленным изучением математики. Поэтому я хочу представить решение нескольких задач такого типа.

Мы строили плоские сечения многогранников лишь на основании аксиом и теорем стереометрии. Вместе с тем существуют определенные методы построения плоских сечений многогранников. Наиболее эффективными в школьном курсе геометрии являются следующие три метода:

метод внутреннего проектирования;

3)комбинированный метод.
Рассмотрим каждый из них на примерах.

Недостаточно специальной литературы, с помощью которой учащиеся могли бы решать задачи на построение сечений многогранников.

Систематизация основных теоретических знаний и классификация задач, включенных в ЕГЭ по геометрии на построение сечений.

Проанализировать решение задач на построение сечений несколькими методами;

1. Сделать подборку задач, предлагаемых различными центрами творческого образования в последние годы и проанализировать их решение;

2. Систематизировать задачи, привести их решения;

3. Выделить теоретические разделы математики, которые используются при решении данных заданий;

Методы работы: теоретический и практический анализ.

Построение сечений многогранников

на основе системы аксиом

Определение. Сечением многогранника плоскостью называется геометрическая фигура, представляющая собой множество всех точек пространства, принадлежащих одновременно данным многограннику и плоскости; плоскость при этом называется секущей плоскостью.

Поверхность многогранника состоит из ребер-отрезков и граней — плоских многоугольников. Так как прямая и плоскость пересекаются в точке, а две плоскости — по прямой, то сечением многогранника плоскостью является плоский многоугольник; вершинами этого многоугольника служат точки пересечения секущей плоскости с ребрами многогранника, а сторонами — отрезки, по которым секущая плоскость пересекает его грани. Это означает, что для построения искомого сечения данного многогранника плоскостью α достаточно построить точки ее пересечения с ребрами многогранника. Затем последовательно соединить отрезками эти точки, при этом выделить сплошными линиями, видимые и штриховыми — невидимые стороны полученного многоугольника — сечения (рис. 1-4).

Секущая плоскость α может быть задана: тремя точками, не лежащими на одной прямой; прямой и не принадлежащей ей точкой; другими условиями, определяющими ее положение относительно данного многогранника. Например, на рис. 1 построено сечение четырехугольной пирамиды РАВС D плоскостью α, заданной точками М, К и Н, принадлежащими ребрам соответственно РС, Р D и РВ; на рис. 2 секущая плоскость задана точками М, N и L , принадлежащими ребрам соответственно АА₁, В₁С₁ и А D куба

АВС D А₁ B ₁ C ₁ D ₁; на рис. 3 секущая плоскость проходит через вершину А основания АВС D перпендикулярно ребру РС правильной четырехугольной пирамиды РАВС D , высота РО которой образует угол в 30° с боковым ребром; на рис. 4 построено сечение куба АВСВА₁В₁С₁В₁ плоскостью, проходящей через его центр М перпендикулярно диагонали А₁С.

Эти сечения построены разными методами. Причем в двух первых случаях точки, определяющие секущую плоскость, могут быть любыми на ребрах многогранника, поэтому и секущая плоскость определена неоднозначно; в каждом из двух последних случаев секущая плоскость определяется однозначно метрическими свойствами многогранника и условиями расположения этой плоскости относительно данного многогранника. Но тем не менее во всех четырех случаях сечение каждого из многогранников строится по определенным правилам, с учетом аксиом стереометрии, аффинных и метрических свойств данного многогранника.

Примеры решения задач, используя аксиомы стереометрии.

Задача 1. Постройте сечение пирамиды РАВС плоскостью α = (МК H ), где М, К и Н— внутренние точки соответственно ребер РС, РВ и АВ (рис. 5, а).

Решение. 1-й шаг. Точки М и K лежат в каждой из двух плоскостей α и РВС. Поэтому по аксиоме пересечения двух плоскостей плоскость α пересекает плоскость РВС по прямой МК. Следовательно, отрезок МК — одна из сторон искомого сечения (рис. 5, б).

2-й шаг. Аналогично, отрезок КН — другая сторона искомого сечения (рис. 5, в).

3-й шаг. Точки М и Н не лежат одновременно ни в одной из граней пирамиды РАВС, поэтому отрезок МН не является стороной сечения этой пирамиды. Прямые КН и РА лежат в плоскости грани АВР и пересекаются. Построим точку T = КН ∩АР (рис. 5, г).

Поскольку прямая КН лежит в плоскости α, то и точка T лежит в плоскости α. Теперь мы видим, что плоскости α и АРС имеют общие точки М и T . Следовательно, по аксиоме пересечения двух плоскостей плоскость α и плоскость АРС пересекаются по прямой МТ, которая, в свою очередь, пересекает ребро АС в точке R (рис. 5, д).

4-й шаг. Теперь так же, как в шаге 1, устанавливаем, что плоскость α пересекает грани АСР и АВС по отрезкам MR и HR соответственно. Следовательно, искомое сечение — четырехугольник MKHR (рис.5,е).

■ Р

Задача 2. Постройте сечение пирамиды MABCD плоскостью α = (КНР), где K , H и P — внутренние точки ребер соответственно МА, МВ и MD (рис. 6, а).

Решение. Первые два шага аналогичны шагам 1 и 2 предыдущей задачи. В результате получим стороны КР и КН (рис. 6, б) искомого сечения. Построим остальные вершины и стороны многоугольника — сечения.

3-й шаг. Продолжим отрезок КР до пересечения с прямой AD в точке F (рис. 6, в). Так как прямая КР лежит в секущей плоскости α, то точка F = КР ∩ AD = КР ∩ (АВС) является общей для плоскостей α и АВС.

4-й шаг. Продолжим отрезок КН до пересечения с прямой АВ в точке L (рис. 6, г). Так как прямая КН лежит в секущей плоскости α, то точка L = КН ∩ АВ = КН ∩ (АВС) является общей для плоскостей α и АВС.

Таким образом, точки F и L являются общими для плоскостей α и АВС. Это означает, что плоскость α пересекает плоскость АВС основания пирамиды по прямой FL .

5-й шаг. Проведем прямую FL . Эта прямая пересекает ребра ВС и D С соответственно в точках R и T (рис. 6, д), которые служат вершинами искомого сечения. Значит, плоскость α пересекает грань основания ABCD по отрезку RT — стороне искомого сечения.

6-й шаг. Теперь проводим отрезки RH и РТ (рис. 6, е), по которым плоскость α пересекает грани ВМС и MCD данной пирамиды. Получаем пятиугольник РКН R Т — искомое сечение пирамиды MABCD (рис. 6, е).

Рассмотрим более сложную задачу.

Задача 3. Постройте сечение пятиугольной пирамиды PABCDE плоскостью α = ( KQR ), где K , Q — внутренние точки ребер соответственно РА и РС, а точка R лежит внутри грани DPE (рис. 7, а).

Решение. Прямые ( QK и АС лежат в одной плоскости АСР (по аксиоме прямой и плоскости) и пересекаются в некоторой точке T ₁, (рис. 7,б), при этом T ₁ є α, так как Q К є α .

Прямая Р R пересекает DE в некоторой точке F (рис. 7, в), которая является точкой пересечения плоскости АР R и стороны DE основания пирамиды. Тогда прямые К R и А F лежат в одной плоскости АР R и пересекаются в некоторой точке Т₂ (рис. 7, г), при этом Т₂ є α , как точка прямой KR є α (по аксиоме прямой и плоскости).

Получили: прямая Т₁ Т₂ лежит в секущей плоскости α и в плоскости основания пирамиды (по аксиоме прямой и плоскости), при этом прямая пересекает стороны DE и АЕ основания ABCDE пирамиды соответственно в точках М и N (рис. 7, д), которые являются точками пересечения плоскости α с ребрами DE и АЕ пирамиды и служат вершинами искомого сечения.

Далее, прямая MR лежит в плоскости грани DPE и в секущей плоскости α (по аксиоме прямой и плоскости), пересекая при этом ребро PD в некоторой точке Н — еще одной вершине искомого сечения (рис. 7, е).

Далее, построим точку Т₃ — Т₁Т₂ ∩ АВ (рис. 7, ж), которая, как точка прямой Т₁Т₂ є α, лежит в плоскости а (по аксиоме прямой и плоскости). Теперь плоскости грани РАВ принадлежат две точки Т₃ и К секущей плоскости α, значит, прямая Т₃К — прямая пересечения этих плоскостей. Прямая Т₃К пересекает ребро РВ в точке L (рис. 7, з), которая служит очередной вершиной искомого сечения.

Таким образом, «цепочка» последовательности построения искомого сечения такова:

1. Т ₁ = QK ∩ АС ; 2. F = PR ∩ DE;

5. N = Т ₁ Т ₂ ∩ АЕ ; 6. Н = MR ∩ PD;

Шестиугольник MNKLQH — искомое сече ние .

Замечание. Сечение пирамиды на рис. 1 и сечение куба на рис. 2 построены на основании лишь аксиом стереометрии.

Вместе с тем сечение многогранника, имеющего параллельные грани (призма, параллелепипед, куб), можно строить, используя свойства параллельных плоскостей.

Например, рассмотрим следующую задачу.

Задача 4. Точки M , P и R расположены на ребрах параллелепипеда (рис. 8). Пользуясь свойствами параллельных прямых и плоскостей, постройте сечение этого параллелепипеда плоскостью MPR .

Решение. Пусть точки M , P и R расположены на ребрах соответственно DD ₁, ВВ₁ и СС₁ 1 параллелепипеда АВСВА₁В₁С₁В₁ (рис. 8, а).

Обозначим: ( MPR ) = α — секущая плоскость. Проводим отрезки MR и PR (рис. 8, б), по которым плоскость α пересекает соответственно грани СС₁ D ₁ D и ВВ₁С₁С данного параллелепипеда. Отрезки MR и PR — стороны искомого сечения. Далее используем теоремы о пересечении двух параллельных плоскостей третьей.

Так как грань АА₁В₁В параллельна грани СС₁ D ₁ D , то прямая пересечения плоскости α с плоскостью грани АА₁В₁В должна быть параллельна прямой MR . Поэтому проводим отрезок PQ || MR , Q є АВ (рис. 8, в); отрезок Р Q — следующая сторона искомого сечения. Аналогично, так как грань АА₁ D ₁ D параллельна грани СС₁В₁В, то прямая пересечения плоскости α с плоскостью грани АА₁ D ₁ D должна быть параллельна прямой PR . Поэтому проводим отрезок МН || PR , H є AD (рис. 8, в); отрезок МН — еще одна сторона искомого сечения. На ребрах АВ и AD грани АВС D построили точки Q є АВ и H є AD , которые являются вершинами искомого сечения. Проводим отрезок QH (рис. 8, г) и получаем пятиугольник MRPQH — искомое сечение параллелепипеда. Штриховыми линиями проводим невидимые стороны MR , RP и QH этого сечения.

Замечание. При построении сечения куба на рис. 4 использованы параллельность противоположных граней куба, а также параллельность секущей плоскости и плоскости ВС₁ D .

Рис. 8

Видео:Построение сечений. Метод параллельных прямыхСкачать

Построение сечений

Определение

Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.

Замечание

Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию. Параллельность” и “Перпендикулярность. Углы и расстояния в пространстве”.

Важные определения

1. Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.

2. Две прямые в пространстве скрещиваются, если через них нельзя провести плоскость.

3. Прямая и плоскость параллельны, если они не имеют общих точек.

4. Две плоскости параллельны, если они не имеют общих точек.

5. Две прямые в пространстве называются перпендикулярными, если угол между ними равен (90^circ) .

6. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.

7. Две плоскости называются перпендикулярными, если угол между ними равен (90^circ) .

Важные аксиомы

1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Важные теоремы

1. Если прямая (a) , не лежащая в плоскости (pi) , параллельна некоторой прямой (p) , лежащей в плоскости (pi) , то она параллельна данной плоскости.

2. Пусть прямая (p) параллельна плоскости (mu) . Если плоскость (pi) проходит через прямую (p) и пересекает плоскость (mu) , то линия пересечения плоскостей (pi) и (mu) — прямая (m) — параллельна прямой (p) .

3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.

4. Если две параллельные плоскости (alpha) и (beta) пересечены третьей плоскостью (gamma) , то линии пересечения плоскостей также параллельны:

[alphaparallel beta, alphacap gamma=a, betacapgamma=b Longrightarrow aparallel b]

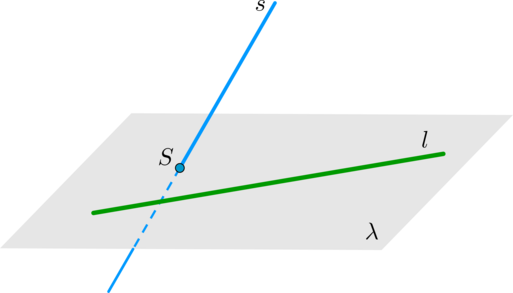
5. Пусть прямая (l) лежит в плоскости (lambda) . Если прямая (s) пересекает плоскость (lambda) в точке (S) , не лежащей на прямой (l) , то прямые (l) и (s) скрещиваются.

6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.

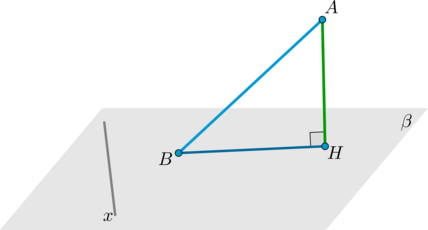
7. Теорема о трех перпендикулярах.

Пусть (AH) – перпендикуляр к плоскости (beta) . Пусть (AB, BH) – наклонная и ее проекция на плоскость (beta) . Тогда прямая (x) в плоскости (beta) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.

8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.

Замечание

Еще один важный факт, часто использующийся для построения сечений:

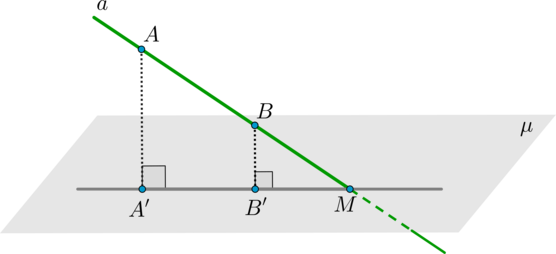
для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.

Для этого из двух произвольных точек (A) и (B) прямой (a) проведем перпендикуляры на плоскость (mu) – (AA’) и (BB’) (точки (A’, B’) называются проекциями точек (A,B) на плоскость). Тогда прямая (A’B’) – проекция прямой (a) на плоскость (mu) . Точка (M=acap A’B’) и есть точка пересечения прямой (a) и плоскости (mu) .

Причем заметим, что все точки (A, B, A’, B’, M) лежат в одной плоскости.

Пример 1.

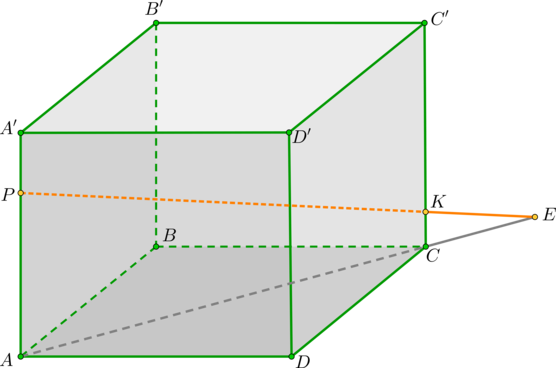
Дан куб (ABCDA’B’C’D’) . (A’P=dfrac 14AA’, KC=dfrac15 CC’) . Найдите точку пересечения прямой (PK) и плоскости (ABC) .

Решение

1) Т.к. ребра куба (AA’, CC’) перпендикулярны ((ABC)) , то точки (A) и (C) — проекции точек (P) и (K) . Тогда прямая (AC) – проекция прямой (PK) на плоскость (ABC) . Продлим отрезки (PK) и (AC) за точки (K) и (C) соответственно и получим точку пересечения прямых – точку (E) .

2) Найдем отношение (AC:EC) . (triangle PAEsim triangle KCE) по двум углам ( (angle A=angle C=90^circ, angle E) – общий), значит, [dfrac=dfrac]

Если обозначить ребро куба за (a) , то (PA=dfrac34a, KC=dfrac15a, AC=asqrt2) . Тогда:

Пример 2.

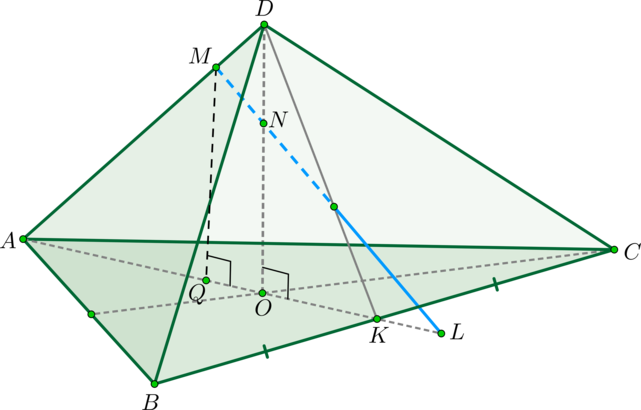
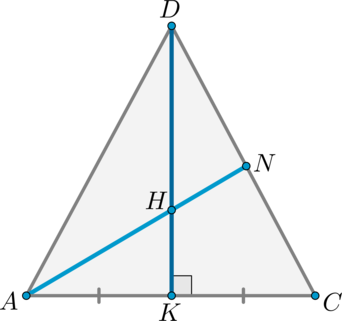
Дана правильная треугольная пирамида (DABC) с основанием (ABC) , высота которой равна стороне основания. Пусть точка (M) делит боковое ребро пирамиды в отношении (1:4) , считая от вершины пирамиды, а (N) – высоту пирамиды в отношении (1:2) , считая от вершины пирамиды. Найдите точку пересечения прямой (MN) с плоскостью (ABC) .

Решение

1) Пусть (DM:MA=1:4, DN:NO=1:2) (см. рисунок). Т.к. пирамида правильная, то высота падает в точку (O) пересечения медиан основания. Найдем проекцию прямой (MN) на плоскость (ABC) . Т.к. (DOperp (ABC)) , то и (NOperp (ABC)) . Значит, (O) – точка, принадлежащая этой проекции. Найдем вторую точку. Опустим перпендикуляр (MQ) из точки (M) на плоскость (ABC) . Точка (Q) будет лежать на медиане (AK) .
Действительно, т.к. (MQ) и (NO) перпендикулярны ((ABC)) , то они параллельны (значит, лежат в одной плоскости). Следовательно, т.к. точки (M, N, O) лежат в одной плоскости (ADK) , то и точка (Q) будет лежать в этой плоскости. Но еще (по построению) точка (Q) должна лежать в плоскости (ABC) , следовательно, она лежит на линии пересечения этих плоскостей, а это – (AK) .

Значит, прямая (AK) и есть проекция прямой (MN) на плоскость (ABC) . (L) – точка пересечения этих прямых.

2) Заметим, что для того, чтобы правильно нарисовать чертеж, необходимо найти точное положение точки (L) (например, на нашем чертеже точка (L) лежит вне отрезка (OK) , хотя она могла бы лежать и внутри него; а как правильно?).

Т.к. по условию сторона основания равна высоте пирамиды, то обозначим (AB=DO=a) . Тогда медиана (AK=dfrac2a) . Значит, (OK=dfrac13AK=dfrac 1a) . Найдем длину отрезка (OL) (тогда мы сможем понять, внутри или вне отрезка (OK) находится точка (L) : если (OL>OK) – то вне, иначе – внутри).

а) (triangle AMQsim triangle ADO) по двум углам ( (angle Q=angle O=90^circ, angle A) – общий). Значит,

[dfrac=dfrac=dfrac=dfrac 45 Rightarrow MQ=dfrac 45a, AQ=dfrac 45cdot dfrac 1a]

Значит, (QK=dfrac2a-dfrac 45cdot dfrac 1a=dfrac7a) .

б) Обозначим (KL=x) .
(triangle LMQsim triangle LNO) по двум углам ( (angle Q=angle O=90^circ, angle L) – общий). Значит,

Следовательно, (OL>OK) , значит, точка (L) действительно лежит вне отрезка (AK) .

Замечание

Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что (x) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки (L) (то есть, что она находится внутри отрезка (AK) ).

Пример 3

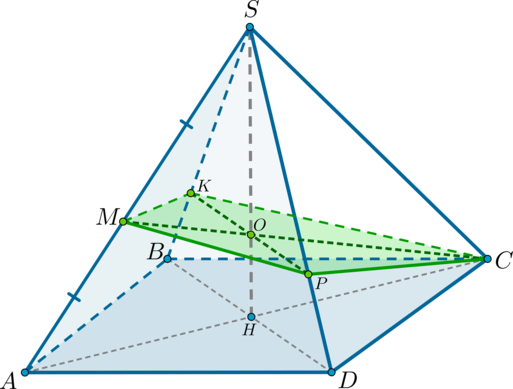
Дана правильная четырехугольная пирамида (SABCD) . Найдите сечение пирамиды плоскостью (alpha) , проходящей через точку (C) и середину ребра (SA) и параллельной прямой (BD) .

Решение

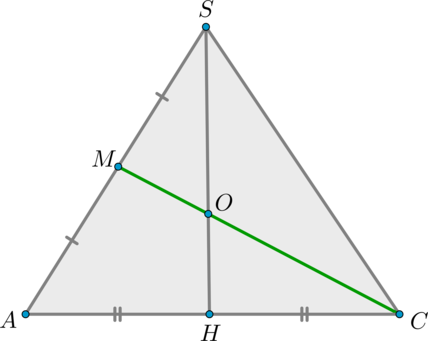
1) Обозначим середину ребра (SA) за (M) . Т.к. пирамида правильная, то высота (SH) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость (SAC) . Отрезки (CM) и (SH) лежат в этой плоскости, пусть они пересекаются в точке (O) .

Для того, чтобы плоскость (alpha) была параллельна прямой (BD) , она должна содержать некоторую прямую, параллельную (BD) . Точка (O) находится вместе с прямой (BD) в одной плоскости – в плоскости (BSD) . Проведем в этой плоскости через точку (O) прямую (KPparallel BD) ( (Kin SB, Pin SD) ). Тогда, соединив точки (C, P, M, K) , получим сечение пирамиды плоскостью (alpha) .

2) Найдем отношение, в котором делят точки (K) и (P) ребра (SB) и (SD) . Таким образом мы полностью определим построенное сечение.

Заметим, что так как (KPparallel BD) , то по теореме Фалеса (dfrac=dfrac) . Но (SB=SD) , значит и (SK=SP) . Таким образом, можно найти только (SP:PD) .

Рассмотрим (triangle ASC) . (CM, SH) – медианы в этом треугольнике, следовательно, точкой пересечения делятся в отношении (2:1) , считая от вершины, то есть (SO:OH=2:1) .

Теперь по теореме Фалеса из (triangle BSD) : (dfrac=dfrac=dfrac21) .

3) Заметим, что по теореме о трех перпендикулярах (COperp BD) как наклонная ( (OH) – перпендикуляр на плоскость (ABC) , (CHperp BD) – проекция). Значит, (COperp KP) . Таким образом, сечением является четырехугольник (CPMK) , диагонали которого взаимно перпендикулярны.

Пример 4

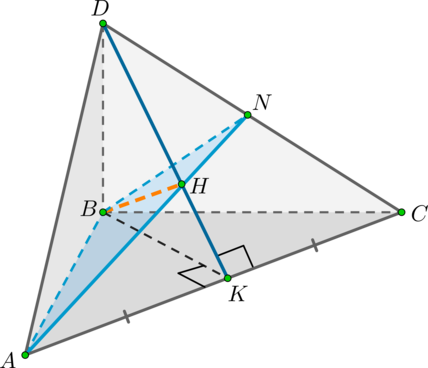
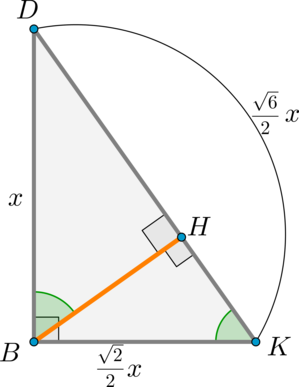
Дана прямоугольная пирамида (DABC) с ребром (DB) , перпендикулярным плоскости (ABC) . В основании лежит прямоугольный треугольник с (angle B=90^circ) , причем (AB=DB=CB) . Проведите через прямую (AB) плоскость, перпендикулярную грани (DAC) , и найдите сечение пирамиды этой плоскостью.

Решение

1) Плоскость (alpha) будет перпендикулярна грани (DAC) , если она будет содержать прямую, перпендикулярную (DAC) . Проведем из точки (B) перпендикуляр на плоскость (DAC) — (BH) , (Hin DAC) .

Проведем вспомогательные (BK) – медиану в (triangle ABC) и (DK) – медиану в (triangle DAC) .
Т.к. (AB=BC) , то (triangle ABC) – равнобедренный, значит, (BK) – высота, то есть (BKperp AC) .
Т.к. (AB=DB=CB) и (angle ABD=angle CBD=90^circ) , то (triangle ABD=triangle CBD) , следовательно, (AD=CD) , следовательно, (triangle DAC) – тоже равнобедренный и (DKperp AC) .

Применим теорему о трех перпендикулярах: (BH) – перпендикуляр на (DAC) ; наклонная (BKperp AC) , значит и проекция (HKperp AC) . Но мы уже определили, что (DKperp AC) . Таким образом, точка (H) лежит на отрезке (DK) .

Соединив точки (A) и (H) , получим отрезок (AN) , по которому плоскость (alpha) пересекается с гранью (DAC) . Тогда (triangle ABN) – искомое сечение пирамиды плоскостью (alpha) .

2) Определим точное положение точки (N) на ребре (DC) .

Обозначим (AB=CB=DB=x) . Тогда (BK) , как медиана, опущенная из вершины прямого угла в (triangle ABC) , равна (frac12 AC) , следовательно, (BK=frac12 cdot sqrt2 x) .

Рассмотрим (triangle BKD) . Найдем отношение (DH:HK) .

Заметим, что т.к. (BHperp (DAC)) , то (BH) перпендикулярно любой прямой из этой плоскости, значит, (BH) – высота в (triangle DBK) . Тогда (triangle DBHsim triangle DBK) , следовательно

[dfrac=dfrac Rightarrow DH=dfrac3x Rightarrow HK=dfrac6x Rightarrow DH:HK=2:1]

Рассмотрим теперь (triangle ADC) . Медианы треугольника точной пересечения делятся в отношении (2:1) , считая от вершины. Значит, (H) – точка пересечения медиан в (triangle ADC) (т.к. (DK) – медиана). То есть (AN) – тоже медиана, значит, (DN=NC) .