Укажите нарушенные правила и логические ошибки определений понятий:
квадрат — четырехугольник, у которого есть прямой угол
Определение неверно, т.к. оно не раскрывает содержание понятия. четырехугольник, у которого есть прямой угол может быть и трапеция и прямоугольник и любая фигура у которой есть четыре угла один из которых прямой.
Дадим наиболее полное определение квадрата:
квадрат — четырехугольник, у которого три прямых угла и все стороны равны
свет — это движение лучей, состоящих из светящихся телец
Определение неверно, т.к. оно не раскрывает содержание понятия. Лучей, состоящих из светящихся телец не существует.
Дадим наиболее полное определение квадрата:
Свет — электромагнитное излучение, испускаемое нагретым или находящимся в возбуждённом состоянии веществом, воспринимаемое человеческим глазом. Нередко, под светом понимают не только видимый свет, но и примыкающие к нему широкие области спектра.
музей — учреждение, изучающее предметы материальной культуры
Определение неверно, т.к. оно не раскрывает содержание понятия. музей занимается обширной деятельностью. Музей это учреждение с постоянным местом расположения, которое служит на благо развития общества, будучи открытым для публики. Музеи приобретают, сберегают, изучают экспонаты, проводят выставки и презентации с целью обучения, развлечения и духовного и материального насыщения человека
опиум вызывает сон, так как он содержит снотворную силу.
Это не определение понятия, т.к. содержание не раскрыто, что такое опиум не сказано, признаки входящие в его содержание не выявлены.
Эрмитаж не есть закрытое дворцовое собрание картин.
Определение понятия не раскрывает его содержание это не закрытое дворцовое собрание картин, а что это тогда: открытое дворцовое собрание картин и собрание картин ли это вообще, т.е. признаки входящие в его содержание не выявлены
Эрмитаж — это удивительный мир, полный чудес!
Это не определение понятия, т.к. содержание не раскрыто (удивительным миром, полным чудес можно назвать многое), о признаках входящие в его содержание вообще ничего не сказано.
музей — государственное учреждение
Определение понятия музей не полное, музеи могут быть и не государственными, признаки входящие в его содержание не выявлены. Гос. учреждений много и это не только музеи.
Эрмитаж — не Лувр
Определение понятия музей не полное, да Эрмитаж -это не Лувр, но что тогда, не Лувр многие предметы, не все же они Эрмитаж….
Видео:Синтаксические и логические ошибки в коде 1С: как находить и исправлятьСкачать

Конспект урока по ТОНКМ с МП по теме «Требования к определению математических понятий»
Видео:4 закона логики | Дмитрий ГусевСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»
Сертификат и скидка на обучение каждому участнику
Тема: Требования к определению понятий
Цель: добиться осознанного усвоения студентами требований, предъявляемых к определению математического понятия
Познакомиться с основными требованиями, предъявляемыми к определению математических понятий, учиться находить ошибки, допущенные в формулировке определения;
Развивать математическую речь, мышление, анализ, синтез, обобщение, классификацию;
Воспитывать познавательный интерес, коммуникативную культуру
Оборудование: учебные пособия по ТОНКМ (Л.П. Стойлова, А.М. Пышкало), математике (Л.П. Стойлова); раздаточный материал.
I . Организационный момент.
III . Открытие нового знания
Чтобы оценить правильность явных определений, надо знать правила определения понятий. Так как преобладающее большинство определений в школьном курсе математики — это определения через род и видовое отличие, то речь будет идти о правилах этих определений.
Прежде всего, определяемое и определяющее понятия должны быть соразмерны . Это значит, что совокупности предметов, охватываемые ими, должны совпадать. Соразмерны, например, понятия «прямоугольник» и «четырехугольник, в котором все углы прямые». Если же объем определяющего понятия включает в себя объем понятия определяемого, то говорят об ошибке слишком широкого определения. Так, определение «Прямые а и b называются параллельными, если они не имеют общих точек или совпадают» слишком широко, поскольку ему удовлетворяют и скрещивающиеся прямые. Если же объем определяющего понятия уже объема определяемого понятия, то имеет место ошибка слишком узкого определения. Например, определение «Прямые а и b называются параллельными, если они не имеют общих точек» слишком узко, поскольку ему не удовлетворяют совпадающие прямые.
Второе правило определения запрещает порочный круг : нельзя определять понятие через само себя или определять его через другое понятие, которое, в свою очередь, определяется через него. Возьмем такие понятия начальной математики, как «умножение» и «произведение», и дадим им следующие определения:
Умножением чисел называется действие, при помощи которого находят произведение этих чисел.
Произведением чисел называется результат их умножения.
Видим, что умножение определяется через понятие произведения, а произведение — через понятие умножения. Определения образовали, как говорят в математике, порочный круг. В результате цепочка последовательных определений, выстроенных в рамках курса, прерывается.
Порочный круг содержится и в таком определении: «Решением уравнения называется число, которое является его решением». Здесь Понятие «решение уравнения» определяется, по сути дела, через решение уравнения.
Третьим важным требованием к логически правильному определению понятия является следующее: в определении должны быть указаны все свойства, позволяющие однозначно выделять объекты, принадлежащие объему определяемого понятия .
Рассмотрим, например, такое определение Понятия «смежные углы»: «Смежными называются углы, которые в сумме составляют 180°». Нетрудно увидеть, что под данное определение можно подвести не только углы, изображенные на рисунке 2 и действительно являющиеся смежными, но и углы, изображенные на рисунке 3. Почему так произошло? Дело в том, что в приведенном определении смежных углов указано лишь одно их свойство, а именно свойство составлять в сумме 180°, но его недостаточно для выделения смежных углов из всех других.
Еще одно требование к правильному определению понятия — отсутствие в нем избыточности . Это означает, что в определении не должно быть указано лишних свойств, вытекающих из других свойств, также включенных в определение понятия.
Рассмотрим определение: «Прямоугольником называется четырехугольник, у которого противоположные стороны равны и все углы прямые». Можно показать, что включенное в определение свойство «иметь равные стороны» вытекает из свойства «иметь прямые углы». Следовательно, данное определение прямоугольника избыточное и правильнее определять прямоугольник таким образом: «Прямоугольником называется четырехугольник, у которого все углы прямые».
Следует сказать, что в любом определении понятия есть элемент произвола, что проявляется во-первых в выборе термина (прямоугольник в котором все стороны равны, мог бы называться и по-другому), а во-вторых, в выборе свойств, включаемых в определение. В принципе понятие квадрата можно определить так: «Квадратом называется ромб, у которого все углы прямые» – или так: «Квадратом называется параллелограмм, у которого все стороны равны, а углы прямые». Различные определения одного и того же понятия возможны потому, что из большого числа свойств, входящих в содержание этого понятия, в определение включаются только некоторые.
Если одному и тому же понятию даются, например, два различных определения, то они должны быть равносильными. Это означает, что из свойств, включенных в одно определение, должны вытекать свойства, положенные в основу другого определения, и наоборот.
Чем же руководствуются, когда из возможных определений некоторого понятия выбирают одно? Исходят из того, какое определение проще, естественнее или целесообразнее для дальнейшего построения теории.
Если же какие-либо свойства оказываются включенными в определение, то другие свойства тех же объектов могут быть логически выведены из тех, что вошли в определение. Это важное положение используют при решении задач на распознавание. Если объект А принадлежит объему определяемого понятия, то он обладает всеми свойствами, которые указаны в определении понятия. Справедливо и обратное утверждение, т. е. если известно, что объект А обладает всеми свойствами, которые указаны в он определении понятия, называемого некоторым термином, то и объект А можно назвать этим термином.
Пример. Используя определение диаметра окружности, установим, в каком из случаев, представленных на рисунке 4, отрезок CD является диаметром.
Определим диаметр окружности следующим образом: диаметром окружности называется хорда, проходящая через ее центр. Чтобы отрезок CD оказался диаметром окружности, достаточно одновременное выполнение двух условий: отрезок С D должен быть хордой окружности и проходить через ее центр. Этим двум условиям удовлетворяет отрезок С D в случае «а». В случае «б» отрезок С D — хорда, но он не проходит через центр окружности; в случае «в» отрезок С D проходит через центр окружности, но не является хордой.
Еще одним требованием к логически правильному определению понятия является следующее: необходимо, чтобы определяемый объект существовал . Рассмотрим, например, такое определение: «Тупоугольным треугольником называется треугольник, у которого все углы тупые». Нетрудно убедиться в том, что треугольник, у которого все углы тупые, не существует. Следовательно, данному определению реально ничего не соответствует, и поэтому оно не может считаться логически правильным.
Заметим, что в математике для ответа на вопрос, существует ли объект, удовлетворяющий данному определению, как правило, доказывают специальную теорему, подтверждающую возможность существования объекта, о котором говорится в определении. В геометрии существование объекта, удовлетворяющего определению, иногда обосновывают, построив его.
III . Первичное закрепление изученного материала
Найдите логические ошибки (если они есть) в следующих определениях и исправьте их.
1) Прямоугольником называется четырехугольник, у которого противоположные стороны равны;
2) Биссектрисой угла называется прямая, делящая угол пополам;
3) Сложение – это когда числа складываются;
4) Равносторонним треугольником называется треугольник, у которого все стороны и все углы равны;
5) Параллелограмм – это многоугольник, у которого противоположные стороны попарно параллельны;
6) Квадрат – это ромб с прямым углом;
7) Квадрат – это когда все стороны равны;
8) Прямоугольник – это параллелограмм с прямым углом;
9) Равные треугольники – это треугольники, которые равны.
10) Прямоугольник, у которого диагонали взаимно перпендикулярны, есть квадрат.
V . Подведение итогов урока
– Назовите основные требования, предъявляемые к определению математических понятий
V . Домашнее задание (с инструктажем)
Видео:Типичные ошибки оформления задач второй части. Профильный ЕГЭ. МатематикаСкачать

Выполнение заданий
Задание 1. Назовите по три понятий, принадлежащих объему понятий:
а) рациональное число б) четырехугольник в) математика г) мебель д)музыкальный национальный инструмент
тувинского народа е) часы
ж) специальности в колледже
e) предметы на 1 курсе
Задание 2. Укажите общие свойства следующих пар понятий:
a) трапеции и ромба; б) треугольника и параллелограмма;
в) прямоугольника и круга.
Задание 3. Определите, в каких отношениях находятся следующие понятия а, в, с и изобразите их объемы А, В, С на диаграммах Эйлера-Венна:
a) «прямая», «луч», «отрезок» б) «дерево», «растение», «кустарник»
b) «целое число», «натуральное число», «отрицательное число»
г) «треугольник», «многоугольник», «геометрическая фигура».
Задание 4. Для каждого из понятий укажите родовое понятие:
a) «кустарник», б) «квадрат», в) «стол», г) «нечетное число».
Задание 5. Для каждого из понятий укажите два видовых понятия:
a) «животное», б) «часть речи», в) «одежда», г) «параллелограмм».
Задание 6. Укажите три понятия, являющееся родовыми для понятия «прямоугольник». Какое из них ближайшее?
Задание 7. Приведите примеры разных определений из учебников математики начальных классов, разработанных по требованиям фгос ноо и выясните, к каким определениям они относятся.
Задание 8. Выясните с помощью
учебников математики начальных классов каким способом определяются в начальном курсе математики понятия:
а) «числовое выражение»; «однозначное число»;
в) «уменьшаемое»; г) «разность»; д) «площадь»; е) «квадрат».
Задание 9. Выясните, какие из определений верны (соразмерны):
a) Правильный треугольник
треугольник, у которого все стороны равны.
6) Остроугольный треугольник треугольник с острым углом.
Прямоугольник четырехугольник, у которого все углы прямые и смежные стороны равны.
Задание 10. Укажите логические ошибки, опустите лишние слова или добавьте нужные слова B следующих определениях:
a) Луч есть прямая, ограниченная с одной стороны.
6) Отрезком называется прямая, ограниченная с двух сторон.
b) Квадратом называется прямоугольник, диагонали которого равны и делят друг друга пополам.
г) Секущей называется бесконечная прямая, проходящая через какие- нибудь точки окружности.
Задание 11. Найдите ошибки в определениях, выясните тип ошибки:
a) Математика — это наука.
б) Дуб-это дерево, которое растет в лесу.
b) Прямая, делящая сторону треугольника пополам, называется медианой.
г) Сложением называется действие, при котором числа складываются.
Задание 12. Проверьте правильность следующих классификаций понятий:
a) понятие «треугольник» делится на понятия: «остроугольный треугольник», «прямоугольный треугольник», «тупоугольный треугольник», «равносторонний треугольник», «равнобедренный треугольник»;
6) под понятие «натуральное число» делится на понятия: «четное число», «нечетное число», «число, кратное на 3»;
b) понятие «четырехугольник» делится на понятия: «параллелограмм» и «трапеция».
B случае, если классификация выполнена неправильно, укажите какое условие нарушено и
Задание 13. Выполните правильные классификации следующих понятий:
Вуз, студент, угол, музыкальный инструмент, мебель, обувь, домашнее животное, домашняя птица, посуда, часы, учитель, здание, дерево, число, буква русского алфавита, множество, житель города.
Задание 14. Докажите, что понятие «четырехугольник» родовое по отношению к понятию «квадрат». В какой зависимости находятся содержания этих понятий?
💥 Видео
8 задание ЕГЭ // Грамматические ошибки в сложных предложениях // ЕГЭ Русский язык 2022Скачать

09-04 Ошибки 1 и 2 родаСкачать
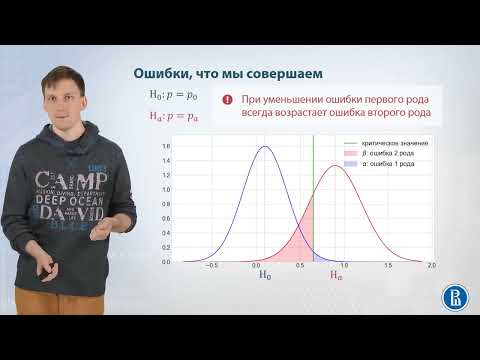
Логика. Основы Логики. Логическое МышлениеСкачать

Вся теория по четырехугольникам. Все прототипы №17 из ОГЭ-2024 по математике| РозыгрышСкачать

СУЖДЕНИЕ КАК ЛОГИЧЕСКАЯ ФОРМАСкачать

Формирование логических умений и оценка уровня их сформированности на уроках мСкачать
09-06 доска Ошибка 1 и 2 рода для настоящего критерияСкачать

Глава 1-7. Повторение. Учебник Логики. Георгий Челпанов.Скачать

Георгий Челпанов. Учебник логики. Главы 1-26 (Книга полностью)Скачать

Разбор ЕГЭ по Базовой Математике 2024. Вариант 1 Ященко. Куценко Иван. Онлайн школа EXAMhackСкачать

Задание 10 ЕГЭ по математике #4Скачать

Неизвестные логические операцииСкачать
Супер ЖЕСТЬ для продвинутых: sqrt(2+sqrt(2-sqrt(2+x)))=xСкачать

Возврат нескольких значений функции через указатели. Функция возвращает несколько значений. #49Скачать

Основы логики | КЛАДЕЗЬ ЗНАНИЙСкачать

Логика. 1. ПонятиеСкачать

Журнал событий: Как просмотреть информацию об ошибках, исправить ошибки в Windows 10, 8 или 7 💥📜💻Скачать



