Вектор d в электростатике

Вы будете перенаправлены на Автор24

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Что такое вектор электрической индукции

Вектором электрической индукции (или вектором электрического смещения) ($overrightarrow$) называют физическую величину, которая определяется в системе СИ как:

где $_0$ — электрическая постоянная, $overrightarrow$ — вектор напряженность, $overrightarrow

$ — вектор поляризации.

В СГС вектор электрического смещения определен как:

[overrightarrow=overrightarrow+4pi overrightarrow

left(2right).]

Вектор $overrightarrow$ не является чисто полевым вектором, так как он учитывает поляризованность среды. Этот вектор связан с объемной плотностью заряда соотношением:

Из (3) мы видим, что единственным источником $overrightarrow$ являются свободные заряды, на которых данный вектор начинается и заканчивается. В точках, где свободные заряды отсутствуют, вектор электрической индукции непрерывен. Изменение напряженности поля, которые вызваны наличием связанных зарядов, учитываются в самом векторе $overrightarrow$.

Видео:Билет №02 "Теорема Гаусса"Скачать

Связь вектора напряженности и вектора электрического смещения

Связь вектора напряженности и вектора электрического смещения, если среда изотропна, еще можно записать как:

[overrightarrow=left(_0overrightarrow+_0varkappa overrightarrowright)=left(_0+_0varkappa right)overrightarrow=varepsilon _0overrightarrowleft(4right),]

Использование вектора $overrightarrow$ существенно облегчает анализ поля при наличии диэлектрика. Так, например теорема Остроградского — Гаусса в интегральном виде при наличии диэлектрика может быть записана как:

При переходе через границу раздела двух диэлектриков для нормальной составляющей вектора $overrightarrow$ можно записать:

где $sigma $ — поверхностная плотность распределения зарядов на границе диэлектриков. $overrightarrow$ — нормаль, которая проведена в сторону второй среды.

Для тангенциальной составляющей:

Единицей измерения в системе СИ вектора электрической индукции служит $frac.$

Поле вектора $overrightarrow$ можно изображать с помощью линий электрического смещения. Направление и густота определяются аналогично линиям вектора напряженности. Однако в отличие от вектора $overrightarrow$ линии вектора электрической индукции начинаются и заканчиваются только на свободных зарядах.

Задание: Пластины плоского конденсатора имеют заряд q. Как изменится вектор электрической индукции, если пространство между пластинами сначала было заполнено воздухом, а за тем диэлектриком с диэлектрической проницаемостью $varepsilon ne _$.

Пусть поле в конденсаторе в первом случае характеризуется вектором смещения ($_=1$):

Заполним пространство между пластинами конденсатора однородным и изотропным диэлектриком. Под действием поля в конденсаторе диэлектрик поляризуется. На его поверхности появляются связанные заряды с плотностью ($_$). Они создают дополнительное поле, напряженность которого равна:

Векторы поля $overrightarrow$ и $overrightarrow$ направлены в противоположные стороны, при чем:

Результирующее поле в присутствии диэлектрика можно записать как:

Зная, что плотность связанных зарядов можно найти как:

Подставим (1.5) в (1.4), получим:

[E=E_1-varkappa E left(1.6right).]

Выразим из (1.6) напряженность поля E, получим:

Следовательно, вектор электрической индукции в диэлектрике равен:

Ответ: Вектор электрической индукции не изменится.

Готовые работы на аналогичную тему

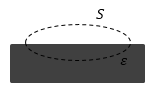
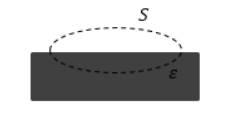
Задание: В зазор между разноименно заряженными пластинами внесли пластину из диэлектрика с диэлектрической проницаемостью $varepsilon$, которая не несет свободных зарядов. Штриховой линией на рисунке изображена замкнутая поверхность (рис.1). Чему равен поток вектора электрической индукции ($Ф_D$) через эту поверхность?

Поток вектора электрического смещения ($Ф_D$) через замкнутую поверхность $S$ равен:

С другой стороны по теореме Остроградского — Гаусса $Ф_D$ равен суммарному свободному заряду, который находится внутри заданной поверхности. По условию нашей задачи свободных зарядов в диэлектрике и в пространстве между пластинами конденсатора, которое не занято диэлектриком свободных зарядов нет, следовательно, поток вектора электрической индукции равен нулю.

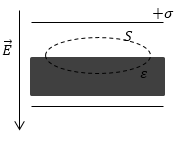
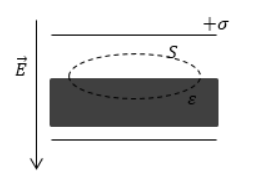
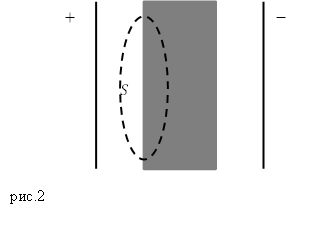
Задание: На рисунке 2 изображена замкнутая поверхность $S$ которая проходит так, что захватывает часть пластины изотропного диэлектрика. При этом известно, что поток вектора электрической индукции через эту поверхность равен нулю, а поток вектора напряженности больше нуля. Какие выводы можно сделать?

Если по условию задачи, поток вектора электрического смещения ($Ф_D$) через замкнутую поверхность равен нулю:

а он по теореме Остроградского — Гаусса $Ф_D$ равен суммарному свободному заряду, который находится внутри заданной поверхности, следовательно, то внутри этой поверхности нет свободных зарядов:

Но при этом сказано, что отличен от нуля поток вектора напряженности, но его поток равен сумме зарядов и свободных и связанных, следовательно, в диэлектрике присутствуют связанные заряды.

Ответ: Свободных зарядов нет, связанные заряды есть и их сумма положительна.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 04 12 2022

Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

Вектор электрической индукции

Вектором электрической индукции (электрического смещения) D → называют физическую величину, определяемую по системе С И :

D → = ε 0 E → + P → , где ε 0 — электрическая постоянная, E → — вектор напряженности, P → — вектор поляризации.

Вектор электрического смещения в СНС определяется как:

Видео:45. Электрическое смещениеСкачать

Вектор индукции

Значение вектора D → не является только полевым, потому как он учитывает поляризованность среды. Имеется связь с объемной плотностью заряда, выражаемая соотношением:

По уравнению d i v D → = ρ видно, что для D → единственным источником будут являться свободные заряды, на которых данный вектор начинается и заканчивается. В точках с отсутствующими свободными зарядами вектор электрической индукции является непрерывным. Изменения напряженности поля, вызванные наличием связанных зарядов, учитываются в самом векторе D → .

Видео:Урок 222. Поток вектора напряженности электрического поляСкачать

Связь вектора напряженности и вектора электрического смещения

При наличии изотропной среды запись связи вектора напряженности и вектора электрического смещения запишется как:

D → = ε 0 E → + ε 0 χ E → = ε 0 + ε 0 χ E → = ε ε 0 E → .

Где ε – диэлектическая проницаемость среды.

Наличие D → способствует облегчению анализа поля при наличии диэлектрика. Используя теорему Остроградского-Гаусса в интегральном виде с диэлектриком, фиксируется как:

Проходя через границу разделов двух диэлектриков для нормальной составляющей, вектор D → может быть записан:

D 2 n — D 1 n = σ

n 2 → D 2 → — D 1 → = σ ,

где σ – поверхностная плотность распределения зарядов на границе диэлектриков, n 2 → — нормаль, проведенная в сторону второй среды.

Формула тангенциальной составляющей:

D 2 τ = ε 2 ε 1 D 1 τ .

Единица вектора электрической индукции измеряется в системе С И как К л м 2 .

Поле вектора D → изображается при помощи линий электрического смещения.

Определение направления и густоты идет аналогично линиям вектора напряженности. Но линии вектора электрической индукции начинаются и заканчиваются только на свободных зарядах.

Имеются пластины плоского конденсатора с зарядом q . Произойдет ли изменение вектора электрической индукции при заполненном воздухом пространстве между пластинами и диэлектрика с диэлектрической проницаемостью ε ≠ ε υ o z d .

Поле конденсатора в первом случае характеризовалось вектором смещения ε v o z d = 1 , то есть D 1 → = ε v o z d ε 0 E 1 → = ε 0 E 1 → .

Необходимо заполнить пространство между пластинами конденсатора однородным и изотропным диэлектриком. При наличии поля в конденсаторе диэлектрик поляризуется. Тогда начинают появляться связанные заряды с плотностью σ s υ на его поверхности. Создается дополнительное поле с напряженностью:

Векторы полей E → ‘ и E 1 → имеют противоположные направления, причем:

Запись результирующего поля с диэлектриком примет вид:

E = E 1 — E ‘ = σ ε 0 — σ s υ ε 0 = 1 ε 0 σ — σ s υ .

Формула плотности связанных зарядов:

Произведем подстановку σ s υ = χ ε 0 E в E = E 1 — E ‘ = σ ε 0 — σ s υ ε 0 = 1 ε 0 σ — σ s υ , тогда:

Далее выражаем из ( 1 . 6 ) напряженность поля Е . Формула принимает вид:

E = E 1 1 + χ = E 1 ε .

Отсюда следует, что значение вектора электрической индукции в диэлектрике равняется:

D = ε ε 0 E 1 ε = ε 0 E 1 = D 1 .

Ответ: вектор электрической индукции не изменяется.

Была внесена пластина из диэлектрика с диэлектрической проницаемостью ε без свободных зарядов в зазор между разноименными заряженными пластинами. На рисунке 1 показана при помощи штриховой линии замкнутая поверхность. Определить поток электрической индукции Φ D через эту поверхность.

Рисунок 1 . Замкнутая поверхность

Формула записи потока вектора электрического смещения Φ D через замкнутую поверхность S :

Φ D = ∫ S D → · d S → .

Используя теорему Остроградского-Гаусса, можно сказать, что Φ D равняется суммарному свободному заряду, находящемуся внутри заданной поверхности. Из условия видно отсутствие свободных зарядов в диэлектрике и в имеющемся пространстве между пластинами конденсатора, а поток вектора индукции равняется нулю.

Изображена замкнутая поверхность S , проходящая с захватом части пластины изотропного диэлектрика на рисунке 2 . Поток вектора электрической индукции через нее равняется нулю, а поток вектора напряженности > 0 . Какой вывод можно сделать из данной задачи?

Рисунок 2 . Замкнутая поверхность с захватом части пластины изотропного диэлектрика

Из условия имеем, что поток вектора электрического смещения Φ D через замкнутую поверхность равняется нулю, то есть:

Если использовать теорему Остроградского-Гаусса, то значение Φ D – это суммарный свободный заряд, находящийся внутри заданной поверхности. Следует, что внутри такой поверхности отсутствуют свободные заряды:

Φ D = ∫ S D → · d S → = Q = 0 .

Имеем, что поток вектора напряженности не равен нулю, но он считается как сумма свободных и связанных зарядов. Отсюда вывод – диэлектрик содержит связанный заряды.

Ответ: свободные заряды отсутствуют, а связанные есть, причем с положительной их суммой.

Видео:Урок 218. Напряженность электрического поляСкачать

Вектор электрической индукции

Допустим, что одно вещество имеет диэлектрическую проницаемость равную $_1$, а вторая $_2$, тогда нормальная составляющая вектора напряженности электростатического поля ($E_n$) уменьшается во столько раз, во сколько увеличивается диэлектрическая проницаемость среды:

где $E_$ — нормальная компонента напряженности поля в веществе 1; $E_$ — нормальная составляющая электростатического поля во втором веществе. Отметим, что при переходе из одного вещества в другое тангенциальная компонента вектора напряженности ($E_$) изменяется без скачка. Говорят, что на границе двух веществ происходит «преломление» силовых линий поля.

Для сохранения всех преимуществ, которые дает теорема Остроградского — Гаусса при рассмотрении электростатического поля в вакууме, в веществе вводят физическую величину, которая не испытывает скачка при переходе из одного вещества в другое с разными $varepsilon $.

Так как при переходе из вакуума в вещество с диэлектрической проницаемостью равной $varepsilon $ число силовых линий уменьшается в $varepsilon $ раз, то векторная величина, равная:

будет оставаться неизменной при переходе из одного вещества в другое.

Видео:НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ суперпозиция полейСкачать

Определение вектора электрической индукции

Векторная величина, обозначаемая $overline$, равная:

где $overline

$ — вектор поляризации.

Выражение (3) является наиболее общим определение вектора электрической индукции (вектора электрического смещения). Для большинства диэлектриков (исключением являются, например, сегнетоэлектрики) вектор поляризации пропорционален напряженности поля:

В таком случае от формулы (3) мы приходим к определению вектора электрической индукции вида (2).

Название «вектор индукции» указывает на связь вектора $overline$ и явления электризации по влиянию (явление электростатической индукции).

Видео:ЧК_МИФ 3_1_5_3_(L3) ИСПОЛЬЗОВАНИЕ т.ГАУССА ДЛЯ ВЕКТОРА DСкачать

Физический смысл вектора электрической индукции

Допустим, что в веществе, с диэлектрической проницаемостью равной $varepsilon $ имеется очень тонкий вакуумный зазор, грани которого перпендикулярны направлению поля в точке рассмотрения (рис.1). В эту щель помещают точечный единичный положительный пробный заряд. Сила, с которой поле будет оказывать действие на этот пробный заряд, равна $overline.$

И так, вектор электрической индукции — это сила, которая действует на точечный единичный положительный заряд, находящийся в бесконечно узком зазоре, грани которого перпендикулярны направлению поля.

Силовые линии вектора $overline$ начинаются и заканчиваются на свободных зарядах. Величина $overline$ не зависит от диэлектрической проницаемости вещества.

В некоторых источниках вектор электрической индукции называют формальным, так как он равен сумме физических величин, относящихся к разным объектам к полю и к веществу (см формулу (3), где $overline$ — характеристика электрического поля; $overline

$ — характеристика вещества). Тогда говорят, что вектор электрической индукции не имеет физического смысла.

Видео:ЧК_МИФ:3_1_4_2 (L4- 4п. ) Использование векторов Р и D для описания поля в диэлектрикеСкачать

Теорема Гаусса — Остроградского для поля в диэлектрике

Поток вектора электрической индукции равен алгебраической сумме свободных зарядов, которые находятся внутри рассматриваемой замкнутой поверхности:

По теореме (5) поток вектора $overline$ через любую замкнутую поверхность равен нулю, если внутри данной поверхности нет свободных зарядов. Заряды, находящиеся вне рассматриваемой поверхности на поток вектора $overline$, не влияют.

Видео:Урок 225. Задачи на поток вектора напряженности электрического поляСкачать

Примеры задач с решением

Задание. Чему равен вектор поляризации в некоторой точке однородного изотропного диэлектрика, если известен вектор электрической индукции в этой точке ($overline$)? Диэлектрическая проницаемость вещества равна $varepsilon $.

Решение. За основу решения задачи примем определение вектора электрического смещения вида:

Выразим вектор поляризации из (1.1):

Так как по условию рассматриваемый диэлектрик является однородным и изотропным, то:

[overline=varepsilon _0overline left(1.3right),]

Подставим правую часть формулы (1.4) вместо $overline$ в уравнение (1.2), имеем:

Ответ. $overline

=left(1-fracright)overline$

Задание. Между двумя бесконечными заряженными пластинами, несущими одинаковые по величине, но противоположные по модулю заряды поместили пластину из диэлектрика. Пластина сторонних зарядов не имеет. Каков поток вектора электрической индукции через поверхность, которая изображена на рис.2?

Решение. В соответствии с теоремой Гаусса поток вектора электрической индукции равен алгебраической сумме свободных зарядов, которые находятся внутри выделенной замкнутой поверхности (рис.2). Так как по условию задачи свободных зарядов между пластинами и в диэлектрике нет, то поток вектора $overline$ будет равен нулю:

Ответ. $ointnolimits_S<overlinedoverline=0 >$

🌟 Видео

Лекция №4 "Диэлектрики, вектор электрической индукции"Скачать

Урок 223. Теорема ГауссаСкачать

46. Граничные условия для электрического поляСкачать

ЧК_МИФ 3_1_5_2_(L3) ВЕКТОР ЭЛЕКТРИЧЕСКОЙ ИНДУКЦИИСкачать

Основы электростатикиСкачать

43. Применение теоремы ГауссаСкачать

Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать

Лекция 237. Вектор электрической индукцииСкачать