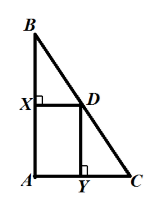Первая замечательная точка треугольника (4 видео)

Ззамечательные точки треугольника — свойства, применение и примеры решения

Замечательные точки треугольника не просто так описываются таким прилагательным. Для многих учеников, а начинают знакомиться с этим понятием в 8 классе, эта тема кажется наиболее интересной и простой в курсе геометрии, поэтому многочисленные теоремы и свойства запоминаются достаточно просто.

Итак, какие же четыре точки называются замечательными? Перечислим их:

точку пересечения медиан треугольника;

точку пересечения биссектрис треугольника;

точку пересечения высот треугольника;

точку пересечения серединных перпендикуляров сторон треугольника.

Все точки обладают своими особенностями и свойствами, про всех есть свои теоремы и следствия из них. Кроме того, существует свойство, которое справедливо сразу для четырёх этих точек. Вне зависимости от того, медиана ли это, биссектриса или высота, все они пересекаются в одной точке.

Замечательные точки характерны не только для треугольников. Например, в трапеции так же четыре замечательные точки.

Теперь рассмотрим основные положения, связанные с замечательными точками треугольника.

Содержание

Точка пересечения медиан треугольника
Точка пересечения биссектрис треугольника
Четыре замечательные точки треугольника
Точка пересечения медиан треугольника
Точка пересечения биссектрис треугольника
Готовые работы на аналогичную тему
Точка пересечения серединных перпендикуляров треугольника
Точка пересечения высот треугольника
Пример задачи на использование 4 замечательных точек треугольника
Исследовательский проект Замечательные точки треугольника
«Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
Выберите документ из архива для просмотра:
🔍 Видео

Видео:Первая замечательная точка треугольникаСкачать

Точка пересечения медиан треугольника

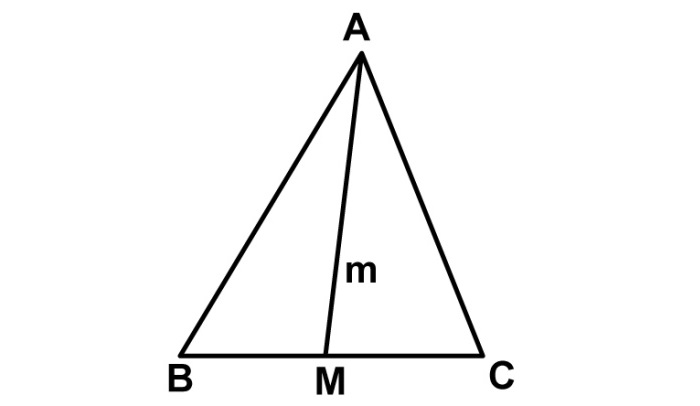
Из курса геометрии известно определение медианы треугольника.

На данном рисунке она обозначена прямой m, которая исходит из вершины А и заканчивается точкой М, являющейся центром стороны ВС.

Теперь сделаем чертёж треугольника, на котором укажем замечательную точку пересечения медиан.

Для начала постройте абсолютно любой треугольник и обозначьте его буквами А, В и С.

На отрезке АВ отметьте центр С₁, на стороне ВС центр А₁, на АС центр В_1.

Проведите 3 медианы из вершин. Из угла А – медиана АА₁,из угла В — медиана ВВ₁, из угла С — медиана СС_1.

Должно получиться так, как показано на рисунке: три проведённые линии пересекаются в одной точке G (что является их свойством).

Изучим следующее свойство точки пересечения трёх медиан треугольника.

Отрезки медианы треугольника, разделённой замечательной точкой, относятся друг к другу как 2:1. Проследим это свойство на примере используемого нами рисунка:

Видео:Первая замечательная точка треугольникаСкачать

Точка пересечения биссектрис треугольника

Прежде чем мы приступим к изучению следующей точки, рассмотрим теорему о биссектрисе, проведённой из вершины неразвёрнутого угла, и докажем её.

Видео:Первая замечательная точка треугольникаСкачать

Четыре замечательные точки треугольника

Вы будете перенаправлены на Автор24

В треугольнике есть так называемые четыре замечательные точки: точка пересечения медиан. Точка пересечения биссектрис, точка пересечения высот и точка пересечения серединных перпендикуляров. Рассмотрим каждую из них.

Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Точка пересечения медиан треугольника

О пересечении медиан треуголника: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.

Доказательство.

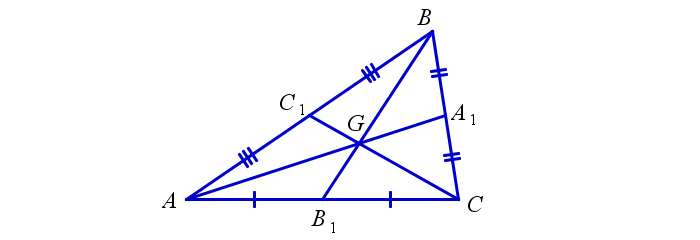
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 1).

Рисунок 1. Медианы треугольника

По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $angle ABB_1=angle BB_1A_1, angle BAA_1=angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда

Аналогично доказывается, что

Видео:ГЕОМЕТРИЯ 8 класс: 4 замечательные точкиСкачать

Точка пересечения биссектрис треугольника

О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

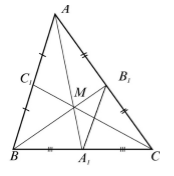
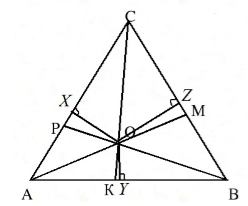
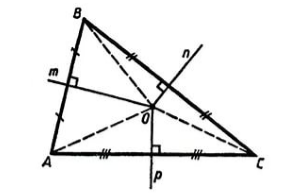
Рассмотрим треугольник $ABC$, где $AM, BP, CK$ его биссектрисы. Пусть точка $O$ — точка пересечения биссектрис $AM и BP$. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).

Рисунок 2. Биссектрисы треугольника

Готовые работы на аналогичную тему

Для доказательства нам потребуется следующая теорема.

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

По теореме 3, имеем: $OX=OZ, OX=OY$. Следовательно, $OY=OZ$. Значит точка $O$ равноудалена от сторон угла $ACB$ и, значит, лежит на его биссектрисе $CK$.

Видео:Замечательные точки треугольника. Медиана треугольника.Скачать

Точка пересечения серединных перпендикуляров треугольника

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство.

Пусть дан треугольник $ABC$, $n, m, p$ его серединные перпендикуляры. Пусть точка $O$ — точка пересечения серединных перпендикуляров $n и m$ (рис. 3).

Рисунок 3. Серединные перпендикуляры треугольника

Для доказательства нам потребуется следующая теорема.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.

По теореме 3, имеем: $OB=OC, OB=OA$. Следовательно, $OA=OC$. Значит точка $O$ равноудалена от концов отрезка $AC$ и, значит, лежит на его серединном перпендикуляре $p$.

Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Точка пересечения высот треугольника

Высоты треугольника или их продолжения пересекаются в одной точке.

Доказательство.

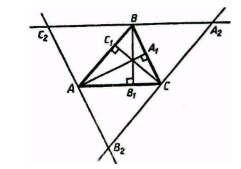
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник $A_2B_2C_2$ (рис. 4).

Рисунок 4. Высоты треугольника

Так как $AC_2BC$ и $B_2ABC$ параллелограммы с общей стороной, то $AC_2=AB_2$, то есть точка $A$ — середина стороны $C_2B_2$. Аналогично, получаем, что точка $B$ — середина стороны $C_2A_2$, а точка $C$ — середина стороны $A_2B_2$. Из построения мы имеем, что $_1bot A_2B_2, _1bot A_2C_2, _1bot C_2B_2$. Следовательно, $_1, _1, _1$ — серединные перпендикуляры треугольника $A_2B_2C_2$. Тогда, по теореме 4, имеем, что высоты $_1, _1, _1$ пересекаются в одной точке.

Видео:четыре замечательные точки треугольника 8 КЛАСС АтанасянСкачать

Пример задачи на использование 4 замечательных точек треугольника

Серединные перпендикуляры к сторонам $AB$ и $AC$ треугольника $ABC$ пересекаются в точке $D$ стороны $BC$. Докажите, что

а) точка $D$ — середина стороны $BC$.

б) $angle A=angle B+angle C$

Решение.

а) По теореме 4, все серединные перпендикуляры пересекаются в точке $D$. Следовательно, $D$ — основание серединного перпендикуляра к стороне $BC$. Значит точка $D$ — середина стороны $BC$.

б) Так как $X$ и $D$ — середины сторон, то $XD$ — средняя линия треугольника. Тогда, по теореме о средней линии треугольника $XD||AC$. Значит,$angle A=angle DXB$, как соответственные углы. Значит, $angle A=^0$. Тогда$angle B+angle C=^0-angle A=^0-^0=^0=angle A$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 29 03 2022

Видео:Четыре замечательные точки треугольника. Видеоурок 20. Геометрия 8 классСкачать

Исследовательский проект Замечательные точки треугольника

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Kurchavov_Alexandr-1.doc

Глава1. Исторические сведения о замечательных точках треугольника

1.2. Медианы треугольника

1.3. Биссектрисы треугольника

1.4. Высоты в треугольнике

1.5. Серединные перпендикуляры к сторонам треугольника

Глава 2. Исследование замечательных точек треугольника.

Список использованной литературы

Геометрия — это раздел математики, который рассматривает различные фигуры и их свойства. Геометрия начинается с треугольника. Вот уже два с половиной тысячелетия треугольник является символом геометрии; но он не только символ, треугольник — атом геометрии.

В своей работе я рассмотрю свойства точек пересечения биссектрис, медиан и высот треугольника, расскажу о замечательных их свойствах и линиях треугольника.

К числу таких точек, изучаемых в школьном курсе геометрии, относятся:

а) точка пересечения биссектрис (центр вписанной окружности);

б) точка пересечения серединных перпендикуляров (центр описанной окружности);

в) точка пересечения высот (ортоцентр);

г) точка пересечения медиан (центроид).

Актуальность: расширить свои знания о треугольнике, свойствах его замечательных точек.

Цель: исследование треугольника на его замечательные точки, изучение их классификаций и свойств.

1. Изучить необходимую литературу

2. Изучить классификацию замечательных точек треугольника

3. Уметь строить замечательные точки треугольника.

4. Обобщить изученный материал для оформления буклета.

умение находить замечательные точки в любом треугольнике, позволяет решать геометрические задачи на построение.

Глава 1. Исторические сведения о замечательных точках треугольника

В четвертой книге «Начал» Евклид решает задачу: «Вписать круг в данный треугольник». Из решения вытекает, что три биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанного круга. Из решения другой задачи Евклида вытекает, что перпендикуляры, восстановленные к сторонам треугольника в их серединах, тоже пересекаются в одной точке – центре описанного круга. В «Началах» не говорится о том, что и три высоты треугольника пересекаются в одной точке, называемой ортоцентром (греческое слово «ортос» означает «прямой», «правильный»). Это предложение было, однако, известно Архимеду, Паппу, Проклу.

Четвертой особенной точкой треугольника является точка пересечения медиан. Архимед доказал, что она является центром тяжести (барицентром) треугольника. На вышеназванные четыре точки было обращено особое внимание, и начиная с XVIII века они были названы «замечательными» или «особенными» точками треугольника.

Исследование свойств треугольника, связанных с этими и другими точками, послужило началом для создания новой ветви элементарной математики – «геометрии треугольника» или «новой геометрии треугольника», одним из родоначальников которой стал Леонард Эйлер. В 1765 году Эйлер доказал, что в любом треугольнике ортоцентр, барицентр и центр описанной окружности лежат на одной прямой, названной позже «прямой Эйлера».

Треугольник — геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки — вершины треугольника, отрезки — стороны треугольника.

В А, В, С — вершины

АВ, ВС, СА — стороны

С каждым треугольником связаны четыре точки:

Точка пересечения медиан;

Точка пересечения биссектрис;

Точка пересечения высот.

Точка пересечения серединных перпендикуляров;

1.2. Медианы треугольника

Медина треугольника ― отрезок , соединяющий вершину треугольника с серединой противоположной стороны (Рисунок 1). Точка пересечения медианы со стороной треугольника называется основанием медианы.

Рисунок 1. Медианы треугольника

Построим середины сторон треугольника и проведем отрезки, соединяющую каждую из вершин с серединой противолежащей стороны. Такие отрезки называются медианой.

И вновь мы наблюдаем, что и эти отрезки пересекаются в одной точке. Если мы измерим длины получившихся отрезков медиан, то можно проверить еще одно свойство: точка пересечения медиан делит все медианы в отношении 2:1, считая от вершин. И еще, треугольник, который опирается на острие иглы в точке пересечения медиан, находится в равновесии! Точка, обладающая таким свойством, называется центром тяжести (барицентр). Центр равных масс иногда называют центроидом. Поэтому свойства медиан треугольника можно сформулировать так: медианы треугольника пересекаются в центре тяжести и точкой пересечения делятся в отношении 2:1, считая от вершины.

1.3. Биссектрисы треугольника

Биссектрисой треугольника называется отрезок биссектрисы угла, проведенный от вершины угла до её пересечения с противолежащей стороной. У треугольника существуют три биссектрисы, соответствующие трём его вершинам (Рисунок 2).

Рисунок 2. Биссектриса треугольника

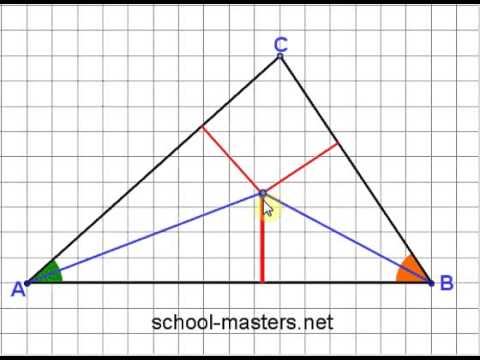
В произвольном треугольнике ABC проведем биссектрисы его углов. И вновь при точном построении все три биссектрисы пересекутся в одной точке D. Точка D – тоже необычная: она равноудалена от всех трех сторон треугольника. В этом можно убедиться, если опустить перпендикуляры DA 1, DB 1 и DC1 на стороны треугольника. Все они равны между собой: DA1=DB1=DC1.

Если провести окружность с центром в точке D и радиусом DA 1, то она будет касаться всех трех сторон треугольника (то есть будет иметь с каждым из них только одну общую точку). Такая окружность называется вписанной в треугольник. Итак, биссектрисы углов треугольника пересекаются в центре вписанной окружности.

1.4. Высоты в треугольнике

Высота треугольника — перпендикуляр , опущенный из вершины треугольника на противоположную сторону или прямую, совпадающую с противоположной стороной. В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника (Рисунок 3).

Рисунок 3. Высоты в треугольниках

Если в треугольнике построить три высоты, то все они пересекутся в одной точке H. Эта точка называется ортоцентром. (Рисунок 4).

С помощью построений можно проверить, что в зависимости от вида треугольника ортоцентр располагается по – разному:

у остроугольного треугольника – внутри;

у прямоугольного – на гипотенузе;

у тупоугольного – снаружи.

Рисунок 4. Ортоцентр треугольника

Таким образом, мы познакомились еще с одной замечательной точкой треугольника и можем сказать, что: высоты треугольника пересекаются в ортоцентре.

1.5. Серединные перпендикуляры к сторонам треугольника

Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.

Начертим произвольный треугольник ABC и проведем серединные перпендикуляры к его сторонам. Если построение выполнено точно, то все перпендикуляры пересекутся в одной точке – точке О. Эта точка равноудалена от всех вершин треугольника. Другими словами, если провести окружность с центром в точке О, проходящую через одну из вершин треугольника, то она пройдет и через две другие его вершины.

Окружность, проходящая через все вершины треугольника, называется описанной около него. Поэтому установленное свойство треугольника можно сформулировать так: серединные перпендикуляры к сторонам треугольника пересекаются в центре описанной окружности (Рисунок 5).

Рисунок 5. Треугольник вписанный в окружность