Если в четырехугольник можно вписать окружность то биссектрисы его углов пересекаются в одной точке (4 видео)

Please wait.

Содержание

We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
What can I do to prevent this in the future?
Если в четырехугольник можно вписать окружность то биссектрисы его углов пересекаются в одной точке
Вписанная окружность
Доказательство
Доказательство
Доказательство
Доказательство
Доказательство
Доказательство
📹 Видео

Видео:Биссектрисы пересекаются в одной точке| Задачи 11-20 | Решение задач | Волчкевич|Уроки геометрии 7-8Скачать

We are checking your browser. mathvox.ru

Видео:Биссектрисы пересекаются в одной точке| Задачи 28-33 | Решение задач | Волчкевич|Уроки геометрии 7-8Скачать

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

Видео:Биссектрисы пересекаются в одной точке| Задачи 1-10 | Решение задач | Волчкевич| Уроки геометрии 7-8Скачать

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Cloudflare Ray ID: 6c9eabea6c6d3a6b • Your IP : 85.95.179.65 • Performance & security by Cloudflare

Видео:Геометрия Если четырехугольник является описанным около окружности, то суммы его противолежащихСкачать

Если в четырехугольник можно вписать окружность то биссектрисы его углов пересекаются в одной точке

Ключевые слова: окружность, описанная окружность, центр окружности, вписанная окружность, треугольник, четырехугольник, вневписанная окружность

Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон.

Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.

Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.
Сам многоугольник в таком случае называется описанным около данной окружности.
Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.

Для произвольного многоугольника невозможно вписать в него и описать около него окружность.
Для треуголь ника это всегда возможно.

Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а её центр находится внутри окружности

Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.
Радиус вписанной в треугольник окружности равен отношению площади треугольника и его полупериметра: $$r = frac~~$$ , где S — площадь треугольника, а $$p =frac$$ — полупериметр треугольника.~~

Серединным перпендикуляром называют прямую перпендикулярную отрезку и проходящую через его середину.

~~Окружность называется описанной около треугольника, если она проходит через три его вершины.~~

~~Вокруг любого треугольника можно описать окружность, и только одну.~~
В любом треугольнике сторона равна произведению диаметра описанной окружности и синуса противолежащего угла.
Площадь треугольника равна отношению произведения длин всех его сторон к учетверенному радиусу окружности, описанной около этого треугольника: $$R =frac $$, где S — площадь треугольника.

Центр вневписанной окружности лежит на пересечении биссектрис внешних углов, при вершинах касаемой стороны, и биссектрисы угла при третей вершине.

~~Окружность, вписанная в прямоугольный треугольник~~

Радиус вписанной окружности находят по формулам: $$r = frac $$, и $$r = frac $$, где a и b катеты прямоугольного треугольника, а c гипотенуза прямоугольного треугольника.

~~Окружность, описанная около прямоугольного треугольника~~

~~Центр описанной окружности совпадает с серединой гипотенузы.~~
~~Радиус равен половине гипотенузы: $$R = frac$$.~~
~~Радиус равен медиане, проведенной к гипотенузе: $$R = m_$$.~~

~~Четырехугольник, вписанный в окружность~~

Четырехугольник можно вписать в окружность, если сумма противолежащих углов равна $$180^circ: alpha + beta + gamma +delta = 180^circ$$.
~~Если четырехугольник вписан в окружность, то суммы противолежащих углов равны $$180^circ$$.~~
Сумма произведений противолежащих сторон четырехугольника ABCD равна произведению диагоналей: $$ABcdot DC + AD cdot BC = BD cdot AC$$.
~~Площадь: $$S = sqrt$$, где $$p = frac $$ — полупериметр четырехугольника.~~

~~Окружность, вписанная в ромб~~

~~В любой ромб можно вписать окружность.~~
Радиус r вписанной окружности: $$r = frac$$, где h — высота ромба или $$r = frac <d_cdot d_>$$, где a — сторона ромба, d₁ и d₂ — диагонали ромба.

~~Видео:Если в четырёхугольник можно вписать окружность Скачать~~

Вписанная окружность

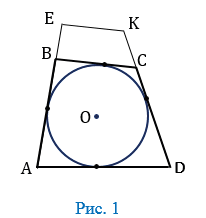
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность. На рисунке 1 четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.

~~Теорема~~

В любой треугольник можно вписать окружность.

Доказательство

Дано: произвольный АВС.

Доказать: в АВС можно вписать окружность.

~~Доказательство:~~

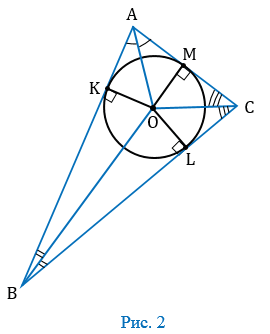
1. Проведем биссектрисы углов А, В и С, которые пересекутся в точке О (следствие из свойства биссектрис). Из точки О проведем перпендикуляры ОК, ОL и ОМ соответственно к сторонам АВ, ВС и СА (Рис. 2).

2. Точка О равноудалена от сторон АВС (свойство биссектрис), поэтому ОК = ОL = ОМ. Следовательно, окружность с центром О радиуса ОК проходит через точки К, L и М. Стороны АВС касаются этой окружности в точках К, L, М, т.к. они перпендикулярны к радиусам ОК, ОL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в АВС. Теорема доказана.

~~Замечание 1~~

В треугольник можно вписать только одну окружность.

Доказательство

Предположим, что в треугольник можно вписать две окружности. Тогда центр каждой окружности равноудален от сторон треугольника и, значит, совпадает с точкой О пересечения биссектрис треугольника, а радиус равен расстоянию от точки О до сторон треугольника. Следовательно, эти окружности совпадают, значит в треугольник можно вписать только одну окружность. Что и требовалось доказать.

~~Замечание 2~~

Площадь треугольника равна произведению его полупериметра на радиус вписанной в него окружности.

Доказательство

На рисунке 2 мы видим, что АВС составлен из трех треугольников: АВО, ВСО и САО. Пусть АВ, ВС и АС основания треугольников АВО, ВСО и САО соответственно, тогда высотами данных треугольников окажутся отрезки ОК = ОL = ОМ = r ( r — радиус окружности с центром О). Следовательно, площади этих треугольников вычисляются по формулам: . Тогда, по свойству площадей, площадь треугольника АВС выражается формулой: , где — периметр АВС. Что и требовалось доказать.

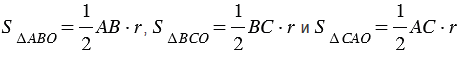
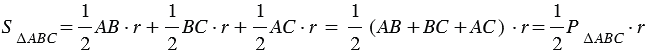
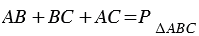
~~Замечание 3~~

Не во всякий четырехугольник можно вписать окружность.

Доказательство

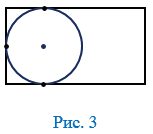
Рассмотрим, например, прямоугольник, у которого смежные стороны не равны, т.е. прямоугольник, не являющийся квадратом. В такой прямоугольник можно «поместить» окружность, касающуюся трех его сторон (Рис.3), но нельзя «поместить» окружность так, чтобы она касалась всех четырех его сторон, т.к. диаметр окружности меньше большей стороны прямоугольника т.е. нельзя вписать окружность. Что и требовалось доказать.

Если же в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:

В любом описанном четырехугольнике суммы противоположных сторон равны.

Доказательство

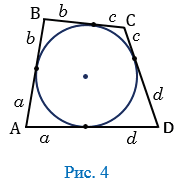
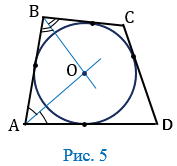
~~Рассмотрим четырехугольник АВСD, описанный около окружности (Рис. 4).~~

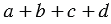
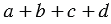
На рисунке 4 одинаковыми буквами обозначены равные отрезки касательных, т.к. отрезки касательных к окружности, проведенные из одной точки, равны. Тогда АВ + СD = и ВС + АD = , следовательно, АВ + СD = ВС + АD.

~~Верно и обратное утверждение:~~

Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

Доказательство

Пусть в выпуклом четырехугольнике АВСD

АВ + СD = ВС + АD. (1)

Точка О пересечения биссектрис углов А и В равноудалена от сторон АD, АВ и ВС (свойство биссектрис), поэтому можно провести окружность с центром О, касающуюся указанных трех сторон (Рис. 5).

~~Докажем, что эта окружность касается также стороны СD и, значит, является вписанной в четырехугольник АВСD.~~

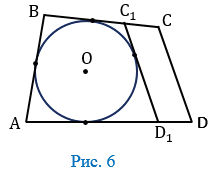
Предположим, что это не так. Тогда прямая СD либо не имеет общих точек с окружностью, либо является секущей. Рассмотрим первый случай (Рис. 6). Проведем касательную С₁D₁, параллельную стороне СD (С₁ и D₁ — точки пересечения касательной со сторонами ВС и АD).

~~Так как АВС₁D₁ — описанный четырехугольник, то по свойству его противоположных сторон~~

АВ + С₁D₁ = ВС₁ + AD₁. (2)

~~Но ВС₁ = ВС — С₁С, АD₁ = АD — D₁D, поэтому из равенства (2) получаем:~~

С₁D₁ + С₁С + D₁D = ВС + АD — АВ.

~~Правая часть этого равенства в силу (1) равна СD. Следовательно, приходим к равенству~~

т.е. в четырехугольник С₁СDD₁ одна сторона равна сумме трех других сторон. Но этого не может быть, т.к. к аждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон. Значит, наше предположение ошибочно. Аналогично можно доказать, что прямая CD не может быть секущей окружности. Следовательно, окружность касается стороны СD. Что и требовалось доказать.