Какое из следующих утверждений верно?
1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
В ответ запишите номер выбранного утверждения.
Рассмотрим каждое из утверждений:
1) «Все углы ромба равны» — неверно. Верно только в случае квадрата.
2) «Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны» — неверно. Стороны квадрата и ромба могут быть равны, однако такие четырёхугольники не равны.
3) «Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности» — верно.
Видео:№366. Найдите стороны четырёхугольника, если его периметр равен 8 смСкачать

Если стороны четырехугольника равны сторонам другого четырехугольника то они равны соответственно
Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Источник задания: Решение 4955. ОГЭ 2018 Математика, И.В. Ященко. 36 вариантов.
Задание 20. Какое из следующих утверждений верно?
1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
1) Не верно. У ромба противоположные углы равны, но не все.
2) Не верно. Четырехугольники могут иметь равные стороны, но разные углы.
3) Верно. Эта точка будет точкой пересечения касательных.
Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

Признаки равенства четырехугольников
При изучении признаков равенства треугольников в курсе геометрии 7 класса возникли вопросы: Существуют ли признаки равенства четырёхугольников? Если да, то по скольким элементам? Можно ли их сформулировать и доказать, опираясь на признаки равенства треугольников?
Цель: Сформулировать и доказать признаки равенства четырёхугольников.
Задачи: 1) Изучить литературу по данной теме.
2) Исследовать все различные комбинации наборов сторон и углов из четырёх элементов и, либо доказать признак, либо опро- вергнуть его, приведя контрпример.
3) Исследовать все случаи различных комбинаций из 5 элементов, сформулировать и доказать признак, либо опровергнуть.
Две геометрические фигуры называются равными, если их можно совместить наложением.
Два четырехугольника называются равными, если их можно совместить наложением.
Существуют признаки равенства четырехугольников по четырем элементам.
ПО ЧЕТЫРЁМ УГЛАМ
2)ПО ТРЁМ УГЛАМ И СТОРОНЕ а)
3)ПО ДВУМ УГЛАМ И ДВУМ СТОРОНАМ а)
4) ПО УГЛУ И ТРЁМ СТОРОНАМ а) BC=BC1
5)ПО ЧЕТЫРЁМ СТОРОНАМ
BC=BC1, CD=CD1, AD=AD1
(смотри Приложение №1 — с. 29 )
ПРИЗНАКОВ РАВЕНСТВА ЧЕТЫРЁХУГОЛЬНИКОВ ПО ЧЕТЫРЁМ
ЭЛЕМЕНТАМ НЕ СУЩЕСТВУЕТ.
Существуют признаки равенства четырёхугольников по пяти элементам.
Если четыре стороны и угол одного четырёхугольника соответственно равны четырём сторонам и углу другого четырёхугольника, то такие четырёхугольники равны.
ABCD И A[]B[]C[]D[]- четырёхугольники. AB=A[]B[], BC= B[]C[], CD=C[]D[],
Вывод: Т. к. соответственные стороны и соответственные углы четырёхугольников равны, то они совместятся наложением, а значит- по определению равных фигур — ABCD=A[]B[]C[]D[].
Если три стороны и два угла между ними одного четырёхугольника соответственно равны трём сторонам и двум углам между ними другого четырёхугольника, то такие четырёхугольники равны.
Т. к. соответственные стороны и углы четырёхугольников равны, то они совместятся наложением, а значит- по определению равных
Если три стороны и два угла, не лежащие между ними, одного четырёхугольника соответственно равны трём сторонам и двум углам, не лежащим между ними, другого четырёхугольника, то такие четырёхугольники равны.
Случай, где углы четырёхугольника тупые доказывается аналогично, достаточно перейти к смежным, соответственно равным углам.
Если два противолежащих угла и три стороны одного четырёхугольника соответственно равны двум противолежащим углам и трём сторонам другого четырёхугольника, то такие четырёхугольники равны.
Если три угла и две стороны между ними одного четырёхугольника соответственно равны трём углам и двум сторонам между ними другого четырёхугольника, то такие четырёхугольники равны.
Если три угла и две смежные стороны, не лежащие между ними, одного четырёхугольника, соответственно равны трём углам и двум сторонам, не лежащим между ними , другого четырёхугольника, то такие четырёхугольники равны.
Если три угла и две смежные стороны, одна из которых лежит между данными углами, одного четырёхугольника, соответственно равны трём углам и двум смежным сторонам, одна из которых лежит между двумя данными углами другого четырёхугольника, то такие четырёхугольники равны.
По стороне и четырём углам
1) Эмпирические (изучение литературы, сбор сведений, сбор и обработка статистического материала)
2) Теоретические (сравнение и обобщение данных, составление таблиц)
3) Практические (построения с помощью циркуля и линейки, доказательства).
1) Изучение и исследование материала по теме.
2) Изучение проблемы.
3) Обработка материала и выработка практических рекомендаций.
1) Рассмотрев все различные наборы из четырёх элементов (сторон и углов) четырёхугольника, получили 12 случаев, к каждому из них с помощью циркуля и линейки привели контрпример, построив 2 неравных четырёхугольника по данным элементам.
2) Рассмотрев все различные наборы из 5 элементов четырёхугольника, получили 10 случаев, 7 из которых стали признаками равенства четырёхугольников, а к 3 случаям привели контрпример, построив неравные между собой четырёхугольники.
При изучении данной темы было установлено: существуют признаки равенства четырёхугольников по 5 элементам.
1. По 4 сторонам и углу: если четыре стороны и угол одного четырёхугольника соответственно равны четырем сторонам и углу другого четырёхугольника, то такие четырёхугольники равны.
2. По 3 сторонам и 2 углам между ними: если три стороны и два угла между ними одного четырёхугольника соответственно равны трем сторонам и двум углам между ними другого четырёхугольника, то такие четырёхугольники равны.
3. По 3 сторонам и 2 углам, не лежащим между ними: если три стороны и два угла, не лежащие между ними, одного четырёхугольника соответственно равны трем сторонам и двум углам, не лежащим между ними, другого четырёхугольника, то такие четырёхугольники равны.
4. По 2 противолежащим углам и 3 сторонам: если два противолежащих угла и три стороны одного четырёхугольника соответственно равны двум противолежащим углам и трем сторонам другого четырёхугольника, то такие четырёхугольники равны.
5. По 3 углам и 2 сторонам между ними: если три угла и две стороны между ними одного четырёхугольника соответственно равны трем углам и двум сторонам между ними другого четырёхугольника, то такие четырёхугольники равны.
6. По 3 углам и 2 смежным сторонам, не лежащим между ними: если три угла и две смежные стороны, не лежащие между ними, одного четырёхугольника соответственно равны трем углам и двум смежным сторонам, не лежащим между ними, другого четырёхугольника, то такие четырёхугольники равны.
7. По 3 углам и 2 смежным сторонам, одна из которых лежит между данными углами: если три угла и две смежные стороны, одна из которых лежит между данными углами, одного четырёхугольника соответственно равны трем углам и двум смежным сторонам, одна из которых лежит между данными углами другого четырёхугольника, то такие четырёхугольники равны.
Была проделана работа по доказательству признаков равенства четырёхугольников. Для доказательства были использованы признаки равенства треугольников, определение равных фигур, геометрические построения с помощью циркуля и линейки.
В результате работы сформулировали и доказали 7 признаков по пяти элементам. Эти признаки могут быть полезны для тех, кто начинает изучать геометрию, учится сам формулировать и доказывать теоремы, а также в практической деятельности человека, например, при нахождении площадей.
📽️ Видео
Если две стороны и угол одного треугольника равны ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Геометрия. 7 класс. Теоремы. Т8. Третий признак равенства треугольников.Скачать
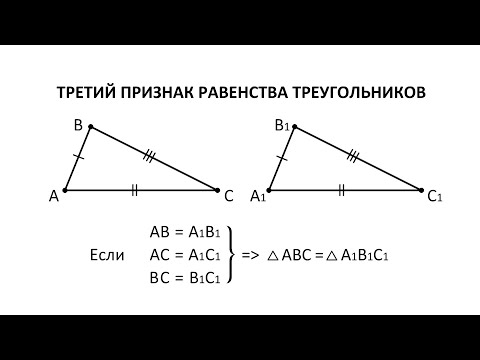
Геометрия. 7 класс. Теоремы. Т3. Первый признак равенства треугольников.Скачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Геометрия. 7 класс. Теоремы. Т7. Второй признак равенства треугольников.Скачать
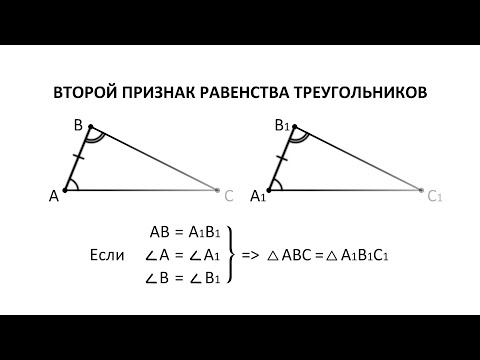
7 класс, 15 урок, Первый признак равенства треугольниковСкачать

№368. Найдите углы выпуклого четырехугольника, если они равны друг другу.Скачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Если стороны одного четырёхугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Диагонали четырехугольника равны 4 и 5.Скачать

Второй признак равенства треугольников. 7 класс.Скачать

Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

№92. Периметр одного треугольника больше периметра другого. Могут ли быть равными этиСкачать

Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Первый признак равенства треугольников. 7 класс.Скачать

Признаки равенства треугольников. 7 класс.Скачать

№135. Докажите, что если сторона одного равностороннего треугольника равна стороне другогоСкачать

