Если прямая перпендикулярна к двум параллельным прямым лежащим в плоскости то (5 видео)

Перпендикулярность прямых и плоскостей

Содержание

Перпендикулярные прямые
Перпендикулярность прямой и плоскости
Признак перпендикулярности прямой и плоскости
Свойства перпендикулярных прямой и плоскости
Перпендикулярность плоскостей
Признак перпендикулярности плоскостей
Свойство перпендикулярных плоскостей
Геометрия. 10 класс
Прямая, перпендикулярная к плоскости. Признак перпендикулярности прямой и плоскости. Расстояние от точки до плоскости
Прямая, перпендикулярная к плоскости. Признак перпендикулярности прямой и плоскости
Свойства перпендикуляра к плоскости
💥 Видео

Видео:10 класс, 17 урок, Признак перпендикулярности прямой и плоскостиСкачать

Перпендикулярные прямые

Две прямые в пространстве называются перпендикулярными , если угол между ними составляет .

При этом прямые могут пересекаться,

а могут быть скрещивающимися:

Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Перпендикулярность прямой и плоскости

Прямая называется перпендикулярной к плоскости , если она перпендикулярна любой прямой, лежащей в этой плоскости.

Признак перпендикулярности прямой и плоскости

Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Свойства перпендикулярных прямой и плоскости

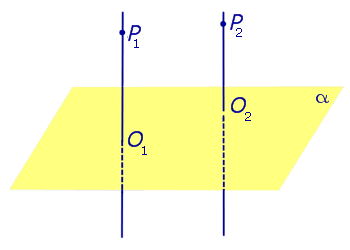
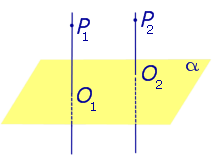
1). Две прямые, перпендикулярные одной и той же плоскости, параллельны.

2). Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости.

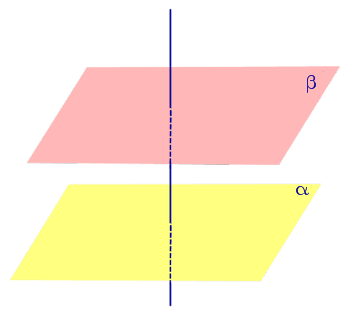
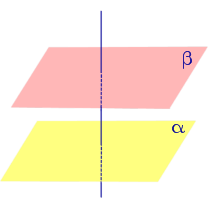
3). Две плоскости, перпендикулярные одной и той же прямой, параллельны между собой

Видео:10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

Перпендикулярность плоскостей

Пересекающиеся плоскости называются перпендикулярными , если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Признак перпендикулярности плоскостей

Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Свойство перпендикулярных плоскостей

Если прямая лежит в одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна второй плоскости.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Геометрия 10 класс (Урок№9 - Признак перпендикулярности прямой и плоскости.)Скачать

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок № 8 Перпендикулярность прямой и плоскости

Перечень вопросов, рассматриваемых по теме

Ввести понятие перпендикулярных прямых в пространстве;
Доказать лемму о перпендикулярности двух параллельных прямых;
Решать задачи по теме.

Глоссарий по теме

Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90. Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.

Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости

Теорема о прямой перпендикулярной к плоскости. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл. Базовый и профильный уровень. М.: Просвещение, 2015. С.1-10.

Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 9 класса. Базовый и профильный уровень

Зив Б.Г. Геометрия. Дидактические материалы. 10-11 класс М.: Просвещение, 2015.

Открытые электронные ресурсы:

Перпендикулярность прямой и плоскости. http://school-collection.edu.ru // Единая коллекция цифровых образовательных ресурсов.

Перпендикулярность прямой и плоскости. https://www.yaklass.ru // Я-класс. Образовательный портал Сколково.

Теоретический материал для самостоятельного изучения

Через точку М пространства, не лежащую на данных прямых, проведем прямые МА и МС, параллельные соответственно прямым а и с. Так как а ⊥ с, то ∠АМС=90 о .

Итак, прямые b и с параллельны соответственно прямым МА и МС, угол между ними равен 90 о , т.е. b ‖ МА, с ‖ МС, угол между МА и МС равен 90 о

Это означает, что угол между прямыми b и с также равен 90 о , то есть b ⊥ с.

Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

Проведем какую-нибудь прямую x в плоскости α, т.е. x ∊ α.Так как а ⊥ α, то а ⊥ x.

По лемме о перпендикулярности двух параллельных прямых к третьей а₁ ⊥ x.

Таким образом, прямая а₁ перпендикулярна к любой прямой, лежащей в плоскости α, т. е. а₁ ⊥ α

Теорема. Ели две прямые перпендикулярны плоскости, то они параллельны.

Через какую-нибудь точку М прямой b проведем прямую b₁, параллельную прямой а.

Докажем, что прямая b₁ совпадает с прямой b. Тем самым будем доказано, что а ‖ b. Допустим, что прямые b₁ и b не совпадают. Тогда в плоскости β, содержащей прямые b и b₁, через точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости α и β. Но это невозможно, следовательно, а ‖ b, т.е. b ∊ β, b₁ ∊ β, α β = c (невозможно)→ а ‖ b

Теорема. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Пусть дана плоскость α и точка М (см. рис. 2). Нужно доказать, что через точку М проходит единственная прямая с, перпендикулярная плоскости α.

Проведем прямую а в плоскости α (см. рис. 3). Согласно доказанному выше утверждению, через точку М можно провести плоскость γ перпендикулярную прямой а. Пусть прямая b – линия пересечения плоскостей α и γ.

В плоскости γ через точку М проведем прямую с, перпендикулярную прямой b.

Прямая с перпендикулярна b по построению, прямая с перпендикулярна а (так как прямая а перпендикулярна плоскости γ, а значит, и прямой с, лежащей в плоскости γ). Получаем, что прямая с перпендикулярна двум пересекающимся прямым из плоскости α. Значит, по признаку перпендикулярности прямой и плоскости, прямая с перпендикулярна плоскости α. Докажем, что такая прямая с единственная.

Предположим, что существует прямая с₁, проходящая через точку М и перпендикулярная плоскости α. Получаем, что прямые с и с₁ перпендикулярны плоскости α. Значит, прямые с и с₁ параллельны. Но по построению прямые с и с₁пересекаются в точке М. Получили противоречие. Значит, существует единственная прямая, проходящая через точку М и перпендикулярная плоскости α, что и требовалось доказать.

Теоретический материал для углубленного изучения

Доказательство (см. рис. 1)

Пусть нам дана прямая а и точка М. Докажем, что существует плоскость γ, которая проходит через точку М и которая перпендикулярна прямой а.

Через прямую а проведем плоскости α и β так, что точка М принадлежит плоскости α. Плоскости α и β пересекаются по прямой а. В плоскости α через точку М проведем перпендикуляр MN (или р) к прямой а, . В плоскости β из точки N восстановим перпендикуляр q к прямой а. Прямые р и q пересекаются, пусть через них проходит плоскость γ. Получаем, что прямая а перпендикулярна двум пересекающимся прямым р и q из плоскости γ. Значит, по признаку перпендикулярности прямой и плоскости, прямая а перпендикулярна плоскости γ.

Примеры и разборы решения заданий тренировочного модуля

Выбор элемента из выпадающего списка

Выпишите ребра, перпендикулярные плоскости (DC).

Правильный вариант/варианты (или правильные комбинации вариантов):

Неправильный вариант/варианты (или комбинации):

Подсказка: в кубе все углы по . Плоскость (DC), проходит через грань куба DC.

Разбор задания: Куб – это геометрическая фигура у которой все углы прямые, следовательно нужно увидеть ребра которые перпендикулярны к плоскости (DC), к грани куба (DDC).Эти ребра — AD, A₁D₁, BC, B₁C₁

Закончите предложение, чтобы получилось верное утверждение.

Две прямые называются перпендикулярными, если …..
Если плоскости перпендикулярна одной из двух параллельных прямых, то она ……

параллельны
один
она перпендикулярна к любой прямой, лежай в этой плоскости.
перпендикулярна плоскости.

Правильный вариант/варианты (или правильные комбинации вариантов):

Две прямые называются перпендикулярными, если …

угол между ними равен 90

Если плоскость перпендикулярна одной из двух параллельных прямых, то она …

перпендикулярна и другой

Неправильный вариант/варианты (или комбинации):

Лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к третьей прямой.

Теорема: если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

Видео:12.1 Признак перпендикулярности прямой и плоскостиСкачать

Прямая, перпендикулярная к плоскости.
Признак перпендикулярности прямой и плоскости.
Расстояние от точки до плоскости

Если прямая перпендикулярна к двум параллельным прямым лежащим в плоскости то

Прямая, перпендикулярная к плоскости. Признак перпендикулярности прямой и плоскости

Свойства перпендикуляра к плоскости. Расстояние от точки до плоскости

Видео:17. Признак перпендикулярности прямой и плоскостиСкачать

Прямая, перпендикулярная к плоскости. Признак перпендикулярности прямой и плоскости

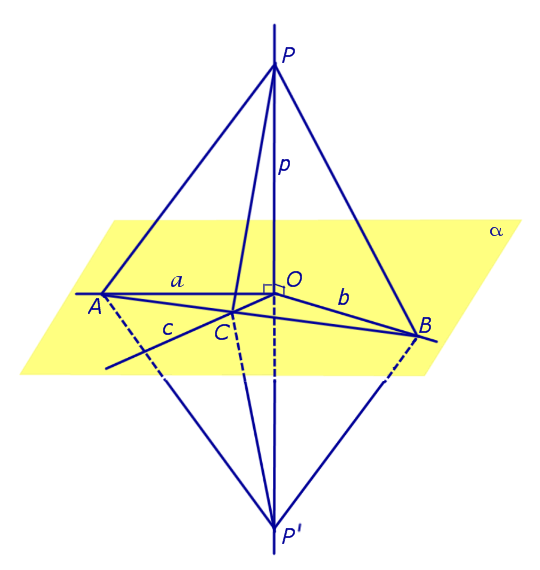
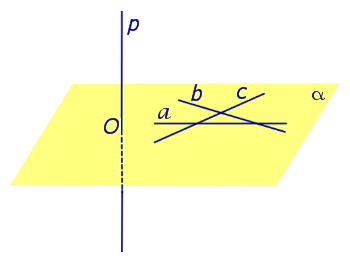
Определение . Прямой, перпендикулярной к плоскости , называют такую прямую, которая перпендикулярна к каждой прямой, лежащей на этой плоскости.

Признак перпендикулярности прямой и плоскости . Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в некоторой плоскости, то прямая перпендикулярна к этой плоскости.

Доказательство . Рассмотрим сначала следующий случай.

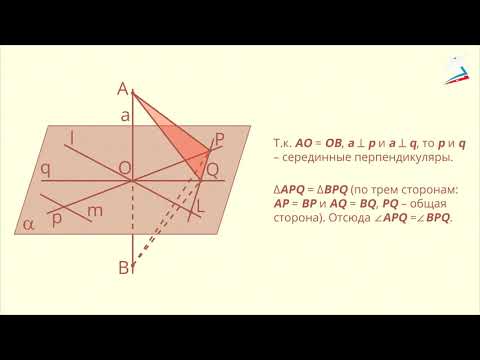
Предположим, что прямая p , пересекающая плоскость α в точке O, перпендикулярна к прямым a и b , лежащим на плоскости α и проходящим через точку O . Докажем, что в этом случае прямая p перпендикулярна любой другой прямой c , лежащей на плоскости α и проходящей через точку O .

С этой целью отметим на прямой a произвольную точку A , а на прямой b произвольную точку B (рис. 1).

Проведем прямую AB и обозначим буквой C точку пересечения прямых AB и c. Отметим на прямой p произвольную точку P и обозначим символом P’ точку, расположенную на прямой p так, чтобы точка O оказалась серединой отрезка PP’ . Поскольку прямые OA и OB являются серединными перпендикулярами к отрезку PP’ , то справедливы равенства

Из этих равенств, а также поскольку отрезок AB является общей стороной треугольников APB и AP’B , заключаем, что в силу признака равенства треугольников по трем сторонам трегольники APB и AP’B равны. Следовательно,

Отсюда в силу признака равенства треугольников по двум сторонам и углу между ними заключаем, что трегольник PBС равен треугольнику P’BС ( BP = BP’ , 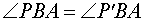, сторона BС — общая). Следовательно,

Таким образом, прямые PO и c перпендикулярны, что и требовалось доказать в рассматриваемом случае.

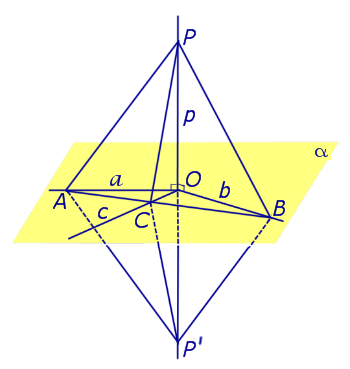
Теперь перейдем к общему случаю.

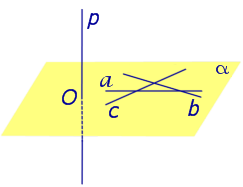
Предположим, что что прямая p , пересекающая плоскость α в точке O, перпендикулярна к прямым a и b , лежащим на плоскости α . Докажем, что в этом случае прямая p перпендикулярна любой другой прямой c , лежащей плоскости α (рис. 2).

С этой целью проведем через точку O прямые a’ , b’ и c’ соответственно параллельные прямым параллельные прямым a , b и c .

По определению угла между скрещивающимися прямыми прямая будет перпендикулярна прямым a’ и b’ , проходящим через точку O, и мы оказываемся в условиях уже рассмотренного случая.

Доказательство признака перпендикулярности прямой и плоскости завершено.

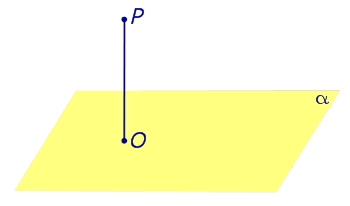
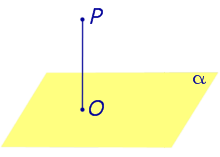
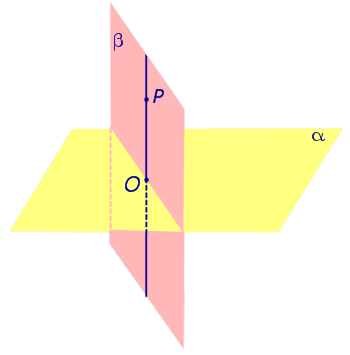
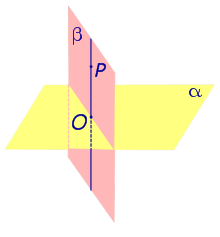
Замечание . Прямую, перпендикулярную к плоскости, часто называют перпендикуляром к плоскости. Точку перечения прямой, перпендикулярной к плоскости, с самой плоскостью называют основанием перпендикуляра.

Так, например, на рисунке 1 точка O является основанием перпендикуляра, опущенного из точки P на плоскость α .

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Свойства перпендикуляра к плоскости

Перечислим следующие свойства перпендикуляра к плоскости, доказательства которых мы оставляем читателю в качестве полезных упражнений.

Рисунок	Свойство
	Из любой точки можно опустить перпендикуляр на любую плоскость. Если точка O — основание перпендикуляра, опущенного из точки P на плоскость α , то длину отрезка PO называют расстоянием от точки P до плоскости α.
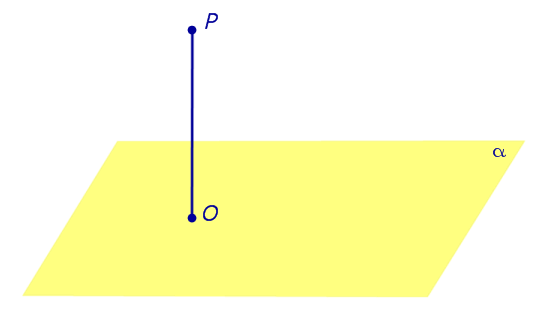
	Два любых перпендикуляра к плоскости параллельны
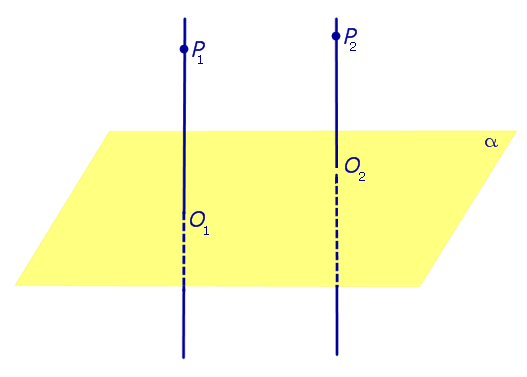
	Плоскости, перпендикулярные к одной прямой, параллельны.
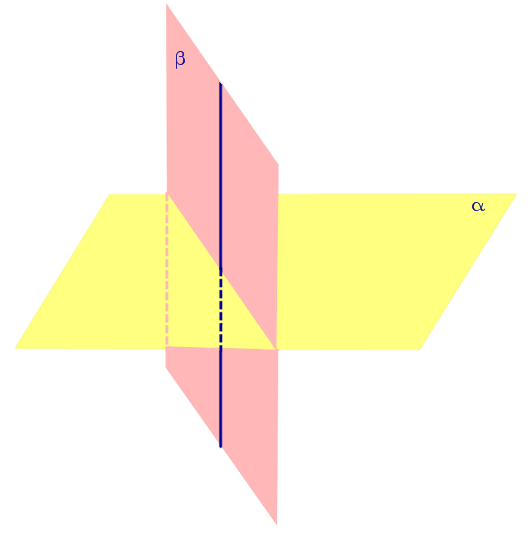	Если одна из плоскостей проходит через перпендикуляр к другой плоскости, то эти плоскости перпендикулярны.
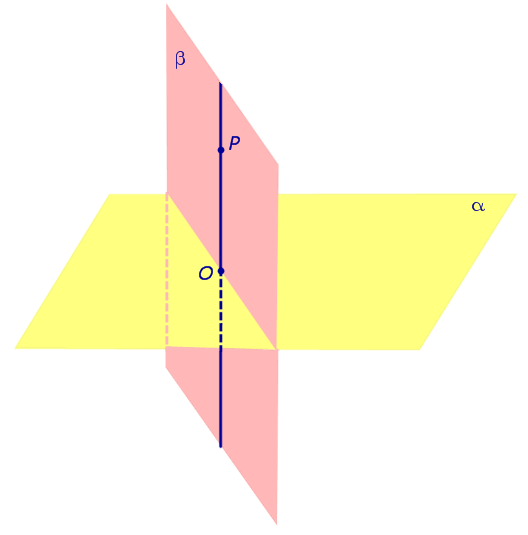	Если плоскости α и β перпендикулярны, а точка P лежит на плоскости β, то и перпендикуляр PO, опущенный из точки P на плоскость α , также лежит в плоскости β.

Свойство:
Из любой точки можно опустить перпендикуляр на любую плоскость. Если точка O — основание перпендикуляра, опущенного из точки P на плоскость α , то длину отрезка PO называют расстоянием от точки P до плоскости α.

Свойство:
Два любых перпендикуляра к плоскости параллельны параллельны

Свойство:
Плоскости, перпендикулярные к одной прямой, параллельны.

Свойство:
Если одна из плоскостей проходит через перпендикуляр к другой плоскости, то эти плоскости перпендикулярны.

Свойство:
Если плоскости α и β перпендикулярны, а точка P лежит на плоскости β, то и перпендикуляр PO, опущенный из точки P на плоскость α , также лежит в плоскости β.