Если прямая параллельна каждой из двух пересекающихся плоскостей то она параллельна их линии

Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Параллельные прямые

Параллельные прямые – прямые, которые лежат в одной плоскости и не пересекаются.

Признак параллельности прямых

Две прямые, параллельные третьей, параллельны между собой.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Параллельные прямая и плоскость

Прямая и плоскость называются параллельными , если они не имеют общих точек.

Признак параллельности прямой и плоскости

Если прямая, не принадлежащая данной плоскости, параллельна какой-нибудь прямой этой плоскости, то она параллельна этой плоскости.

Свойство прямой, параллельной данной плоскости

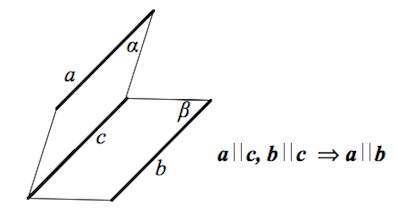
Если плоскость β проходит через прямую a , параллельную плоскости α , и пересекает эту плоскость по прямой b , то b || a .

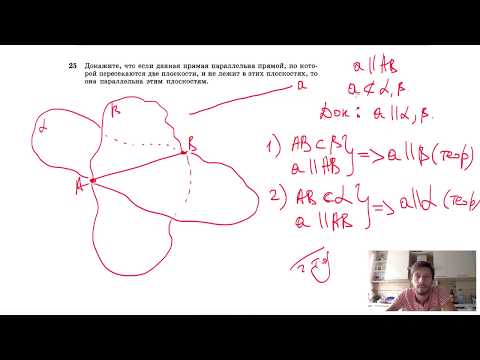
Видео:№25. Докажите, что если данная прямая параллельна прямой, по которой пересекаютсяСкачать

Параллельные плоскости

Параллельные плоскости – плоскости, которые не пересекаются.

Признаки параллельности плоскостей

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.

Если каждая из двух данных плоскостей параллельна третьей плоскости, то данные две плоскости параллельны между собой.

Свойства параллельных плоскостей

Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны.

Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Докажите, что если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна линии их пересечения?

Геометрия | 5 — 9 классы

Докажите, что если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна линии их пересечения.

Пусть это не так.

Очевидно, что прямая не может пересекать прямую пересечения плоскостей, так как в этом случае она не будет параллельна плоскостям.

Пусть они скрещиваются.

Через прямую, скрещивающуюся с данной можно провести только одну плоскость, параллельную данной прямой, значит, 2 плоскости совпадают.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Доказать, что если через каждую из двух параллельных прямых провести плоскости и они пересекаются , то линия пересечения параллельна каждой из них?

Доказать, что если через каждую из двух параллельных прямых провести плоскости и они пересекаются , то линия пересечения параллельна каждой из них.

Видео:Параллельность прямой к плоскостиСкачать

Докажите что все прямые пересекающие каждую из двух параллельных прямых лежат в одной плоскости?

Докажите что все прямые пересекающие каждую из двух параллельных прямых лежат в одной плоскости.

Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Плоскости Альфа и Бета пересекаются по прямой С?

Плоскости Альфа и Бета пересекаются по прямой С.

Плоскость Омега, параллельная прямой С, пересекает плоскости Альфа и Бета по прямым а и b соответственно.

Докажите, что a параллельна Бета и b параллельна Альфа.

Видео:Линия пересечения плоскостейСкачать

Плоскости a и в параллельны, причем плоскость а пересекает некоторую прямую а?

Плоскости a и в параллельны, причем плоскость а пересекает некоторую прямую а.

Докажите , что и плоскость в пересекает прямую а.

Видео:№57. Прямая а параллельна одной из двух параллельных плоскостей. Докажите, что прямаяСкачать

Докажите, что если плоскость проходит через прямую, параллельную другой прямой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна первой прямой?

Докажите, что если плоскость проходит через прямую, параллельную другой прямой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна первой прямой.

Видео:Параллельность прямых. 10 класс.Скачать

Докажите, что если прямая пар — на каждой из двух пересекающихся плоскостей, то она она параллельна линии их пересечания?

Докажите, что если прямая пар — на каждой из двух пересекающихся плоскостей, то она она параллельна линии их пересечания.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Помогите кто нибудь пожалуйста?

Помогите кто нибудь пожалуйста!

Докажите, что Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Докажите свойство линии пересечения двух параллельных плоскостей третьей плоскостью?

Докажите свойство линии пересечения двух параллельных плоскостей третьей плоскостью.

Видео:10 класс, 10 урок, Параллельные плоскостиСкачать

Верно ли утверждение : если одна из двух параллельных прямых параллельна плоскости, то вторая прямая не пересекает эту плоскость?

Верно ли утверждение : если одна из двух параллельных прямых параллельна плоскости, то вторая прямая не пересекает эту плоскость.

Видео:10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

Верно ли утверждение : если одна из двух прямых параллельна плоскости, а вторая пересекает эту плоскость, то прямые параллельны( и почему)?

Верно ли утверждение : если одна из двух прямых параллельна плоскости, а вторая пересекает эту плоскость, то прямые параллельны( и почему).

Вы зашли на страницу вопроса Докажите, что если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна линии их пересечения?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

AC иBD — это диагонали параллелограмма. Если они равны, то это прямоугольник. Сторона AD — это катет треугольника ABD. По теореме Пифагора : AD = КореньBD ^ 2 — AB ^ 2 = Корень289 — 64 = Корень225 = 15 Следовательно, площадь ABCD = AB * AD = 8 * 1..

Диагональ в основании АС. АС = √2 * а Высота СС1 = АС = √2 * а Диагональ ВС1 — по т. Пифагора. ВС = √((a² + (√2a)²) = √(3 * a²) = √3 * a — ОТВЕТ Рисунок по ссылке. Http : / / SSMaker. Ru / 42a57dc9.

График : парабола, ветки которой направлены вниз ; пересекает ось Ох при у = 0 ; 4х — х² = 0 ; х(4 — х) = 0 ; х1 = 0 ; х2 = 4. Значения 0 и 4 являются пределами интеграла По формуле Ньютона — Лейбница S = интеграл(4х — х²)dх = (4х² / 2 — х³ / 3) — (..

5. Дано : | Решение ABCD — парал — м, |ВС = AD(по св — вам парал — м) = >AD = 6 см ВС = 6см, | угол ABK = 180 — (90 + 30) = 60гр(т. К. BK | перпенд. Угол КАВ = 30 гр | угла В) = >BK = 1 / 2 AB = >2х2 = 4 см = AB ВК перпендикуляр угла В | = > СD = 4..

Ты какой класс 7 — — 8 — 9 — 10 — — 11.

S = a * a S = 1. 2 * 1. 2 = 1. 44 .

S = а * 4 s°12 * 4 = 56 ответ 56.

Sin(60°) = √3 / 2. Cos(60°) = 1 / 2. B = 46. A = 24. (b — a) / 2 = (46 — 24) / 2 = 11. C = 11÷1 / 2 = 22. P = 2•22 + 46 + 24 = 114.

150, 50, 10 всё очень легко.

Угол А + угол В = 62°, тогда угол МВА + угол ВАМ = 62° / 2 = 31°. Из треугольника АМВ : угол АМВ = 180° — 31° = 149°, поскольку самое углов треугольника равна 180°. Ответ : 149°.

Видео:10 класс, 17 урок, Признак перпендикулярности прямой и плоскостиСкачать

X класс: Тема I. Параллельность в пространстве (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3

Лемма о пересечении плоскости параллельными прямыми: Если одна из двух параллельных прямых пересекает плоскость, то вторая прямая также пересекает эту плоскость.

Доказать:

1. Проведем через прямые a и b плоскость p (рисунок 27). Сразу отметим, что плоскости p и a не совпадают (если бы они совпадали, то прямая a лежала бы в плоскости a, что противоречит условию).

2. Т. к. у несовпадающих плоскостей a и p есть общая точка A (A Î a по условию, A Î p по построению), Þ по аксиоме А3 a Ç p = l: A Î l.

3. По теореме о существовании и единственности прямой, параллельной данной, через точку A проходит единственная прямая, параллельная b; а это по условию прямая a. Следовательно, l  b, а т. к. прямые l и b лежат в одной плоскости, Þ l Ç b = ! B.

4. B Î l Ì a, B Î b, Þ B – общая точка прямой b и плоскости a. Значит, прямая b либо лежит в плоскости a, либо пересекает ее в точке B. Если b Ì a, то через прямую b и не лежащую на ней точку A проходят 2 несовпадающие плоскости p и a, что невозможно. А значит, b Ç a = ! B. #

Пользуясь доказанной леммой, докажем теорему о параллельности трех прямых:

Теорема о параллельности трех прямых: Две прямые, параллельные третьей прямой, параллельны между собой.

Доказать: a÷çb.

1. Сразу заметим, что прямые a и b не имеют общих точек: если бы у них была общая точка, то через нее проходили бы сразу 2 прямые, параллельные c, что невозможно по теореме о существовании и единственности прямой, параллельной данной.

2. Выберем на прямой b произвольную точку B и проведем плоскость a = (a; B) (рисунок 28). Т. к. т. B Î b, B Î a, Þ прямая b имеет общую точку B с плоскостью a, т. е. прямая b либо пересекает плоскость a, либо лежит в ней. Докажем, что b Ì a.

3. Допустим, что b Ç a = ! B. b÷çc, Þ по лемме о пересечении плоскости параллельными прямыми c также пересекает плоскость a. А т. к. a÷çc, Þ по той же лемме прямая a пересекает плоскость a. Но по построению a Ì a. Пришли к противоречию, Þ предположение неверно, т. е. b Ì a.

4. Итак, прямые a и b лежат в одной плоскости a и не имеют общих точек (см. п. 1), Þ a÷çb по определению. #

Замечание: Теорему о параллельности трех прямых часто называют свойством транзитивности параллельности прямых.

6. Параллельность прямой и плоскости

Напомним, что прямая a и плоскость a называются параллельными, если они не имеют общих точек: a÷ça Û a Ç a = Æ.

Замечание: Через точку, лежащую вне данной плоскости, можно провести бесконечно много прямых, параллельных данной плоскости (к примеру, всякая прямая, лежащая в плоскости потолка комнаты, параллельна плоскости ее пола).

Докажем признак, позволяющий устанавливать параллельность прямой и плоскости.

Признак параллельности прямой и плоскости: Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то прямая и плоскость параллельны (рисунок 29).

Доказать: b÷ça.

Допустим, что b Ç a. Тогда по лемме о пересечении плоскости параллельными прямыми a Ç a (т. к. a÷çb). Пришли к противоречию с условием (a Ì a), Þ b÷ça. #

Сформулируем и докажем несколько элементарных утверждений о параллельности прямой и плоскости:

1. Если одна из двух пересекающихся плоскостей содержит прямую, параллельную второй плоскости, то эта прямая параллельна линии пересечения данных плоскостей (рисунок 30).

Доказать: a÷çl.

Поскольку прямые a и l лежат в одной плоскости a, они либо параллельны, либо пересекаются. Если бы они пересекались, прямая a имела бы общую точку с плоскостью b, что противоречит условию. Значит, a÷çl. #

Следствие: Если прямая a параллельна плоскости b, то в этой плоскости найдется бесконечно много прямых, параллельных a (через прямую a можно провести бесконечно много плоскостей, каждая из которых будет пересекать плоскость b по прямой, параллельной a).

2. Если через каждую из двух параллельных прямых проведена плоскость, и эти плоскости пересекаются, то линия пересечения плоскостей параллельна каждой из этих прямых (рисунок 31).

Доказать: a÷çl; b÷çl.

1. a÷çb Ì b; Þ по признаку параллельности прямой и плоскости a÷çb.

2. Плоскость a содержит прямую a, параллельную плоскости b, Þ по утверждению 1, a÷çl.

3. b÷ça÷çl, Þ по теореме о параллельности трех прямых, b÷çl. #

3. Если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна линии их пересечения (рисунок 32).

Доказать: с÷çl.

1. с÷ça; Þ по следствию из утверждения 1, в плоскости a найдется прямая a, параллельная c (рисунок 32). Аналогично $ b Ì b: с÷çb.

2. a÷çс÷çb, Þ по теореме о параллельности трех прямых, a÷çb.

4. c÷ça÷çl, Þ по теореме о параллельности трех прямых, с÷çl. #

7. Скрещивающиеся прямые

Как известно, две прямые, лежащие в одной плоскости, либо параллельны, либо пересекаются. Но оказывается, что не через всякие 2 прямые в пространстве можно провести плоскость. К примеру, через прямые, содержащие ребра AB и CC1 куба ABCDA1B1C1D1 нельзя провести плоскость (рисунок 33). Такие прямые называются скрещивающимися.

Две прямые называются скрещивающимися, если через них нельзя провести плоскость. Для скрещивающихся прямых a и b используется следующее обозначение: .

Замечание 1: Поскольку как через две пересекающиеся, так и через две параллельные прямые в пространстве можно провести плоскость, скрещивающиеся прямые не являются ни пересекающимися, ни параллельными. Таким образом, две прямые в пространстве могут быть либо пересекающимися, либо параллельными, либо скрещивающимися.

Замечание 2: Не следует ориентироваться на чертеж, устанавливая характер взаимного расположения двух прямых (к примеру, на рисунке 33 изображения прямых AB и CC1 пересекаются, в то время как сами прямые являются скрещивающимися).

Поскольку чертеж не позволяет доказать, что прямые являются скрещивающимися, а напротив, может создать иллюзию их пересечения, для доказательства того, что через две данные прямые нельзя провести плоскость, используется следующий признак скрещивающихся прямых: Если одна из двух прямых лежит в некоторой плоскости, а вторая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то данные прямые являются скрещивающимися.

Доказать: .

1. Допустим, что через прямые a и b можно провести плоскость b. Тогда т. B Î b Ì b, Þ плоскость b проходит через прямую a и не лежащую на ней точку B. Но т. к. плоскость a также содержит прямую a и точку B, плоскости a и b совпадают.

2. b Ì b º a, Þ b Ì a, что противоречит условию. Значит, предположение неверно, т. е. через прямые a и b нельзя провести плоскость Û . #

С помощью сформулированного только что признака легко доказать, к примеру, что прямые AB и CC1 на рисунке 33 – скрещивающиеся: Þ .

Замечание: Если в задаче идет речь о скрещивающихся прямых, не «привязанных» к какой-либо геометрической конструкции, удобно изображать их на чертеже в виде противоположных ребер тетраэдра (на рисунке 35 , поскольку a Ì (ABC), b Ç (ABC) = ! C Ï a).

Оказывается, что каковы бы ни были две скрещивающиеся прямые, через каждую из них можно провести плоскость, параллельную второй прямой. Это утверждает следующая теорема:

Теорема о существовании и единственности плоскости, параллельной данной прямой: Через каждую из двух скрещивающихся прямых можно провести единственную плоскость, параллельную второй прямой.

.

Доказать:

$: 1. Возьмем произвольную т. B Î b и проведем через нее прямую a¢÷ça (рисунок 36; это можно сделать согласно теореме о существовании и единственности прямой, параллельной данной).

2. Проведем через пересекающиеся прямые a¢ и b плоскость a (это можно сделать согласно теореме о задании плоскости двумя пересекающимися прямыми).

3. a – искомая плоскость: a÷ça¢ Ì a, Þ по признаку параллельности прямой и плоскости, a÷ça; b Ì a по построению.

!: 4. Допустим, что через прямую b можно провести еще одну плоскость p, параллельную a. Тогда т. к. B Î b Ì p, B Î a¢, Þ прямая a¢ имеет с плоскостью p как минимум одну общую точку B. Следовательно, прямая a¢ либо лежит в плоскости p, либо пересекает ее в точке B.

5. Если a¢ Ç p = ! B, то поскольку a¢÷ça, прямая a также пересекает плоскость p по лемме о пересечении плоскости параллельными прямыми. Это противоречит тому, что a÷çp, Þ a¢ Ì p.

6. Т. к. a¢ Ì p, то плоскость p проходит через пересекающиеся прямые a¢ и b, а значит, совпадает с плоскостью a по теореме о задании плоскости двумя пересекающимися прямыми. Следовательно, a – единственная.

7. Аналогично можно доказать, что $ ! b÷çb: a Ì b. #

8. Угол между прямыми

Напомним, что углом между пересекающимися прямыми называется наименьший из четырех углов, образованных при их пересечении, а угол между параллельными прямыми считается равным нулю. Дадим определение угла между скрещивающимися прямыми.

Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным прямым и проведенными через произвольную точку O пространства (на рисунке 37 Ð(a, b) = Ð(a¢, b¢)). Можно доказать, что величина угла между прямыми не зависит от выбора точки O, через которую проводятся параллельные им прямые. В частности, можно провести прямую через произвольную точку одной прямой параллельно второй прямой (на рисунке 37 через точку C прямой b проведена прямая a²÷ça, и Ð(a, b) = Ð(a², b)).

Из определения угла между прямыми следует, что он может лежать в пределах [0; 90°]. Две прямые в пространстве (не обязательно пересекающиеся), угол между которыми равен 90°, называются перпендикулярными. Позже понятие перпендикулярных прямых будет рассмотрено подробнее.

9. Параллельность плоскостей

Напомним, что две плоскости называются параллельными, если они не имеют общих точек.

Замечание: Из определения параллельных плоскостей следует, что всякая прямая, лежащая в одной из двух параллельных плоскостей, параллельна второй плоскости.

Докажем признак параллельности двух плоскостей: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Доказать: a÷çb.

1. a÷ça¢ Ì b, Þ прямая a либо принадлежит плоскости b, либо параллельна ей по признаку параллельности прямой и плоскости. Аналогично прямая b либо принадлежит плоскости b, либо параллельна ей.

2. Если a Ì b (рисунок 38а), то a = a Ç b, Þ M Î a Ì b, Þ прямая b имеет с плоскостью b общую точку M. Но из п. 1 прямая b либо лежит в плоскости b, либо параллельна ей, а поскольку она имеет с плоскостью b общую точку M, Þ b Ì b. Но тогда b = a Ç b = a, т. е. прямые a и b совпадают, что противоречит условию. Значит, a Ë b, т. е. a÷çb. Аналогично b÷çb.

3. Допустим, что плоскости a и b непараллельны; тогда по аксиоме А3 a Ç b = m (рисунок 38б). , Þ согласно утверждению 1 о параллельности прямой и плоскости, a÷çm (эти прямые лежат в одной плоскости a и не могут пересекаться, т. к. прямая a не имеет общих точек с плоскостью b). Аналогично b÷çm. Получилось, что через точку M проходят сразу 2 прямые, параллельные m, что противоречит теореме о существовании и единственности прямой, параллельной данной. Следовательно, предположение неверно, т. е. a÷çb. #

Параллельные плоскости обладают следующими свойствами:

1. (Теорема о линиях пересечения параллельных плоскостей третьей плоскостью): Если две параллельные плоскости пересечены третьей плоскостью, то их линии пересечения параллельны (рисунок 39).

Доказать: a÷çb.

Прямые a и b лежат в одной плоскости p, Þ они либо параллельны, либо пересекаются. Если они пересекаются, то у плоскостей a и b есть общая точка, что противоречит условию. Значит, a÷çb. #

2. (Теорема о пересечении параллельных плоскостей прямой): Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и вторую плоскость.

Доказать: l Ç b = ! B.

1. Выберем в плоскости b произвольную точку C Ï l и проведем плоскость p = (l; C) (рисунок 40).

2. Плоскости p и a имеют общую точку A, Þ по аксиоме А3, p Ç a = a: A Î a.

3. Плоскости p и b имеют общую точку C, Þ по аксиоме А3 p Ç b = b: C Î b.

4. По свойству 1 параллельных плоскостей, a÷çb. В плоскости p l Ç a = A, a÷çb; Þ l Ç b = B.

5. B Î b Ì b, B Î l, Þ B – общая точка прямой l и плоскости b, Þ прямая l либо лежит в плоскости b, либо пересекает ее в точке B. Если бы l Ì b, то у плоскостей a и b была бы общая точка A, что противоречит условию. Значит, l Ç b = ! B. #

3. (Теорема о пересечении параллельных плоскостей третьей плоскостью): Если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и вторую плоскость.

Доказать: p Ç b = b.

1. Проведем в плоскости p произвольную прямую l, пересекающую a: l Ç a = A (рисунок 41). Тогда A Î a Ì a, A Î l, Þ l Ç a = A.

2. По предыдущему свойству l Ç b = B; Þ B Î l Ì p, B Î b, Þ у плоскостей p и b есть общая точка B. Значит, по аксиоме А3, p Ç b = b. #

4. (Теорема об отрезках параллельных прямых, заключенных между параллельными плоскостями): Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

Доказать: A1A2 = B1B2.

1. Проведем через параллельные прямые a и b плоскость p (рисунок 42). Согласно аксиоме А3, p Ç a = A1B1, p Ç b = A2B2.

2. По свойству 1 параллельных плоскостей, A1B1÷çA2B2; по условию A1A2÷çB1B2; Þ A1A2B2B1 – параллелограмм; Þ по свойству параллелограмма, A1A2 = B1B2. #

Докажем теорему о существовании и единственности плоскости, параллельной данной: Через точку, не принадлежащую данной плоскости, можно провести единственную плоскость, параллельную данной.

Доказать:

$: 1. Выберем в плоскости a произвольную точку A и проведем через нее прямые a Ì a и b Ì a (рисунок 43).

2. Проведем через точку M прямые a1÷ça и b1÷çb (это можно сделать по теореме о существовании и единственности прямой, параллельной данной).

3. Через пересекающиеся прямые a1 и b1 проведем плоскость b. Эта плоскость – искомая: M Î a1 Ì b по построению; b÷ça по признаку параллельности плоскостей.

!: 4. Допустим, что через точку M проходит еще одна плоскость g÷ça. Поскольку плоскости b и g имеют общую точку M, они пересекаются. Но т. к. a÷çg, g Ç b, Þ по теореме о пересечении параллельных плоскостей третьей плоскостью, a Ç b, что противоречит условию. Значит, плоскость b – единственная. #

Следствие (теорема о транзитивности параллельности плоскостей): Две плоскости, параллельные третьей, параллельны между собой.

Доказательство: Пусть b÷ça, g÷ça. Если предположить, что b  g, то у плоскостей b и g есть общая точка, а значит, через эту точку проходят сразу 2 плоскости b и g, параллельные a, что противоречит доказанной только что теореме. Следовательно, b÷çg. #

Докажем теорему о существовании и единственности пары параллельных плоскостей, проходящих через две скрещивающиеся прямые: Через всякую пару скрещивающихся прямых можно провести единственную пару параллельных плоскостей.

.

Доказать:

$: 1. Выберем на прямой a произвольную точку A и проведем через нее прямую b1÷çb (рисунок 44а).

2. Проведем через пересекающиеся прямые a и b1 плоскость a. Тогда по признаку параллельности прямой и плоскости, b÷ça.

3. Выберем на прямой b произвольную точку B и проведем через нее плоскость b÷ça (это можно сделать по теореме о существовании и единственности плоскости, параллельной данной).

4. Допустим, что b Ç b = ! B. Тогда b Ç a по теореме о пересечении параллельных плоскостей прямой, что противоречит п.2. Значит, b Ì b.

5. Плоскости a и b – искомые: a Ì a по построению (п. 2), b Ì b (п. 4), a÷çb по построению (п. 3).

!: 6. Допустим, что через прямые a и b можно провести еще одну пару параллельных плоскостей a¢ и b¢: a Ì a¢, b Ì b¢: a¢÷çb¢ (рисунок 44б).

7. Проведем плоскость p = (b; A). Тогда т. к. b Ì b¢, b Ì p, Þ p Ç b¢ = b.

8. Þ по свойству параллельных плоскостей, p Ç a¢ = b¢÷çb: A Î b¢ (т. к. A Î p, A Î a Ì a¢). Но т. к. через т. A можно провести единственную прямую, параллельную b, то прямые b¢ и b1 совпадают, т. е. p Ç a¢ = b1.

9. Þ плоскость a¢ проходит через пересекающиеся прямые a и b1. Но т. к. через две пересекающиеся прямые можно провести! плоскость, то a¢ º a.

10. Т. к. плоскости a¢ и a совпадают, то через прямую b проходят сразу 2 плоскости b и b¢, параллельные a. Значит, и через точку B проходят 2 плоскости, параллельные a, что противоречит теореме о существовании и единственности плоскости, параллельной данной. Следовательно, предположение неверно, т. е. пара плоскостей a и b – единственная. #

10. Дальнейшие сведения о многогранниках

📹 Видео

6. Параллельность прямой и плоскостиСкачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ 10 класс стереометрияСкачать

Параллельность прямых, плоскостей, прямой и плоскости | Математика ЕГЭ для 10 класса | УмскулСкачать