Попадание точки в заданную область окружности

Program N26 (Input, Output);

Объявление имени программы

Блок объявления меток: задаем метки 1 и 2

Блок объявления глобальных переменных

Переменные X и Y — абсцисса и ордината проверяемой точки

Переменная R — радиус окружности

Начало тела программы

WriteLn (‘PASCAL: Проверка попадания точки в окружность.’);

Формулировка цели алгоритма

Write (‘Введите радиус окружности: R = ‘);

Запрос ввода R — радиуса окружности

Write (‘Введите абсциссу точки: X = ‘);

Запрос ввода X — абсциссы точки

Write (‘Введите ординату точки: Y = ‘);

Запрос ввода Y — ординаты точки

Если точка (X,Y) принадлежит окружности радиуса R, то переход на метку 1

WriteLn (‘Точка (‘, X, ‘,’, Y, ‘) не попала в окружность радиуса R = ‘, R);

Вывод сообщения о НЕпопадании точки (X,Y) в заданную окружность радиуса R

Переход на метку 2

1: WriteLn (‘Точка (‘, X, ‘,’, Y, ‘) попала в окружность радиуса R = ‘, R);

Метка 1: Вывод сообщения о попадании точки (X,Y) в задан. окружность радиуса R

Метка 2: ожидание нажатия клавиши Enter для завершения

(с) Все права защищены.

По всем интересующим вопросам прошу писать электронный адрес

Видео:33 Задача: Принадлежит ли точка кругу с центром в начале координат?Скачать

Алгоритм определения попадания точки в контур на основе комплексного анализа

Привет всем Хабра людям. Хочу представить уважаемым читателям пример, когда сухая и далекая от жизни в нашем понимании высшая математика дала не плохой практический результат.

Сначала немного воспоминаний

Было это в бытность мою студентом одного из технических Вузов в 90-е, курсе наверно втором. Попал я как-то на олимпиаду по программированию. И вот на этой самой олимпиаде и было задача: задать координаты треугольника, тестовой точки на плоскости, и определить принадлежит ли эта точка области треугольника. В общем, плевая задачка, но тогда я ее так и не решил. Но после задумался – над более общей задачей – принадлежность полигону. Повторюсь – была середина 90 –х, интернета не было, книжек по компьютерной геометрии не было, а были лекции по вышке и лаборатория 286 –х с турбо паскалем. И вот так совпали звезды, что как раз в то время когда я размышлял над проблемой, на вышке нам читали теорию комплексного переменного. И одна формула (о ней ниже) упала на благодатную почву. Алгоритм был придуман и реализован на паскале (к сожалению мой полутора гиговый винт погиб и унес в небытие этот код и кучу других моих юношеских наработок). После института я попал работать в один НИИ. Там мне пришлось заниматься разработкой ГИС для нужд работников института и собственной одной из задачей было определение попадания объектов в контур. Алгоритм был переписан на С++ и отлично зарекомендовал себя в работе.

Задача для алгоритма

Определить:

принадлежит ли точка области D, ограниченной полигоном.

Вывод формул для последующего написания алгоритма ни в коем случае не претендует на математическую полноту и точность, а лишь демонстрирует инженерный (потребительский подход) к Царице полей наук.

Интегральная формула Коши

Пояснение с рабоче-крестьянской инженерной точки зрения:
— граница Г наш заданный контур,
— z0 -тестируемая точка
— f(z) — комплексная функция от комплексного аргумента нигде в контуре не обращается в бесконечность.

Те есть, чтобы установить принадлежность точки контуру, нам необходимо вычислить интеграл и сравнить его со значением функции в данной точки. Если они совпадают, то точка лежит в контуре. Замечание: интегральная теорема коши гласит, что если точка не лежит в контуре, те подынтегральное выражение нигде не обращается в бесконечность, то интеграл равен нулю. Это упрощает дело – нужно лишь вычислить интеграл и проверить его на равенство нулю: равен нулю точка не контура, отличен — лежит в контуре.
Займемся вычислением интеграла. За f(z) примем простую функцию 1. Не нарушая общности можно за z0 принять точку 0 (всегда можно сдвинуть координаты).

Избавляемся от мнимой единицы в знаменателе подынтегральной части и расщепим интеграл на действительную и мнимую части:

Получилось два криволинейных интеграла II рода.
Вычислим первый

Выполнятся условие не зависимости интеграла от пути, следовательно, первый интеграл равен нулю и его вычислять не нужно.

С мнимой частью такой фокус не проходит. Вспоминаем, что наша граница состоит из отрезков прямых, получаем:

Где Гi- это отрезок (xi,yi)- (xi+1,y i+1)
Вычислим i-ый интеграл. Для этого запишем уравнение i-го отрезка в параметрическом виде

Подставим в интеграл

и после громоздких и нудных преобразований получим следующую прельстивую формулу:

Окончательно получаем

Алгоритм на C++:

T – тип точки, например:
struct PointD
<
double x,y;
>;

Пример

Пример работы алгоритма написан с применением самой на мой взгляд великой библиотеки 2D графики:Anti-Grain Geometry (AGG) .

Управление:
клик левой кнопкой – добавление новой точки контура
правой кнопкой — замыкание контура
левой с зажатым Shift-ом – перенос тестовой точки

Господа, кому интересно, привожу более быстрый алгоритм. Уже не мой.
Отдельное и огромное спасибо forgotten за статейку.
template bool pt_in_polygon2(const T &test,const std::vector &polygon)
<

static const int q_patt[2][2]= < , >;

Видео:Попадание точки в заданную область. Круг в круге. Уроки программирования на С++.Скачать

Язык Pascal: решение задач на попадание точки в заданную область

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Попадание точки в заданную область. Два сектора. Уроки программирования на С++.Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Решение задач на попадание точки в заданную область

Примеры задач №1. Написать программу, которая определяет, попала ли точка с заданными координатами (вводятся пользователем) в заштрихованную область. Попадание на границу считаем попаданием в область.

Примеры задач Составим блок-схему к этой задаче: Начало Ввод х, у Да Точка попадает в область Точка не попадает в область Да Нет Нет Конец

Примеры задач Запишем теперь программу. 1 способ – использование составного условия var x, y: real; begin readln(x,y); if (y>=-x+1)and(sqr(x)+sqr(y) =-x+1 then writeln(‘Точка попадает в область’) else writeln(‘Точка не попадает в область’); end. Какая ошибка допущена в программе? Подберите примеры координат точек, при которых программа будет работать неверно. Как исправить программу?

Примеры задач №2. Написать программу, которая определяет, попала ли точка с заданными координатами (вводятся пользователем) в заштрихованную область. Попадание на границу считаем попаданием в область.

Примеры задач Данную область можно представить как объединение двух областей A и B. Составим условия. Допишите программу самостоятельно.

Упражнения №1. Требовалось написать программу, которая вводит с клавиатуры координаты точки на плоскости (х, у – действительные числа) и определяет принадлежность точки заштрихованной области. Программист торопился и написал программу неправильно. var x, y:real; begin readln(x,y); if x*x+y*y>4 then if y>=-2 then if y =x*x-2 then write(‘Принадлежит’) else write(‘Не принадлежит’); end. В областях A, B, C, E1, E2, F не включаются границы закрашенной области D. Последовательно выполните следующее. 1. Перерисуйте и заполните таблицу, которая показывает, как работает программа при аргументах, принадлежащих разным областям (A,B,C,D,E,F) Область y =x*x-2 Программа выведет Область обрабатывается верно A B C D E1 E2 F

Упражнения №2. Требовалось написать программу, которая вводит с клавиатуры координаты точки на плоскости (х, у – действительные числа) и определяет принадлежность точки заштрихованной области. Программист торопился и написал программу неправильно. var x,y:real; begin readln(x,y); if y =x*x-2 then write(‘Принадлежит’) else write(‘Не принадлежит’); end. В областях A, B, C, E1, E2, F не включаются границы закрашенной области D. 2. Укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы.

Домашнее задание 1.https://informatics.mccme.ru/mod/statements/view3.php?chapterid=112169#1 2.https://informatics.mccme.ru/mod/statements/view3.php?chapterid=112172#1 3.https://informatics.mccme.ru/mod/statements/view3.php?id=16730&chapterid=112171#1

Использованные источники 1. Информатика: пособие для подготовки к ЕГЭ/ Е. Т. Вовк [и др.]; под ред. Е. Т. Вовк. – М.: БИНОМ. Лаборатория знаний, 2013. – 322 с.

📺 Видео

Алгоритмы. Попадание точки в кругСкачать

Попадание точки в заданную область на числовой прямой. Уроки программирования на С++.Скачать

Попадание точки в заданную область. Первая координатная четверть. Уроки программирования на С++.Скачать

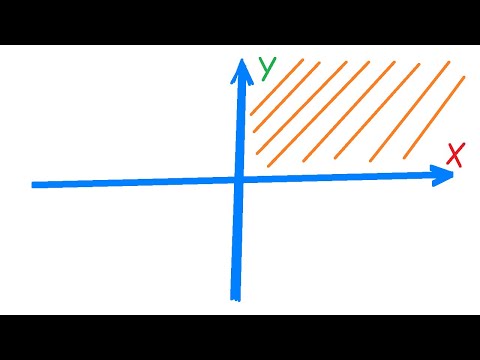
Программирование на С++. Урок 11. Попадает ли точка в заштрихованную область 2.Скачать

Программирование на С++. Урок 10. Попадает ли точка в заштрихованную областьСкачать

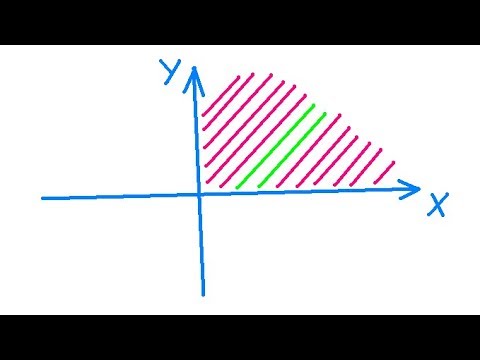
Определить принадлежит ли точка области Д371Скачать

Алгоритмы развётвлённой структуры в С++. If, Else. Лабораторная работа №2. Попадёт ли точка?Скачать

Практика 2 (Компьютерное задание 2 "Попадание точки в область")_Эз-16,17 группыСкачать

Алгоритмы. Попадание точки в треугольникСкачать

Определить принадлежность точки Д310Скачать

Условие принадлежности четырёх точек одной окружностиСкачать

Консультация к ЛР2 Параметрический цикл и ветвление в PythonСкачать

Определить принадлежность точки к области окружности Д390Скачать

Математика без Ху!ни. Непрерывность функции, точки разрыва.Скачать

Алгоритмы. Пересечение окружностейСкачать

Как найти координаты точек на тригонометрической окружностиСкачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать