Если прямая не пересекает одну из двух параллельных прямых то другую

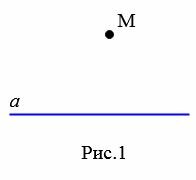
Рассмотрим прямую a и точку M, не лежащую на этой прямой (Рис.1). Докажем, что через точку M можно провести прямую, параллельную прямой a.

Проведем через точку M прямую c, перпендикулярно прямой a, и прямую b, перпендикулярно прямой c (Рис.2).

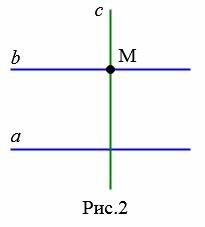Поскольку a и b перпендикулярны прямой с, то они параллельны (статья Перпендикулярные прямые Теорема 1 и статья Параллельные прямые. Признаки параллельности прямых Определение 1). Таким образом через точку M проходит прямая, параллельная прямой a.

Возникает вопрос, существует ли другая прямая, проходящая через точку M параллельно прямой a. Интуитивно ясно, что если немного повернуть прямую b вокруг оси M, то прямые b и a пересекутся. Но доказать это утверждение до сих пор не удалось. основываясь на стальных аксиомах геометрии.

Таким образом имеем это утверждение в виде аксиомы:

Аксиома 1. Через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.

Следствие 1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

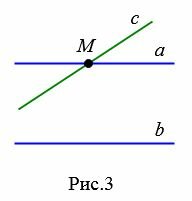Доказательство. Пусть заданы параллельные прямые a и b и пусть прямая c пересекает a в точке M (Рис.3). Докажем, что прямая c пересекает и прямую b.

Предположим обратное, т.е. c не пересекает b. Тогда получается, что через точку M проходят две прямые a и c параллельно прямой b, что невозможно (Аксиома 1). Следовательно прямая с пересекает и прямую b.

Следствие 2. Если две прямые параллельны третьей прямой, то они параллельны.

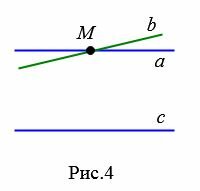Действительно. Предположим, что прямые a и b параллельны прямой c. Докажем, что прямая a параллельна прямой b. Предположим обратное, т.е. прямые a и b пересекаются в точке M (Рис.4). Тогда получается, что через точку M проходят две прямые, параллельные прямой c. Но это невозможно (Аксиома 1). Значит прямые a и b параллельны.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Геометрия. 7 класс

Конспект урока

Аксиома параллельных прямых

Перечень рассматриваемых вопросов:

• Аксиомы и теоремы.
• Исторические сведения об аксиоматическом построении евклидовой геометрии.
• Параллельные и перпендикулярные прямые.
• Признаки параллельности прямых.
• Решение задач на доказательство параллельности прямых.

Аксиома – это утверждение, которое принимается в качестве исходного, без доказательства в рамках данной теории.

Аксиома параллельных прямых.

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Следствия из аксиомы.

Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Если две прямые, параллельны третьей прямой, то они параллельны.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

1. Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
2. Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
3. Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
4. Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
5. Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения

Геометрия на плоскости изучает фигуры: сначала даются их определения, затем доказываются свойства или отношения в виде теорем.

Однако есть утверждения, которые принимаются в качестве исходных, они не доказываются. Это аксиомы.

Аксиома – происходит от греческого «аксиос», что означает «ценный, достойный». Изначально имело смысл «самоочевидная истина».

Теорема – греческое слово, означает «зрелище, представление». В математике греков употреблялось в смысле «истина, доступная созерцанию».

Аксиома параллельных прямых.

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Следствия из аксиомы.

Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Если две прямые параллельны третьей прямой, то они параллельны.

Впервые аксиоматический подход к изложению геометрии был изложен в знаменитом сочинении Евклида «Начала» в III веке до нашей эры. Геометрию, которую мы изучаем, по сей день, называют евклидовой. Схема изучения геометрии представлена так: задаются начальные понятия (точка, прямая, плоскость), определения фигур (отрезок, луч, треугольник и др.). Затем изучаются свойства или отношения между ними в виде аксиом или теорем.

Приведём примеры аксиом, которые уже встречали в предыдущих параграфах, хотя они не назывались аксиомами.

• Через любые две точки проходит прямая, и притом только одна.
• На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
• От любого луча можно отложить угол, равный данному неразвёрнутому углу, и притом только один.

Евклид является автором аксиоматического подхода к построению геометрии.

Аксиома параллельных прямых:

через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

На рисунке через точку М проведены две прямые. Но только одна из них прямая b параллельна прямой а.

Утверждения, которые выводятся из аксиом или теорем, называются следствиями, и они доказываются.

Следствия из аксиомы параллельных прямых.

1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Доказательство методом от противного.

Пусть a ║b, c пересекает прямую a в точке M. Предположим, что прямая c не пересекает b. Тогда через точку M проходит две прямые a и c параллельные b. Это противоречит аксиоме, значит предположение неверно, т. е. прямая c пересекает b.

2. Если две прямые параллельны третьей прямой, то они параллельны.

Доказательство методом от противного.

Пусть a ║ c, b ║ c.

Предположим, что прямые a и b не параллельны, т. е. пересекаются в точке M. Тогда через точку M проходит две прямые a и b параллельные c. Это противоречит аксиоме, значит, предположение неверно, т. е. прямая a параллельна прямой b.

Разбор заданий тренировочного модуля

№ 1. Доказать существование прямой, параллельной данной.

1. Проведём через точку М прямую c ┴ а.
2. Затем проведём прямую b ┴ c.
3. Так как прямые a и b перпендикулярны прямой c, то они параллельны.

№ 2. Через точку А, не лежащую на прямой р, проведены четыре различные прямые.

Сколько из них пересекает прямую р?

1 случай. Если одна из прямых параллельна р. Тогда три других пересекают прямую р, согласно следствию 1 из аксиомы параллельных прямых.

2 случай. Если ни одна из прямых не параллельна р. Тогда все четыре пересекают прямую р.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Тест по геометрии (теоретический) «Признаки параллельности прямых»

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Тест. Параллельные прямые (теоретический).

A1. Две прямые на плоскости называются параллельными, если они:

1) перпендикулярны одной прямой

2) находятся на одинаковом расстоянии друг от друга

3) не пересекаются на данном чертеже

4) не пересекаются

А2. Один из признаков параллельности двух прямых гласит:

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

Если при пересечении двух прямых секущей сумма соответственных углов равна 180°, то прямые параллельны

Если при пересечении двух прямых секущей односторонние углы равны, то прямые параллельны

Если при пересечении двух прямых секущей вертикальные углы равны, то прямые параллельны

А3. Выберите утверждение, являющееся аксиомой параллельных прямых:

Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной

Если прямые параллельны третьей прямой, то они параллельны

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны

А4. Если две параллельные прямые пересечены секущей, то:

Сумма накрест лежащих углов равна 180°

Соответственные углы равны

Вертикальные углы равны

Односторонние углы равны

А5. Если прямая перпендикулярна одной из двух параллельных прямых, то:

Другую прямую она не пересекает

Другой прямой она параллельны

Она перпендикулярна и другой

С другой прямой она совпадает

А6. Всякая теорема состоит из нескольких частей:

Условия и заключения

Того, что дано, того, что требуется доказать, и доказательства

Условия, заключения и доказательства

Условия и доказательства

А7. При пересечении двух прямых секущей образуются углы, имеющие специальные названия:

Смежные и вертикальные

Острые, прямые, тупые

Параллельные и перпендикулярные

Накрест лежащие, соответственные, односторонние

А8. Аксиома – это:

Положение геометрии, требующее обоснований

Положение геометрии, не требующее доказательства

Положение геометрии, имеющее следствие

Положение геометрии, обратное к которому верно

А9. Выберите утверждение, которое является признаком параллельности прямых:

При пересечении двух параллельных прямых секущей, накрест лежащие углы равны

Если при пересечении двух прямых секущей односторонние углы равны, то прямые параллельны

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

Если при пересечении двух прямых секущей сумма соответственных углов равна 180°, то прямые параллельны

А10. Если прямая не пересекает одну из двух параллельных прямых, то:

Другую прямую она тоже не пересекает

Другую прямую она пересекает

Другой прямой она перпендикулярна

С другой прямой она совпадает

Тест. Параллельные прямые (теоретический).

А1. Два отрезка на плоскости называются параллельными, если они:

Их концы находятся на одинаковом расстоянии друг от друга

Лежат на параллельных прямых

Перпендикулярны одному отрезку

А2. Один из признаков параллельности двух прямых гласит:

Если при пересечении двух прямых секущей сумма смежных углов равна 180°, то прямые параллельны

Если при пересечении двух прямых секущей сумма накрест лежащих углов равна 180°, то прямые параллельны

Если при пересечении двух прямых секущей односторонние углы равны, то прямые параллельны

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны

А3. Выберите утверждение, являющееся следствием из аксиомы параллельных прямых

Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую

Если при пересечении двух прямых секущей вертикальные углы равны, то прямые параллельны

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

А4. Если две параллельные прямые пересечены секущей, то:

Сумма смежных углов равна 180°

Накрест лежащие углы равны

Вертикальные углы равны

Сумма соответственных углов равна 180°

А5. Если прямая пересекает одну из двух параллельных прямых, то:

С другой прямой она совпадает

Другой прямой она параллельна

Другой прямой она перпендикулярна

Она пересекает и другую

А6. Обратной данной, называется теорема, в которой:

Условие и заключение являются обратными

Теорема доказывается методом от противного

Условием является заключение данной теоремы, а заключением- условие данной теоремы

Доказывается, что такого быть не может

А7. Прямая c является секущей к прямым a и b, если:

Она пересекает каждую из них в одной точке

Она пересекает хотя бы одну из них

Перпендикулярна каждой из них

Перпендикулярна хотя бы одной из них

А8. Что общего между аксиомой и теоремой? Аксиома и теорема:

Представляют собой составные части геометрии

Всегда имеют следствие

А9. Выберите утверждение, которое является свойством параллельных прямых:

При пересечении двух параллельных прямых секущей сумма накрест лежащих равна 180°

При пересечении двух параллельных прямых секущей сумма односторонних углов равна 180°

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны

Если при пересечении двух прямых секущей сумма соответственных углов равна 180°, то прямые параллельны

А10. Если прямая неперпендикулярная к одной из двух параллельных прямых, то:

К другой прямой она не параллельна

К другой прямой она параллельна

Она неперпендикулярная и к другой

К другой прямой она может быть перпендикулярна

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 341 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 691 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Титова Надежда НиколаевнаНаписать 9030 23.03.2020

Номер материала: ДБ-1070265

18.03.2020 10

15.03.2020 14

15.03.2020 17

11.03.2020 31

26.02.2020 121

21.02.2020 19

17.02.2020 62

04.02.2020 37

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Названы главные риски для детей на зимних каникулах

Время чтения: 3 минуты

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Россия направит $10,3 млн на развитие школьного питания в нескольких странах

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📹 Видео

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Параллельность прямых. 10 класс.Скачать

7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

7 класс, 28 урок, Аксиома параллельных прямыхСкачать

7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

10 класс, 5 урок, Параллельность трех прямыхСкачать

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ 7 класс геометрия АтанасянСкачать

№58. Докажите, что если плоскость γ пересекает одну из параллельных плоскостей α и β,Скачать

Признаки параллельности прямых. Видеоурок по геометрии 7 классСкачать

Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать

Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Пересекающиеся и параллельные прямые, лучи, отрезки. Задачи. Геометрия. Математика 2 класс.Скачать