Если плоскость перпендикулярна одной из двух параллельных прямых то она (7 видео)

Геометрия. 10 класс

Содержание

Перпендикулярность прямых и плоскостей
Перпендикулярные прямые
Перпендикулярность прямой и плоскости
Признак перпендикулярности прямой и плоскости
Свойства перпендикулярных прямой и плоскости
Перпендикулярность плоскостей
Признак перпендикулярности плоскостей
Свойство перпендикулярных плоскостей
СВОЙСТВА ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ
💡 Видео

Конспект урока

Геометрия, 10 класс

Урок № 8 Перпендикулярность прямой и плоскости

Перечень вопросов, рассматриваемых по теме

Ввести понятие перпендикулярных прямых в пространстве;
Доказать лемму о перпендикулярности двух параллельных прямых;
Решать задачи по теме.

Глоссарий по теме

Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90. Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.

Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости

Теорема о прямой перпендикулярной к плоскости. Через любую точку пространства проходит плоскость, перпендикулярная к данной прямой.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл. Базовый и профильный уровень. М.: Просвещение, 2015. С.1-10.

Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 9 класса. Базовый и профильный уровень

Зив Б.Г. Геометрия. Дидактические материалы. 10-11 класс М.: Просвещение, 2015.

Открытые электронные ресурсы:

Перпендикулярность прямой и плоскости. http://school-collection.edu.ru // Единая коллекция цифровых образовательных ресурсов.

Перпендикулярность прямой и плоскости. https://www.yaklass.ru // Я-класс. Образовательный портал Сколково.

Теоретический материал для самостоятельного изучения

Через точку М пространства, не лежащую на данных прямых, проведем прямые МА и МС, параллельные соответственно прямым а и с. Так как а ⊥ с, то ∠АМС=90 о .

Итак, прямые b и с параллельны соответственно прямым МА и МС, угол между ними равен 90 о , т.е. b ‖ МА, с ‖ МС, угол между МА и МС равен 90 о

Это означает, что угол между прямыми b и с также равен 90 о , то есть b ⊥ с.

Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.

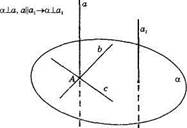
Проведем какую-нибудь прямую x в плоскости α, т.е. x ∊ α.Так как а ⊥ α, то а ⊥ x.

По лемме о перпендикулярности двух параллельных прямых к третьей а₁ ⊥ x.

Таким образом, прямая а₁ перпендикулярна к любой прямой, лежащей в плоскости α, т. е. а₁ ⊥ α

Теорема. Ели две прямые перпендикулярны плоскости, то они параллельны.

Через какую-нибудь точку М прямой b проведем прямую b₁, параллельную прямой а.

Докажем, что прямая b₁ совпадает с прямой b. Тем самым будем доказано, что а ‖ b. Допустим, что прямые b₁ и b не совпадают. Тогда в плоскости β, содержащей прямые b и b₁, через точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости α и β. Но это невозможно, следовательно, а ‖ b, т.е. b ∊ β, b₁ ∊ β, α β = c (невозможно)→ а ‖ b

Теорема. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Пусть дана плоскость α и точка М (см. рис. 2). Нужно доказать, что через точку М проходит единственная прямая с, перпендикулярная плоскости α.

Проведем прямую а в плоскости α (см. рис. 3). Согласно доказанному выше утверждению, через точку М можно провести плоскость γ перпендикулярную прямой а. Пусть прямая b – линия пересечения плоскостей α и γ.

В плоскости γ через точку М проведем прямую с, перпендикулярную прямой b.

Прямая с перпендикулярна b по построению, прямая с перпендикулярна а (так как прямая а перпендикулярна плоскости γ, а значит, и прямой с, лежащей в плоскости γ). Получаем, что прямая с перпендикулярна двум пересекающимся прямым из плоскости α. Значит, по признаку перпендикулярности прямой и плоскости, прямая с перпендикулярна плоскости α. Докажем, что такая прямая с единственная.

Предположим, что существует прямая с₁, проходящая через точку М и перпендикулярная плоскости α. Получаем, что прямые с и с₁ перпендикулярны плоскости α. Значит, прямые с и с₁ параллельны. Но по построению прямые с и с₁пересекаются в точке М. Получили противоречие. Значит, существует единственная прямая, проходящая через точку М и перпендикулярная плоскости α, что и требовалось доказать.

Теоретический материал для углубленного изучения

Доказательство (см. рис. 1)

Пусть нам дана прямая а и точка М. Докажем, что существует плоскость γ, которая проходит через точку М и которая перпендикулярна прямой а.

Через прямую а проведем плоскости α и β так, что точка М принадлежит плоскости α. Плоскости α и β пересекаются по прямой а. В плоскости α через точку М проведем перпендикуляр MN (или р) к прямой а, . В плоскости β из точки N восстановим перпендикуляр q к прямой а. Прямые р и q пересекаются, пусть через них проходит плоскость γ. Получаем, что прямая а перпендикулярна двум пересекающимся прямым р и q из плоскости γ. Значит, по признаку перпендикулярности прямой и плоскости, прямая а перпендикулярна плоскости γ.

Примеры и разборы решения заданий тренировочного модуля

Выбор элемента из выпадающего списка

Выпишите ребра, перпендикулярные плоскости (DC).

Правильный вариант/варианты (или правильные комбинации вариантов):

Неправильный вариант/варианты (или комбинации):

Подсказка: в кубе все углы по . Плоскость (DC), проходит через грань куба DC.

Разбор задания: Куб – это геометрическая фигура у которой все углы прямые, следовательно нужно увидеть ребра которые перпендикулярны к плоскости (DC), к грани куба (DDC).Эти ребра — AD, A₁D₁, BC, B₁C₁

Закончите предложение, чтобы получилось верное утверждение.

Две прямые называются перпендикулярными, если …..
Если плоскости перпендикулярна одной из двух параллельных прямых, то она ……

параллельны
один
она перпендикулярна к любой прямой, лежай в этой плоскости.
перпендикулярна плоскости.

Правильный вариант/варианты (или правильные комбинации вариантов):

Две прямые называются перпендикулярными, если …

угол между ними равен 90

Если плоскость перпендикулярна одной из двух параллельных прямых, то она …

перпендикулярна и другой

Неправильный вариант/варианты (или комбинации):

Лемма: Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к третьей прямой.

Теорема: если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

Видео:№132. Докажите, что если одна из двух параллельных плоскостей перпендикулярна к прямойСкачать

Перпендикулярность прямых и плоскостей

Видео:10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

Перпендикулярные прямые

Две прямые в пространстве называются перпендикулярными , если угол между ними составляет .

При этом прямые могут пересекаться,

а могут быть скрещивающимися:

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Перпендикулярность прямой и плоскости

Прямая называется перпендикулярной к плоскости , если она перпендикулярна любой прямой, лежащей в этой плоскости.

Признак перпендикулярности прямой и плоскости

Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Свойства перпендикулярных прямой и плоскости

1). Две прямые, перпендикулярные одной и той же плоскости, параллельны.

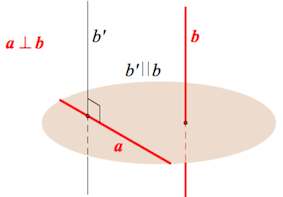
2). Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости.

3). Две плоскости, перпендикулярные одной и той же прямой, параллельны между собой

Видео:Параллельность прямых. 10 класс.Скачать

Перпендикулярность плоскостей

Пересекающиеся плоскости называются перпендикулярными , если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Признак перпендикулярности плоскостей

Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Свойство перпендикулярных плоскостей

Если прямая лежит в одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна второй плоскости.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

СВОЙСТВА ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ

Теорема 15. Если плоскость перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.

Доказательство. Пусть а || о₂ и а 1 ос . Докажем, что а_г L а (рис. 36). Так как а 1 а , то в плоскости а найдутся пересекающиеся в точке А прямые бис, перпендикулярные а (по определению). Так как Ьис перпендикулярны к прямой а, то по теореме 13 они перпендикулярны и к прямой a_v параллельной а. Поэтому по теореме 14 а_: ± а. Теорема доказана.

Рис. 36

Теорема 16(обратная теорема). Две прямые, перпендикулярные к одной плоскости, параллельны.

Доказательство. Пусть Докажем, что а \ Ь (рис. 37). Допустим, что прямые а и Ъ не параллельны. Выберем на прямой Ъ точку D, не лежащую в плоскости а. Проведем через точку D прямую b_v параллельную прямой а. Так как a L а, то и fc_x ± а (по теореме 15). Если Вт С — точки пересечения прямых Ъ и Ъ_г с плоскостью а, то из предположения следует, что в треугольнике BDC два прямых угла. Этого не может быть. Значит, прямые а и 6 параллельны. Теорема доказана.

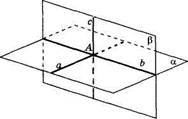Если плоскость перпендикулярна одной из двух параллельных прямых то она

Задача 2. Через точку А данной плоскости а провести перпендикулярную ей прямую.

Рис. 38

Решение. В плоскости а через точку А проведем прямую а (рис. 38). Через точку А проведем плоскость Д перпендикулярную к прямой а (задача 1). Пусть a n р = Ъ. В плоскости р через точку А проведем прямую с, перпендикулярную прямой Ь. Отсюда с L Ъ и с J. а. По признаку перпендикулярности прямой и плоскости (теорема 14) cL a. Итак, с — искомая прямая. Методом от противного можно доказать и единственность этой прямой.

Вопросы и задания

1. Докажите (теорему), что если плоскость перпен
дикулярна одной из двух параллельных прямых, то
она перпендикулярна и к другой.

2. Докажите (теорему), что две прямые, перпендику
лярные одной и той же плоскости, параллельны.

3. На рисунке 39 изображен прямоугольный парал
лелепипед. Используя рисунок, ответьте на вопросы:

1)К каким ребрам перпендикулярно основание ABCD?

2)Назовите пару ребер, перпендикулярных к грани ADDjA^.

4. В окружающей обстановке найдите примеры на свойства перпендикулярности прямой и плоскости.

Задачи

100.Сколько прямых, перпендикулярных к данной плоскости, можно
провести через данную точку? А отрезков?

101.а 1а. Как расположены относительно плоскости ос прямые, пер
пендикулярные к прямой а?

102.Постройте сечение куба плоскостью, проходящей через середину
его ребра перпендикулярно к этому ребру. Найдите площадь
сечения, если ребро куба равно 3 см.

103.Плоскость а перпендикулярна к катету МКпрямоугольного тре
угольника MNK и делит его в отношении |MMJ : M_tK = 3:2.
В каком отношении плоскость а делит гипотенузу MN?

104.Расстояния от точки Р до всех вершин квадрата равны, точка О —
центр квадрата. Докажите, что прямая РО перпендикулярна к
плоскости квадрата.

105.Постройте сечение правильного тетраэдра плоскостью, перпен
дикулярной к ребру и проходящей через середину этого ребра.
Найдите площадь сечения, если ребро тетраэдра равно 8 см.

106.Прямые АА₁ и BB_V перпендикулярные к плоскости а, пересекают
ее в точках А_х и B_lt а прямая АВ — в точке С. Найдите расстояние
AjBj, если [AAJ = 12 см, BB_t = 4 см, В£ = 2 см.

107.Треугольник ABC — равносторонний, а отрезок АО перпенди
кулярен к его плоскости. Найдите периметр и площадь треуголь
ника ОВС, если: 1) АВ = 6 см, АО = 8 см; 2) АВ = АО = о.

108. Прямые АА₁ и BB_V перпендикулярные к плоскости а, пересекают ее в точках А₁ и B_v а прямая АВ — в точке С. Найдите расстояние Bfi, если АА_Х = 12 см, IAjSJ = ВВ_г = 3 см.