Равные и подобные треугольники (3 видео)

Подобные треугольники

Содержание

Определение
Признаки подобия треугольников
Свойства подобных треугольников
Примеры наиболее часто встречающихся подобных треугольников
Признаки подобия и равенства треугольников. Свойства подобных треугольников
Какие треугольники называются подобными, а какие равными?
Признаки подобия
Прямоугольные треугольники: когда они подобны, а когда равны?
Свойства треугольников подобных
Пример решения задачи
Треугольники: признаки равенства и подобия треугольников, их основные элементы и замечательные точки
🎦 Видео

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Определение

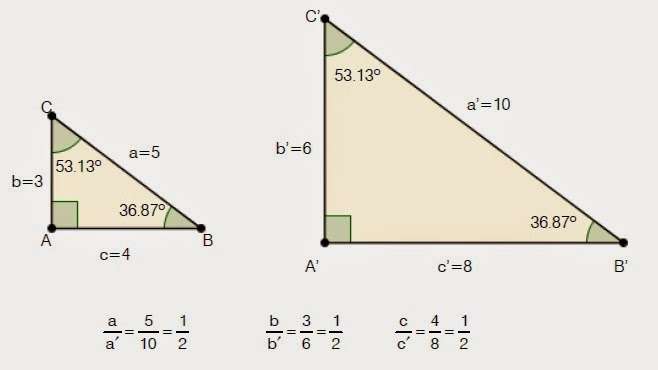
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.

Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.

Видео:8 класс, 21 урок, Отношение площадей подобных треугольниковСкачать

Признаки подобия треугольников

I признак подобия треугольников

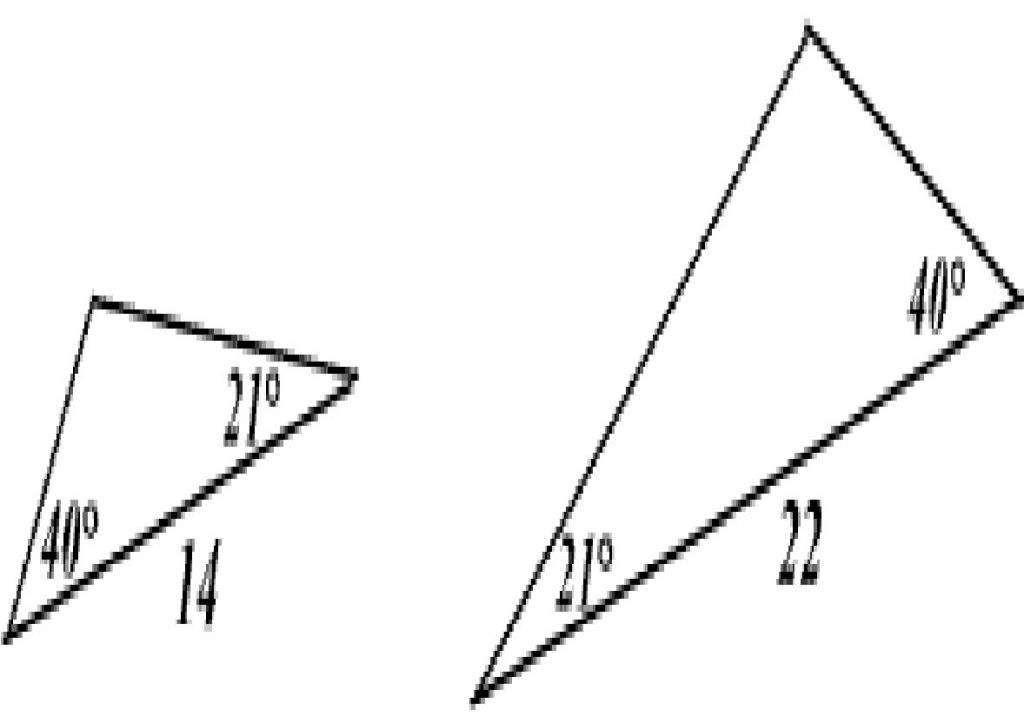
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Свойства подобных треугольников

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров подобных треугольников равно коэффициенту подобия.
Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.

Видео:Подобные треугольникиСкачать

Примеры наиболее часто встречающихся подобных треугольников

1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

Здесь вы найдете подборку задач по теме «Подобные треугольники» .

Видео:6 класс, 32 урок, Равные и подобные фигурыСкачать

Признаки подобия и равенства треугольников. Свойства подобных треугольников

Треугольник является самой простой замкнутой фигурой на плоскости. При изучении школьного курса геометрии рассмотрению его свойств уделяют особое внимание. В данной статье раскроем вопрос признаков подобия и равенства треугольников.

Видео:Признаки равенства треугольников. 7 класс.Скачать

Какие треугольники называются подобными, а какие равными?

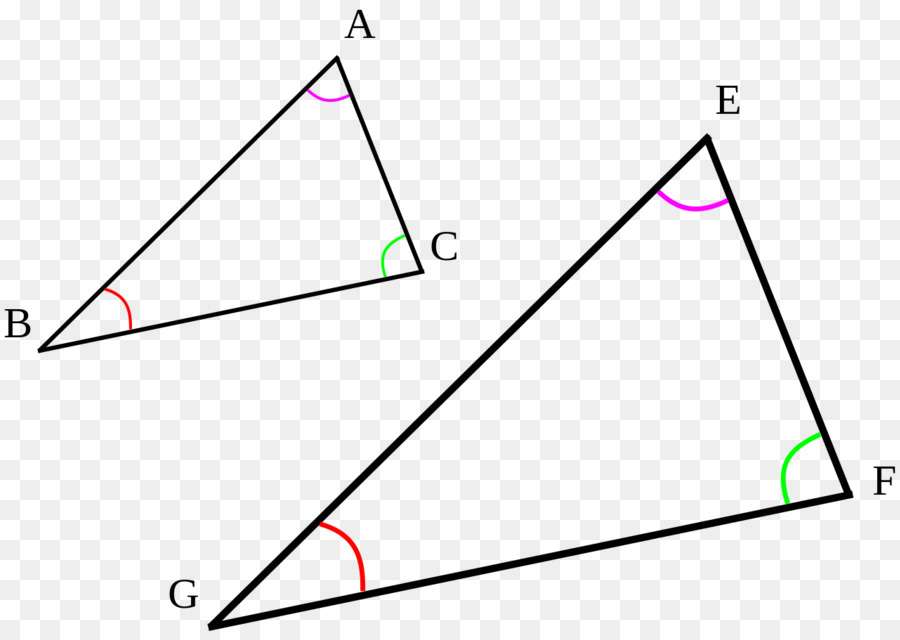
Логично предположить, что две рассматриваемые фигуры будут равны между собой, если они имеют все одинаковые углы и длины сторон. Что касается подобия, то здесь дело обстоит немного сложнее. Два треугольника будут подобны тогда, когда каждый угол одного будет равен соответствующему углу другого, а стороны, лежащие напротив равных углов обеих фигур, будут пропорциональны. Ниже изображен рисунок, на котором представлены два подобных треугольника.

Вам будет интересно: Полемизировать – это значит, спорить правильно

Используя этот рисунок, запишем в виде математических равенств данное выше определение: B = G, A = E, C = F, BA / GE = AC / EF = BC / GF = r, здесь одна латинская буква означает угол, а две буквы — длину стороны. Величина r носит название коэффициента подобия. Понятно, что если r = 1, то имеют место не только подобные, но и равные треугольники.

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Признаки подобия

Говоря о свойствах и признаках подобия и равенства треугольников, следует перечислить три основных критерия, по которым можно определить, являются ли рассматриваемые фигуры подобными или нет.

Итак, две фигуры будут подобными между собой, если выполняется одно из следующих условий:

Их два угла равны. Поскольку сумма углов треугольника эквивалентна 180o, то равенство первых двух из них автоматически означает, что одинаковыми будут и третьи. Используя рисунок выше, этот признак можно записать так: если B = G и A = E, то ABC и GEF являются подобными. Если же в этом случае будут равными хотя бы по одной стороне обоих фигур, тогда можно говорить о полной эквивалентности треугольников.

Две стороны пропорциональны и углы между ними одинаковые. Например, BA / GE = AC / EF и A = E, тогда GEF и ABC будут подобными. Заметим, что углы A и E лежат между соответствующими пропорциональными сторонами.

Все три стороны взаимно пропорциональны. Излагая математическим языком, получаем: BA / GE = AC / EF = BC / GF = r, тогда рассматриваемые фигуры тоже являются подобными.

Отметим еще раз, что для доказательства подобия достаточно привести какой-либо один из представленных признаков. Логично, что все остальные будут выполняться также.

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Прямоугольные треугольники: когда они подобны, а когда равны?

Говоря о признаках равенства и подобия прямоугольных треугольников, следует отметить сразу, что у каждого из них по одному углу уже равны (90o).

Последний факт приводит к следующей формулировке изложенных выше критериев подобия:

Если в двух треугольниках прямоугольных равен всего один угол, который не является прямым, то такие фигуры подобны между собой.

Если катеты пропорциональны между собой, тогда фигуры тоже будут подобны, поскольку угол между катетами является прямым.

Наконец, пропорциональности всего двух любых сторон для обоих прямоугольных треугольников достаточно для доказательства их подобия. Причина этого заключается в том, что стороны данных фигур связаны между собой теоремой Пифагора, поэтому пропорциональность 2-х из них приводит к пропорциональности с аналогичным коэффициентом подобия и для третьих сторон.

Что касается равенства треугольников с прямыми углами, то здесь просто запомнить: если два каких-либо элемента (прямой угол не считается) обеих фигур равны, то равны и сами фигуры. Например, этими двумя элементами могут быть острый угол и катет, катет и гипотенуза или гипотенуза и острый угол.

Видео:Треугольники. 7 класс.Скачать

Свойства треугольников подобных

Из рассмотренных признаков подобия и равенства треугольников свойства можно выделить такие:

Периметры этих фигур относятся друг к другу как коэффициент подобия, то есть P1 / P2 = r, где P1 и P2 — периметры 1-го и 2-го треугольников, соответственно.

Площади подобных фигур относятся как квадрат коэффициента подобия, то есть: S1 / S2 = r2, где S1 и S2 — площади 1-го и 2-го треугольников, соответственно.

Оба эти свойства можно доказать самостоятельно. Суть доказательства сводится к применению математической записи подобия между сторонами фигур. Здесь приведем лишь доказательство 1-го свойства.

Пусть a, b, c — длины сторон одного треугольника и a’, b’, c’ — стороны второго. Поскольку фигуры подобны, то можно записать: a = r * a’, b = r * b’, c = r * c’. Теперь эти выражения подставим в отношении их периметров, получим: P1 / P2 = (a + b + c) / (a’ + b’ + c’) = (r * a’ + r * b’ + r*c’) / (a’ + b’ + c’) = r(a’ + b’ + c’) / (a’ + b’ + c’) = r.

Видео:ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать

Пример решения задачи

Признаки подобия и равенства треугольников можно использовать для решения различных геометрических задач. Ниже приводится один из примеров.

Имеются два треугольника. У одного из них стороны равны 7,6 см, 4,18 см и 6,65 см, а у другого 3,5 см, 2,2 см и 4 см. Необходимо определить, подобны ли эти фигуры.

Поскольку даны значения трех сторон, то можно сразу проверить 3-й критерий подобия. Сложность здесь состоит в том, что нужно понять, между какими сторонами брать отношения. Тут следует воспользоваться простыми логическими рассуждениями: коэффициенты подобия могут быть равными, если делить самую маленькую сторону одного треугольника на аналогичную для другого и так далее. Поэтому имеем: 4,18 / 2,2 = 1,9; 6,65 / 3,5 = 1,9; 7,6 / 4 = 1,9. Проверив отношение всех сторон, можно с уверенностью сказать, что треугольники являются подобными, поскольку выполняется 3-й критерий.

Видео:Равенство Vs подобие треугольников. Вебинар | TutorOnlineСкачать

Треугольники: признаки равенства и подобия треугольников, их основные элементы и замечательные точки

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Тема этого урока – «Треугольники: признаки равенства и подобия треугольников, их основные элементы и замечательные точки». На нем мы повторим знания, полученные нами еще в 7 классе в рамках курса планиметрии, рассмотрим центральную фигуру всей геометрии – треугольник. Дадим определение признакам равенства и подобия треугольников, изучим еще раз их основные элементы и назовем замечательные точки.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»