Взаимное положение прямых в пространстве

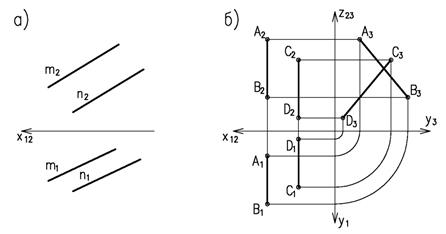
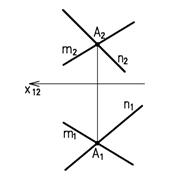
Две прямые в пространстве могут быть параллельными, пересекающимися или скрещивающимися. Если две прямые параллельны, то их одноименные проекции взаимно параллельны (рис. 4.8). Если две прямые пересекаются, то точки пересечения одноименных проекций принадлежат одной линии связи (рис. 4.9). В частном случае пересекающиеся прямые могут быть перпендикулярными.

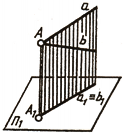
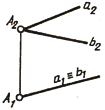
a b ; плоскость П`, b||П`

Доказать, что a’ b’.

Для доказательства через прямые а’ и а вводится дополнительная плоскость . Прямая b перпендикулярна к плоскости и параллельна проекции прямой b’. Отсюда прямая V тоже перпендикулярна к плоскости .

Прямая а’ принадлежит плоскости , следовательно, а’ перпендикулярна к b’, т.е. прямой угол проецируется без искажения.

Если две прямые не параллельны и не пересекаются, т.е. не лежат в одной плоскости, то они являются скрещивающимися (рис. 4.11).

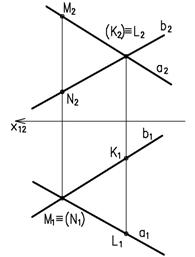
Взаимное положение двух прямых при наличии профильной прямой устанавливается по третьей проекции или каким-либо иным способом. На рис. 4.12 изображены две скрещивающиеся прямые, хотя их горизонтальные и фронтальные проекции пересекаются, а профильные — параллельны между собой.

Глава 7. Изображение линий на чертежах

Глава 7Образование линийКомплексные чертежи прямых линийРасположение прямой относительно плоскостей проекцийВзаимное расположение двух прямыхОпределение натуральной величины отрезка прямой линииКривые линииВзаимное расположение точки и линииВопросы

§ 41. Взаимное расположение двух прямых

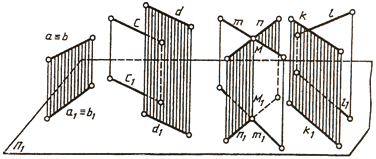
Две прямые пространства могут иметь различное расположение (рис. 74). Они могут совпадать а ≡ b, быть параллельными с ׀׀ d, пересекаться m ∩ n и скрещиваться (k°/l).

Если две прямые параллельны, то на комплексном чертеже (рис. 75, а) их одноименные проекции параллельны.

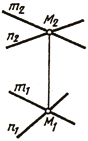
Если две прямые пересекаются в некоторой точке М, то проекции этой точки должны принадлежать одноименным проекциям прямых, т. е. точки пересечения одноименных проекций пересекающихся прямых должны лежать на одной линии связи (рис. 75, б):

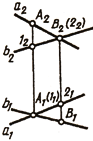
Если две прямые скрещиваются, то их одноименные проекции могут пересекаться в точках, не лежащих на одной линии связи (рис. 75, в):

A₁ (1₁) — горизонтально конкурирующие точки;

B₂ (2₂) — фронтально конкурирующие точки.

В другом случае одна пара проекций будет пересекаться, а вторая может быть параллельными прямыми (рис. 75, г):

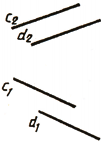
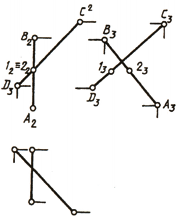
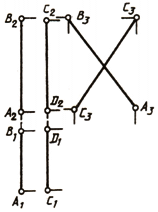
Следует обратить внимание на особые случаи определения взаимного расположения двух прямых в пространстве. Если одна из них (рис. 76, а) или обе (рис. 76, 6) окажутся профильными прямыми, то для определения взаимного расположения их необходимо построить третью, профильную проекцию этих прямых.

Если рассматривать рис. 76, а, можно ошибочно сделать предположение, что прямые АВ и CD пересекаются. Однако если построить профильные проекции этих прямых, станет видно, что они скрещиваются, так как точки 1 и 2 не совпадают, а являются фронтально конкурирующими точками.

Рассматривая рис. 76, б,можно ошибочно предположить, что прямые АВ и CD параллельны. Но после построения их профильных проекций увидим, что они скрещиваются, так как на этой плоскости проекции их пересекаются.

Две прямые, параллельные или пересекающиеся, могут иметь общую проецирующую плоскость (рис. 77, а).Тогда их изображения на соответствующую плоскость проекций совпадут. Такие прямые называют конкурирующими .

Прямые а и b горизонтально конкурирующие, имеют общую горизонтально проецирующую плоскость (рис. 77, б).

Прямые с и d (рис. 77, в) — фронтально конкурирующие, имеют общую фронтально проецирующую плоскость.

© Красноярский государственный аграрный университет
© Управление информационных технологий
© Кафедра Технологии машиностроения

Взаимное положение двух прямых.

Две прямые линии в пространстве могут бытьпараллельными, пересекающимися и скрещивающимися. Их положение в пространстве устанавливается взаимным расположением одноименных проекций.

Если в пространстве две прямые параллельны, то их одноименные проекции также параллельны (рисунок 1.11а).

Параллельность профильных прямых не всегда очевидна. Хотя их горизонтальные и фронтальные проекции параллельны, сами прямые могут быть не параллельны. Для определения их взаимного положения можно построить профильную проекцию (рисунок 1.11б).

Пересекающиеся прямые – это прямые, имеющие общую точку, следовательно, если прямые в пространстве пересекаются, то точки пересечения их одноименных проекций лежат на одной линии проекционной связи (рисунок 1.12).

Скрещивающиеся прямыене имеют общей точки, поэтому точки пересечения их одноименных проекций не лежат на одной линии проекционной связи (рисунок 1.13).

Пары точек, у которых какие-либо одноименные проекции совпали, т.е. они лежат на одном проецирующем луче, называютсяконкурирующими (одна из них «закрывает» другую). Точки M и N – горизонтально-конкурирующие, точки K и L – фронтально-конкурирующие. Из двух конкурирующих точек видна та, у которой больше одна из координат (две другие совпадают).

Например, координата Z у точки М больше, чем у точки N , следовательно, прямая а в этом месте расположена выше прямой в и будет видима при взгляде сверху, т.е. на горизонтальной проекции. Аналогично, у точки L координата Y больше, чем у точки К, следовательно, в этом месте прямая а расположена ближе к зрителю и будет видима на фронтальной проекции. Определение видимости конкурирующих точек позволит нам в дальнейшем определять видимость прямой относительно плоскости.

Дата добавления: 2015-09-18 ; просмотров: 1181 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ