Чертежик

Содержание

Метки
Взаимное расположение прямых линий
Проекции параллельных прямых
Глава 7. Изображение линий на чертежах
§ 41. Взаимное расположение двух прямых
📸 Видео

Метки

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Взаимное расположение прямых линий

Взаимное расположение прямых линий может быть представлено следующим образом: быть параллельными, пересекаться, скрещиваться.

1. Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.

Проекции параллельных прямых на любую плоскость проекций (не перпендикулярную данным прямым) — параллельны.

Пересекающимисяназываются две прямые лежащие в одной плоскости и имеющие одну общую точку.

Прямые пересекаются, если их одноименные проекции также пересекаются, а проекции точки пересечения лежат на одной линии связи.

Скрещивающимисяназываются две прямые не лежащие в одной плоскости.

Прямые скрещиваются, если они не пересекаются и не параллельны между собой, а точки пересечения их одноименных проекций не лежат на одной линии связи.

Примеры выполненных чертежей смотрите в этом разделе .

Видео:Параллельность прямых. 10 класс.Скачать

Проекции параллельных прямых

Если прямые в пространстве параллельны, то их проекции также параллельны (рис. 5). Доказательство: прямые АВ и CD проецируются с помощью проецирующих плоскостей У и Т, но У¦Т, т. к. АВ¦CD по условию и ААN¦ССN — по построению. Известно, что если две параллельные плоскости пересекаются третьей, то образуются параллельные прямые. Здесь две параллельные плоскости У и Т пересекаются плоскостью проекций ПN и образуются параллельные прямые (АNВN¦CNDN).

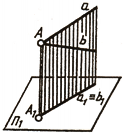
Проекции геометрических фигур, параллельных плоскости проекций. Если данная геометрическая фигура — прямая, кривая линия или плоская фигура (треугольник, многоугольник, эллипс, окружность и т. п.) лежит в плоскости, параллельной плоскости проекций, то она проецируется на плоскость проекций в натуральную величину. Доказательство: дано У¦ПN и АВ У (рис. 6). Требуется доказать, что АВ¦АNВN и АВ=АNВN. Так как У¦ПN , то отрезки ААN и ВВN равны и параллельны. Следовательно, четырехугольник АВВNАN является параллелограммом и АВ¦АNВN, АВ=АNВN.

Так же доказывается теорема относительно любой плоской кривой и любой плоской фигуры.

— цилиндрические поверхности в параллельной системе проецирования и конические поверхности в центральной системе проецирования — проецируют пространственные кривые линии и пространственные фигуры.

Основное свойство проецирующей геометрической фигуры заключается в том, что точки, прямые или кривые линии, плоские и пространственные фигуры, расположенные на проецирующей геометрической фигуре, проецируются на линию пересечения этой фигуры с плоскостью проекций. Эта линия называется следом данной проецирующей геометрической фигуры или ее главной проекцией.

На рис. 7 показаны проецирующие геометрические фигуры в ортогональной системе проецирования: проецирующая прямая а, проецирующая плоскость У и проецирующая цилиндрическая поверхность Ф.

Прямая а, плоскость У и образующие цилиндрической поверхности Ф перпендикулярны плоскости проекций ПN . Их главные проекции аN , УN и ФN включают в себя проекции всех точек данной проецирующей геометрической фигуры.

Дополнения однокартинного чертежа. Ранее было показано, что одна проекция точки не определяет ее положения в пространстве.

Для того, чтобы чертеж был полным и обратимым, т.е. для того, чтобы по чертежу можно было представить положение точки в пространстве, применяются разные способы.

Способ числовых отметок. Около проекции точки ставится число, выражающее в некоторых линейных единицах расстояние данной точки от плоскости проекций.

На рис. 8 даны проекции различных геометрических фигур с числовыми отметками.

Около проекции точки А стоит цифра 20. Это означает, что точка А отстоит от плоскости проекций на расстоянии 20 линейных единиц.

Концы отрезка ВС отстоят от плоскости на расстояниях 15 и 30, вершины треугольника DEF — на расстояниях соответственно 0, 10 и 25.

Кривая поверхность задана кривыми линиями, принадлежащими поверхности и параллельными плоскости проекций (горизонталями, если плоскость ПN горизонтальна). Около каждой горизонтали стоит число, выражающее ее расстояние от плоскости ПN.

С помощью горизонталей изображается рельеф земной поверхности на топографических картах и сложные кривые поверхности, в том числе поверхности манекена и обувной колодки.

Проекции, полученные при центральном и параллельном проецировании, обладают рядом свойств.

Проекция точки есть точка. При заданном центре Р (.или направлении S) проецированию любой точки А пространства соответствует иа плоскости проекций п’ единственная точка А’. При этом проекция точки В, лежащей в плоскости проекций, совпадает с самой точкой (см. рис. 43).

Проекция прямой есть прямая. На рис. 46 лучи, проецирующие прямую т, создают плоскость S, которая пересекает плоскость проекций п’ по линии m’, являющейся проекцией на плоскость n’; S

т; S п п = т’. Проекция прямой определена, если известны проекции хотя бы двух ее точек (рис. 9). Если в пространстве прямая параллельна плоскости проекции п’, то ее проекция параллельна самой прямой (рис. 10). При этом при центральном проецировании проекции отрезков пропорциональны самим отрезкам, а при параллельном — равны им.

При параллельном проецировании сохраняется отношение величин отрезков прямой и их проекций (рис. 11):

При параллельном проецировании проекции параллельных прямых есть прямые параллельные (рис. 12). Если прямые т и п в пространстве параллельны, то и проецирующие их плоскости Sm и Sn тоже будут параллельны. При пересечении их с плоскостью проекций п’ получаем т’|| п’.

Проекцией плоскости является плоскость проекций. Плоскость состоит из бесконечного множества точек. При проецировании этого множества проецирующие лучи заполняют все пространство, а их точки пересечения с плоскостью проекций п’ — всю плоскость проекций.

Так как положение любой плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой, то проекция трех таких точек плоскости (рис. 13, а) устанавливает однозначное соответствие между проецирующей плоскостью и плоскостью проекций n’, которое позволяет определить проекции (рис. 13, б) любой точки D или прямой этой плоскости.

Если плоскость параллельна плоскости проекций, то проекции ее плоских фигур при центральном проецировании подобны самим фигурам (рис. 14, а), а при параллельном — равны им (рис. 14,6).

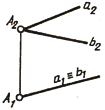
Если плоскость угла параллельна плоскости проекций, величина проекции угла и при центральном, и при параллельном проецировании равна натуральной величине. На рис. 54, a угол ABC = уголA’B’C’, так как АВС бесконечность А’В’С’, а на рис. 54, б угол ABC = углу А’В’С’, так как АВС = А’В’С’.

При параллельном проецировании проекции фигуры не изменяется при параллельном переносе плоскости j проекций (рис. 15).

Прямые и плоскости (поверхности) могут занимать в пространстве проецирующее положение, если с ними совпадают проецирующие лучи. При центральном проецировании это прямые и плоскости, проходящие через центр проекций, пирамидальные и конические поверхности, у которых вершины совпадают с центром проецирования (рис. 56). При параллельном проецировании — это прямые и плоскости, параллельные направлению проецирования, призматические и цилиндрические поверхности, ребра и образующие которых параллельны направлению проецирования (рис. 57).

Все эти геометрические фигуры можно рассматривать состоящими из проецирующих лучей, каждый из которых изображается точкой. Отсюда следует, что проекциями прямых, плоскостей, поверхностей, занимающих проецирующее положение, есть точки или линии их пересечения с плоскостью проекций («вырожденные» проекции).

Глава 7. Изображение линий на чертежах

Глава 7Образование линийКомплексные чертежи прямых линийРасположение прямой относительно плоскостей проекцийВзаимное расположение двух прямыхОпределение натуральной величины отрезка прямой линииКривые линииВзаимное расположение точки и линииВопросы

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

§ 41. Взаимное расположение двух прямых

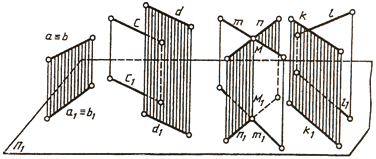
Две прямые пространства могут иметь различное расположение (рис. 74). Они могут совпадать а ≡ b, быть параллельными с ׀׀ d, пересекаться m ∩ n и скрещиваться (k°/l).

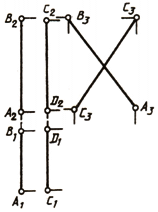
Если две прямые параллельны, то на комплексном чертеже (рис. 75, а) их одноименные проекции параллельны.

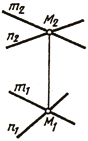
Если две прямые пересекаются в некоторой точке М, то проекции этой точки должны принадлежать одноименным проекциям прямых, т. е. точки пересечения одноименных проекций пересекающихся прямых должны лежать на одной линии связи (рис. 75, б):

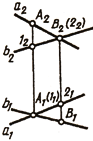
Если две прямые скрещиваются, то их одноименные проекции могут пересекаться в точках, не лежащих на одной линии связи (рис. 75, в):

A₁ (1₁) — горизонтально конкурирующие точки;

B₂ (2₂) — фронтально конкурирующие точки.

В другом случае одна пара проекций будет пересекаться, а вторая может быть параллельными прямыми (рис. 75, г):

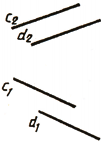
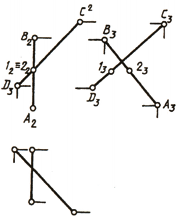
Следует обратить внимание на особые случаи определения взаимного расположения двух прямых в пространстве. Если одна из них (рис. 76, а) или обе (рис. 76, 6) окажутся профильными прямыми, то для определения взаимного расположения их необходимо построить третью, профильную проекцию этих прямых.

Если рассматривать рис. 76, а, можно ошибочно сделать предположение, что прямые АВ и CD пересекаются. Однако если построить профильные проекции этих прямых, станет видно, что они скрещиваются, так как точки 1 и 2 не совпадают, а являются фронтально конкурирующими точками.

Рассматривая рис. 76, б,можно ошибочно предположить, что прямые АВ и CD параллельны. Но после построения их профильных проекций увидим, что они скрещиваются, так как на этой плоскости проекции их пересекаются.

Две прямые, параллельные или пересекающиеся, могут иметь общую проецирующую плоскость (рис. 77, а).Тогда их изображения на соответствующую плоскость проекций совпадут. Такие прямые называют конкурирующими .