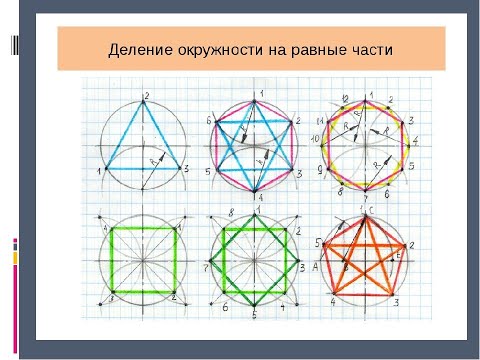
Как разделить окружность на 24 равных частей

Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.

Термины при построениях окружности

Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.

Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.

Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.

Части окружностей называются дугами.

Прямая СD, соединяющая две точки на окружности, называется хордой.

Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.

Часть круга, ограниченная хордой СD и дугой, называется сигментом.

Часть круга, ограниченная двумя радиусами и дугой, называется сектором.

Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.

Угол, образованный двумя радиусами КОА, называется центральным углом.

Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.

Видео:Деление круга на части без транспортираСкачать

Деление окружности на 4 и 8 одинаковых частей

Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.

Видео:Divide a Circle into 24 equal part using only a compassСкачать

Деление окружности на 3 и 6 равных частей (кратные 3 трём)

Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.

Видео:Деление окружности на n- равные частиСкачать

Деление окружности на 5 и 10 равных частей

Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки «а» в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке «b». Радиусом R3 из точки «1» проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние «b-О» даёт сторону правильного десятиугольника.

Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)

Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки «1» окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.

Видео:деление окружности на произвольное число частейСкачать

Нахождение центра дуги окружности

Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.

Видео:Деление окружности на равные части с помощью циркуляСкачать

Деление круга на равные части

Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами

Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала — традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним — нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.

Деление круга на равные по площади части радиусами

Деление круга на равные по площади части параллельными хордами

Деление круга на равные части радиусами

Традиционный и очень простой метод деления круга — по факту, нарезка равных секторов. Метод и формулы очень просты:

1. Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.

1. Определяем размер дуги сектора, перемножая радиус на угол в радианах

1. Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.

Собственно и всё — мы получили все характеристики для N равных секторов

Деление круга на равные части параллельными хордами

Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.

Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.

Верхнюю полуокружность можно представить графиком функции y=f(x), где x — это координата вдоль оси абсцисс, а y — это функция, численно равная y координате соответствующей точки верхней полуокружности.

По теореме Пифагора получаем следующую функцию

Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:

Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем

Итак, полное выражение

Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)

Таким образом мы можем приравнять

Что дает нам такое финальное уравнение

Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона.

Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее.

Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.

Видео:Деление окружности на 12 равных частейСкачать

Как поделить окружность на 24

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Деление окружности на любое число равных частей

Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.

Термины при построениях окружности

Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.

Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.

Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.

Части окружностей называются дугами.

Прямая СD, соединяющая две точки на окружности, называется хордой.

Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.

Часть круга, ограниченная хордой СD и дугой, называется сигментом.

Часть круга, ограниченная двумя радиусами и дугой, называется сектором.

Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.

Угол, образованный двумя радиусами КОА, называется центральным углом.

Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.

Видео:КАК РАЗДЕЛИТЬ ОКРУЖНОСТЬ НА 12 РАВНЫХ ЧАСТЕЙ?Скачать

Деление окружности на 4 и 8 одинаковых частей

Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.

Видео:Как разделить круг на равные частиСкачать

Деление окружности на 3 и 6 равных частей (кратные 3 трём)

Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.

Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Деление окружности на 5 и 10 равных частей

Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки «а» в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке «b». Радиусом R3 из точки «1» проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние «b-О» даёт сторону правильного десятиугольника.

Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)

Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки «1» окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.

Видео:Построение шестнадцатиугольника циркулемСкачать

Нахождение центра дуги окружности

Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.

Видео:Красивое деление окружности на 20 частей циркулемСкачать

Деление круга на равные части

Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами

Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала — традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним — нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.

Деление круга на равные по площади части радиусами

Деление круга на равные по площади части параллельными хордами

Деление круга на равные части радиусами

Традиционный и очень простой метод деления круга — по факту, нарезка равных секторов. Метод и формулы очень просты:

1. Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.

1. Определяем размер дуги сектора, перемножая радиус на угол в радианах

1. Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.

Собственно и всё — мы получили все характеристики для N равных секторов

Деление круга на равные части параллельными хордами

Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.

Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.

Верхнюю полуокружность можно представить графиком функции y=f(x), где x — это координата вдоль оси абсцисс, а y — это функция, численно равная y координате соответствующей точки верхней полуокружности.

По теореме Пифагора получаем следующую функцию

Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:

Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем

Итак, полное выражение

Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)

Таким образом мы можем приравнять

Что дает нам такое финальное уравнение

Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона.

Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее.

Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.

Видео:Деление окружности на N равных частей. Урок 8. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Деление окружности на любое число равных частей

Умение делить окружность на равные части необходимо для построения правильных многоугольников. Рассмотрим сначала частные приёмы деления окружности.

Деление на три части (рис. 15).

Ставим ножку циркуля в один из концов взаимно перпендикулярных диаметров окружности. Раствором циркуля, равным радиусу окружности, делаем засечки на ней по обе стороны от этого конца диаметра. Получаем две вершины правильного треугольника. Третьей вершиной является противоположный конец диаметра.

Деление на четыре части (рис. 16).

Два взаимно перпендикулярных диаметра делят окружность на четыре равные части. Если через центр окружности провести прямые под углом 45° к осям, то они также разделят окружность на четыре равные части. Стороны вписанного квадрата будут параллельны осям окружности. Вместе эти два квадрата разделили окружность на восемь равных частей.

Деление на пять частей (рис. 17).

• • Ставим ножку циркуля в один из концов диаметра (точка 7). Раствором циркуля, равным радиусу, делаем засечку на окружности. Получаем точку 2.
• • Из точки 2 опускаем перпендикуляр на тот диаметр, из конца которого была сделана засечка. Получаем точку 3.
• • Ставим ножку циркуля в точку 3. Берём радиус, равный расстоянию от точки 3 до конца вертикального диаметра (точка 4) и проводим дугу до пересечения с горизонтальным диаметром. Получаем точку 5.
• • Соединяем точки 4 и 5. Хорда 4

5 будет составлять 1/5 часть окружности.

Деление на шесть частей (рис. 18).

Раствором циркуля, равным радиусу окружности, делаем засечки из обоих концов одного и того же диаметра в обе стороны от них. Получаем четыре вершины правильного шестиугольника. Двумя другими вершинами являются концы диаметра, из которых сделаны засечки.

Деление на семь частей (рис. 19).

• • Ставим ножку циркуля в один из концов диаметра (точка 7). Раствором циркуля, равным радиусу окружности, делаем на ней засечку. Получаем точку 2.
• • Из точки 2 опускаем перпендикуляр на тот диаметр, из конца которого была сделана засечка. Получаем точку 3. Отрезок 2-3 составляет 1/7 часть окружности.
• • Замеряем циркулем длину отрезка 2-3 и последовательно откладываем его от любого конца диаметра сразу с двух сторон. Последний отрезок должен быть перпендикулярен диаметру, от конца которого начали откладывать отрезки. Этот диаметр будет осью симметрии вписанного семиугольника.

Деление на десять частей (рис. 20).

• • Делим окружность на 5 частей, как показано на рис. 17. Получаем правильный пятиугольник.
• • Из каждой вершины пятиугольника опускаем перпендикуляры на противолежащие стороны. Все они пройдут через центр окружности и разделят сторону и стягивающую её дугу пополам. Получим ещё 5 вершин.

Деление на двенадцать частей (рис. 21).

Раствором циркуля, равным радиусу окружности, делаем засечки из концов обоих диаметров по обе стороны от них.

Деление на четырнадцать частей (рис. 22).

• • Делим окружность на 7 частей, как показано на рис. 19. Получаем правильный семиугольник.
• • Через каждую вершину семиугольника и центр окружности проводим диаметры. Они разделят противолежащие стороны и стягивающие их дуги пополам. Получим ещё 7 вершин.

Существует и общий приём деления окружности на любое число частей. Рассмотрим его на примере построения правильного девятиугольника (рис. 23).

• • Проводим два взаимно перпендикулярных диаметра (горизонтальный и вертикальный).
• • Тот диаметр, который хотим сделать осью симметрии фигуры, делим на столько частей, на сколько требуется разделить окружность. На рис. 23 диаметр АВ разделён на 9 частей. Полученные точки деления нумеруем.
• • Ставим ножку циркуля в точку А и радиусом, равным диаметру окружности проводим дугу до пересечения с продолжением вертикального диаметра. Получаем точку С.
• • Точку С соединяем через одну с точками деления диаметра и продолжаем до пересечения с противолежащей дугой окружности в точках /, //, III, IV. Если одной из вершин девятиугольника должна быть точка А, то лучи проводим через все чётные деления диаметра (рис. 23, а). Если же одной из вершин должна стать точка В, то лучи следует проводить через все нечётные деления диаметра (рис. 23, б).
• • Симметрично отображаем построенные точки относительно горизонтального диаметра. Получаем остальные вершины фигуры.

Деление окружности на равные части можно использовать при создании различных форм орнаментов и розеток (рис. 24).

💥 Видео

Построение 12 угольника циркулемСкачать

Как разделить окружность на равные части.Скачать

Построение 10 угольника циркулемСкачать

Деление окружностиСкачать

Как разделить окружность на равные части!Скачать

Построение пятиугольника циркулемСкачать

1 2 3 деление окружности на 7 равных частейСкачать