В геометрии для изучения фигур используют две важные характеристики: длины сторон и углы между ними. В случае пространственных фигур к этим характеристиками добавляются двугранные углы. Рассмотрим, что это такое, а также опишем методику определения этих углов на примере пирамиды.
Видео:Определение истинной величины двугранного угла АВСD при ребре АВ методом замены плоскостей проекцииСкачать
Понятие о двугранном угле
Каждый знает, что две пересекающиеся прямые образуют некоторый угол с вершиной в точке их пересечения. Этот угол можно измерить с помощью транспортира или воспользоваться тригонометрическими функциями для его вычисления. Образованный двумя прямыми угол называется линейным.
Вам будет интересно: Географическая справка: площадь России в кв. км
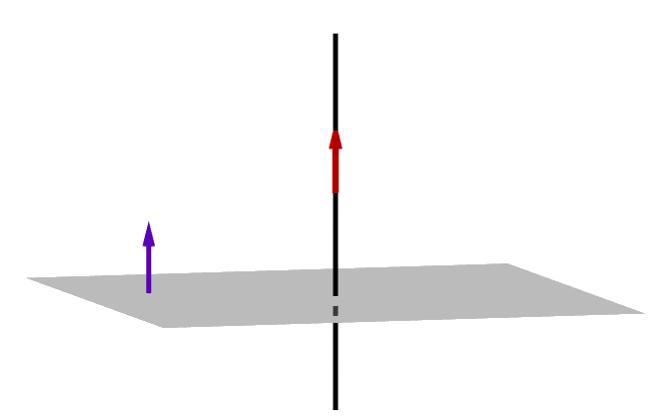
Теперь представим, что в трехмерном пространстве имеется две плоскости, которые пересекаются по прямой. Они изображена на рисунке.
Двугранным углом называется угол между двумя пересекающимися плоскостями. Так же как и линейный, он измеряется в градусах или радианах. Если к какой-либо точке прямой, по которой плоскости пересекаются, восстановить два перпендикуляра, лежащих в этих плоскостях, то угол между ними будет искомым двугранным. Определить этот угол проще всего, если воспользоваться уравнениями плоскостей в общем виде.
Видео:№174. Найдите двугранный угол ABCD тетраэдра ABCD, если углы DAB, DAC и ACB прямые, ACСкачать
Уравнение плоскостей и формула для угла между ними
Уравнение любой плоскости в пространстве в общем виде записывается так:
A × x + B × y + C × z + D = 0.
Здесь x, y, z — это координаты точек, принадлежащих плоскости, коэффициенты A, B, C, D — некоторые известные числа. Удобство этого равенства для вычисления двугранных углов заключается в том, что оно в явном виде содержит координаты направляющего вектора плоскости. Будем обозначать его n¯. Тогда:
Вектор n¯ перпендикулярен плоскости. Угол между двумя плоскостями равен углу между их направляющими векторами n1¯ и n2¯. Из математики известно, что угол, образованный двумя векторами, однозначно определяется из их скалярного произведения. Это позволяет записать формулу для вычисления двугранного угла между двумя плоскостями:
φ = arccos (|(n1¯ × n2¯)| / (|n1¯| × |n2¯|)).
Если подставить координаты векторов, то формула запишется в явном виде:
φ = arccos (|A1 × A2 + B1 × B2 + C1 × C2| / (√(A12 + B12 + C12) × √(A22 + B22 + C22))).
Знак модуля в числителе используется, чтобы определить только острый угол, поскольку двугранный угол всегда меньше или равен 90o.
Видео:10 класс, 22 урок, Двугранный уголСкачать
Пирамида и ее углы
Пирамидой называют фигуру, которая образована одним n-угольником и n треугольниками. Здесь n — целое число, равное количеству сторон многоугольника, который является основанием пирамиды. Данная пространственная фигура является многогранником или полиэдром, поскольку она состоит из плоских граней (сторон).
Двугранные углы многогранника-пирамиды могут быть двух типов:
- между основанием и боковой стороной (треугольником);
- между двумя боковыми сторонами.
Если рассматривается пирамида правильная, то названные углы для нее определить несложно. Для этого по координатам трех известных точек следует составить уравнение плоскостей, а затем воспользоваться приведенной в пункте выше формулой для угла φ.
Ниже приведем пример, в котором покажем, как найти двугранные углы при основании пирамиды четырехугольной правильной.
Видео:10 класс - Геометрия - Двугранный уголСкачать
Четырехугольная правильная пирамида и угол при ее основании
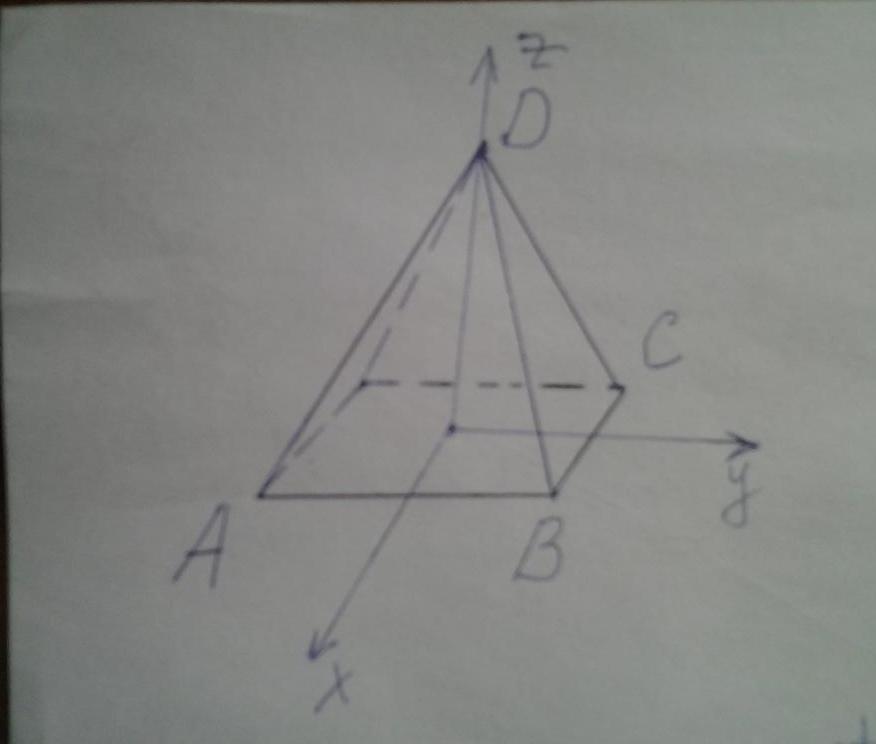
Предположим, что дана правильная пирамида с квадратным основанием. Длина стороны квадрата равна a, высота фигура составляет h. Найдем угол между основанием пирамиды и ее боковой стороной.
Поместим начало координатной системы в центр квадрата. Тогда координаты точек A, B, C, D, показанных на рисунке, будут равны:
Рассмотрим плоскости ACB и ADB. Очевидно, что направляющий вектор n1¯ для плоскости ACB будет равен:
Для определения направляющего вектора n2¯ плоскости ADB поступим следующим образом: найдем произвольные два вектора, которые ей принадлежат, например, AD¯ и AB¯, затем, вычислим их векторное произведение. Его результат даст координаты n2¯. Имеем:
AD¯ = D — A = (0; 0; h) — (a/2; -a/2; 0) = (-a/2; a/2; h);
AB¯ = B — A = (a/2; a/2; 0) — (a/2; -a/2; 0) = (0; a; 0);
n2¯ = [AD¯ × AB¯] = [(-a/2; a/2; h) × (0; a; 0)] = (-a × h; 0; -a2/2).
Поскольку умножение и деление вектора на число не изменяет его направления, то преобразуем полученный n2¯, разделив его координаты на -a, получим:
Мы определили направляющие вектора n1¯ и n2¯ для плоскостей основания ACB и боковой стороны ADB. Остается воспользоваться формулой для угла φ:
φ = arccos (|(n1¯ × n2¯)| / (|n1¯| × |n2¯|)) = arccos (a / (2 × √h2 + a2/4)).
Преобразуем полученное выражение и перезапишем его так:
φ = arccos (a / √(a2 + 4 × h2)).
Мы получили формулу для двугранного угла при основании для правильной четырехугольной пирамиды. Зная высоту фигуры и длину ее стороны, можно рассчитать угол φ. Например, для пирамиды Хеопса, сторона основания которой составляет 230,4 метра, а начальная высота равнялась 146,5 метра, угол φ будет равен 51,8o.
Определить двугранный угол для четырехугольной правильной пирамиды также можно с помощью геометрического метода. Для этого достаточно рассмотреть прямоугольный треугольник, образованный высотой h, половиной длины основания a/2 и апофемой равнобедренного треугольника.
Видео:ДВУГРАННЫЕ УГЛЫ ЧАСТЬ I #shorts #егэ #огэ #математика #профильныйегэСкачать
Повторение теории и решение задач по теме «Двугранный угол. Перпендикулярность плоскостей»
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Тема данного урока: « Повторение теории и решение задач по теме “Двугранный угол. Перпендикулярность плоскостей”». На этом занятии мы повторим теорию, вспомнив определение параллельных прямых и лемму о пересечении параллельными прямыми плоскости. Далее повторим определение о параллельности прямой и плоскости и ее признак. Затем решим несколько задач по теме «Двугранный угол. Перпендикулярность плоскостей».
Видео:№176. Через сторону AD ромба ABCD проведена плоскость ADM так, что двугранный угол BADM равенСкачать
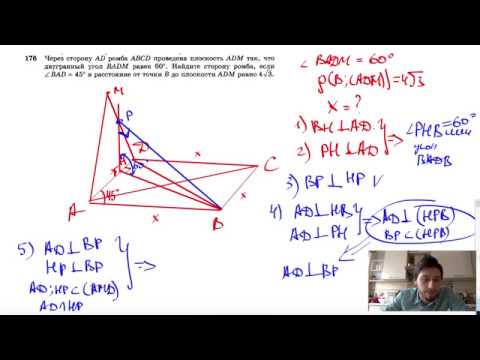
Двугранный угол для четырехугольника
Замечание . Иногда говорят, что двугранный угол α a β образован двумя полуплоскостями α и β , имеющими общую граничную прямую a .
Фигуры, образованные двумя страницами одной книги, двумя соседними гранями куба, — модели двугранного угла.
Для измерения двугранного угла введём понятие его линейного угла. На ребре a двугранного угла α a β отметим произвольную точку O и в гранях α и β проведём из точки O соответственно лучи OA и OB , перпендикулярные ребру a (рис. 96, а ). Угол AOB , образованный этими лучами, называется линейным углом двугранного угла α a β .
Так как OA ⊥ a и OB ⊥ a , то плоскость AOB перпендикулярна прямой a . Это означает, что линейный угол двугранного угла есть пересечение данного двугранного угла и плоскости, перпендикулярной его ребру .
Вследствие произвольного выбора точки O на ребре двугранного угла заключаем, что двугранный угол имеет бесконечное множество линейных углов. Докажем, что все они равны. Действительно, рассмотрим два линейных угла AOB и A 1 O 1 B 1 двугранного угла α a β (рис. 96, б ). Лучи OA и O 1 A 1 лежат в одной грани α и перпендикулярны прямой a — ребру двугранного угла, поэтому они сонаправлены. Аналогично получаем, что сонаправлены лучи OB и O 1 B 1 . Тогда ∠ AOB = ∠ A 1 O 1 B 1 (как углы с сонаправленными сторонами).
Таким образом, нами доказана теорема.
Теорема 27. Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла.
Иначе говоря, все линейные углы данного двугранного угла равны между собой.
Это позволяет ввести следующее определение.
Определение. Величиной двугранного угла называется величина его линейного угла.
Величина двугранного угла, измеренная в градусах, принадлежит промежутку (0 ° ; 180 ° ).
На рисунке 97 изображён двугранный угол, градусная мера (величина) которого равна 30 ° . В этом случае также говорят, что двугранный угол равен тридцати градусам.
Двугранный угол является острым (рис. 98, а ), прямым (рис. 98, б ) или тупым (рис. 98, в ), если его линейный угол соответственно острый, прямой или тупой.
Заметим, что аналогично тому, как и на плоскости, в пространстве определяются смежные (рис. 99, а ) и вертикальные (рис. 99, б ) двугранные углы . При этом справедливы и аналогичные теоремы о величинах этих углов.
Попробуйте доказать самостоятельно следующие два утверждения, важные для решения задач.
На гранях двугранного угла величины α взяты точки A и B ; A 1 и B 1 — проекции этих точек на ребро двугранного угла; AA 1 = a ; BB 1 = b ; A 1 B 1 = h . Тогда
AB = 
.
Если внутри двугранного угла величины α взята точка на расстояниях a и b от граней двугранного угла, то её расстояние от ребра двугранного угла равно 
.
14.2. Угол между двумя плоскостями
Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром (рис. 100). Если величина одного из них равна ϕ , то величины трёх остальных равны соответственно 180 ° – ϕ , ϕ , 180 ° – ϕ (почему?). Наименьшая из этих величин принимается за величину угла между данными пересекающимися плоскостями.
Определение. Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных при их пересечении.
Угол между параллельными или совпадающими плоскостями полагается считать равным нулю.
Если величина угла между плоскостями α и β равна ϕ , то пишут: 
( α ; β ) = ϕ .
Так как двугранный угол измеряется своим линейным углом, то из выше приведённого определения следует, что угол между пересекающимися плоскостями равен углу между пересекающимися прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения (см. рис. 100). Это означает, что величина угла между плоскостями принадлежит промежутку [0 ° ; 90 ° ] .
ЗАДаЧа. Отрезок DM длиной 3,2 перпендикулярен плоскости ромба ABCD ( ∠ ADC — тупой). Диагонали ромба равны 12 и 16. Найти углы между плоскостями:
а) ABC и MBC ; б) AMD и CMD .
Решение. а) Пусть DE — высота ромба ABCD (рис. 101). Тогда по теореме о трёх перпендикулярах ME ⊥ BC и ∠ DEM = ϕ — линейный угол двугранного угла, образованного плоскостями ABC и MBC . Найдём величину этого угла.
По условию задачи DM ⊥ ( ABC ), поэтому ⧌ MDE — прямоугольный, значит, tg ϕ = 
. Так как DE — высота ромба ABCD , то DE = 
, где S — площадь этого ромба. Сторона BC ромба является гипотенузой прямоугольного треугольника BOC , катеты OB и OC которого равны 6 и 8. Значит, BC = 
= 
= 10.
Учитывая, что S = 
• AC • BD = 
•12•16 = 96, находим: DE = 
= 9,6. Тогда tg ϕ = 
= 
= 
, откуда ϕ = arctg 
.
б) Так как отрезок DM — перпендикуляр к плоскости ромба ABCD , то AD ⊥ DM , CD ⊥ DM , значит, ∠ ADC = ψ — линейный угол двугранного угла, образованного пересекающимися плоскостями ADM и CDM . Найдём этот угол.
В треугольнике ACD по теореме косинусов находим
cos ψ = 
= 
= – 
,
откуда ψ = arccos 
.
Ответ: а) arctg 
; б) arccos 
.
📸 Видео
Двугранный угол. Признак перпендикулярности плоскостей. Видеоурок 10. Геометрия 10 классСкачать
22. Двугранный уголСкачать
Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать
ДВУГРАННЫЙ УГОЛ 10 11 класс прямой двугранный уголСкачать
№168. Двугранный угол равен φ. На одной грани этого угла лежит точка, удаленная на расстояние dСкачать
№170. Из вершины В треугольника ABC, сторона АС которого лежит в плоскости а, проведен к этойСкачать
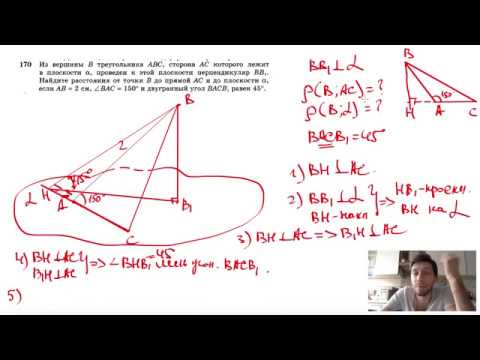
Двугранный уголСкачать
8 класс, 3 урок, ЧетырехугольникСкачать
№190. Дан куб ABCDA1B1C1D1. Найдите следующие двугранные углы: а) АВВ1ССкачать
ГЕОМЕТРИЯ 10 класс : Двугранный угол и Признак перпендикулярности двух плоскостейСкачать
Определить величину двугранного угла при ребре SB между треугольниками SAB и SBC. Замена плоскостейСкачать
Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать
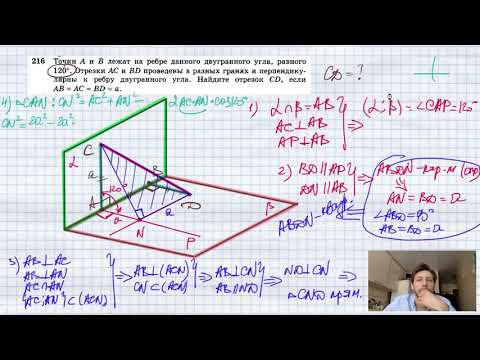
№216. Точки А и В лежат на ребре данного двугранного угла, равного 120°. Отрезки АС и ВD проведены вСкачать
