Две параллельные прямые не пересекаются аксиома или теорема (8 видео)

Новое в блогах

Содержание

Пересекаются ли параллельные или Что говорил Лобачевский?
Что такое аксиома, теорема и доказательство теоремы
Понятие аксиомы
Понятие теоремы
Теоремы без доказательств
Понятия свойств и признаков
Почему параллельные прямые не пересекаются?
🎦 Видео

Видео:Ералаш №8 "Аксиома"Скачать

Пересекаются ли параллельные или Что говорил Лобачевский?

Недавно в посте на околонаучные темы один из комментаторов завел разговор о геометрии Лобачевского (что он ее не понимает) и даже вроде попросил объяснить. Я тогда ограничилась утверждением, что понимаю. Объяснять эту теорию в ограниченных рамках комментария и одним текстом (без рисунков) показалось мне невозможным.

Однако, подумав, я все же решила попробовать дать небольшой популярный экскурс в эту теорию.

Немного предыстории. Геометрия со времен Евклида стала аксиоматической теорией, в которой большинство утверждений доказывалось на основе нескольких постулатов (аксиом). Считалось, что эти аксиомы «очевидны», т.е. отражают свойства реального (физического) пространства.

Одна из этих аксиом вызывала у ученых подозрение: а нельзя ли ее вывести из остальных постулатов? Современная формулировка этой аксиомы такова:

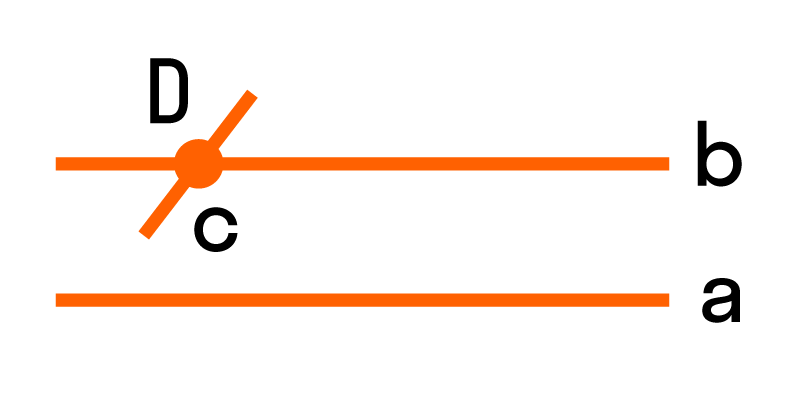
«Через точку, не лежащую на заданной прямой, можно провести не более одной прямой, параллельной ей». То, что одну-то прямую можно провести, является не аксиомой, а теоремой.

При этом «параллельной» называется прямая, не пересекающая данную. Итак, суть аксиомы в том, что такая прямая – одна!

(Распространенное утверждение «Лобачевский доказал, что параллельные прямые могут и пересекаться» — конечно, является вопиюще неправильным! Ведь это бы противоречило их определению!)

Лобачевский, как и многие до него, решил доказать, что это утверждение можно вывести из других аксиом. Для этого он, как это часто делается в математике, выбрал метод «от противного», т.е. предположил, что прямых, не пересекающих данную, больше одной и попытался вывести из этого противоречие с другими фактами. Но чем дальше он развивал теорию, тем больше убеждался, что никакого противоречия не предвидится! Т.е. получалось, что теория с «неправильным» постулатом тоже имеет право на существование!

Конечно, в первое время его выкладки не признавали, смеялись над ним. Именно поэтому великий Гаусс (который пришел к тем же выводам) не рискнул опубликовать свои результаты. Но со временем пришлось признать, что ЧИСТО ЛОГИЧЕСКИ теория Лобачевского ничем не хуже евклидовой.

Один из остроумных способов убедиться в этом – придумать такие «прямые», которые ведут себя как «прямые» Лобачевского. И математики нашли такой пример, и не один.

Пожалуй, самой простой является модель Пуанкаре. Вы можете сами построить ее нехитрыми приборами.

Начертите не листке бумаги прямую. Возьмите циркуль и, ставя его иглу на эту прямую, нарисуйте полуокружности, находящиеся с одной стороны от прямой. Теперь сотрите прямую (и с ней – концевые точки полуокружностей). Так вот, эти полуокружности «без концов» и будут вести себя, как прямые в геометрии Лобачевского!

Действительно, выделим одну полуокружность и точку вне нее. Есть достаточно много полуокружностей, которые не пересекаются с исходной и все проходят через данную точку. Среди них выделяются две: они касаются нашей исходной «прямой» в концевых точках (которые мы, как Вы помните, стерли) Т.е. реального пересечения не происходит. Эти две окружности задают «границы», между которыми находятся все прямые, не пересекающие данную. Их – бесконечное количество.

Можно заметить, что треугольники в этой модели не такие, как на плоскости (евклидовой): сумма их углов меньше 180 градусов! Впрочем, чем меньше треугольник, тем больше сумма его углов. В «малом», на небольших расстояниях, геометрия Лобачевского практически совпадает с геометрией Евклида. Поэтому, вообще говоря, мы не сможем «экспериментально» отличить одну от другой, если окажется, что доступные нам (космические) расстояния– малы для этой цели.

Впрочем, в наше время ни физики, ни, тем более, математики, не пытаются воспринимать геометрию Лобачевского как модель «реального», физического пространства. Математики поняли, что все, что они могут сказать: если верны такие-то аксиомы, то верны и такие-то теоремы. Ну, а что такое «множества», «точки», «прямые», «углы», «расстояния», и т.п. – этого мы не знаем! Прямо как у Станислава Лема: «Сепульки – это объекты для сепулькирования»

«Говорят, Бертран Рассел определил математику как науку, в которой мы никогда не знаем, о чем говорим, и насколько правильно то, что мы говорим. Известно, что математика широко применяется во многих других областях науки. [ … ] Таким образом, одна из главных функций математического доказательства – создание надежной основы для проникновения в суть вещей.»

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Что такое аксиома, теорема и доказательство теоремы

О чем эта статья:

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Понятие аксиомы

Аксиома — это правило, которое считают верным и которое не нужно доказывать. В переводе с греческого «аксиома» значит принятое положение — то есть взяли и договорились, что это истина, с которой не поспоришь.

Аксиоматический метод — это подход к получению знаний, при котором сначала разрабатывают аксиомы, а потом с их помощью формулируют новые теории.

Синоним аксиомы — постулат. Антоним — гипотеза.

Основные аксиомы евклидовой геометрии

Через любые две точки проходит единственная прямая.
Каждая точка на прямой разбивает эту прямую на две части так, что точки из разных частей лежат по разные стороны от данной точки. А точки из одной части лежат по одну сторону от данной точки.
На любом луче от его начала можно отложить только один отрезок, равный данному.
Отрезки, полученные сложением или вычитанием соответственно равных отрезков — равны.
Каждая прямая на плоскости разбивает эту плоскость на две полуплоскости. При этом если две точки принадлежат разным частям, то отрезок, который соединяет эти две точки, пересекается с прямой. Если две точки принадлежат одной части, то отрезок, соединяющий эти точки, не пересекается с прямой.
От любого луча на плоскости в заданную сторону можно отложить только один угол, который равен данному. Все развернутые углы равны.
Углы равны, если они получились путем сложения или вычитания соответственно равных углов.

Учить наизусть эти аксиомы не обязательно. Главное — помнить о них и держать под рукой, чтобы при доказательстве теоремы сослаться на одну из них.

А теперь давайте рассмотрим несколько аксиом из геометрии за 7 и 8 класс.

Самая известная аксиома Евклида — аксиома о параллельных прямых. Звучит она так:

Это значит, что если дана прямая и любая точка, которая не лежит на этой прямой, то через неё можно провести только одну единственную прямую, которая будет параллельна этой первой данной прямой.

У этой аксиомы два следствия:

прямая, которая пересекает одну параллельную прямую, обязательно пересекает и другую;
если две прямые параллельны третьей, то между собой они также параллельны.

Аксиома Архимеда заключается в том, что, если отложить достаточное число раз меньший из двух отрезков, то можно покрыть больший из них. Звучит так:

Если на прямой есть меньший отрезок А и больший отрезок B, то, можно сложить А достаточное количество раз, чтобы покрыть B.

На картинке можно увидеть, как это выглядит:

Из этого следует, что не существует бесконечно малых и бесконечно больших величин. В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Понятие теоремы

Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.

Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.

Состав теоремы: условие и заключение или следствие.

Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.

Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.

Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.

Примеры следствий из аксиомы о параллельности прямых:

если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую;
если две прямые параллельны третьей прямой, то они параллельны.

Доказательство теоремы — это процесс обоснования истинности утверждения.

Каждая доказанная теорема служит основанием доказательства для следующей теоремы. Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам.

Способы доказательства геометрических теорем

Синтетический или синтез — метод, при котором данное предложение выступает, как необходимое следствие другого, уже доказанного.
Аналитический или анализ — обратный синтезу способ. Рассуждения всегда начинаются с доказываемой теоремы и закачиваются другой известной истиной.

Часть аналитического способа — доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.

Приемы для доказательства в геометрии:

Способ наложения — когда одну геометрическую величину накладывают на другую. Этим способом убеждаются в равенстве или неравенстве геометрических протяжений в зависимости от того, совмещаются они или нет при наложении.
Способ пропорциональности — применение свойств пропорций. Этот способ пригодится для доказательства теорем про подобные фигуры и пропорциональные отрезки.
Способ пределов — когда вместо данной величины берут свойства другой, близкой к ней. А потом перекладывают эти выводы на исходные данные.

Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.

Прямая и обратная теорема взаимно-обратные. Например:

прямая теорема: в треугольнике против равных сторон лежат равные углы.
обратная теорема: в треугольнике против равных углов лежат равные стороны.

В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов. А во второй всё наоборот.

Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.

Вот, как выглядит взаимное отношение теорем на примере:

Прямая: если при пересечении двух прямых третьей соответственные углы равны, то данные прямые параллельны.
Обратная: если две прямые параллельны, то при пересечении их третьей, соответственные углы равны.
Противоположная: если при пересечении двух прямых третьей соответственные углы не равны, прямые не параллельны.
Обратная противоположной: если прямые не параллельны, соответственные углы не равны.

В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Видео:Параллельность прямых. 10 класс.Скачать

Теоремы без доказательств

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

Доказательств может быть несколько. Одно из них звучит так: если построить квадраты на сторонах прямоугольного треугольника, то площадь большего из них равна сумме площадей меньших квадратов. На картинке понятно, как это работает:

Теорема косинусов: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. В виде формулы это выглядит так:

где a, b и c — стороны плоского треугольника,

α — угол, противолежащий стороне а.

Следствия из теоремы косинусов:

при b² + c² – a² > 0 угол α будет острым;
при b² + c² – a² = 0 угол α будет прямым, что соответствуем теореме Пифагора;
при b² + c² – a²

Видео:7 класс, 28 урок, Аксиома параллельных прямыхСкачать

Понятия свойств и признаков

У нас есть список аксиом и мы уже знаем, что такое теорема и как ее доказывать. Есть два типа утверждений среди теорем, которые часто встречаются при изучении новых фигур: свойства и признаки.

Свойства и признаки — понятия из обычной жизни, которые мы часто используем.

Свойство — такое утверждение, которое должно выполняться для данного типа объектов. У ноутбука есть клавиатура — это свойство есть у каждого ноутбука. А у электронной книги такого свойства нет.

Примеры геометрических свойств мы уже знаем: у квадрата все стороны равны. Это верно для любого квадрата, поэтому это — свойство.

Такое свойство можно встретить у другого четырехугольника. И клавиатура может быть на других устройствах, помимо ноутбука. Из этого следует, что свойства не обязательно должны быть уникальными.

Признак — это то, по чему мы однозначно распознаем объект.

Звезды в темном небе — признак того, что сейчас ночь. Если человек ходит с открытым зонтом — это признак того, что сейчас идет дождь. При этом ночью не обязательно должны быть видны звезды, иногда может быть облачно. Значит это не свойство ночи.

А теперь вернемся к геометрии и рассмотрим четырехугольник ABCD, в котором AB = BD = 10 см.

Является ли равенство диагоналей признаком прямоугольника? У такого четырехугольника, где AB = BD, диагонали равны, но он не является прямоугольником. Это свойство, но не его признак.

Но если в четырехугольнике противоположные стороны параллельны AB || DC и AD || BC и диагонали равны AB = BD, то это уже верный признак прямоугольника. Смотрите рисунок:

Иногда свойство и признак могут быть эквивалентны. Лужи — это верный признак дождя. У других природных явлений не бывает луж. Но если приходит дождь, то лужи на асфальте точно будут. Значит, лужи — это не только признак, но и свойство дождя.

Такие утверждения называют необходимым и достаточным признаком.

Видео:Геометрия 7 класс (Урок№20 - Аксиома параллельных прямых.)Скачать

Почему параллельные прямые не пересекаются?

На первый взгляд этот вопрос может показаться довольно глупым. Ну как могут пересекаться параллельные прямые? Хотя, если обратиться к разным видам геометрии, то можно заметить следующую особенность Параллельные прямые существуют лишь в евклидовой и Лобачевского – Бони геометриях. В геометрии Римана их вообще нет. Там все прямые пересекаются. Есть еще геометрия, которая имеет дело с непостоянной кривизны пространством, но на ней мы останавливаться не будем. В данном случае нас интересует, евклидова геометрия, которую, как раз, и изучают в школе.

И так, согласно евклидовой геометрии через точку на плоскости можно провести всего одну параллельную прямую, которая не будет пересекаться с искомой. Этот факт здесь является аксиомой, и не требует доказательств. Данная аксиома гласит, что в евклидовой геометрии параллельные прямые не пересекаются!

И все-таки несмотря на то, что это аксиома, давайте попробуем разобраться в сути данного вопроса. Все дело в том, что в евклидовой геометрии используется плоскость, с радиусом кривизны, равной бесконечности. Геометрия Лобачевского базируется на несколько ином утверждении, что не все плоскости имеют бесконечный радиус кривизны. В качестве примера можно привести нашу планету, поверхность которой имеет сферическую форму.

Получается, что под параллельными прямыми, Евклид подразумевал две прямые линии, которые находятся в одной плоскости, и при этом не имеют общих точек. Это утверждение, в свою очередь, породило ряд других. Если эти две прямые пересечь другой плоскостью, то они будут считаться параллельными в том случае, если образуемые при этом углы будут равными. При таком раскладе они никогда не пересекутся. Именно таким образом можно доказать и пятый постулат Евклида. То есть, через точку, которая не лежит на данной прямой, можно провести всего одну, параллельную ей линию.