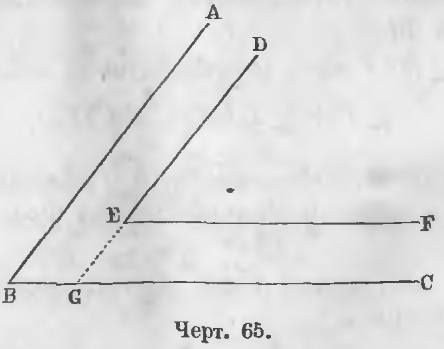Определение параллельных прямых. Параллельными называются две прямые линии, лежащие в одной плоскости и не пересекающиеся на всем своем протяжении.
Прямые AB и CD (черт. 57) будут параллельными. То обстоятельство, что они параллельны, выражают иногда письменно: AB || CD.
Теорема 34. Две прямые, перпендикулярные к одной и той же третьей, параллельны.
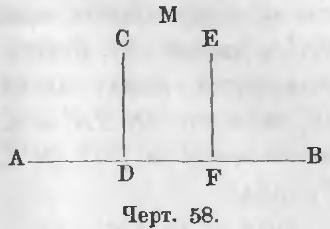
Даны прямые CD и EF перпендикулярные к AB (черт. 58)
CD ⊥ AB и EF ⊥ AB.
Требуется доказать, что CD || EF.
Доказательство. Если бы прямые CD и EF не были параллельны, они пересеклись бы в какой нибудь точке M. В этом случае из точки M на прямую AB были бы опущены два перпендикуляра, что невозможно (теорема 11), следовательно прямая CD || EF (ЧТД).
Теорема 35. Две прямые, из которых одна перпендикулярна, а другая наклонна к третьей, всегда пересекаются.
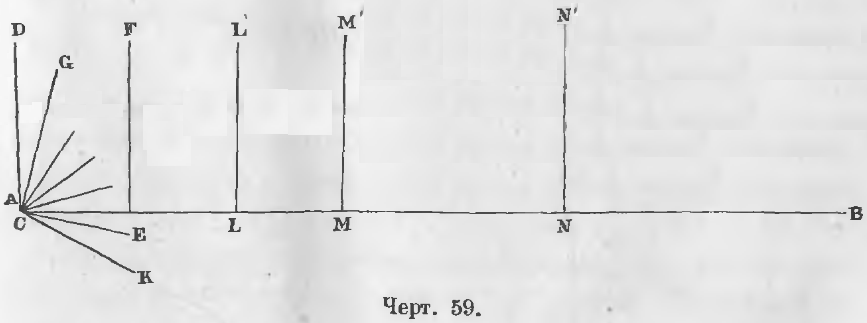
Даны две прямые EF и CG, из которых EF ⊥ AB, а CG наклонна к AB (черт. 59).
Требуется доказать, что CG встретится с линией EF или что CG не параллельна EF.
Доказательство. Из точки C восставим к линии AB перпендикуляр CD, тогда при точке C образуется угол DCG, который станем повторять столько раз, чтобы линия CK упала ниже линии AB. Положим, что мы для этого угол DCG повторим n раз, как что
Подобным же образом отложим на прямой AB прямую CE тоже n раз так что CN = nCE.
Из точек C, E, L, M, N восставим перпендикуляры LL’, MM’, NN’. Пространство, содержащееся между двумя параллельными отрезками CD, NN’ и отрезком CN, будет в n раз больше пространства, заключающегося между двумя перпендикулярами CD, EF и отрезком CE, так что DCNN’ = nDCEF.
Пространство, заключающееся в угол DCK, содержит в себе пространство DCNN’, следовательно,
DCK > CDNN’ или
nDCG > nDCEF, откуда
DCG > DCEF.
Последнее неравенство может иметь место только тогда, когда прямая CG выйдет при своем продолжении из пределов пространства DCEF, т. е. когда прямая CG встретится с прямой EF, следовательно прямая CG не параллельна CF (ЧТД).
Теорема 36. Прямая, перпендикулярная к одной из параллельных, перпендикулярна и к другой.
Даны две параллельные прямые AB и CD и прямая EF перпендикулярная к CD (черт. 60).
Требуется доказать, что EF ⊥ AB.
Доказательство. Если бы прямая AB была наклонна к EF, то две прямые CD и AB пересеклись бы, ибо CD ⊥ EF и AB наклонна к EF (теорема 35), и прямые AB и CD не были бы параллельны, что противоречило бы данному условию, следовательно, прямая EF перпендикулярна CD (ЧТД).
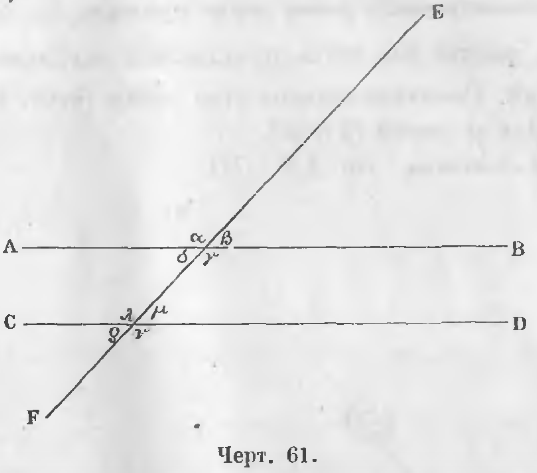
Углы, образуемые пересечением двух прямых третьей прямой. При пересечении двух прямых AB и CD третьей прямой EF (черт. 61) образуется восемь углов α, β, γ, δ, λ, μ, ν, ρ . Эти углы получают особые названия.
Четыре угла α, β, ν и ρ называются внешними.
Четыре угла γ, δ, λ, μ называются внутренними.
Четыре угла β, γ, μ, ν и четыре угла α, δ, λ, ρ называются односторонними, ибо лежат по одну сторону прямой EF.
Кроме того, углы, будучи взяты попарно, получают следующие названия:
Углы β и μ называются соответственными . Кроме этой пары такими же соответственными углами будут пары углов: γ и ν, α и λ, δ и ρ.
П ары углов δ и μ , а также γ и λ называются внутренними накрест-лежащими .
Пары углов β и ρ , а также α и ν называются внешними накрест-лежащими .
Пары углов γ и μ , а также δ и λ называются внутренними односторонними .
Пары углов β и ν , а также α и ρ называются внешними односторонними .
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Условия параллельности двух прямых
Теорема 37. Две прямые параллельны, если при пересечении их третьей у них равны: 1) соответственные углы, 2) внутренние накрест-лежащие, 3) внешние накрест-лежащие, и, наконец, если 4) сумма внутренних односторонних равна двум прямым, 5) сумма внешних односторонних равна двум прямым.
Докажем каждую из этих частей теоремы отдельно.
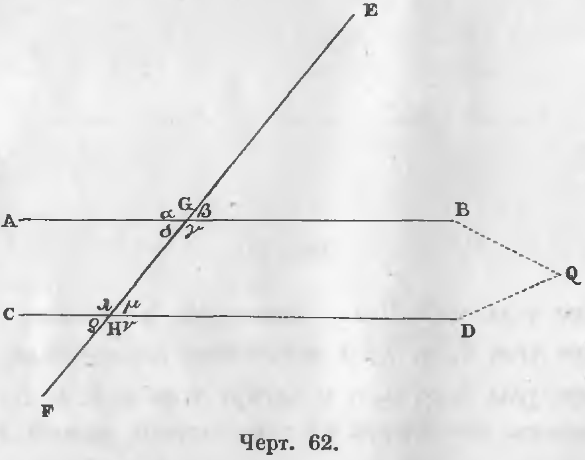
1-й случай. Соответственные углы равны (черт. 62).
Дано. Углы β и μ равны.
Требуется доказать, что AB || CD.
Доказательство. Если бы линии AB и CD пересекались в точке Q, то получился бы треугольник GQH, у которого внешний угол β равнялся бы внутреннему углу μ, что противоречило бы теореме 22, следовательно, прямые AB и CD не пересекаются или AB || CD (ЧТД).
2-й случай. Внутренние накрест-лежащие углы равны, то есть δ = μ.
Доказательство. δ = β как вертикальные, δ = μ по условию, следовательно, β = μ. То есть соответственные углы равны, а в этом случае линии параллельны (1-й случай).
3-й случай. Внешние накрест-лежащие углы равны, то есть β = ρ.
Доказательство. β = ρ по условию, μ = ρ как вертикальные, следовательно, β = μ, т. к. соответственные углы равны. Отсюда следует, что AB || CD (1-й случай).
4-й случай. Сумма внутренних односторонних равна двум прямым или γ + μ = 2d.
Доказательство. β + γ = 2d как сумма смежных, γ + μ = 2d по условию. Следовательно, β + γ = γ + μ, откуда β = μ. Соответственные углы равны, следовательно, AB || CD.
5-й случай. Сумма внешних односторонних равна двум прямым, то есть β + ν = 2d.
Доказательство. μ + ν = 2d как сумма смежных, β + ν = 2d по условию. Следовательно, μ + ν = β + ν, откуда μ = β. Соответственные углы равны, следовательно, AB || CD.
Таким образом, во всех случаях AB || CD (ЧТД).
Теорема 38 (обратная 37). Если две прямые параллельны, то при пересечении их третьей прямой будут равны: 1) внутренние накрест-лежащие углы, 2) внешние накрест-лежащие, 3) соответственные углы и равны двум прямым 4) сумма внутренних односторонних и 5) сумма внешних односторонних углов.
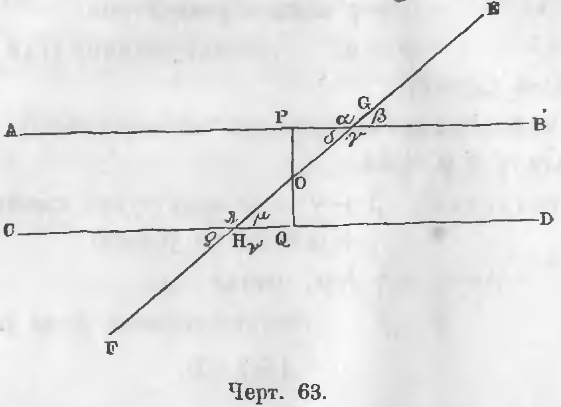
Даны две параллельные прямые AB и CD, то есть AB || CD (черт. 63).
Требуется доказать, что все вышеописанные условия выполняются.
1-й случай. Пересечем две параллельные прямые AB и CD третьей наклонной прямой EF. Обозначим через G и Н точки пересечения прямых AB и CD прямой EF. Из точки O середины прямой GH опустим перпендикуляр на прямую CD и продолжим его до пересечения с прямой AB в точке P. Прямая OQ перпендикулярная к CD перпендикулярна и к AB (теорема 36). Прямоугольные треугольника OPG и OHQ равны, ибо OG = OH по построению, ∠ HOQ = ∠ POG как вертикальные углы, следовательно, OP = OQ.
Отсюда следует, что δ = μ, т. е. внутренние накрест-лежащие углы равны.
2-й случай. Если AB || CD, то δ = μ, а так как δ = β, и μ = ρ, то β = ρ, т. е. внешние накрест-лежащие углы равны.
3-й случай. Если AB || CD, то δ = μ, а так как δ = β, то и β = μ, следовательно, соответственные углы равны.
4-й случай. Если AB || CD, то δ = μ, а так как δ + γ = 2d, то и μ + γ = 2d, т. е. сумма внутренних односторонних равна двум прямым.
5-й случай. Если AB || CD, то δ = μ.
Так как μ + ν = 2d, μ = δ = β, следовательно, ν + β = 2d, т. е. сумма внешних односторонних равна двум прямым.
Из этих теорем вытекает следствие. Через точку можно провести только одну прямую, параллельную другой прямой.
Теорема 39. Две прямые, параллельные третьей, параллельны между собой.
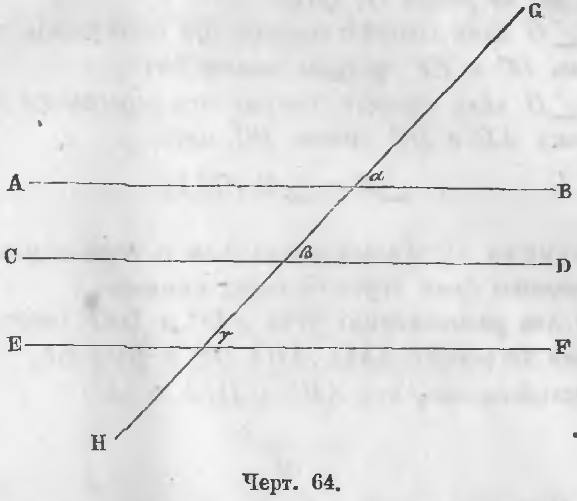
Даны три прямые (черт. 64) AB, CD и EF, из которых AB || EF, CD || EF.
Требуется доказать, что AB || CD.
Доказательство. Пересечем эти прямые четвертой прямой GH.
Если AB || EF, то ∠ α = ∠ γ как соответственные. Если CD || EF, то ∠ β = ∠ γ также как соответственные. Следовательно, ∠ α = ∠ β .
Если же соответственные углы равны, то прямые параллельны, следовательно, AB || CD (ЧТД).
Теорема 40. Одноименные углы с параллельными сторонами равны.
Даны одноименные (оба острые или оба тупые) углы ABC и DEF, их стороны параллельны, т. е. AB || DE, BC || EF (черт. 65).
Требуется доказать, что ∠ B = ∠ E.
Доказательство. Продолжим сторону DE до пересечения ее с прямой BC в точке G, тогда
∠ E = ∠ G как соответственные от пересечения сторон параллельных BC и EF третьей прямой DG.
∠ B = ∠ G как соответственные от пересечения параллельных сторон AB и DG прямой BC, следовательно,
Теорема 41. Разноименные углы с параллельными сторонами дополняют друг друга до двух прямых.
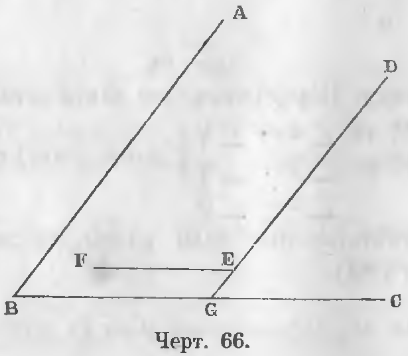
Даны два разноименные угла ABC и DEF (черт. 66) с параллельными сторонами, следовательно, AB || DE и BC || EF.
Требуется доказать, что ABC + DEF = 2d.
Доказательство. Продолжим прямую DE до пересечения с прямой BC в точке G.
∠ B + ∠ DGB = 2d как сумма внутренних односторонних углов, образуемых пересечением параллельных AB и DG третьей прямой BC.
∠ DGB = ∠ DEF как соответственные, следовательно,
∠ B + ∠ DEF = 2d (ЧТД).
Теорема 42. Одноименные углы с перпендикулярными сторонами равны и разноименные дополняют друг друга до двух прямых.
Рассмотрим два случая: когда А) углы одноименны и когда B) они разноименны.
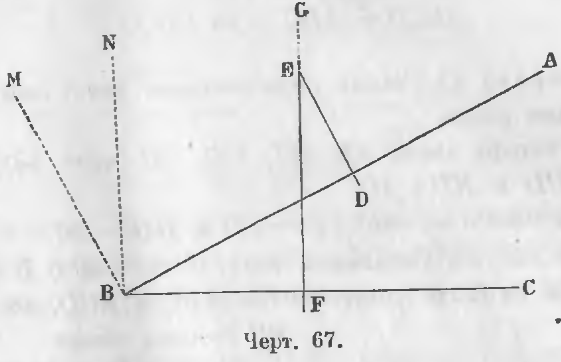
1-й случай. Стороны двух одноименных углов DEF и ABC (черт. 67) перпендикулярны, т. е. DE ⊥ AB, EF ⊥ BC.
Требуется доказать, что ∠ DEF = ∠ ABC.
Доказательство. Проведем из точки B прямые BM и BN параллельно прямым DE и EF так, что
Прямые эти также перпендикулярны к сторонам данного угла ABC, т. е.
BM ⊥ AB и BN ⊥ BC.
Так как ∠ NBC = d, ∠ MBA = d, то
Вычтя из обоих частей равенства (а) по углу NBA, находим
Так как углы MBN и DEF одноименны и с параллельными сторонами, то они равны (теорема 40).
Из равенств (a) и (b) вытекает равенство
2-й случай. Углы GED и ABC с перпендикулярными сторонами разноименны.
Требуется доказать, что ∠ GED + ∠ ABC = 2d (черт. 67).
Доказательство. Сумма углов GED и DEF равна двум прямым.
GED + DEF = 2d
DEF = ABC, следовательно,
GED + ABC = 2d (ЧТД).
Теорема 43. Части параллельных прямых между другими параллельными равны.
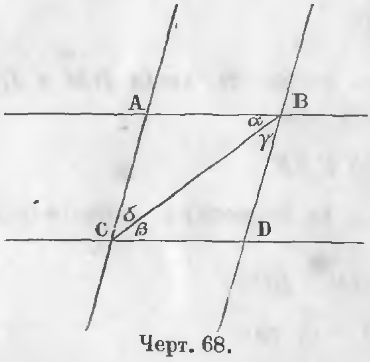
Даны четыре прямые AB, BD, CD, AC (черт. 68), из которых AB || CD и BD || AC.
Требуется доказать, что AB = CD и BD = AC.
Доказательство. Соединив точку C с точкой B отрезком BC, получим два равных треугольника ABC и BCD, ибо
BC — сторона общая,
∠ α = ∠ β (как внутренние накрест-лежащие от пересечения параллельных прямых AB и CD третьей прямой BC),
∠ γ = ∠ δ (как внутренние накрест-лежащие от пересечения параллельных прямых BD и AC прямой BC).
Таким образом, треугольники имеют по равной стороне и по двум равным углам, лежащим на ней.
Против равных углов α и β лежат равные стороны AC и BD, и против равных углов γ и δ — равные стороны AB и CD, следовательно,
AC = BD, AB = CD (ЧТД).
Теорема 44. Параллельные прямые на всем своем протяжении находятся на равном расстоянии друг от друга.
Расстояние точки от прямой определяется длиной перпендикуляра, опущенного из точки на прямую. Чтобы определить расстояние каких угодно двух точек A и B параллельной AB от CD, из точек A и B опустим перпендикуляры AC и BD.
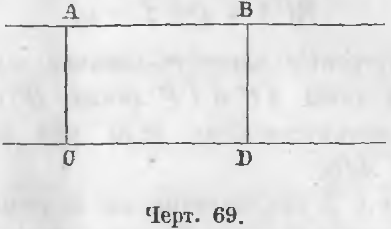
Дана прямая AB параллельная CD, отрезки AC и BD перпендикулярны к прямой CD, т. е. AB || CD, AC ⊥ DC, BD ⊥ CD (черт. 69).
Требуется доказать, что AC = BD.
Доказательство. Прямые AC и BD, будучи обе перпендикулярными к CD, параллельны, а следовательно, AC и BD как части параллельных между параллельными, равны, т. е. AC = BD (ЧТД).
Теорема 45 (обратная 43). Если противоположные части четырех пересекающихся прямых равны, то эти части параллельны.
Даны четыре пересекающиеся прямые, противоположные части которых равны: AB = CD и BD = AC (черт. 68).
Требуется доказать, что AB || CD и BD || AC.
Доказательство. Соединим точки B и C прямой BC. Треугольники ABC и BDC равны, ибо
BC — общая сторона,
AB = CD и BD = AC по условию.
AC || BD, AB || CD (ЧТД).
Теорема 46. Сумма углов треугольника равна двум прямым.
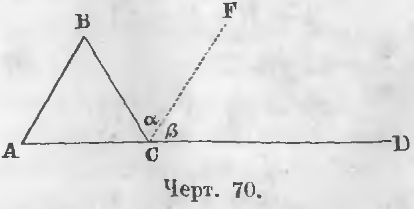
Дан треугольник ABC (черт. 70).
Требуется доказать, что A + B + C = 2d.
Доказательство. Проведем из точки C прямую CF параллельную стороне AB. При точке C образуется три угла BCA, α и β . Сумма их равна двум прямым:
α = B (как внутренние накрест-лежащие углы при пересечении параллельных прямых AB и CF прямой BC);
β = A (как соответственные углы при пересечении прямых AB и CF прямой AD).
Заменяя углы α и β их величинами, получим:
BCA + A + B = 2d (ЧТД).
Из этой теоремы вытекают следующие следствия:
Следствие 1 . Внешний угол треугольника равен сумме внутренних не смежных с ним.
Доказательство . Действительно, из чертежа 70,
Так как ∠ α = ∠ B, ∠ β = ∠ A, то
Следствие 2 . В прямоугольном треугольнике сумма острых углов равна прямому.
Действительно, в прямоугольном треугольнике (черт. 40)
A + B + C = 2d, A = d, следовательно,
B + C = d.
Следствие 3 . В треугольнике не может быть больше одного прямого или одного тупого угла.
Следствие 4 . В равностороннем треугольнике каждый угол равен 2/3 d .
Действительно, в равностороннем треугольнике
Видео:№211. Две параллельные прямые пересечены секущей. Докажите, что: а) биссектрисыСкачать

Параллельные прямые
Две прямые называются параллельными, если они лежат на одной плоскости и не пересекаются, сколько бы их ни продолжали:
Для обозначения параллельности двух прямых используется знак || , обозначающий параллельность. Запись AB || CD (или a || b) читается так: прямая AB параллельна прямой CD (или прямая a параллельна прямой b ).
Видео:№215. Параллельные прямые АВ и CD лежат в разных гранях двугранного угла, равного 60°. Точки А и DСкачать

Пересечение параллельных прямых
Если несколько параллельных прямых пересечь прямой линией, то эта прямая пересечёт каждую из параллельных прямых под одним и тем же углом:
Если прямые перпендикулярны одной и той же прямой, то они параллельны.
Обе прямые m и n перпендикулярны прямой a, значит прямые m и n параллельны.
Видео:Параллельные прямые циркулемСкачать

Построение параллельных прямых
На свойстве пересечения прямой линией параллельных прямых основан способ их построения с помощью угольника и линейки.
Если прямая линия уже построена, то для постройки второй линии, параллельной первой, надо расположить сторону угольника вдоль построенной линии и зафиксировать это положение линейкой:
Передвинув угольник вдоль линейки, можно провести ещё одну прямую, которая будет параллельна первой.
Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Взаимное положение прямых
Как известно, прямые в пространстве могут быть пересекающимися, параллельными или скрещивающимися. Рассмотрим эти случаи.
Пересекающиеся прямые. Наглядное изображение двух прямых АВ и CD. пересекающихся в точке К, приведено на рисунке 2.10, их чертеж в системе V, Н — на рисунке 2.11.
Если прямые пересекаются, то их одноименные проекции пересекаются между собой, а проекции точек пересечения лежат на одной линии связи.


Для прямых, кроме профильных, в системе V, Н справедливо и обратное утверждение:
если в системе V, Н тонки пересечения одноименных проекций прямых, кроме профильных, лежат на одной линии связи, то прямые пересекаются.
Если в системе V, Н одна из рассматриваемых прямых профильная, то, чтобы ответить на вопрос, пересекаются ли прямые, следует построить их профильные проекции.
Примеры чертежей пересекающихся и непересекаюших- ся (скрещивающихся) прямых, из которых одна с проекциями a’b’, ab, а»Ь“— профильная, показаны на рисунках 2.12 и 2.13.
На рисунке 2.12 все три проекции к’, к, к» точки К прямой CD принадлежат и трем одноименным проекциям a’b’, ab и а»Ь» прямой АВ, т. е. прямые пересекаются.
На рисунке 2.13 профильная проекция Г точки L прямой CD не принадлежит профильной проекции а»Ь», следовательно, прямые АВ и CD не пересекаются (см. также рис. 2.7, а).
На рисунке 2.14 показаны прямые, две проекции которых пересекаются в одной точке, а две другие проекции сливаются в одну линию. Это означает, что обе прямые принадлежат плоскости Р, перпендикулярной плоскости Н (рис. 2.15).
Частный случай ортогональной проекции двух взаимно перпендикулярных прямых, из которых одна параллельна плоскости проекций, а другая не перпендикулярна ей, рассмотрен в § 1.3 (см. рис. 1.10).
Чертеж прямого угла АВС со стороной ВС, параллельной плоскости Я, приведен на рисунке 2.16. Горизонтальная проекция Ьа стороны ВА перпендикулярна горизонтальной проекции Ьс стороны ВС.
Эта особенность проецирования прямого угла упрощает решение ряда задач. Например, пусть требуется начертить перпендикуляр из точки с проекциями а’, а к прямой с проекциями Ь’с’, Ьс, параллельной плоскости V (рис. 2.17). Для этого из точки а‘ проводим перпендикуляр а’т’ к Ь’с’. Построив проекцию т, проводим горизонтальную проекцию am перпендикуляра.
Это свойство будет широко использовано в дальнейшем.
Заметим, что проекция любого угла в зависимости от положения его плоскости может представлять собой острый, прямой или тупой угол (или прямую линию, если плоскость угла перпендикулярна плоскости проекций). Если угол не прямой и одна сторона его параллельна плоскости проекций, то на эту плоскость острый угол проецируется также в виде острого угла меньшей величины, тупой угол — в виде тупого угла большей величины.
Параллельные прямые. Если в пространстве прямые параллельны, то их одноименные проекции параллельны между собой. Действительно (рис. 2.18), проецирующие плоскости Р и Q, проведенные через параллельные прямые АВ и CD, параллельны между собой. С плоскостью проекций Я они пересекаются по параллельным прямым ab и cd — проекциям прямых АВ и CD на плоскости Я. Однако из параллельности проекций не всегда следует параллельность прямых.
В примере на рисунке 2.19 проекции a’b’, e’f’, ab, ef профильных прямых АВ и EF между собой параллельны. Однако
зо из взаимного положения их профильных проекций видно, что сами прямые не параллельны.
Для прямых общего положения эти условия параллельности следующие:
если одноименные проекции прямых общего положения параллельны в системе двух плоскостей проекций, то прямые параллельны (рис. 2.20).
Для прямых частного положения:
если одноименные проекции прямых параллельны одной из осей проекций, то прямые параллельны при условии параллельности одноименных проекций на той плоскости проекций, которой параллельны прямые.
По рисунку 2.21 заключаем, что профильные прямые 5—6 и 7—8 параллельны, так как параллельны их профильные проекции 5″ 6″ и 7″ 8″.
Скрещивающиеся прямые. Скрещивающиеся прямые не имеют общих точек. Наглядное изображение двух скрещивающихся прямых АВ и CD общего положения дано на рисунке 2.22, их чертеж — на рисунке 2.23. С точкой пересечения одноименных Рис 2.21 проекций ab и cd (рис. 2.22) совпада
ют проекции к и / двух точек К и L, принадлежащих различным прямым CD и А В.
Точки пересечения одноименных проекций скрещивающихся прямых не лежат на одной линии связи (рис. 2.23).
Интересен вопрос: какая из изображенных на чертеже прямых выше другой или ближе другой к наблюдателю? Это определяют путем анализа положения определенных точек этих прямых.
На рисунке 2.22 видно, что при взгляде сверху по указанной стрелке точка L на прямой АВ закрывает точку К (проекция точки К на плоскости Я показана поэтому в скобках). Соответственно и на чертеже, приведенном на рисунке 2.23, видно, что фронтальная проекция Г выше фронтальной проекции к и при взгляде сверху по стрелке N при проецировании на плоскость Я точка L закрывает точку К (горизонтальная проекция к показана в скобках). На плоскости V совпадают фронтальные проекции Г и 2‘ точек прямых А В и CD. При взгляде спереди по стрелке М видно, что точка 1 прямой АВ

Рис. 2.22 Рис. 2.23
находится ближе к наблюдателю, и при проецировании на плоскость Кточка / прямой АВ закрывает точку 2 прямой CD (фронтальная проекция 2′ точки 2 показана в скобках).
Рассмотренные точки скрещивающихся прямых, проекции которых на одной из плоскостей совпадают, в литературе иногда называют конкурирующими точками.
- 01. При каком положении относительно плоскостей проекций прямую называют прямой общего положения?
- 2. Как выражается соотношение между проекцией отрезка прямой и самим отрезком?
- 3. Как расположена прямая в системе Н, V, W если все три проекции отрезка этой прямой равны между собой?
- 4. Как построить профильную проекцию отрезка прямой общего положения по данным фронтальной и горизонтальной проекциям?
- 5. Как располагается фронтальная проекция отрезка прямой линии, если его горизонтальная проекция равна самому отрезку?
- 6. Как располагается горизонтальная проекция отрезка прямой линии, если его фронтальная проекция равна самому отрезку?
- 7. Как разделить на чертеже отрезок прямой линии в заданном отношении?
- 8. Как построить на чертеже треугольники для определения длины отрезка прямой линии общего положения и ее углов с горизонтальной и фронтальной плоскостями проекций?
- 9. Какое свойство параллельного проецирования относится к параллельным прямым?
- 10. Можно ли по фронтальной и горизонтальной проекциям двух профильных прямых определить, параллельны ли между собой эти прямые?
- 11. Как следует истолковать точку пересечения проекций двух скрещивающихся прямых?
- 12. В каком случае прямой угол проецируется в виде прямого угла?
🔍 Видео
Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

№44. Прямые ОВ и CD параллельные, а ОА и CD — скрещивающиеся прямые.Скачать

Параллельные прямые. 6 класс.Скачать

10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

№16. Параллельные прямые a и b лежат в плоскости α. Докажите,Скачать

Параллельность прямых. 10 класс.Скачать

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. §13 геометрия 7 классСкачать

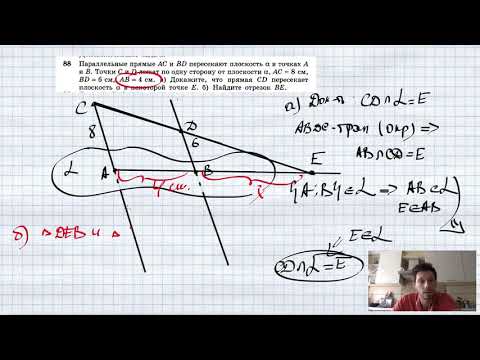
№88. Параллельные прямые АС и BD пересекают плоскость α соответственно в точках А и В. Точки С и DСкачать
Параллельные прямые — Признак Параллельности Прямых и Свойства УгловСкачать

№39. Докажите, что если АВ и CD скрещивающиеся прямые, то AD и ВС также скрещивающиеся прямые.Скачать

Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать

6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать