Наибольший периметр треугольника вписанного в окружность (7 видео)

Треугольник вписанный в окружность

Содержание

Определение
Формулы
Радиус вписанной окружности в треугольник
Радиус описанной окружности около треугольника
Площадь треугольника
Периметр треугольника
Сторона треугольника
Средняя линия треугольника
Высота треугольника
Свойства
Доказательство
Как найти периметр треугольника
Определение
Как узнать периметр треугольника
Скачать онлайн таблицу
Решение геометрических задач на нахождение наибольшего и наименьшего значений с помощью производной
Планиметрические задачи
💡 Видео

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

Периметр треугольника вписанного в окружность,
если известны все стороны:

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

Средняя линия треугольника вписанного
в окружность, если известно основание:

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

Высота треугольника вписанного в окружность,
если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

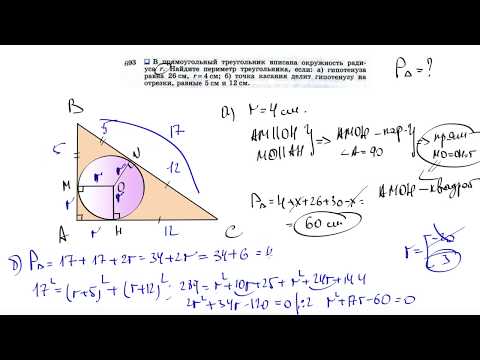
Видео:№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать

Свойства

Центр вписанной в треугольник окружности
находится на пересечении биссектрис.
В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну.
Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора.
Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров.
Все вершины треугольника, вписанного
в окружность, лежат на окружности.
Сумма всех углов треугольника — 180 градусов.
Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.

Видео:САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

Проведем серединные
перпендикуляры — HO, FO, EO.
O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника.
Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Как найти периметр треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Определение

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.

Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Как узнать периметр треугольника

Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.

Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.

P = a + b + c, где a, b, c — длина стороны.

Если известна площадь и радиус вписанной окружности:

P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.

Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:

P = √ b 2 + с 2 — 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.

Если известна одна сторона в равностороннем треугольнике:

P = 3 * a, где a — длина стороны.

Все стороны в равносторонней фигуре равны.

Если известна боковая сторона и основание в равнобедренном треугольнике:

P = 2 * a + b, где a — боковая сторона, b — основание.

Боковые стороны в равнобедренной фигуре равны.

Если известна боковая сторона и высота в равнобедренном треугольнике:

P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.

Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.

Если известны катеты в прямоугольном треугольнике:

P = √ a 2 + b 2 + (a + b), где a, b — катеты.

Катет — одна из двух сторон, которые образуют прямой угол.

Если известны катет и гипотенуза в прямоугольном треугольнике:

P = √ c 2 — a 2 + (a + c), где a — любой катет, c — гипотенуза.

Гипотенуза — сторона, которая лежит напротив прямого угла.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Видео:8 класс, 38 урок, Вписанная окружностьСкачать

Решение геометрических задач на нахождение наибольшего и наименьшего значений с помощью производной

Видео:ЕГЭ Математика Задание 6#27935Скачать

Планиметрические задачи

Задача 1.Написать уравнения касательной и нормали к графику функциив данной точке, если:

Решение. Уравнение касательной будем искать по формуле ; уравнение нормали — по формуле По условию, .

Подставляем все найденные значения в уравнение касательной:

Теперь находим уравнение нормали:

Ответ: уравнение касательной:; уравнение нормали:

Задача 2.Написать уравнения касательной и нормали в точке

Подставим полученные решения в равенство

Найдем производную функции, заданной параметрически .

Подставляем все найденные значение в уравнение касательной:

Теперь находим уравнение нормали:

Ответ: уравнение касательной: уравнение нормали: .

Задача 3. Найти углы, под которыми пересекаются заданные кривые:

Решение. Угол между кривыми находится по формуле

Найдем координаты точки пересечения заданных кривых. Решаем систему уравнений:

Таким образом, кривые пересекаются в точках .

Далее найдем значения производных заданных функций в точках пересечения.

производный дифференцирование уравнение планиметрический

Подставляем найденные значение в формулу нахождения угла:

Ответ: в точке угол равен 0 (т.е. касательные совпадают), в точке угол равен .

Задача 4. Задан прямоугольник с периметром 56 см. Каковы должны быть его стороны, чтобы площадь была наибольшей [7]?

Обозначим одну из сторон за, тогда вторая сторона:

Площадь такого прямоугольника составит:

Требуется найти максимум функции .

Это квадратичная функция, ее график — парабола, ветви которой направлены вниз.

Определим критические точки: .

Так, — точка экстремума, слева от нее производная положительна, а справа — отрицательна.

Очевидно, что — точка максимума. В таком случае площадь прямоугольника максимальна, когда его стороны равны 14 см, то есть когда он является квадратом.

Ответ: площадь максимальна, когда стороны прямоугольника равны 14 см.

Задача 5. Площадь прямоугольника составляет . Каковы должны быть его размеры этого прямоугольника, чтобы периметр был минимальным?[7]

Пусть стороны прямоугольника равны . Тогда:

Периметр такого прямоугольника составит:

Требуется найти минимум данной функции. Найдём производную:

Найдем точки экстремума:

Очевидно, что , поэтому нас интересует точка .Слева от нее производная отрицательна, а справа — положительна.

Так, — точка минимума.

Ответ: чтобы периметр прямоугольника был минимальным, его стороны должны составить 4 см.

Задача 6. Две стороны параллелограмма лежат на сторонах заданного треугольника, а одна из его вершин принадлежит третьей стороне. Найти условия, при которых площадь параллелограмма является наибольшей [2].

Пусть треугольник определяется двумя сторонами и углом между ними (рис.4). Построим параллелограмм в соответствии с условиями задачи. Обозначим стороны параллелограмма Площадь параллелограмма определяется формулой

Выразим через и стороны треугольника . Из подобия треугольников и следует, что

В результате площадь записывается как функция:

Отсюда видно, что экстремум функциисуществует в следующей точке:

При переходе через эту точку производная меняет свой знак с плюса на минус, то есть эта точка является точкой максимума. Другая сторона параллелограмма при этом равна

Итак, вписанный в треугольник параллелограмм со сторонами имеет наибольшую площадь при условии

где стороны треугольника. Интересно, что результат не зависит от угла между сторонами треугольника.

Ответ: площадь параллелограмма является наибольшей при условии

где стороны треугольника.

Задача 7.Среди всех равнобедренных треугольников, вписанных в данную окружность, найти треугольник с наибольшим периметром [2].

Пусть треугольник вписан в окружность данного радиуса ,

(независимая переменная) (рис.5). Выразим периметр треугольника как функцию . По теореме синусов:

. Найдем, при каком значении функция принимает наибольшее значение на данном интервале

следовательно, точка максимума, в которой функция принимает наибольшее значение на заданном промежутке. Таким образом, наибольший периметр имеет равносторонний треугольник.

Ответ: среди всех равнобедренных треугольник, вписанных в данную окружность, с наибольшим периметром является равносторонний треугольник.