Докажите что треугольник mpk равнобедренный

Вопрос по алгебре:

Прямые AB и MP параллельны. По данным рисунка докажите, что треугольник MPK равнобедренный

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Угол ABK равен углу MPK, как соответственные углы при параллельных прямых AB и MP и секущей BK. Угол ABK равен углу BKA по условию. Следовательно, угол MPK равен углу PKM (что тоже самое, что угол BKA), и треугольник MPK является равнобедренным с боковыми сторонами MP и MK и основанием KP по признаку равнобедренного треугольника.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.

Видео:№947. Докажите, что треугольник ABC равнобедренный, и найдите его площадь, если вершины треугольникаСкачать

Докажите что треугольник mpk равнобедренный

Из этой теоремы следует, что в треугольнике против равных углов лежат равные стороны .

Если медиана треугольника является его биссектрисой, то этот треугольник равнобедренный.

Рассмотрим треугольник ABC , у которого отрезок BM — медиана и биссектриса. Надо доказать, что AB = BC .

На луче BM отложим отрезок MD , равный отрезку BM (рис. 171).

В треугольниках AMD и CMB имеем: AM = MC (так как по условию BM — медиана), BM = MD по построению, углы AMD и CMB равны как вертикальные. Следовательно, треугольники AMD и CMB равны по первому признаку равенства треугольников.

Тогда стороны AD и BC , углы ADM и CBM равны как соответственные элементы равных треугольников.

Так как BD — биссектриса угла ABC , то ∠ ABM = ∠ CBM . Поскольку ∠ CBM = ∠ ADM , то получаем, что ∠ ABM = ∠ ADM .

Тогда по теореме 10.3 получаем, что треугольник DAB — равнобедренный, откуда AD = AB . И уже доказано, что AD = BC . Следовательно, AB = BC .

Задача. В треугольнике ABC проведена биссектриса BM (рис. 172), ∠ BAK = 70°, ∠ AKC = 110°. Докажите, что BM ⊥ AK .

Решение. Так как углы BKA и AKC — смежные, то ∠ BKA = 180° — ∠ AKC . Тогда ∠ BKA = 180° — 110° = 70°.

Следовательно, в треугольнике ABK получаем, что ∠ BAK = ∠ BKA = 70°. Треугольник ABK — равнобедренный с основанием AK , и его биссектриса BO ( O — точка пересечения AK и BM ) является также высотой, т. е. BM ⊥ AK .

1. Сформулируйте признаки равнобедренного треугольника.
2. Какова связь между равными углами и равными сторонами треугольника?

232. В треугольнике ABC медиана BK перпендикулярна стороне AC . Найдите ∠ ABC , если ∠ ABK = 25°.

233. Серединный перпендикуляр стороны AC треугольника ABC проходит через вершину B . Найдите ∠ C , если ∠ A = 17°.

234. В треугольнике ABC известно, что ∠ ACB = 90°, ∠ A = ∠ B = 45°, CK — высота. Найдите сторону AB , если CK = 7 см.

235. На рисунке 173 ∠ AMK = ∠ ACB , AK = MK . Докажите, что ∆ ABC — равнобедренный.

236. Прямая, перпендикулярная биссектрисе угла A , пересекает его стороны в точках B и C . Докажите, что ∆ ABC — равнобедренный.

237. Биссектрисы AM и CK углов при основании AC равнобедренного треугольника ABC пересекаются в точке O . Докажите, что ∆ AOC — равнобедренный.

238. В треугольнике ABC биссектриса BK является его высотой. Найдите периметр треугольника ABC , если периметр треугольника ABK равен 16 см и BK = 5 см.

239. Верно ли утверждение:

1) если медиана и высота треугольника, проведённые из одной вершины, не совпадают, то этот треугольник не является равнобедренным;

2) если биссектриса треугольника делит противолежащую сторону пополам, то этот треугольник равнобедренный?

240. Медианы AE и CF , проведённые к боковым сторонам BC и AB равнобедренного треугольника ABC , пересекаются в точке M . Докажите, что треугольник AMC — равнобедренный.

241. Точки M и K принадлежат соответственно боковым сторонам AB и BC равнобедренного треугольника ABC , AM = CK . Отрезки AK и CM пересекаются в точке O . Докажите, что ∆ AOC — равнобедренный.

242. На сторонах AB и BC треугольника ABC отметили соответственно точки D и E так, что ∠ EAC = ∠ DCA . Отрезки AE и CD пересекаются в точке F , DF = EF . Докажите, что ∆ ABC — равнобедренный.

243. Через середину D стороны AB треугольника ABC проведены прямые, перпендикулярные биссектрисам углов ABC и BAC . Эти прямые пересекают стороны AC и BC в точках M и K соответственно. Докажите, что AM = BK .

244. Медиана AM треугольника ABC перпендикулярна его биссектрисе BK . Найдите сторону AB , если BC = 16 см.

245. Прямая, проходящая через вершину A треугольника ABC перпендикулярно его медиане BD , делит эту медиану пополам. Найдите отношение длин сторон AB и AC треугольника ABC .

246. В треугольнике ABC известно, что ∠ C = 90°, ∠ A = 67,5°, ∠ B = 22,5°, CK — биссектриса треугольника ABC , CM — биссектриса треугольника BCK (рис. 174). Докажите, что точка M — середина отрезка AB .

247. Длины сторон треугольника, выраженные в сантиметрах, равны трём идущим подряд натуральным числам. Найдите стороны этого треугольника, если одна из его медиан перпендикулярна одной из его биссектрис.

248. В треугольнике ABC известно, что AB = 3 см, BC = 4 см, AC = 6 см. На стороне BC отметили точку M такую, что CM = 1 см. Прямая, проходящая через точку M перпендикулярно биссектрисе угла ACB , пересекает отрезок AC в точке K , а прямая, проходящая через точку K перпендикулярно биссектрисе угла BAC , пересекает прямую AB в точке D . Найдите длину отрезка BD .

Упражнения для повторения

249. На прямой последовательно отметили точки A , B , C , D , E и F так, что AB = BC = CD = DE = EF . Найдите отношения AB : CF , AB : BF , BD : AE .

250. Найдите углы, образованные при пересечении двух прямых, если один из них на 42° больше половины второго угла.

Наблюдайте, рисуйте, конструируйте, фантазируйте

251. Разрежьте прямоугольник размером 4 × 9 на две равные части, из которых можно сложить квадрат.

Видео:№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать

Докажите , что треугольник KMN равнобедренный , если KP = TN , угол MPT = углу MTP?

Геометрия | 10 — 11 классы

Докажите , что треугольник KMN равнобедренный , если KP = TN , угол MPT = углу MTP.

Iz treugolnika PMT

ugol MPT = ugol MTP , sleduet, chto PM = MT

ugol KPM = 180 — ugolMPT

ugol MTN = 180 — ogol MTP, poskolku ugol MPT = ugol MTP, sleduet ugol KPM = ugol MTN

sleduet treugolnik KMP = treugolnik MTN (MP = MT, KP = TN, ugol MPK = ugol MTN)

Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

В равных треугольниках DEA и FEB : угол D = углу F?

В равных треугольниках DEA и FEB : угол D = углу F.

Докажите , что треугольник АЕВ — равнобедренный.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

В треугольнике АВС угол, смежный с углом А, равен 150 градусам, а угол, вертикальный с углом С, равен 30 градусам?

В треугольнике АВС угол, смежный с углом А, равен 150 градусам, а угол, вертикальный с углом С, равен 30 градусам.

Докажите , что треугольник АВС — равнобедренный.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

В треугольнике KMN угол К = углу N?

В треугольнике KMN угол К = углу N.

На высоте MH отмечена точка D.

Докажите, что треугольник KDN — равнобедренный.

Видео:Равнобедренный треугольник. 7 класс.Скачать

Доказать, что если в треугольнике KMN медиана МА перпендикулярна стороне KN, то треугольник KMN — равнобедренный?

Доказать, что если в треугольнике KMN медиана МА перпендикулярна стороне KN, то треугольник KMN — равнобедренный.

Видео:Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

В равных треугольниках DEA и FEB угол D равен углу F, Докажите что треугольник AEB равнобедренный?

В равных треугольниках DEA и FEB угол D равен углу F, Докажите что треугольник AEB равнобедренный.

Видео:№111. На рисунке 65 CD = BD, ∠1=∠2. Докажите, что треугольник ABC равнобедренный.Скачать

Докажите, что треугольник MOK равнобедренный, если известно, что угол 1 равен углу 2?

Докажите, что треугольник MOK равнобедренный, если известно, что угол 1 равен углу 2.

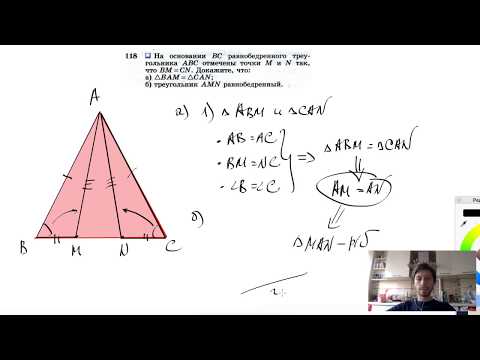
Видео:№118. На основании ВС равнобедренного треугольника ABC отмечены точки М и N так, что BM=CN. ДокажитеСкачать

В треугольнике KMN, угол К = углу N?

В треугольнике KMN, угол К = углу N.

На высоте МН отмечена точка D.

Докажите, что треугольник KDN — равнобедреный.

Видео:Свойства равнобедренного треугольника. 7 класс.Скачать

В равнобедренном треугольнике АВС биссектрисы равных углов В и С пересекаются в точке О?

В равнобедренном треугольнике АВС биссектрисы равных углов В и С пересекаются в точке О.

Докажите, что угол ВОС равен внешнему углу треугольника при вершине В.

Видео:Равнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать

На рисунке CD = BD, угол 1 = углу 2?

На рисунке CD = BD, угол 1 = углу 2.

Докажите что треугольник ABC равнобедренный.

Видео:№133. Докажите, что если биссектриса треугольника совпадает с его высотой, то треугольникСкачать

Докажите теорему (признак равнобедренного треугольника) : если два угла треугольника равны, то этот треугольник равнобедренный?

Докажите теорему (признак равнобедренного треугольника) : если два угла треугольника равны, то этот треугольник равнобедренный.

На этой странице сайта вы найдете ответы на вопрос Докажите , что треугольник KMN равнобедренный , если KP = TN , угол MPT = углу MTP?, относящийся к категории Геометрия. Сложность вопроса соответствует базовым знаниям учеников 10 — 11 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

И так рассмотрим треугольник АВЕ — равнобедренный ВЕ = ВF тогда P = (BF * 6 + 4BF) = 10BF = 88 AB = 2BF = 88 5.

По условию периметр АВСD = R + R + R + 2R = 5R / 60. R = 60 / 5 = 12 см. АD = 2R = 12·2 = 24 см. См. фото.

Отрезки диагоналей в параллелограмме попарно равны, поэтому AO = CO = 12см, а DO = BO = 9 см. Тогда Paob = AO + BO + AB = 12 + 9 + 15 = 21 + 15 = 36 см Ответ : 36 см.

Доказать равенство треугольников ВМА и КСД : углы ВАМ и КСД расвны по условию, стороны АВ = СД как стороны параллелограмма, углы АВМ и КДС равны на внутренние накреслежащие припараллельных ВС и АД.

Vкуба = a³a³ = 3000√3a = ∛(3000√3) = 10∛(3√3) = 10∛(√27) = 10√3Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. А для квадрата : d² = 3a² = 3 · 300 = 900d = 30.

BD = 36 * 2 = 72 т. К в прямоугольном треугольнике катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы.

При пересечении двух прямых образуется 4 угла и их сумма равна 360°. Если сумма трёх из них равна 306° , то градусная мера четвёртого угла равна 360 — 306 = 54°. Смежный с ним угол равен 180 — 54 = 126° — это и есть больший из них.

Дано : Решение : АО = 21 см Т. К. по условию задачи CD = 56 см отрезки АВ и CD P = 83 см разделены т. О пополам, Найти : то СО = 56 / 2 = 28 BD — ? Рассмотрим треугольники АОС и ОBD : 1) AO = OB по условию ; 2)CO = OD по условию ; 3)угол AOC = уго..

38 см 5 мм вот вроде так.

1. Была какая — то теорема для быстрого решения подобной задачи, но я ее не помню, так что так Рассмотрим треугольники МКО и МНО угол ОМК = углу ОМН по условию МК — общая НОМ = 180 — (ОНМ = НМО), КОМ = 180 — (ОКМ — КМО), тк ОКМ = ОНМ = > НОМ = КОМ Из..

🌟 Видео

Признаки равенства треугольников. 7 класс.Скачать

Равнобедренный треугольник. Практическая часть. 7 класс.Скачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Две задачи по геометрии за 7 класс на тему: "Треугольники"Скачать

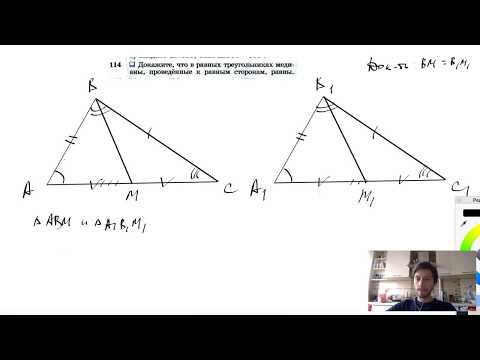
№114. Докажите, что в равных треугольниках медианы, проведенные к равным сторонам, равны.Скачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

Геометрия. 7 класс. Теоремы. Т6. Второе свойство равнобедренного треугольника.Скачать