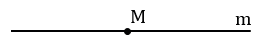Построение перпендикуляра двумя окружностями (5 видео)

Построение перпендикулярных прямых

Примеры:

1. Даны прямая и точка на ней. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.

Дано: прямая m, M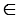m.

Построить: МPm.

Решение:

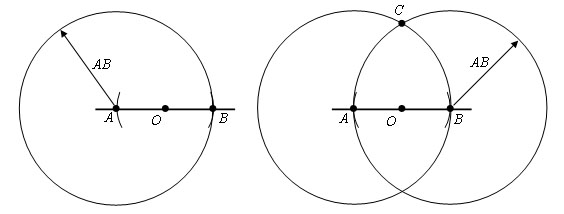
Произвольно строим с помощью линейки прямую m и отмечаем на ней точку М.

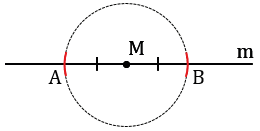
На лучах прямой m, исходящих из точки М, с помощью циркуля откладываем равные отрезки МА и МВ (МА = МВ). Для этого строим окружность с центром в точке М, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки М (смотри выделенное красным).

Затем строим две окружности с центрами в точках А и В радиуса АВ (полностью окружности строить необязательно, смотри выделенное фиолетовым и красным цветом).

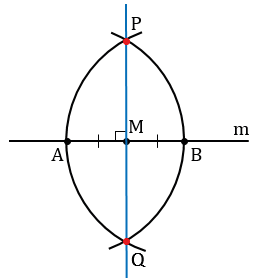
Данные окружности пересекаются в двух точках, обозначим их Р и Q. Проведем с помощью линейки через точку М и одну из точек Р или Q прямую, например, МР.

Докажем, что прямая МР — искомая прямая, т.е. что МPm.

Рассмотрим треугольник АРВ.

АР = ВР, т.к. по построению это радиусы одинаковых окружностей, следовательно, АРВ — равнобедренный. По построению МА = МВ, т.е. МР — медиана равнобедренного треугольника, тогда по свойству равнобедренного треугольника МР и высота, т.е. МPm. Что и требовалось доказать.

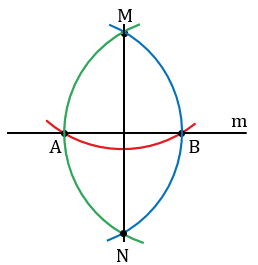
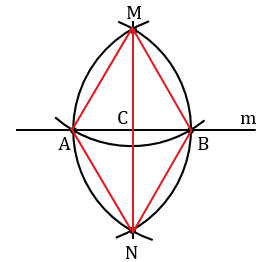
2. Даны прямая и точка не лежащая на этой прямой. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.

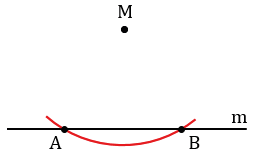
Дано: прямая m, Mm.

Построить: МNm.

Решение:

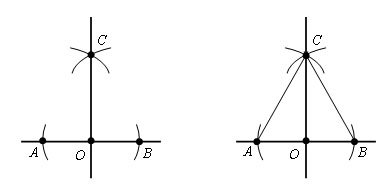
Произвольно строим с помощью линейки прямую m и отмечаем точку М, не лежащую на прямой m.

Далее строим окружность с центром в данной точке М, пересекающую прямую m в двух точках, которые обозначим буквами А и В (всю окружность строить необязательно, смотри выделенное красным цветом).

Затем построим две окружности с центрами в точках А и В, проходящие через точку М (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Эти окружности пересекутся в точке М и еще в одной точке, которую обозначим буквой N. Проведем прямую МN.

Докажем что, прямая МN — искомая, т.е. МNm.

В АМN и ВМN: АМ = АN = ВМ = ВN — радиусы, МN — общая, следовательно, АМN =ВМN (по трем сторонам), значит, углы ВМС и АМС равны (С точка пересечения прямых m и МN). Отсюда следует, что отрезок МС — биссектриса равнобедренного треугольника АМВ (АМ = ВМ — радиусы) с основанием АВ, тогда по свойству равнобедренного треугольника АМ — высота, значит, МNАВ, т.е. МNm.

Поделись с друзьями в социальных сетях:

Содержание

Построение перпендикуляра к линии
Построение перпендикуляра из данной точки к прямой
Построение перпендикуляра из данной точки к кривой линии
Построение перпендикуляра двумя окружностями
🎬 Видео

Видео:1 2 4 сопряжение окружностейСкачать

Построение перпендикуляра к линии

Видео:Перпендикуляр к прямой через заданную точку.Скачать

Построение перпендикуляра из данной точки к прямой

Из данной точки С проводят дугу окружности произвольного радиуса так чтобы она пересекала прямую, заданную отрезком АВ, в точках D и F. Из этих точек описывают две дуги окружности радиусом R, несколько большим половины отрезка DF, до пересечения в точке Е. Точки С и Е соединяют прямой которая и будет искомым перпендикуляром.

Видео:Построение перпендикуляра к прямойСкачать

Построение перпендикуляра из данной точки к кривой линии

Построение нормали к кривой проходящей через точку А, не принадлежащую кривой m, можно выполнить следующим образом:

2. Отметим точки пересечения окружностей с кривой -1, 1₁, 2, 2₁, 3, 3₁, 4, 4₁;

3. Из концов хорд восстановим перпендикуляры (при этом перпендикуляры, восстановленные из точек 1, 2, 3, 4, имеют противоположное направление перпендикулярам, восстановленным из точек 1₁, 2₁, 3₁, 4₁);

4. На полученных перпендикулярах отложим отрезки, равные длине соответствующих хорд;

5. Полученные точки соединим плавной кривой l;

Видео:Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Построение перпендикуляра двумя окружностями

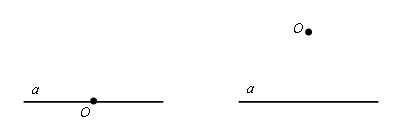
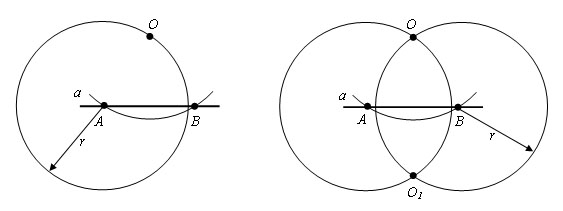
Через точку O провести прямую, перпендикулярную данной прямой a.

Возможно два варианта:

точка O лежит на прямой a;
точка О не лежит на прямой a.

Рассмотрим поочередно оба варианта.

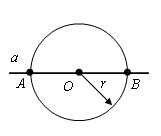
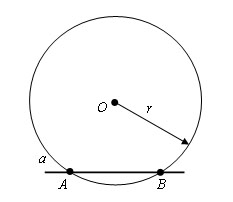
Шаг 1. Проводим окружность с произвольным радиусом r с центром в точке O. Окружность пересекает прямую в точках A и B.

Шаг 2. Из точек A и B проводим окружности с радиусом AB. Пусть тоска С – точка пересечения этих окружностей.

Обращаю ваше внимание на то что точки А и В мы получили на первом шаге, при построении окружности с произвольным радиусом.

Шаг 3. Искомая прямая проходит через точки С и О.

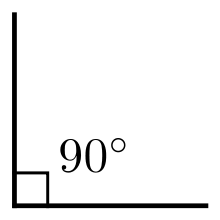
Проведем отрезки AC и CB. Δ ACO = Δ BCO по третьему признаку равенства треугольников (AO = OB, AC = CB, по построению, CO – общая). ∠ COA = ∠ COB = 90 °. Прямая CO ⊥ AB.

Как было уже сказано выше все четыре угла образованных при пересечении двух прямых перпендикулярны если хотя бы один из них перпендикулярен, т.е. является прямым и равен 90 градусов.

Второй вариант такой же простой только имеет немного другой принцип поиска наших начальных точек А и В.

Шаг 1. Из точки O проводим окружность некоторым радиусом r, таким чтобы окружность пересекала прямую a. Пусть A и B – точки пересечения окружности с прямой a.

Шаг 2. Проведем окружности тем же радиусом r с центрами в точках A и B. Пусть точка O₁ – точка пресечения этих окружностей, лежащая в полуплоскости, отличной от той, в которой лежит точка O.

Шаг 3. Проведем через точки O и O₁ прямую. Это и будет искомая прямая.

Пусть прямые OO₁ и AB пересекаются в точке С. Δ AOB = Δ BO₁A по третьему признаку равенства треугольников (AO = OB = AO₁ = O₁B, по построению, AB – общая). Отсюда следует, что ∠ OAС = ∠ O₁AC. Δ OAC = Δ O₁AC по первому признаку равенства треугольников (AO = AO₁, по построению, ∠ OAС = ∠ O₁AC, AС – общая). Следовательно ∠ OСA = ∠ O₁CA, а так как эти углы смежные, то они прямые. Поэтому OC – перпендикуляр, опущенный из точки O на прямую a.

Т. е. с помощью циркуля и линейки мы можем стоить перпендикулярные прямые, независимо от того точка через какую должен проходить перпендикуляр находиться на отрезке или за его пределами. Оба варианта имеют три шага, единственная сложность в том что бы правильно найти начальные точки А и В.