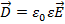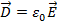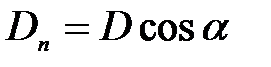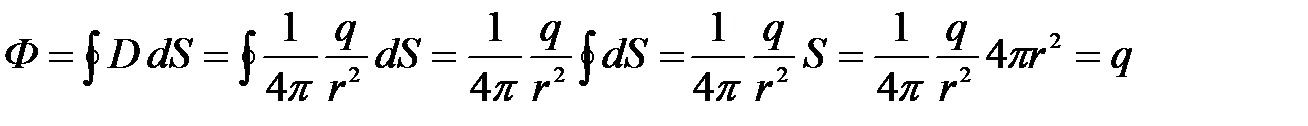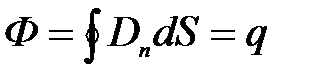Читайте также:
|
Напряженность электростатического поля зависит от свойств среды (ε). Кроме того, вектор напряженности 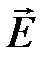
Изотропи́я, изотро́пность (из др.-греч. «равный, одинаковый, подобный» + «оборот, поворот; характер») — одинаковость физических свойств во всех направлениях, инвариантность, симметрия по отношению к выбору направления (в противоположность анизотропии).
Единица электрического смещения — Кл/м 2 .
для вакуума:
это силовая характеристика поля в вакууме.
Если есть однородное поле со смещением D, то потоком электрического смещения называется величина:
где a – угол между нормалью к площадке S и направлением D (рис.7).
Если поле неоднородно (рис.8), то можно выбрать малую площадку dS, в рамках которой поле можно считать однородным. Поток через нее:
Рассчитать поток электрического смещения через любую поверхность можно по формуле: 
где 
Поток вектора напряженности электрического поля определяется как: 
Теорема Гаусса позволяет определить поток вектора смещения (или напряженности) электростатического поля, создаваемого системой зарядов. Определим поток электрического смещения сквозь сферическую поверхность радиусом r, в центре которой расположен точечный заряд +q. По формуле для потока имеем 
Для точечного заряда 
Линии электрического смещения перпендикулярны поверхности сферы, a=0; следовательно, cos a = 1. Тогда 
Теорему Гаусса можно записать в виде:
Если поле создается несколькими зарядами, то 
Теорема Гаусса: поток вектора электрического смещения через любую замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности.
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)
Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Поток вектора электрического смещения через поверхность сферы
отсюда можно записать:
где P = . — вектор поляризации; . — диэлектрическая восприимчивость среды, характеризующая поляризацию единичного объема среды.
Таким образом, вектор D есть сумма (линейная комбинация) двух векторов различной природы: E — главной характеристики поля и P — поляризации среды.
В СИ . т.е. это заряд, протекающий через единицу поверхности.
Для точечного заряда в вакууме .
Для D имеет место принцип суперпозиции, как и для E , т.е.
1.4.4. Поток вектора электрического смещения. Теорема Остроградского-Гаусса для D
Аналогично потоку для вектора E . можно ввести понятие потока для вектора D (ΦD). Пусть произвольную площадку S пересекают линии вектора электрического смещения D под углом α к нормали n (рис. 1.4.10):
В однородном электростатическом поле ΦD = DS cos α = DnS.
Теорему Остроградского — Гаусса для вектора D получим из теоремы Остроградского — Гаусса для вектора E:
Видео:45. Электрическое смещениеСкачать

Поток вектора электрического смещения.
Теорема Остроградского — faycca для D
Аналогично потоку для вектора можно ввести
понятие «поток вектора электрического смещения» Ь(ФD). Пусть произвольную площадку S пересекают линии вектора электрического смещения D под углом а к нормали п (рис. 1.4.10):
В однородном электростатическом поле Ф0 = DScosa = DnS. Теорему Остроградского — Гаусса для вектора D получим из теоремы Остроградского — Гаусса для вектора Е:
так как 
Теорему Остроградского — Гаусса для D можно записать в следующем виде:
Поток вектора D через любую замкнутую поверхность определяют только свободные заряды, а не все заряды внутри объема, ограниченного данной поверхностью. Это позволяет не рассматривать связанные (поляризованные) заряды, влияющие на Ё,_и упрощает решение многих задач. В этом смысл введения вектора D.
Видео:Урок 223. Теорема ГауссаСкачать

Изменение Ё и D на границе раздела двух диэлектриков
Рассмотрим простой случай (рис. 1.4.11): два бесконечно протяженных диэлектрика се, и е2, имеющих общую границу раздела, пронизывает внешнее электростатическое поле Ё0. Пусть е2 > е,. Из п. 1.4.3следует,что Е<п/Е2п=г2/г1 и Еи = Е2х.
Образовавшиеся поверхностные заряды изменяют только нормальную составляющую Ё, а тангенциальная составляющая остается постоянной (см. рис. 1.4.11):
т.е. направление вектора Ё изменяется. Это закон преломления вектора напряженности электростатического поля.

Рис. 1.4.11 Рис. 1.4.12
Изменение вектора D и его проекций — Dn и Dx приведены на рис. 1.4.11. _
Так как D = гпгЁ, то
нормальная составляющая вектора D, не изменяется);

вектора D увеличивается в е2/е, раз).
Следовательно, закон преломления вектора D имеет следующий вид:
Закон преломления для векторов Ё и D показан на рис. 1.4.13. Как видно из рис. 1.4.13 , при переходе из одной диэлектрической среды в другую вектор D преломляется на тот же угол, что и Ё(5 = ег0Ё). Входя в диэлектрик с большей диэлектрической проницаемостью, линии D и Ё удаляются от нормали.
Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

КОНТРОЛЬНЫЕ ВОПРОСЫ. УПРАЖНЕНИЯ
- 1. Указать виды поляризации.
- 2. Что показывает диэлектрическая проницаемость среды?
- 3. Вывести связь между диэлектрической восприимчивостью вещества и проницаемостью среды.
- 4. В чем различие поляризации диэлектриков с полярными и неполярными молекулами?
- 5. Есть ли свободные заряды в идеальном диэлектрике?
- 6. Какие виды поляризуемости существуют?
- 7. Назвать три основных класса веществ в соответствии с их способностью проводить электрический ток.
- 8. Определить, где диэлектрическая проницаемость при построении рис. 1 больше, меньше.
- 9. Что представляет собой вектор электрического смещения?
- 10. Сформулировать теорему Остроградского — Гаусса для электростатического поля в диэлектрике.
- 11. Вывести и прокомментировать условия для векторов ? и D на границе раздела двух диэлектрических сред.
- 12. Сформулируйте закон преломления для векторов Ё л D.
📹 Видео
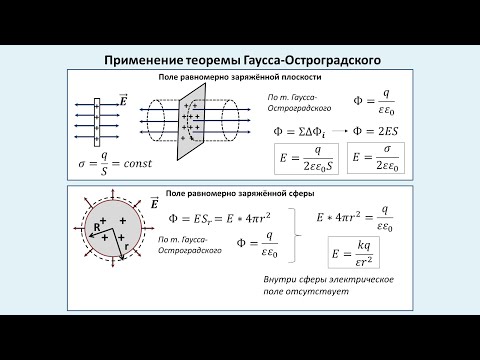
Применение теоремы Гаусса-Остроградского. Напряжённость поля пластины, сферы и шара.Скачать
Урок 222. Поток вектора напряженности электрического поляСкачать

Билет №02 "Теорема Гаусса"Скачать

Теорема Гаусса. Поле заряженной сферы. Электростатика.Скачать

43. Применение теоремы ГауссаСкачать

Задача №2. Потенциал проводящей сферы.Скачать

Урок 224. Напряженность поля неточечных зарядовСкачать

Физика. 10 класс. Поток вектора напряженности электрического поля. Теорема Гаусса /18.01.2021/Скачать

Урок 225. Задачи на поток вектора напряженности электрического поляСкачать

Электростатика. Теорема Остроградского - ГауссаСкачать

ЭЛЕКТРОСТАТИКА.Задачи на применение теоремы Гаусса. 2022-2Скачать

Поток через замкнутую поверхность. Формула Остроградского-ГауссаСкачать

Электростатика | поток напряженности электрического поляСкачать
Потенциал сферы и проводящего шараСкачать

42. Теорема Гаусса. Расчет электростатических полейСкачать

Поток вектора напряженности электрического поля. Теорема Гаусса. Практическая часть. 10 класс.Скачать