Конспект урока
Геометрия, 10 класс
Урок №6. Параллельность плоскостей
Перечень вопросов, рассматриваемых в теме
- Определение параллельных плоскостей;
- Свойства параллельных плоскостей;
- Признак параллельности плоскостей.
Глоссарий по теме
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Определение. Плоскости, которые не пересекаются, называются параллельными.
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии 10 Москва «Просвещение» 2013 год. С. 1-4.
Зив Б. Г. Геометрия 10 класс Дидактические материалы Москва «Просвещение» 2013 год. С.4, 14, 24
Теоретический материал для самостоятельного изучения
Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит две плоскости или пересекаются, или не пересекаются.
Определение. Плоскости, которые не пересекаются, называются параллельными.
Параллельные плоскости α и β обозначаются α∥β.
Любая конструкция с полом, потолком и стенами даёт нам представление о параллельных плоскостях — пол и потолок как две параллельные плоскости, боковые стены как параллельные плоскости.

Пусть α и β — данные плоскости, a1 и a2 – пересекающиеся прямые в плоскости α, а b1 и b2 соответственно параллельные им прямые в плоскости β.
Допустим, что плоскости α и β не параллельны, то есть они пересекаются по некоторой прямой c.
Прямая a1 параллельна прямой b1, значит она параллельна и самой плоскости β.
Прямая a2 параллельна прямой b2, значит она параллельна и самой плоскости β (признак параллельности прямой и плоскости).
Прямая c принадлежит плоскости α, значит хотя бы одна из прямых a1 или a2 пересекает прямую c, то есть имеет с ней общую точку. Но прямая c также принадлежит и плоскости β, значит, пересекая прямую c, прямая a1 или a2 пересекает плоскость β, чего быть не может, так как прямые a1 и a2 параллельны плоскости β.
Из этого следует, что плоскости α и β не пересекаются, то есть они параллельны.
Свойства параллельных плоскостей.

Пусть α и β — параллельные плоскости, а γ- плоскость, пересекающая их.
Плоскость α пересекается с плоскостью γ по прямой a.
Плоскость β пересекается с плоскостью γ по прямой b.
Линии пересечения a и b лежат в одной плоскости γ и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.

Пусть α и β — параллельные плоскости, а a и b – параллельные прямые, пересекающие их.
Через прямые a и b можно провести плоскость — эти прямые параллельны, значит определяют плоскость, причём только одну.
Проведённая плоскость пересекается с плоскостью α по прямой AB, а с плоскостью β по прямой CD.
По предыдущей теореме прямые AB и CD параллельны. Четырехугольник ABCD есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть BC=AD.
Теорема 3. Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.
Пусть α||β, a пересекает α в точке А.
Выберем в плоскости любую точку C. Через эту точку и прямую a проведём плоскость.
Так как плоскость имеет с плоскостями α и β общие точки A и C соответственно, то она пересекает эти плоскости по некоторым прямым b и c, которые проходят соответственно через точки A и C. По предыдущей теореме прямые b и c параллельны. Тогда в плоскости прямая a пересекает (в точке A) прямую b, которая параллельна прямой c. Значит, прямая a пересекает и прямую c в некоторой точке B. Так как прямая c лежит в плоскости, то точка B является точкой пересечения прямой a и плоскости. Теорема доказана.

Пусть α||β, α и γ пересекаются.
Докажем, что плоскости β и γ пересекаются.
Проведём в плоскости γ прямую a, пересекающую плоскость α в некоторой точке B. Тогда по теореме 3 прямая a пересекает и плоскость β в некоторой точке A. Следовательно, плоскости β и γ имеют общую точку A, т. е. пересекаются. Теорема доказана.
Теорема 5. Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.
Пусть нам даны плоскость α и точка М, ей не принадлежащая.
Докажем, что существует плоскость β, которой принадлежит точка М, параллельная плоскости α.

Докажем методом от противного, что β — единственная плоскость, удовлетворяющая условию теоремы.
Допустим, что через точку M проходит другая плоскость, например β1, параллельная α.
Так как β1 пересекает плоскость β (они имеют общую точку M), то по теореме 4 плоскость β1 пересекает и плоскость α (β ‖ α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку M можно провести плоскость, отличную от плоскости β и параллельную плоскости α, неверно. Значит, плоскость β — единственна. Теорема доказана.
Рассмотрим несколько примеров на применение данных свойств.
Даны две пересекающиеся прямые a и b точка А, не лежащая в плоскости этих прямых. Докажите, что через точку А проходит плоскость, параллельная прямым a и b, и притом только одна.
Прямые a и b пересекаются по условию, следовательно, по следствию из аксиомы А1, эти прямые единственным образом определяют плоскость α.
Известно, что через точку А, не принадлежащую плоскости α, проходит единственная плоскость, параллельная α, т.е. параллельная прямым a и b (по теореме 5) .
Плоскости α и β параллельны, прямая m лежит в плоскости α. Докажите, что прямая m параллельна плоскости β.
Предположим, что прямая m пересекает плоскость β в точке М. Тогда точка М принадлежит плоскости α (т.к. прямая m лежит в плоскости α) и М принадлежит плоскости β, значит, α и β пересекаются, но они параллельны по условию. Очевидно, m не пересекает плоскость α, т.е. параллельна ей.
Примеры и разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Рассмотрим плоскость, проходящую через прямые А1А2 и В1В2
(она существует и единственная, т.к. прямые пересекаются).
В этой плоскости лежит четырехугольник А1В1А2В2, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А1В1 и А2В2 параллельны.
Аналогично доказывается параллельность В1С1 и В2С2. Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
Рассмотрим плоскость, проходящую через прямые А1А2 и В1В2
(она существует и единственная, т.к. прямые пересекаются).
В этой плоскости лежит четырехугольник А1В1А2В2, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А1В1 и А2В2 параллельны.
Аналогично доказывается параллельность В1С1 и В2С2. Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
Тип задания: выделение цветом
Два равнобедренных треугольника FKС и FKD с общим основанием FK расположены так, что точка С не лежит в плоскости FKD. Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам KС и KD.
Прямые, которые содержат медианы треугольников к KC и KD- выходят из одной точки F. Соответственно, можно сделать вывод, что данные прямые пересекаются.
Видео:Параллельность прямой и плоскости. 10 класс.Скачать

96. Докажите, что отрезки параллельных прямых, заключенные между плоскостью и параллельной ей прямой, равны.
Соединим точки А и В.
А, В, С, D лежат в одной плоскости, что следует из факта m || n. AB || CD (по известной теореме).
Рассмотрим 4-угольник ABCD:
AC || DB — по условию;
AB || CD — по доказанному;
По свойству параллелограмма АС = DB (как противолежащие стороны).

задача №96
к главе «Дополнительные задачи к главе I Параллельность прямых и плоскостей.».
Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Урок «Свойства параллельных плоскостей»
Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
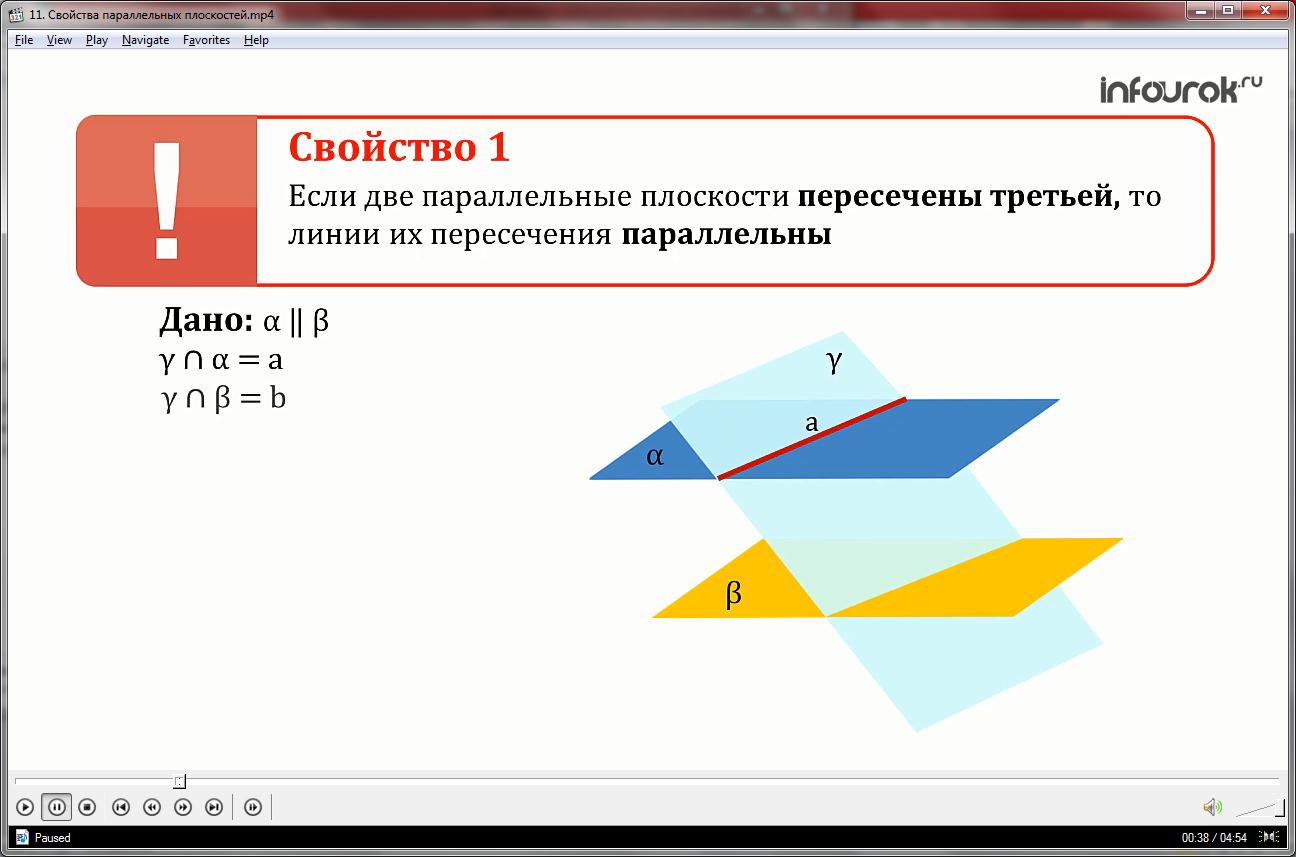
Свойство 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Рассмотрим плоскость и параллельную ей плоскость бэта и плоскость , которая пересекает плоскости по прямой а и плоскость по прямым b
Докажем, что прямые a и b параллельны.
Предположим , что прямые пересекаются, значит они имеют общую точку, которая является общей точкой плоскостей и , что невозможно, так как плоскости по условию параллельны. Значит наше предположение неверно и прямые параллельны.
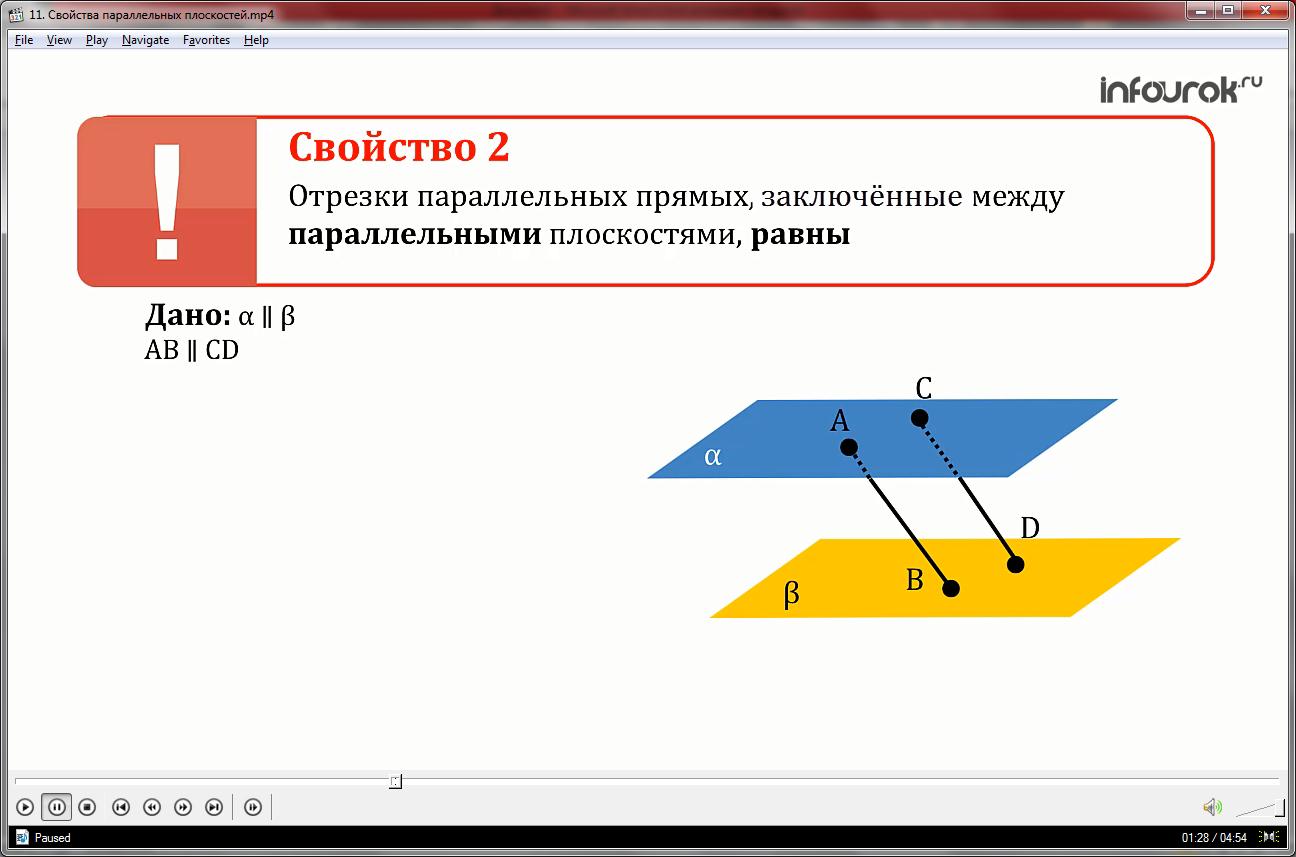
Рассмотрим второе свойство параллельных плоскостей. Свойство 2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Рассмотрим плоскость и параллельную ей плоскость , а также параллельные прямые АВ и СD, которые пересекают эти плоскости.
Докажем, что отрезки АВ и СD, заключенные между параллельными плоскостями, равны.
Две параллельные прямые АВ и СD образуют единственную плоскость γ.
γ пересекает плоскость α по прямой АС, а плоскость β по прямой BD. Так как плоскости α и β по условию паралллеьны, то по доказанному свойству 1 прямые АС и BD паралллеьны.
Рассмотрим четырехугольник ABDC. В нём сторона АС паралельна стороне BD, сторона AB паралельна стороне CD, а четыреугольник у которого строны попарно паралллеьны называется параллелограммом.
По свойству паралллелграмма противоположные стороны AB и CD равны. Что и требовалось доказать.
Рассмотрим применение изученных свойств при решении задач.
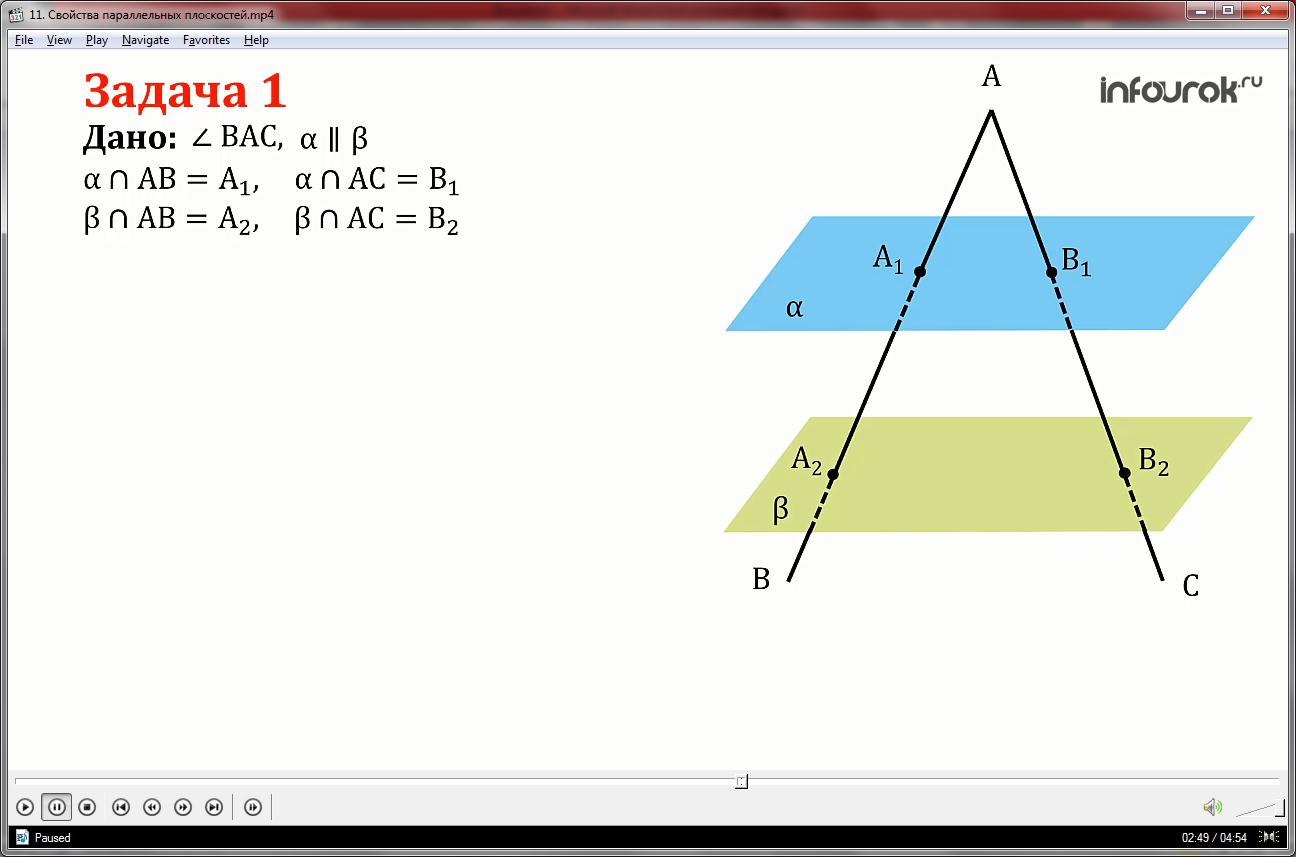
Дан угол ВАС, плоскость α пересекает стороны угла в точках А1 и B1 соответственно, параллельная ей плоскость β пересекает стороны угла ВАС в точках А2 и В2 соответственно. Известно, что отрезок А1А2 равен 12 сантиметрам и в два раза больше отрезка АА1. Отрезок АВ1 равен 5 см.
Найти отрезки АА2 и АВ2
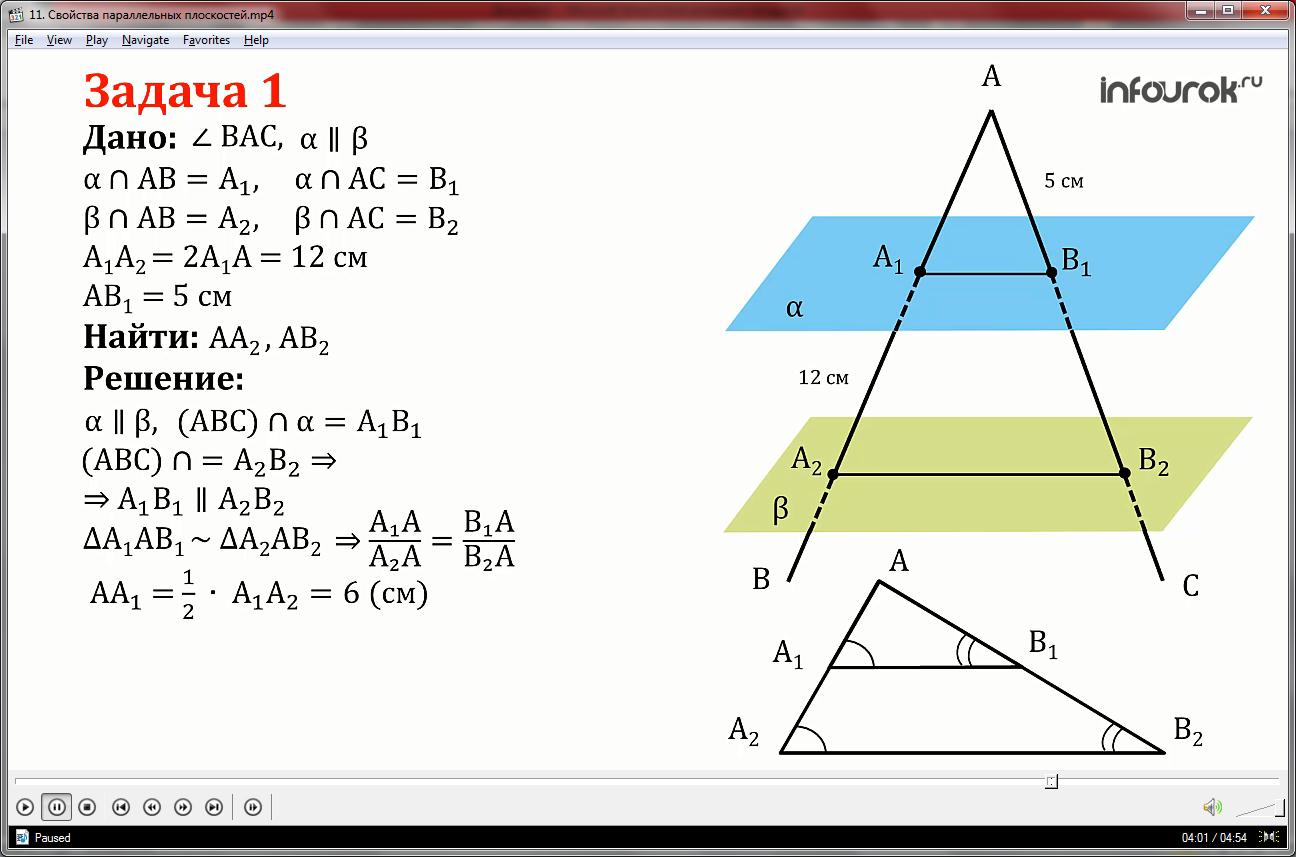
Так как плоскости параллельны по условию и плоскость треугольника АВС, образованная углом ВАС, пересекает их по прямым и , то по свойству параллельных плоскостей прямая .
Рассмотрим плоскость ВАС на отдельном чертеже.
Треугольник А1АВ1 подобен треугольнику А2АВ2 по двум углам. Значит стороны этих треугольников пропорциональны : сторона А1А относится к стороне А2А также как сторона В1А к стороне В2А.
Известно , что АА1 составляет половину стороны А2А1, значит она равна 6 см.
Сторона АА2 равна сумме длин отрезков АА1 и А1А2 и равен 18 сантиметрам.
Подставим найденные значения в пропорцию. Тогда отрезок
Получим ответ: отрезок АА2 равен 18 см, а отрезок АВ2 равен 15 см.
Рассмотренные свойства параллельных плоскостей намного упрощают решение многих геометрических задач.
🎦 Видео
Параллельные прямые | Математика | TutorOnlineСкачать

Параллельные прямые (задачи).Скачать

Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Параллельность прямых. 10 класс.Скачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

10 класс, 10 урок, Параллельные плоскостиСкачать

Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№65. Параллельные отрезки А1А2, В1В2 и С1С2 заключены между параллельными плоскостями α и βСкачать

7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

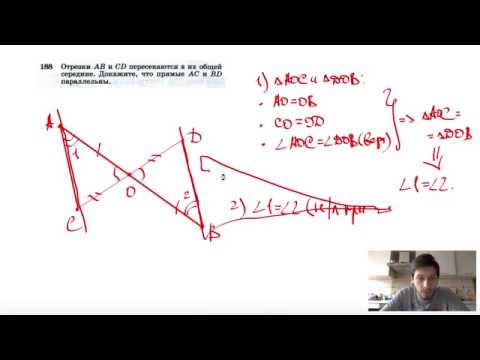
№188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АССкачать
10 класс, 11 урок, Свойства параллельных плоскостейСкачать

Признаки параллельности прямых. Первый. Доказательство.Скачать

10 класс, 5 урок, Параллельность трех прямыхСкачать

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Задачи на доказательство по геометрии. Признаки параллельности прямых.Скачать

Геометрия 10 класс : Параллельные плоскости и их свойстваСкачать