Одним из фундаментальных понятий всех происходящих в природе электромагнитных явлений выступает магнитное поле, важнейшей характеристикой которого служит напряжённость.
- Определение и формула напряжённости магнитного поля
- Физический смысл
- Закон Био-Савара-Лапласа
- Циркуляция вектора напряжённости магнитного поля
- Формулы
- Напряжённость магнитного поля в цилиндрической катушке
- Вокруг прямолинейного проводника
- В центре витка с током
- Небесная механика — один из разделов астрономии (стр. 5 )
- Закон био-савара-лапласа и его полевая трактовка — справочник студента
- Закон Био Савара Лапласа
- Закон Био-Савара-Лапласа: применение
- Применение закона Био-Савара-Лапласа в магнитном поле
- Задача на применение закона Био-Савара-Лапласа
- Закон Био — Савара — Лапласа — это… Что такое Закон Био — Савара — Лапласа?
- Формулировка
- Вывод из уравнений Максвелла
- Литература
- Закон Био — Савара — Лапласа и его применение к расчету магнитного поля
- §2. Закон Био – Савара – Лапласа
- Закон взаимодействия элементов тока (закон Лапласа-Био-Савара-Ампера). Полевая трактовка закона взаимодействия элементов тока. Релятивистская природа магнитного поля
- Изучение магнитного поля (закон Био-Савара-Лапласа)
- 🌟 Видео
Видео:Лекция 124. Преобразование Лапласа. ВведениеСкачать

Определение и формула напряжённости магнитного поля
Вокруг постоянного магнита или проводника с протекающим по нему электрическим током всегда присутствует магнитное поле. Эта одна из форм существования электромагнитного поля, естественного или искусственного происхождения. Как и всякая физическая величина, она имеет свои характеристики, одной из которых выступает напряжённость магнитного поля.
Из курса физики известно, что напряжённость магнитного поля H – это векторная (не скалярная, то есть определённым образом направленная в пространстве) величина, являющейся геометрической разницей между векторами магнитной индукции B и вектором намагниченности M.
Небольшое пояснение. Магнитная индукция B – это силовая векторная характеристика магнитного поля в конкретной точке пространства, которая характеризует силу воздействия на электрический заряд определённой величины, движущийся в этом поле.
Намагниченность M – это векторный показатель, демонстрирующий магнитное состояние тела, являющегося источником возникшего магнитного поля. Формулы, описывающие величину напряжённости магнитного поля в разных системах единиц измерения, выглядят следующим образом:
В системе СИ (Международной системе единиц):
где μ0 – магнитная постоянная, равная 4π10 −7 Гн/м, или менее точно 1,2566370614 10 -6 Н/А 2 . Единицей измерения напряжённости здесь выступает ампер на метр. 1А/м = 4π/1000Э = 0,01256637Э.
В системе СГС (сантиметр-грамм-секунда):
Здесь единицей измерения служит эрстед (Э). 1Э = 1000/4πА/м = 79,5775 А/м. При этом надо в обязательном порядке учитывать, что намагниченность зависит от магнитной проницаемости среды следующим образом:
M = ((μ-1)/4πμ)B, где μ – магнитная проницаемость, составляющая:
- для диамагнетиков (стекло, медь, вода) – 0,99999;
- для парамагнетиков (алюминий, воздух, кислород) – 1,0000;
- для ферромагнетиков: никель – 1100; железо – 8000.
Видео:Преобразование Лапласа - bezbotvyСкачать

Физический смысл
Физический смысл напряжённости находится в прямой зависимости от среды формирования магнитного поля:
- при её отсутствии или в вакууме, напряжённость и вектор магнитного поля – H и B, совпадают между собой с точностью до величины магнитной постоянной μ0;
- в магнитной среде напряжённость – H представляет собой величину воздействия «внешнего» поля. Поля, имеющего место быть при отсутствии самого магнитного материала. То есть она соответствует вектору магнитной индукции – B внешних полей воздействия.
Видео:Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

Закон Био-Савара-Лапласа
Главный закон магнитостатики, действие которого экспериментально было обнаружено в начале XIX века французскими учёными Био и Саваром, принял свою формулировку благодаря другому французскому исследователю маркизу де Лапласу. Именно он показал, что «магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока». Аналогичный вывод несколько позже был сделан исходя из двух уравнений Максвелла, составляющих совместно с выражениями для силы Лоренца теоретическую основу классической электродинамики.
В обобщённом виде закон выглядит следующим образом:
Пользуясь системой единиц СИ, для вакуума получаем:
где I – ток; dl – вектор, совпадающий и сонаправленный с протекающим током, r – модуль радиус-вектора, направленный в точку определения dB, α – угол между dl и r.
Видео:Квантовая механика 8 - Операторы. Собственные векторы и собственные значения.Скачать

Циркуляция вектора напряжённости магнитного поля
В 1826 году ещё один французский учёный – Андре Мари Ампер сформулировал теорему о циркуляции магнитного поля (позже она также была подтверждена шотландцем Максвеллом), гласящую, что «Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающий контур циркуляции».
Из которой следует, что циркуляция вектора напряжённости магнитного поля соответствует сумме свободных токов, сцепленных с контуром. Связанные токи, образованные в магнетике под воздействием внешних полей, явно здесь не присутствуют.
Видео:Оператор Набла. Градиент. Дивергенция. Ротор. Лапласиан.Скачать

Формулы
что в дифференциальной форме выглядит следующим образом:
где j – плотность тока, а c – скорость света в вакууме.
Напряжённость магнитного поля в цилиндрической катушке
Напряжённость магнитного поля в цилиндрической катушке прямо пропорциональна силе тока, зависящей, в свою очередь, от прикладываемого напряжения, а также сопротивления, определяемого числом витков катушки и обратно пропорциональна длине катушки.
В приведённой формуле:
- I – сила протекающего тока;
- n – число витков катушки;
- L – длина цилиндрической катушки.
Вокруг прямолинейного проводника
Магнитное поле, окружающее прямолинейный проводник, напрямую зависит от величины и направления протекающего тока:
Где I – величина тока, а r – расстояние точки замера от проводника.
В центре витка с током
Здесь формула расчёта напряжённости практически аналогична случаю прямолинейного проводника:
Лишь R – обозначает радиус токопроводящего витка.
Определение напряжённости магнитного поля, измерение его величины в разных местах и условиях имеет большое практическое значение. Прежде всего, потому что все мы живём в магнитном поле земли и нередко подвергаемся воздействию внеземных магнитных полей.
Кроме того, данная величина важна с электротехнических позиций, вследствие электромагнитного воздействия на физические тела, попадающие в зону влияния магнитного поля. Так большое практическое значение находит использование тороидального магнитного поля, образованного катушкой с сердечником, внутри которой оно максимально; а вне её – равняется нулю.
Видео:Лекция 125. Преобразование Лапласа. Применение.Скачать

Небесная механика — один из разделов астрономии (стр. 5 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |


Итак, по векторам r(t) и r`(t) с помощью формул (35.3) мы получили шесть оскулирующих элементов орбиты: .
На рис. 35.1 показаны оскулирующие орбиты, соответствующие векторам r(t) и r`(t).
Оскулирующие (эллипсоидальные) орбиты должны удовлетворять трем условиям:
1)проходить через точку m, в которой в данный момент времени t находится спутник;
2)проходить так, чтобы касательная к нему совпадала с вектором скорости r`(t) в этот момент времени t;
3) проходить так, чтобы один из фокусов (эллипса) орбиты располагался в притягивающем центре — точке О.
Если такие оскулирующие (эллипсы) орбиты строить непрерывно вдоль возмущенной траектории спутника, то мы получим семейство оскулирующих орбит (рис. 35.1). в результате возмущенная траектория будет являться огибающей (кривой) семейства оскулирующих орбит.
Определение оскулирующей орбиты
Оскулирующая орбита – это мгновенное (виртуальное) коническое сечение, которое определяется вектором положения и вектором скорости спутника, находящегося на возмущенной траектории, в момент времени t (на основании формул (35.2)).
Таким образом, оскулирующая орбита может считаться постоянной в пределах ограниченного отрезка времени в зависимости от заданной точности расчета траектории (рис. 35.2).
Рисунок 35.2 – Пределы применимости оскулирующей орбиты на момент t0 на интервале [t0-Δ; t0+Δ] при заданной погрешности расчета возмущающей траектории.
Тема 16. Интеграл Лапласа.
Продолжаем интегрировать движение спутника
Приведем к виду, удобному для получения еще одного интеграла, независимого от первых двух: интеграл площадей и интеграл энергии.
Для этого умножим равенство (16.1) на векторную константу площадей с первое слагаемое в (16.1) и на r x r´ — второе слагаемое, так как
Преобразуем второе слагаемое в (16.3), где имеется, так называемое двойное векторное слагаемое, которое раскрывается по правилу: «БАЦ – ЦАБ».
Применяя (16.5) к (16.3), находим
Подставляя (16.4) к (16.6)
В равенство (16.3), получаем
Где — λ — произвольная векторная константа которая взята специально со знаком «-»,для того чтобы вектор λ был направлен как будет показано ниже, в ближайшую точку орбит.
И так выражение
где rº = r / r — орт носит название в небесной механике интеграла Лапласа.
Произвольная постоянно может быть определена как обычно, по начальным условиям движения
Так как интеграл Лапласа справедлив для любого момента времени то он справедлив и для начального t0. По этому
Для выяснения физического смысла λ необходимо преобразование (16.8).
Тема №17 Физический смысл вектора Лапласа
17.1 Уравнение орбит полярных координатах.
Мы получили три интеграла:
-энергии h = v² — 2μ/r (17.3)
Наша цель: получить явные выражения для векторов положение r и вектора скорости r´в виде функции времени t и НУ r0, r´0 в t0. Чтобы достичь конечной цели нужно выяснить физический смысл константы (переменной) интегрирования с, h,. Первые две константы с, h: для них установлен физический смысл. Установим физический смысл константы λ. Для этого умножим сколярно интеграл Лапласа (17.4) на текущий радиус-вектор спутника r.


Раскроем левую часть (17.5)
Где угол v = λ,^r — как угол между вектора Лапласа и текущим радиус-вектором спутника r обозначает, как правило, v и называется истиной аномалией спутника.
С учетом (17.7) перепишем (17.5)
λrCosv = с² — μr (17.8)
Разрешая уравнение (17.8) относительно r, получаем

Обычно (17.9) записывают так (учитывая то что μ ≠ 0)

Чтобы установить физический смысл вектора Лапласа λ нужно сопоставить уравнение (17.10) с уравнением конического сечения в полярных координатах, при этом полярные константы нужно выбрать особым образом.
17.2 . Конические сечения.
Всякая кривая второго порядка есть коническое сечение.
К кривым второго порядка относят:
— вырожденный случай — прямая.


 |
 |





 |

 | |
 |  |






 |
Рис.17.2 Если π||Q, то L – парабола Рис.17.3 Если π || H, то L — гипербола
От выбора, то есть от выбора расположения начало координат О и выбора ориентировки осей координат, а так же выбора вида координат (прямоугольных, полярных) зависит вид уравнений конических сечений. Например, если выбрать начало координат О в центре симметрии кривой ориентировать оси прямоугольника С координат по оси симметрии кривой, то получается, так называемое коническое уравнение второго порядка.








O Рис.17.6 эллипс в Oxyz с полуосями
 |
Рис.17.4 если π проходит через О и касается образующей, L – прямая (два луча)
Если вместо двух переменных x и y выбрать один, так называемый лонгальный параметр Е, то уравнение (17.11) перепишем в виде двух параметрических уравнений.
x = aCosE, y = bSinE (17.12)
Если же переместить начало координат О из центра симметрии эллипса в один из его фокусов (F1 или F2) и заменить вид координат – вместо прямоугольных x и y, взять полярные координаты ρ и φ, то уравнение (17.11) перепишем так (рис. 17.7)
ρ = p / 1 + εCosφ (17.13)









Рис.17.7 Эллипс в полярных координатах
Расстояние между фокусами эллипса F1 и F2
 |
F1 F2 = 2aε (17.14)
и называется фокальным расстоянием. В формуле (17.13) — это половина хорды, проходит через один из фокусов кривой (F1 или F2) перпендикулярно оси симметрии (или точнее, большой полуоси эллипса а) на рис. 17.7 p = F1 Q и p ┴ а. Он связан с большей полуосью формулой
ε = (a² – b²) / a² (17.16)
(17.16) – эксцентриситет эллипса. Теперь сопоставляя уравнения кривой второго порядка (из аналитической геометрии) (17.13) с уравнением (17.10), заключаем, что


Уравнение (17.10) – уравнение конического сечения в полярных координатах r и v с полюсом в центре масс центрального тела, (так как исходное уравнение γ мы интегрируем в инерциальную систему координат r´ + (μ/r²)rº = 0)
Являющегося одним из фокусов (F1 или F2) конического сечения. Далее фокальный параметр орбиты p равен
и является одной из констант интегрирования эксцентриситета орбиты
ε ≡ e = λ/μ (17.19),( в небесной механике эксцентриситет обычно обозначают «е» ).
Из того, что v => φ, выясняется направления вектора Лапласа – вектор λ направлен по оси симметрии эллипса в ближайшую точку орбиты π (рис. 17.8)
 |
 |




Рис.17.8 Центр орбины в полярной СК
r = p/ 1+eCosv (17.20) ≡ (17.10) – уравнение орбиты в полярных координатах.
Из сопоставления выражения, получается как следствие интеграла Лапласа,

с каноническим выражением конических сечений
ρ = p / 1 + εCosφ (17.13)
следует, что равенство (17.10) представляет собой уравнение конического сечения (окружность, эллипсоид, парабола, гипербола) и переписывается окончательно в виде
r = p/ 1+eCosv (17.20),
р = c²/μ, ε ≡ e = λ/μ, v = μ, е > 1, то орбита — гипербола.
Всякий вектор в трехмерном пространстве должен характеризовать три параметра. Мы установили только для вектора Лапласа, нужно установить физический смысл для направления вектора Лапласа. Таким образом, два оставшихся параметра в векторе λ характеризует его направление в пространстве, которое определяется осью симметрии конического сечения и ближайшей точки орбиты фокуса.
Тема 18. Точки и линии орбиты спутника.
С помощью интеграла площадей мы установили, что орбита спутника – плоскостная кривая, лежащая в плоскости, лежащая в инерциальной системе координат. Эта кривая: замкнутая или разомкнутая и представляет собой одно из конических сечений. Это коническое сечение постоянной орбиты ориентирования внутри орбитальной плоскости. (рис. 18.1 )








Рис.18.1. Точки и линии эллиптической орбиты.
На рис. 18.1 О’ – центр симметрии конического сечения
F1 и F2 – фокусы симметрии конического сечения
π – перицентр орбиты
α – апоцентр орбиты
Оπ — линия апсид орбиты
 |
ОΩ — линии узлов орбиты
Угол v — истинная аномалия спутника
Угол ω — аргумент широты орбиты
ω = π + ωгл, если f 0.
Тема 19. Связь константы площадей энергии спутника h с большой полуосью орбиты a.
Для установления связи h и a воспользуемся интегралом энергии.
Так как интеграл энергии справедлив для любой точки орбиты, вычислим его в точке перицентра орбиты π.(рис19.1)





Но из уравнения орбиты
r = p/ 1+eCosv (17.20), получаем
vπ = 0º, rπ = p / (1 + e) = a (1 — e²)/1 +e = a (1 — e)(1 + e)/1 + e = a (1 — e)
rπ = a (1 — e), rα = a (1 + e) (19.3)
Вычислим линейную скорость спутника V в точке π, как произведение угловой скорости радиуса – вектора спутника r. Относительно фокуса О — это υπ на длину вектора r, то есть
Угловую скорость υ получим из полярной формы интеграла площадей
Но из рисунка 18.1 имеем
Дифференцируя (19.6) и учитывая, что ω – константа, получаем, что u´≡ v´ (19.7)
Тогда интеграл площадей, записывают



Получаем, что Vπ = μp / 2π = μa(1 — e²) / a(1 — e) (19.10)
После алгебраического преобразования получаем
h = — μ/a (19.11) – установлена связь константы с большой полуосью.
Тема№20. Период обращения спутника. Третий закон Кеплера.
В невозмущенном движении период обращения спутника имеет смысл только для замкнутых орбит (эллипс, окружность). Периодом обращения называется промежуток времени между двумя последовательными прохождениями спутника через одну и ту же (любую) точку орбиты.
Рис.20.1 период обращения спутника.
На рис.20.1 точка О – центральное тело
точка m — любая точка орбиты, через которую проходит спутник дважды в моменты
где T – период обращения
Установим связь Т с большой полуосью орбиты а. Для этого дважды вычислим S эллипса орбиты, один раз из геометрических соображений, другой раз из динамических соображений.
Из аналитической геодезии.
Рис. 20.2 Площадь орбитального эллипса из геометрии
S прямоугольника = 4аb
S эллипса =π ab ( 20.3)
Вычислим из динамических соображений, воспользовавшись вторым законом Кеплера, но в современной формулировке.
Где S´ – скорость изменения площади (секториальная скорость) движения спутника на орбите,
C — константа площадей
Возьмем интеграл по t от выражения (20.4)
∫ S´dt = S орбитального эллипса из динамики (20.6)
∫ ½ С dt = ½ С ( t + T – t ) = ½ μр T (20.7)
Таким образом, S эллипса из динамики = T (20.8)
Поскольку площади S эллипса из геометрии должна быть равна площади из динамики S эллипса из динамики то, приравнивая (20.3) и (20.8), получаем
p = a ( 1 – e2 ), b = a 1 – e2
T = 2πab / μр = 2πa а 1 – e2 / μ а ( 1 – e2 ) = 2π / μ/а3
Формула (20.9) связывает через константы π и μ, период обращения спутника T с большой полуосью его орбиты а. Отсюда следует, что параметр T определяем размер орбиты (полуось а), но большая полуось связана с константой энергии h по формуле.
Но mh/2 — полная энергия спутника, следовательно период обращения спутника T связан с полной энергией спутника и является одной из констант интегрирования дифференциального уравнения движения спутника.
Среднее движение спутника.
Выясним физический смысл знаменателя в формуле
Из (20.9) имеем μ/а3 = 2π / Т (20.11)
Но 2π — полный угол, который описывает радиус-вектор r за время T (период).
Следовательно величина μ/а3 есть средняя угловая скорость движения спутника по орбите. В небесной механике используется термин — среднее движение спутника обозначается «n»
Тогда формула (20.11) переписывается так
n = 2π / Т или Т = 2π / n (20.13)
Из формул (20.11, 20.12) или (20.9) следует третий закон Кеплера в современной формулировке
Из (20.14) следует третий закон Кеплера: «произведение квадрата среднего движения спутника на куб большой полуоси его орбит есть величина постоянная ».
Получим выражение с помощью (20.14) из которой следует формулировка третьего закона (Кеплера) (рис.20.3)
Рассмотрим одно центровое тело O, вокруг которого движение нескольких спутников
( проекция солнечной системы )
Рис. 20.3 Третий закон Кеплера в классической формулировке
Применим (20,14) к системе спутников m1, m2,….,
n12a13= n22a23= n32a33=…=μ (20.15)
Для двух спутников m1 и m2, получаем отношение
n12/ n22 = a23/ a13 (20.16)
Из формулы (20.17) следует третий закон Кеплера в классической формулировке ; «квадраты периодов обращения двух спутников относительно одного и того же центрального тела как
кубы больших полуосей их орбит».
Заменим в (20.16) средние движение n периодом T
(2π / Т1)2 a23 Т12 a23
(2π / Т2)2 a13 Т22 a13
Кеплер установил этот закон эмпирическим путем по Тиха Браги. Мы получили этот закон как частный случай трех законов Ньютона.
Тема№21. Связь трех констант интегрирования;
Лапласа, энергии и площадей.
Наша цель показать, что три произведения постоянного интегрирования ДУ движения спутника λ, h и с. Они являются между собой зависимыми величинами. Для этого воспользуемся интегралом Лапласа и площадей.
λ = с x r´ — μrº; c = r x r´ ( 21.1)
Возьмем в квадрат левую и правую части интеграла Лапласа
λ 2 = [ — (с x r´ + μrº)] = (с x r´)2 +2(с x r´)(μr) + μ2 (rº)2 (21.2)
λ 2 = λ 2 – как скалярный квадрат (21.3)
(с x r´)2 = │ с x r´│2 = │сv Sin (с^v)│2 = (сv)2 (21.4)
r ≡ v – двоякое обозначение вектора скорости
2(с x r´)(μrº) = 2μ (с x r´)rº = 2μ (с x r´) r/r = 2μ/ r (с x r´) r =
= 2μ/ r (r´ x r) с = 2μ/ r (- с2) = — 2μс2/ r
2(с x r´)(μrº) = — 2μс2/ r (21.5)
λ 2 = μ2 + с2h (21.6)
ТЕМА №22. Радиальная трансверсальная составляющие скорости движения спутника.
Скорость движения спутника всегда направлена по касательной к его орбите. Этот вектор скорости раскладывается на две ортогональных составляющих: радиальную и трансверсальную, рис.22.1
Рис.22.1. Радиальная и трансверсальная скорость движения спутника.
На рисунке 22.1 показана орбитальная дуга, притягивает центр О, перицентр π, вектор Лапласа λ, текущее положение спутника m в t, его радиус-вектор r и вектор скорости v, касательный к орбите в точке m.
Vr — вектор радиальной скорости спутника;
Vτ — вектор трансверсальной скорости спутника;
rº — орт радиального направления (он же орт радиус-вектора спутника )
τº — орт трансвкрсального направления
Вектор скорости спутника v можно представить разложение по ортам rº и τº, как сумму двух векторов
V = Vr rº+ Vτ τº (22.2)
Из курса физики вектор скорости V есть производная по времени то радиус — вектора r/t.
V = d/ dt (r (t)) = r´(t) (22.3)
Но радиус-вектор r (t) можно представить как произведение его модуля r (t) на орт rº(t).
r (t) = r (t) • rº(t) (22.4)
Берем производную от равенства (22.4) получаем
V = d/ dt (r (t) rº(t)) = d/ dt [r (t)] rº(t) + r (t) d/ dt[rº(t)] (22.5)
d/ dt (r (t)) = r´ (22.6)
Из курса физики производная от любого вектора r, вращающегося с угловой скоростью ω вокруг оси, проходящей через начало вектора r в направлении ωº, равна векторному произведению r, рис. 22.2 .
d/ dt (r) = ω x r (22.7)
Рис.22.2 Представление линейной скорости.
V = d/ dt (r) = ω x r (22.7)
Применим формулу (22.7´) для вычисления производной и d/ dt (rº (t)), рис.22.3.
Орт rº вращается с угловой скоростью υ´ — скорость изменения истинной аномалии со временем, от сюда следует, что υ´ ≡ ω – модуль угловой скорости (22.7´).
Орт оси вращения вектора rº есть орт сº – векторной константы площадей с.
тогда r´º = ω x rº (22.9)
или r´º = υ´сº x rº
или r´º = υ´ τº (22.10),
где τº = сº x rº (22.11).
Перепишем (22.5) с учетом (22.10)
V = Vr rº + rυ´ τº (22.12)
Сравнивая (22.12) с (22.2)
V = Vr rº+ Vτ τº (22.2), приравнивая их правые части и приравнивая скалярные множители при одинаковых ортах, получаем
Vr = r´ , Vτ = r υ´ (22.13)
Из формул (22.13) следует, что радиальная составляющая скорости отвечает за изменение длины радиуса – вектора спутника, а трансверсальная составляющая – отвечает за линейную скорость и движения спутника по виртуальной окружности радиуса r. Установим связь радиальной Vr и трансверсальной Vτ скорости спутника с параметрами орбиты: р — фокальный параметр орбиты, е – эксцентриситетом орбиты и углом υ– истинной аномалии силы.
Для этого воспользуемся двумя интегралами:
— уравнением орбиты в полярных координатах
r = p/ 1+eCosυ (22.14),
— интегралом площадей в полярных координатах
c = r²υ´, c = μp (22.15)
Дифференцируя (22.14) по t, получаем
Vr = r´ = p(e+Sinυ)υ´ p = μp eSinυ = μ / p eSinυ
Итак, Vr = μ / p eSinυ (22.16)
Для получения трансверсальной скорости Vτ как функции р, е и υ сравнивают два выражения (22.13) с (22.15)
c = r²υ´ Vτ = с/r (22.17)
Или с учетом (22.14) и (22.15), находим
Vτ = μ / p (1+eCosυ) (22.18)
Формулы (22.16) и (22.18) устанавливаем связь Vr и Vτ с направлением орбиты р, е и υ. Полезны формулы, связи скорости:
V = 2μ / r + h (22.20) — интеграл энергии.
ТЕМА №23. Эксцентрическая аномалия (геометрическая интерпретация) спутника.
Для определения положения спутника на заданной орбите в небесной механике используется три аномалии:
Истинная была введена в разделе уравнения орбиты нормальных координат. Она отслеживает истинный угол вращения спутника рис.23.1.
Рис. 23.1 Истинная аномалия
Истинная аномалия более сложным образом связана со временем t. Эксцентрическая аномалия Е связана со временем Е(t) более простой формулой, чем υ(t).
Средняя аномалия М связана со временем наиболее просто по линейному закону.
Все три аномалии связаны между собой.
υ ( E ( M (t))) = υ (t) (23.1)
Покажем на рис.23.2 геометрическую интерпретацию эксцентрической аномалии.
Рис. 23.2 Эксцентрическая аномаоия
На рис.23.2 О’ – центр симметрии орбитального эллипса, О – притягивающий центр
( центральное тело ), m – положение спутника на орбите в текущий момент времени, вектор qm перпендикулярен линии апсид Оπ,
угол πОm = υ – истинная аномалия спутника, которая отслеживает истинный угол υ поворота радиус – вектора спутника r относительно вектора Лапласа λ ( или линии апсид ), угол πО’m’ = Е – эксцентрическая аномалия спутника, вершина угла Е находится не в центре масс тела, а в центре симметрии орбитального эллипса, точка m’ – виртуальная точка движения по окружности радиуса в центре с центром симметрии эллипса и получается как результат пересечения перпендикулярно вектору qm с окружностью.
Из рис.23.2 видно, что две точки m и m’ при движении спутника m по орбите сливаются в одну точку в двух случаях:
1. когда спутник находится в перицентре π,
2. когда спутник находится в апоцентре α.
Правильное применение терминов перицентр ( перигей ), апоцентр ( апогей ) и т. п.
Когда центральное тело безымянное или же обсуждается задача двух без относительно какого либо центрального тела, то точки орбиты π и α называется перицентром и апоцентром. Если же уентральное тело имеет имя, или решение конкретной реальной задачи двух тел, то название точек меняется ( см. в таблице ).
центральное тело перицентр апоцентр
Земля( спутник: Луна, иск. Спутник ) перигей апогей
Солнце ( спутник 6 Земля, Венере и т. д. ) перигелий афелий
Луна ( иск. спутник ) переселений апоселений
Тема№24. Эксцентрическая аномалия спутника. Аналитическая связь двух аномалий.
Для получения формулы выражающие эксцентриситет аномалии через истинную или наоборот введем три орбитальных системы координат. Орбитальная система — основная плоскость совпадает с плоскостью орбиты.
1. Система координат Oξη с началом притягивающим центре О и осью Oξ абсцисс, направленный по линии апсид Oπ.
α m линия апсид полярная ось
Рис. 24.1 Связь истинной и эксцентрической аномалии.
2.Полярная система координат с полюсом в точке О и полярной осью направлена по линии апсид с полярными координатами r и υ.
r – полярное расстояние
υ – полярный угол
( в небесной механике r – модуль радиус-вектора спутника, υ – истинная аномалия спутника)
3. Прямоугольная система координат О´xy с началом O´ в центре симметрии орбиты и осью абсцисс O´y направленной по линии апсид. Уравнение орбиты спутника в системе координат О´xy имеет вид (см. аналитический геометрический метод ).
Уравнение орбиты спутника в полярной системе координат ( r,υ) имеет вид
r = p/ 1+ eCosυ (24.2)
где p = a(1-e²), e² = a² – b² / a² , b = a 1 — e² (24.3)
ae = О´О– полуфокальное расстояние
Уравнение орбиты спутника в параметрической форме
Уравнение дано без выводов, где Е — параметр. Если подставить (24.4) в (24.1),то получим тождество, что свидетельствует о правомерности введение уравнения (24.4).уравнение орбиты в координатах ξ и η (из рис. 24.1)
ξ = rCosυ, η = rSinυ (24.5)
С другой стороны, с центром (24.4) и рис.24.1 получаем
ξ = x – ae = aCosE – ae = a(CosE – e)
η = y = bSinE = a 1 — e² Sin E
y = a 1 — e² Sin E (24.6)
Сопоставляя (24.6) и(24.5), находим искомую связь
rCosυ = a(CosE — e)
rSinυ = a 1 — e² Sin E (24.7)
Заменим r с помощью формулы
r = a(1 — eCosE) (24.8),
которая получается из рис.24.1 по теореме Пифагора
r² = ξ² + η² = [a(CosE – e)]² + (a 1 — e² Sin E )²
Подставляя (24.8) в (24.7), получаем окончательно –
Cosυ = CosE – e / 1 – eCosE (24.9)
Sinυ = 1 — e² Sin E / 1 – eCosE (24.9)
Формулы (24.9) устанавливают связь Е и υ в одну сторону: Е => υ. Получим обратную связь:
υ =>Е. Можно воспользоваться формулой для тангенса половинного угла
tg α/2 = 1 – Cosα/ 1 + Cosα (24.10)
Заменим в (24.10) α на υ
tg υ/2 = 1 – Cosυ/ 1 + Cosυ (24.11)
Подставив в (24.11) равенство (24.9), получим окончательно
tg υ/2 = 1 + e / 1 – e tg E/2 (24.12)
tgE/2 = 1 + e / 1 – e tg υ/2 (24.13),
формулы (24.9),(24.12),(24.13) устанавливают связь Е υ.
Тема№25. Уравнение Кеплера.
Уравнение Кеплера — последний четвертый независимый интеграл решаемого дифференциального уравнения.
Уравнение устанавливает связь угла поворота равенств со временем t. Для получения этой связи воспользуемся интегралом площадей в полярной форме
Где υ´=dυ/dt — скорость измерения истинной аномалией υ со временем t.
Из (25.2) получаем интеграл r²•dυ/dt = c или разделяя переменные υ и t, так чтобы они находились в различных частях равенства.
и интегрируя t(υ)
Интеграл (25.4) сложен
∫ a(1 — e²) /1 + eCosυ dυ = ?
Необходимо привести его к табличному виду
r = a ( 1 – eCosE ) (25.5)
Остается найти dυ через dE.
Для этого воспользуемся формулой
Cosυ = CosE – e / 1 – eCosE (25.6)
Дифференцируя по υ левую часть и по Е правую, находим
-SinEdE (1 – eCosE) – (CosE – e)(eSinE)
Завершить самостоятельно; используем для Sinυ формулу (24.9)
Итог: dυ = 1 — e² dE / 1 — eCosE (25.7)
Подставляя (25.7), (25.5) в (25.4), получаем
∫ a²(1 — eCosE)² 1 — e² / 1 – eCosE dE = ∫ cdt
∫ (1 — eCosE) dE = ∫ c / a² 1 — e² dt (25.8)
Выражение (25.8) легко интегрируется.
Интегрируя левую часть (25.8), находим
E – eSinE = E – eSinE (25.9)
Учитывая, что при υ=0, эксцентрическая аномалия Е так же равна нулю.
Интегрируя правую часть (25.9), находим
t = t = (t — tπ) = n (t — tπ) (25.10) a 1 — e² a² 1 — e² a 1 — e²
Из третьего закона Кеплера n²a3 = μ имеем n = μ/а3
Где n — среднее движение спутника,
а — большая полуось орбиты,
μ — гравитационный параметр центрального тела.
Объединяя (25.10) и (25.9) согласно (25.8), находим окончательно, что
E – eSinE = n (t — tπ) (25.11)
Выражение (25.11) носит название в небесной механике – уравнение Кеплера.
Оно связывает эксцентрическую аномалию спутника Е со временем t через три параметра : e, a, tπ — константы.
Уравнение Кеплера – четвертый интеграл r´´ + (μ/r²)rº = 0, для четвертого интеграла достаточно построить траекторию спутника и выразить явно радиус спутника r как функцию времени t: r(t).
Тема№26. Средняя аномалия спутника.
В уравнение Кеплера Е – eSinE = n (t — tπ) (26.1)≡(25.11),
выясним физический смысл правой части n (t — tπ) — ?
Параметр n — есть угловая скорость (средн.) движения спутника по орбите. Тогда произведение n (t — tπ) представляет собой угол, который обозначен через μ.
При текущем времени t, равном tπ, из формулы (26.2) следует, что μ = 0. Отсюда вытекает, что угол μ отсчитывается от точки π — перицентра. Угол μ в небесной механики называется средней аномалией спутника. И этот угол отслеживает движение фиктивной точки по окружности с постоянной угловой скоростью n. (см. рис.26.1). Момент tπ истинная υ и эксцентрическая Е аномалии равны 0. В tπ : υπ = 0, Еπ = 0 и как следует из (26.2), Мπ так же равняется 0. То есть образованные все три аномалии учитываются от одного и того же направления – линии апсид (или, что то же самое от вектора Лапласа ).
В небесной механики вводят понятие средней аномалии спутника в начальную эпоху t0, по формуле, на основе (26.2)
M0 = M(t0) = n (t0 — tπ) (26.3)
Тогда выражение (26.2) для средней аномалии M перепишется так:
M = M0 + n (t – t0) (26.4)
Рис.26.1 три аномалии спутника: υ(t), E(t), M(t).
Подстановкой в (26.4) формулы (26.3) самостоятельно проверить совпадение с формулой (26.2) С учетом введенных обозначений для средней аномалии M уравнение Кеплера (25.11) ≡ (26.1) обычно записывают в виде
E – eSinE = M (26.5) .
Тема№27. Итеративный метод решения уравнения Кеплера.
Уравнение Кеплера M = E – eSinE (27.1) ≡ (26.5)
в одну сторону решается явно (то есть когда дана эксцентрическая аномалия Е и ищется средняя аномалия спутника M, при условии, что эксцентриситет известен). В обратную сторону (то есть когда дано M, а ищется Е то нет в математике способов решения таких нелинейных (трансцендентных уравнений) явно аналитического решения получить не возможно, то есть
M => E — проблема аналитического решения.
Для таких трансцендентных уравнений (когда искомая функция входит под знак тригонометрической функции так и явно) существует множество численных методов, мы рассмотрим один — итерационный способ решения. Этот способ применим только тогда, когда
Итеративная формула имеет вид
Где k = 1, 2…. – порядковый номер итерации
В качестве начального значения Е (0) можно принять любое число, например Е(0) = 0º,или Е(0) =М (в последнем случае на одну итерацию будет меньше).
к = 1 Е(1) = М + e sin Е(0)
k = k E(k) = M + e sin Е(k-1)
продолжая до тех пор пока не выполнится критерии окончания итерации: два последовательных значения эксцентрической аномалии E(k) и Е(k-1) не станут различаться между собой на заданную величину погрешности расчетов ε.
│E(k) — Е(k-1)│≤ ε ( в радианах ).
Тема 28. Связь трёх аномалии спутника v, Е и М со временем t полёта.
Приведем здесь сводку формул, полученных в предыдущих разделах, связывая три аномалии спутника v, Е и М, как между собой, так и со временем t.
tg (v/2) = 1 + e /1 — e tgE/2 (28.1)
tg (Е/2) = 1 + e /1 — e tgυ/2 (28.2)
М = Е – е sin E (28.3)
M = M0 + n(t – t0) (28.5)
С помощью формул (28.7) решается все множество задач связанных с полетом спутника от одной точки орбиты до другой. В этих задачах вычисляется либо время полета между двумя точками либо угол поворота.
Видео:Александр Чирцов: ротор, дивергенция и градиентСкачать

Закон био-савара-лапласа и его полевая трактовка — справочник студента
1.3. Закон Био – Савара – Лапласа и его применение к расчету магнитного поля.
Французские физики Ф. Савар и Ж.Б. Био изучали магнитное поле, создаваемое проводниками с постоянным током различной формы. На основании многочисленных опытов они пришли к выводу, что магнитная индукция поля проводника с током пропорциональна силе тока I, зависит от формы и размеров проводника, а также от расположения рассматриваемой точки по отношению к проводнику.
Био и Савар пытались получить самый общий закон – для проводника любой формы и любой точки поля. Однако сделать это им не удалось. По их просьбе этой проблемой занялся французский математик П.С.Лаплас. Он высказал важную гипотезу о том, что при наложении магнитных полей справедлив принцип суперпозиции, т.е. принцип независимости действия полей.
Если имеется несколько проводников с током, каждый из которых создает в исследуемой точке магнитное поле с индукциями …, то результирующая магнитная индукция будет равна векторной сумме всех: .
Если перейти к малым отрезкам провода с током, то суммирование надо заменить интегрированием и тогда индукция , создаваемая всем проводником с током I, будет равна: где– индукция, создаваемая элементом длины проводника dℓ, интегрирование проводится по всей длине проводника.
Лаплас обобщил экспериментальные результаты Био и Савара в виде дифференциального закона, называемого законом Био – Савара – Лапласа, по которому магнитная индукция , создаваемая в некоторой точке А элементом проводника dℓ с током I, определяется формулой

Таким образом, магнитную индукцию поля, создаваемую в вакууме током I, текущим по проводу конечной длины ℓ и любой формы, можно найти по формуле
 |
Магнитное поле в центре кругового проводника с током. Рассмотрим круговой проводник с током, изображенный на рис.1.8.
Все элементы данного проводника dℓ создают в его центре (точке А) магнитные поля одинакового направления – вдоль нормали к площади витка.
Поэтому, как и в предыдущем случае, сложение векторов можно заменить сложением их модулей. Элементы dℓ перпендикулярны R и sinα=1. Используя закон Био-Савара-Лапласа, получим:
 |
Магнитное поле прямолинейного проводника с током. Представим себе ток, текущий по тонкому прямому проводу бесконечной длины (рис. 1.9). Возьмем произвольную точку А на расстоянии R от проводника.
Согласно правилу правого винта (буравчика), векторы от каждого элемента тока dℓi имеют одинаковое направление, перпендикулярное плоскости чертежа (на нас). Поэтому сложение векторов можно заменить сложением их модулей.
При суммировании всех будет меняться угол α между r и dℓ, поэтому выберем α в качестве переменной интегрирования. Выразим через α все остальные величины, полагая, что отрезок АD ≈ r из-за малости dℓ.

 |
В данном выражении α1 и α2 — значения угла α для крайних точек проводника. Если прямолинейный проводник бесконечно длинный, то α1 = 0, α2 = π. Магнитная индукция в любой точке поля такого проводника с током:
 |
Напомним, что линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей.
Магнитное поле соленоида. Если витки соленоида расположены вплотную друг к другу, то соленоид можно рассматривать как систему последовательно соединенных круговых токов одинакового радиуса с общей осью.
Обозначим через L длину соленоида, а через n — число витков, приходящихся на единицу длины соленоида. Магнитная индукция поля соленоида В равна геометрической сумме магнитных индукций Вi полей всех его витков.
Если L>>R (радиуса витков), тогда В в точке А, лежащей на оси вдали от концов такого соленоида, вычисляется по формуле (без вывода): В = μ0nI.
Видео:Основные физические понятия технической электродинамики, 1978Скачать
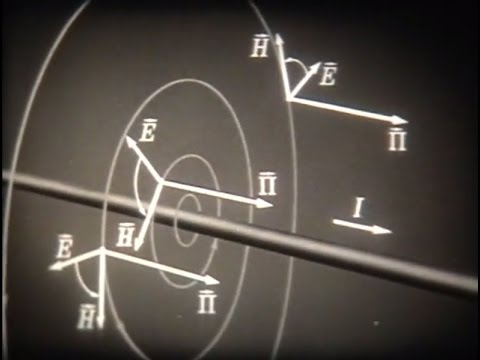
Закон Био Савара Лапласа
Закон Био Савара Лапласа — Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
- Закон Био-Савара-Лапласа для некоторых токов:
- Магнитное поле прямого тока: .
- Магнитное поле кругового тока: .
- Обозначения:
- dB — магнитная индукция;
- dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током;
— магнитная постоянная;
- μ — относительная магнитная проницаемость (среды);
- I — сила тока;
- R — расстояние от провода до точки, где мы вычисляем магнитную индукцию;
- α — угол между вектором dl и r.
- В современной формулировке закон Био — Савара — Лапласа чаще рассматривают как следствие двух уравнений Максвелла для магнитного поля при условии постоянства электрического поля:
где квадратными скобками обозначено векторное произведение, r — положение точек контура γ, dr — вектор элемента контура (ток течет вдоль него); μ0 — магнитная постоянная; r,r0 — единичный вектор, направленный от элемента контура к точке наблюдения.
В принципе контур γ может иметь ветвления, представляя собой сколь угодно сложную сеть. В таком случае под выражением, приведенным выше, следует понимать сумму по всем ветвям, слагаемое же для каждой ветви является интегралом приведенного выше вида (контур интегрирования для каждой ветви может быть при этом незамкнутым).
В случае простого контура, ток I одинаков на всех участках контура и может быть вынесен за знак интеграла. (Это справедливо отдельно и для каждого неразветвленного участка разветвленной цепи).

где — вектор, описывающий кривую проводника с током I, r — модуль , — вектор магнитной индукции, создаваемый элементом проводника .
Видео:Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

Закон Био-Савара-Лапласа: применение
В предыдущей статье мы подробно поговорили про магнитное поле. Данная статья является продолжением этой темы и мы поговорим про закон Био-Савара-Лапласа в магнитном поле и его применение.
Применение закона Био-Савара-Лапласа в магнитном поле
Полученное в предыдущей статье выражение для магнитного поля dB, сечения с током I длины dl:
Мы можем объединить всю длину любой изогнутой или даже запутанной направляющей.
Затем мы получим криволинейный интеграл, определяющий поле B, данное в этом руководстве.
Этот интеграл выражает закон Био-Савара-Лапласа, что в принципе позволяет ему получить поле B из любого руководства. Условие состоит в том, что мы можем интегрировать сложную кривую. Численные методы могут быть незаменимы здесь.
Задача на применение закона Био-Савара-Лапласа
Задача состоит в том, чтобы найти магнитное поле B на оси кругового контура с радиусом и на расстоянии x от его центра, когда через контур течет сила тока I. Разобьем петлю тока на бесконечно малые участки для d. Поле dВ одной такой секции находятся на основании закона Био-Савара-Лапласа:
Вектор dB делится на две составляющие: параллельно оси x dBx и перпендикулярно оси x dBy. Компонент dBy будет стерты при цикле контура и эти компоненты не будут дополнительно рассмотрены. Для ситуации, показанной на картинке
мы можем написать
В середине цикла, когда x уменьшается до нуля (x = 0), поле B имеет значение
Для плотно намотанной катушки с N обмотками
Видео:ДивергенцияСкачать

Закон Био — Савара — Лапласа — это… Что такое Закон Био — Савара — Лапласа?
Закон Био́—Савара—Лапла́са — физический закон для определения модуля вектора магнитной индукции в любой точке магнитного поля, порождаемого постоянным электрическим током на некотором рассматриваемом участке.
Был установлен экспериментально в 1820 году Био и Саваром.
Лаплас проанализировал данное выражение и показал, что с его помощью путём интегрирования, в частности, можно вычислить магнитное поле движущегося точечного заряда, если считать движение одной заряженной частицы током.
Формулировка
Пусть постоянный ток течёт по контуру γ, находящемуся в вакууме, — точка, в которой ищется поле, тогда индукция магнитного поля в этой точке выражается интегралом (в системе СИ)
Направление перпендикулярно и , то есть перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление , если поступательное движение буравчика соответствует направлению тока в элементе. Модуль вектора определяется выражением (в системе СИ)
Векторный потенциал даётся интегралом (в системе СИ)
Вывод из уравнений Максвелла
Закон Био — Савара — Лапласа может быть получен из уравнений Максвелла для стационарного поля. При этом производные по времени равны 0, так что уравнения для поля в вакууме примут вид (в системе СГС)
где — плотность тока в пространстве. При этом электрическое и магнитное поля оказываются независимыми. Воспользуемся векторным потенциалом для магнитного поля (в системе СГС):
Калибровочная инвариантность уравнений позволяет наложить на векторный потенциал одно дополнительное условие:
Раскрывая двойной ротор по формуле векторного анализа, получим для векторного потенциала уравнение типа уравнения Пуассона:
Его частное решение даётся интегралом, аналогичным ньютонову потенциалу:
Тогда магнитное поле определяется интегралом (в системе СГС)
аналогичным по форме закону Био — Савара — Лапласа. Это соответствие можно сделать точным, если воспользоваться обобщёнными функциями и записать пространственную плотность тока, соответствующую витку с током в пустом пространстве. Переходя от интегрирования по всему пространству к повторному интегралу вдоль витка и по ортогональным ему плоскостям и учитывая, что
получим закон Био — Савара — Лапласа для поля витка с током.
Литература
Видео:Дивергенция векторного поля. Гидродинамическая аналогия. Теорема Остроградского.Скачать

Закон Био — Савара — Лапласа и его применение к расчету магнитного поля
Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774—1862) и Ф. Саваром (1791—1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.
Закон Био — Савара — Лапласа для проводника с током I, элемент которого dl создает в некоторой точке А (рис. 164) индукцию воля dВ, записывается в вид
где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r — радиус-вектор, проведенный из элемента dl проводника в точку А поля, r — модуль радиуса-вектора r. Направление dВ перпендикулярно dl и r, т. е.
перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции.
Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление dВ, если поступательное движение винта соответствует направлению тока в элементе.
Модуль вектора dВ определяется выражением
- где a — угол между векторами dl и r.
- Для магнитного поля,как и для электрического, справедливпринцип суперпозиции:магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторнойсумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
- (110.3)
Расчет характеристик магнитного поля (В и H) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био — Савара — Лапласа совместно с принципом суперпозиции позволяет довольно просто рассчитать конкретные поля. Рассмотрим два примера.
1. Магнитное поле прямого тока — тока, текущего по тонкому прямому провод бесконечной длины (рис. 165). В произвольной точке А, удаленной от оси проводника
 |
Рис. 164Рис. 165
на расстояние R, векторы dВ от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа (“к нам”). Поэтому сложение векторов dВ можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол a(угол между векторами dl и г), выразив через него все остальные величины. Из рис. 165 следует, что
(радиус дуги СD вследствие малости dl равен r, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (110.2), получим, что магнитная индукция, создаваемая одним элементом проводника, равна
Таккак угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (110.3) и (110.4),
- Следовательно, магнитная индукция поля прямого тока
- (110.5)
2. Магнитное поле в центрекругового проводника с током (рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от витка.
Поэтому сложение векторовdВ можно заменить сложениемих модулей.
Так как все элементы проводника перпендикулярны радиусу-вектору (sina=1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно (110.2),
- .
- Тогда
- .
- Следовательно, магнитная индукция поля в центре кругового проводника с током
- .
§ 111. Закон Ампера. Взаимодействие параллельных токов
Магнитное поле (см. § 109) оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы.
Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле,прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длиной dl проводника на магнитную индукцию В:
Направление вектора dF может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следуетправило левойруки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.
Модуль силы Ампера (см. (111.1)) вычисляется по формуле
где a — угол между векторамиdI и В.
Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I1 и I2; (направления токов указаны на рис. 167), расстояние между которыми равно R.
Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I1 на элемент dl второго проводника с током I2.
Ток I1 создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление вектора B1 задается правилом правого винта, его модуль по формуле (110.5) равен
Направление силы dF1, с которой полеВ1 действует на участок dl второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол a. между элементами тока I2 и вектором В1 прямой, равен
- ,
- Рис. 167
- или, подставляя значение для В1, получим
- (111.3)
- Рассуждая аналогично, можно показать, что сила dF1 с которой магнитное поле тока I2 действует на элемент dl первого проводника с током I1, направлена в противоположную сторону и по модулю равна
Сравнение выражений (111.3) и (111.4) показывает, что
т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой
Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (111.5).
§ 112. Магнитная постоянная. Единицы магнитной индукции и напряженности магнитного поля
Если два параллельных проводника с током находятся в вакууме (m=1), то сила взаимодействия на единицу длины проводника, согласно (111.5), равна
Для нахождения числового значения m0 воспользуемся определением ампера, согласно которому при I1=I2=1A и R=1 м =2·10-7 Н/м. Подставив это значение в формулу (112.1), получим m0=4p·10-7 Н/А2=4p·10-7 Гн/м, где генри (Гн) — единица индуктивности (см. § 126).
Закон Ампера позволяет определить единицу магнитной индукции В. Предположим, что элемент проводника dl с током I перпендикулярен направлению магнитного поля. Тогда закон Ампера (см. (111.2)) запишется в виде
- ,
- откуда
- .
- Единица магнитной индукции — тесла (Тл): 1 Тл — магнитная индукция такого однородного магнитного поля, которое действует с силой 1 Н на каждый метр длины
- прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику проходит ток 1 А:
- 1 Тл==1 Н/(А·м).
- Таккак m0=4·10-7 Н/А2, а в случае вакуума (m=1), согласно (109.3), В=m0Н, то для данного случая
- .
- Единица напряженности магнитного поля —ампер наметр (А/м): 1 А/м — напряженность такого поля, магнитная индукция которого в вакууме равна 4p·10-7 Тл.
- § 113. Магнитное поле движущегося заряда
Каждый проводник с током создает в окружающем пространстве магнитное поле. Электрический же ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что любой движущийся в вакууме или среде заряд создает вокруг себя магнитное поле.
В результате обобщения опытных данных был установлен закон, определяющий поле В точечного заряда Q, свободно движущегося с нерелятивистской скоростью v. Под свободным движением заряда понимается его движение с постоянной скоростью.
Этот закон выражается формулой
где r — радиус-вектор, проведенный от заряда Q, к точке наблюдения М (рис. 168). Согласно выражению (113.1), вектор В направлен перпендикулярно плоскости, в которой расположены векторы v и г, а именно: его направление совпадает с направлением поступательного движения правого винта при его вращении от v к г. Модуль магнитной индукции (113.1) вычисляется по формуле
где a — угол междувекторами v и г.
Сравнивая выражения (110.1) и (113.1), видим, что движущийся заряд по своим магнитным свойствам эквивалентен элементу тока:
Приведенные закономерности (113.1) и (113.2) справедливы лишь при малых скоростях (váác) движущихся зарядов, когда электрическое поле свободно движущегося заряда можно считать электростатическим, т. е. создаваемым неподвижным зарядом, находящимся в той точке, где в данный момент времени расположен движущийся заряд.
| Рис. 168 |
Формула (113.1) определяет магнитную индукцию положительного заряда, движущегося со скоростью v. Если движется отрицательный заряд, то Q. надо заменить на —Q. Скорость v — относительная скорость, т. е.
скорость относительно наблюдателя. Вектор В в рассматриваемой системе отсчета зависиткак от времени, так и от положения точки М наблюдения.
Поэтому следует подчеркнуть относительный характер магнитного поля движущегося заряда.
Впервые поле движущегося заряда удалось обнаружить американскому физику Г. Роуланду (1848—1901). Окончательно этот факт был установлен профессором Московского университета А. А.
Эйхенвальдом (1863—1944), изучившим магнитное поле конвекционного тока, а также магнитное поле связанных зарядов поляризованного диэлектрика. Магнитное поле свободно движущихся зарядов было измерено академиком А. Ф.
Иоффе, доказавшим эквивалентность, в смысле возбуждения магнитного поля, электронного пучка и тока проводимости.
§ 114. Действие магнитного поля на движущийся заряд
Опыт показывает, что магнитное поле действует не только на проводники с током (см. § 111), но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой
где В — индукция магнитного поля, в котором заряд движется.
Направление силы Лоренца определяется с помощьюправила левой руки: если ладонь левой руки расположить так, чтобы в нее входил векторВ, а четыре вытянутых пальца направить вдоль вектора v (для Q>0 направления I и v совпадают, дня Q
Видео:#8 Ротор/Дивергенция/ГрадиентСкачать

§2. Закон Био – Савара – Лапласа
Автор Чивилев Виктор Иванович 383 статьи
В 1820 году французские учёные Ж. Био и Ф. Савар исследовали магнитные поля, создаваемые в воздухе прямолинейным током, круговым током, катушкой с током и т. д. На основании многочисленных опытов они пришли к следующим выводам:
– магнитная индукция в произвольной точке поля зависит от расположения этой точки по отношению к проводу с током;– магнитная индукция зависит от конфигурации (формы и размеров) провода с током;
– во всех случаях модуль вектора индукции магнитного поля, создаваемого тонким проводом с током, пропорционален силе тока.
Био и Савар пытались получить общий закон, позволяющий вычислить магнитную индукцию в каждой точке поля, создаваемого электрическим током, текущим в проводнике любой формы. Но сделать им это не удалось, и они обратились к известному французскому математику, физику и астроному П. Лапласу.
Лаплас учёл векторный характер магнитного поля и высказал важную гипотезу о том, что индукция B→vec в каждой точке магнитного поля любого проводника с током представляет собой векторную сумму индукций ΔB→iDelta vec_i магнитных полей, создаваемых каждым достаточно малым участком проводника (элементом тока):
Этим Лаплас предположил, что при наложении магнитных полей справедлив принцип суперпозиции, то есть принцип независимого действия магнитных полей, создаваемых несколькими источниками полей.
Обобщив результаты экспериментов Био и Савара, Лаплас пришёл к выводу, что модуль вектора магнитной индукции ΔBDelta B поля, создаваемого элементом тока в исследуемой точке CC (рис. 3), пропорционален силе тока II, длине элемента тока ΔlDelta l, синусу угла αalpha между направлением тока и направлением на исследуемую точку СС и обратно пропорционален квадрату расстояния rr до точки CC.
Направлен же вектор ΔB→vec перпендикулярно плоскости, проходящей через элемент тока и исследуемую точку, причём направление тока в элементе тока и направление поля в исследуемой точке СС связаны правилом буравчика: при движении острия буравчика в направлении тока вращение рукоятки буравчика показывает направление поля в точке CC. Остриё буравчика помещается, естественно, вблизи элемента тока. На рис. 3 поле в точке CC направлено за плоскость чертежа и обозначено поэтому крестиком.
Приведём для справки, но не для запоминания, полученную Лапласом формулу, выражающую закон Био – Савара – Лапласа:
Здесь коэффициент пропорциональности kk зависит от выбора системы единиц. В системе СИ k=10-7k=10^ ед. СИ.
Следует заметить, что правило буравчика при установлении связи между направлением тока и поля можно применять и в обратном порядке, то есть вращать буравчик так, чтобы его остриё, помещённое в исследуемую точку, двигалось по направлению вектора индукции магнитного поля, а конец рукоятки двигался в направлении тока. Проверьте это для случая, изображённого на рис. 3. Такой подход особенно удобен для витка с током при нахождении направления магнитного поля внутри витка (рис. 4).
То, что в законе Био – Савара – Лапласа модуль вектора индукции магнитного поля, создаваемого элементом тока в некоторой точке, пропорционален силе тока и длине элемента тока, легко запомнить, так как это следует непосредственно из принципа суперпозиции магнитных полей.
Действительно, увеличим ток в элементе тока в два раза.
Тогда модуль вектора магнитной индукции поля, создаваемого в некоторой точке этим элементом, увеличится тоже в два раза, не изменив направления, поскольку элемент тока с током 2I2I можно представить как два плотно прижатых друг к другу элемента тока с токами II в каждом и применить принцип суперпозиции для полей, создаваемых этими двумя элементами. Аналогичные рассуждения будут и при увеличении тока в любое число раз. Это доказывает, что модуль вектора магнитной индукции пропорционален току. Похожие рассуждения можно провести и в отношении длины элемента тока.
Следует отметить одно полезное следствие из закона Био – Савара – Лапласа. Поле, создаваемое элементом тока в произвольной точке AA (рис. 3) на оси элемента, равно нулю, т. к. для этой точки sin α=0 extrm: alpha = 0.
Это легко запомнить, если учесть, что при попытке найти направление поля в точке АА с помощью правила буравчика мы столкнёмся с неопределённостью направления поля, что указывает на то, что поле в этой точке не имеет направления, то есть отсутствует.
Попробуйте применить правило буравчика в этом случае.
В качестве самостоятельного упражнения полезно объяснить с помощью закона Био – Савара – Лапласа и правила буравчика ход магнитных силовых линий на всех рисунках школьного учебника.
Видео:Олегу Тинькову запрещён вход на Мехмат МГУСкачать

Закон взаимодействия элементов тока (закон Лапласа-Био-Савара-Ампера). Полевая трактовка закона взаимодействия элементов тока. Релятивистская природа магнитного поля
Эксперименты
Х.Эрстеда и А.Ампера в 1820г. показали, что
магнитная стрелка возле провода
поворачивается при пропускании тока
по проводу, и два провода с током
притягиваются или отталкиваются в
зависимости от направления токов в них.
— закон
Био-Савара-Лапласа-Ампера (формула
Грассмана). Гн/м
— сила, с которой
элемент тока первого контура
png»>действует на элемент тока второго
контура.
Если элементы токов лежат в плоскости
рис.
68, то направление этой силы совпадает
с направлением нормали.
Закон
Био-Савара-Лапласа–Ампера экспериментально
проверить нельзя, но следствия из него
подтверждаются на практике.
Во всех точках
пространства, окружающего произвольный
ток, всегда существует обусловленное
этим током поле сил, которое по сложившейся
исторически терминологии называется
магнитным полем.
— закон
Био-Савара-Лапласа для расчета индукции
магнитного поля, создаваемого элементом
тока в некоторой точке.
Экспериментально
проверить эту формулу нельзя, но можно
рассчитать индукцию магнитного поля,
созданного всем контуром с током,
используя установленный на опыте принцип
суперпозиции магнитных полей: .
5jcV/img-08tjYP.png»>-лишь
формальная запись, на практике
интегрирование возможно лишь для
проекций вектора магнитной индукции.
Если
задана объемная плотность тока,
Магнитное
поле порождается движущимися зарядами
(токами). Если скорость направленного
движения зарядов в проводнике ,
то. Тогда:
150 Тл — получена в виде импульса.
Кулона) непосредственно следует, что
напряженность поля неподвижного
точечного заряда q
на расстоянии r
от него можно представить как
где k— постоянная
вид, которой зависит от выбора системы
отсчета, в системе СИ ;
ε0
— электрическая
постоянная; —
радиус-вектор, проведенный из центра
поля, в котором расположен зарядq,
до интересующей нас точки.
Напряженность
поля в системе СИ выражается ввольтах
на метр
(В/м). В зависимости от знака заряда q
вектор направлен так же, как и
png»>(для
положительного заряда), или противоположно
ему (для отрицательного заряда).
По существу, формула
выражает не что иное, как закон
Кулона,
но в «полевой» форме.
Вся совокупность экспериментальных
фактов показывает, что этот закон
справедлив для расстояний от 10 см до
нескольких километров, и пока нет никаких
оснований ожидать, что этот закон не
выполняется и при больших расстояниях.
Напряженность
поля системы точечных неподвижных
зарядов равна векторной сумме
напряженностей полей, которые создавали
бы каждый из зарядов в отдельности:
Релятивистская
природа магнитного поля.
В ряде современных
учебных курсов по физике, изданных в
течение последнего десятилетия появилось
и стремительно распространяется
воззрение на магнитное поле как на
релятивистский эффект.
Магнитное поле
трактуется не как самостоятельная
физическая материальная сущность и
даже не как одна из форм проявления
электромагнитного поля, а лишь как
процесс, релятивистский эффект,
возникающий в пространстве, окружающем
точечные заряды, вследствие конечной
скорости передачи изменений величины
электрического поля через пространство.
/Цитата 1/ Из
формул полей (8.1) и (8.2) вытекает весьма
замечательный вывод: возникновение
магнитного поля является чисто
релятивистским эффектом, вследствие
наличия в природе предельной скорости
,
равной скорости света в вакууме.
Если бы эта
скорость была бесконечной (соответственно
и скорость распространения взаимодействий),
никакого магнетизма вообще не существовало
бы.
В самом деле,
рассмотрим свободный электрический
заряд. В системе отсчета где он покоится, существует только
электрическое поле. А это значит, согласно
(8.1), что в любой другой
png»>-
системе отсчета, если бы,
никакого магнитного поляне возникало бы. Оно возникает только
из-за конечности,
т.е.
в конечном счете вследствие
релятивистского эффекта
Формулы (8.1) и (8.2)
в источнике представлены так
и — напряженность электрического поля и
индукция магнитного поля соответственно.
/Цитата 2/
Таким образом, появление магнитного
поля токов есть чисто релятивистский
эффект и никакой новой физической
субстанции (например, в виде магнитных
зарядов) появляться не должно, что и
подтверждается экспериментально
/Цитата 3/ В
результате магнитное поле можно
рассматривать как неизбежный релятивистский
результат движения электрич.
зарядов(тока
)
и нестационарности создаваемого ими
электрич.
поля (тока
смещения
В приведенных выше
цитатах, взятых из разных источников,
присутствует общая идея, которую можно
сформулировать так: «реальные» поля в
природе неизменно должны иметь
корпускулярный источник. Поля, не имеющие
такого источника суть эффекты или
процессы, происходящие в «реальных»
полях. Здесь под «реальными» понимаются
поля, признаваемые как самостоятельные
материальные сущности.
Видео:Смысл интеграла и производной. В помощь студентуСкачать

Изучение магнитного поля (закон Био-Савара-Лапласа)
Федеральное агентство
по образованию
Государственное образовательное
учреждение высшего профессионального
образования
Санкт-Петербургский государственный
горный институт им. Г.В. Плеханова
- (технический университет)
- Кафедра Общей и Технической физики
- Лабораторная работа №3
- Изучение
магнитного поля (закон Био-Савара-Лапласа)
ВЫПОЛНИЛА: ст. гр. ТНГ-10-1 /Бикбулатов Ф.Р./
ПРОВЕРИЛ: ассистент ______________ /Черняев А.В./
Цель
работы:Измерение магнитных полей, создаваемых проводниками различных конфигураций. Экспериментальная проверка закона Био-Савара-Лапласа.
Явление, изучаемое
в работе — магнитное поле.
Основные определения о понятия:
Магнитное поле – силовое поле в пространстве, окружающем токи и постоянные магниты. Создается только движущимися зарядами и действует только на движущиеся заряды.
- Соленоид – свернутый в спираль изолированный проводник, по которому течет электрический ток.
- Магнитная проницаемость
среды – безразмерная величина, показывающая во сколько раз магнитное поле макротоков усиливается за счет поля микротоков среды. - Электрический ток – направленное движение электрически заряженных частиц.
- Сила тока – скалярная физическая величина, равная величине электрического заряда, переносимого через поперечное сечение проводника за единицу времени.
- Индуктивность – величина, характеризующая магнитные свойства проводника.
- Магнитная индукция – основная характеристика магнитного поля, представляющая собой среднее значение суммарной напряженности микроскопических магнитных полей, созданных отдельными электронами и другими элементарными частицами.
Напряженность магнитного поля – векторная величина, являющаяся количественной характеристикой магнитного поля. Не зависит от магнитных свойств среды.
- Основные физические законы и соотношения:
- Закон Био-Савара-Лапласа:
- Определяет индукцию поля
создаваемого элементом проводника с током в точке, находящейся на расстоянии r от элемента проводника. - Магнитное поле на оси короткой катушки:
- В соответствии с принципом суперпозиции магнитное поле катушки представляет собой алгебраическую сумму полей отдельных витков.
- Циркуляции
вектора магнитной индукции: - Принцип суперпозиции магнитных полей:
- Магнитная индукция результирующего
поля, создаваемого несколькими потоками или движущимися зарядами, равна
векторной сумме магнитных индукций полей, создаваемых каждым током или движущимися зарядами в отдельности: - Правило правого
винта: - За положительное направление принимается направление поступательного движения винта, головка которого вращается в направлении тока, текущего в рамке.
- Схема установки:
- Принципиальная
электрическая схема установки - 1 – измеритель индукции
магнитного поля (тесламетр), А –
амперметр, 2 – соединительный провод, 3 – измерительный щуп, 4 – датчик
Холла, 5 – исследуемый объект (короткая катушка, прямой проводник, соленоид), 6 – источник тока, 7 – линейка для фиксирования положения датчика, 8 – держатель щупа. - Основные расчетные
формулы: - Магнитная индукция, создаваемая короткой катушкой:
- – радиус катушки, [
] — м - z – расстояние от центра катушки до датчика Холла, [z] — м
- – число витков катушки.
- – магнитная постоянная, [
] – Гн/м - – магнитная проницаемость среды
- – сила тока, [
] — А - – магнитная индукция, [
] — Тл - Магнитная индукция, создаваемая соленоидом:
- — длина соленоида, [
] — м - — число витков соленоида
- – магнитная постоянная, [
] – Гн/м - – магнитная проницаемость
среды - – сила тока, [
] — А - – магнитная индукция, [
] — Тл - Кратчайшее
расстояние от датчика до проводника с током: - Индуктивность соленоида:
- Y – потокосцепление
- Потокосцепление:
- Площадь сечения
соленоида: - Погрешности прямых измерений:
- ∆I=5∙10-2 (A)
- ∆R=0,5∙10-3(Ом)
- ∆l=0,5∙10-3(м)
- ∆z=0,5∙10-3(м)
- ∆B=0,01(мТл)
- Формулы погрешности
косвенных измерений: - Максимальная абсолютная погрешность измерения магнитной
индукции, создаваемой короткой катушкой: - Максимальная абсолютная погрешность измерения магнитной
индукцией, создаваемой соленоидом: - Максимальная относительная
погрешность измерения кратчайшего
расстояния от датчика Холла до проводника с током: - Максимальная относительная
погрешность измерения индуктивности соленоида: - Максимальная относительная
погрешность измерения потокосцепления: - Максимальная относительная
погрешность измерения площади
сечения соленоида: - Таблицы измерений:
Измерение зависимости
магнитной индукции на оси короткой катушки от расстояния до центра катушки.
| см | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | ||
| мТл | 0,01 | 0,03 | 0,04 | 0,05 | 0,08 | 0,13 | 0,21 | 0,28 | ||
| Bтеор | мТл | 0,03 | 0,04 | 0,05 | 0,08 | 0,11 | 0,16 | 0,23 | 0,29 | 0,32 |
| см | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| мТл | 0,27 | 0,24 | 0,17 | 0,11 | 0,06 | 0,03 | 0,01 | ||
| Bтеор | мТл | 0,29 | 0,23 | 0,16 | 0,11 | 0,08 | 0,05 | 0,04 | 0,03 |
Измерение магнитной
индукции в центре короткой катушки
от силы тока в ней.
| A | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | |
| мТл | 0,03 | 0,06 | 0,08 | 0,12 | 0,14 | 0,17 | 0,2 | |
| Bтеор | мТл | 0,03 | 0,06 | 0,09 | 0,13 | 0,16 | 0,19 | 0,22 |
| A | 4 | 4,5 | 5 | |
| мТл | 0,23 | 0,26 | 0,29 | |
| Bтеор | мТл | 0,25 | 0,28 | 0,32 |
Измерение зависимости
магнитной индукции на оси соленоида
от расстояния до его центра.
| см | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | ||
| мТл | 0,34 | 0,95 | 1,92 | 2,42 | 2,6 | 2,63 | 2,69 | 2,7 | 2,71 | 2,72 | 2,73 | |
| Bтеор | мТл | 0,53 | 1,18 | 2,95 | 2,95 | 2,95 | 2,95 | 2,95 | 2,95 | 2,95 | 2,95 | 2,95 |
| см | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| мТл | 2,71 | 2,68 | 2,65 | 2,63 | 2,61 | 2,54 | 2,37 | 1,83 | 0,87 | 0,3 | |
| Bтеор | мТл | 2,95 | 2,95 | 2,95 | 2,95 | 2,95 | 2,95 | 2,95 | 2,95 | 1,18 | 0,53 |
Измерение магнитной
индукции в центре соленоида от силы тока в нем.
| A | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | |
| мТл | 0,25 | 0,53 | 0,8 | 1,09 | 1,37 | 1,68 | 1,91 | 2,2 | 2,45 | 2,74 | |
| Bтеор | мТл | 0,25 | 0,50 | 0,75 | 0,99 | 1,24 | 1,49 | 1,74 | 1,99 | 2,24 | 2,49 |
| мкГн | 24 |
Измерение магнитной
индукции, создаваемой прямолинейным
проводником от силы тока в нем.
🌟 Видео
Дивергенция векторного поляСкачать

Как использовать интеграл в обычной жизни. Математик МГУ и Савватеев #shortsСкачать

Дивергенция и ротор: Язык уравнений Максвелла, течения жидкости и большеСкачать

Урок 9. Проекции вектора на координатные осиСкачать

Формула Стокса, ротор и его физический смыслСкачать

Лекция 2.3. Теорема о циркуляцииСкачать
























































 — магнитная постоянная;
— магнитная постоянная;













