Докажите что если у четырехугольника есть ось симметрии то это ромб

Четырёхугольник имеет ровно две оси симметрии. Верно ли, что он — либо прямоугольник, либо ромб?

Решение:
Если фигура имеет ровно две оси симметрии, то они взаимно перпендикулярны. Действительно, пусть l₁ и l₂ — оси симметрии фигуры. Предположим, что они не перпендикулярны. Тогда прямая, симметричная l₂ относительно l₁, — также ось симметрии, не совпадающая ни с l₁, ни с l₂. Получили противоречие.

Докажем теперь, что если фигура имеет две взаимно перпендикулярные оси симметрии, то она имеет центр симметрии. Примем оси симметрии за оси координат OX и OY. Тогда, если точка (x;y) принадлежит фигуре, то ей также принадлежат точки (- x;y) (симметрия относительно оси OY) и (- x; — y) (симметрия относительно OX). Значит, точка (- x; — y), симметричная точке (x;y) относительно начала координат, принадлежит фигуре. Следовательно, фигура симметрична относительно начала координат.

Четырёхугольник, имеющий центр симметрии, — параллелограмм. Его оси симметрии взаимно перпендикулярны и являются либо диагоналями, либо серединными перпендикулярами к сторонам. Следовательно, четырёхугольник является либо ромбом, либо прямоугольником.

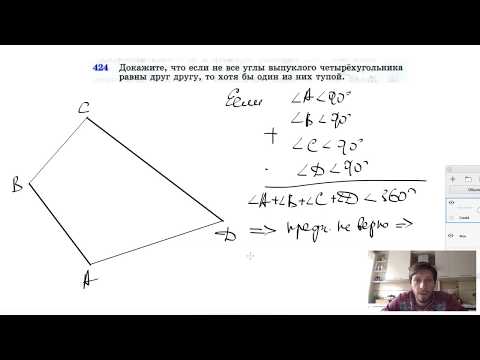
Видео:№424. Докажите, что если не все углы выпуклого четырехугольника равны друг другуСкачать

Презентация по математике «Подготовка к ЕГЭ» Задача 8.

Видео:№441. Докажите, что прямые, содержащие диагонали ромба, являются его осями симметрии.Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:Ось симметрииСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Индивидуально-групповые занятия в 11 классе ПОДГОТОВКА К ЕГЭ ПО МАТЕМАТИКЕ МБОУ Крюковская СОШ Учитель математики Угроватова Татьяна Викторовна

Центральная симметрия. Симметрия относительно точки или центральная симметрия — это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону центра симметрии, соответствует другая точка, расположенная по другую сторону центра. При этом точки находятся на отрезке прямой, проходящей через центр, делящий отрезок пополам. А О В

Осевая симметрия. Симметрия относительно прямой (или осевая симметрия) — это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону прямой, всегда будет соответствовать точка, расположенная по другую сторону прямой, а отрезки, соединяющие эти точки, будут перпендикулярны оси симметрии и делятся ею пополам. a А В

Зеркальная симметрия Точки А и В называются симметричными относительно плоскости α (плоскость симметрии), если плоскость α проходит через середину отрезка АВ и перпендикулярна к этому отрезку. Каждая точка плоскости α считается симметричной сама себе. А В α

Как прекрасен этот мир! Рис. 1 Рис. 2 Рис. 3 Рис. 4 Рис. 5 Рис. 6 Рис. 7

Симметричный алфавит (творческие работы учащихся) Рис. 11 Рис. 12 Рис. 13

Тест. 1 вариант 2 вариант 1. Не имеет оси симметрии. окружность; угол; параллелограмм. 1. Какая фигура не имеет центра симметрии? отрезок; луч; пара пересекающихся прямых.

2. Две оси симметрии имеет. равнобедренный треугольник; равнобедренная трапеция; ромб. 2. Какое утверждение неверное? Если треугольник имеет ось симметрии, то он равнобедренный. Если треугольник имеет две оси симметрии, то он равносторонний. В равностороннем треугольнике две оси симметрии.

3. Какое утверждение верное? В параллелограмме точка пересечения диагоналей является центром симметрии. В равнобедренной трапеции точка пересечения диагоналей является ее центром симметрии. В равностороннем треугольнике точка пересечения медиан является центром его симметрии. 3. Имеет четыре оси симметрии. прямоугольник; ромб; квадрат.

4. Из того, что точки О и А симметричны относительно точки В, не следует, что. АО = 2ОВ; ОВ = 2АО; ОВ = АВ. 4. Точки А и В симметричны относительно прямой а, если они. лежат на перпендикуляре к прямой а; равноудалены от прямой а; лежат на перпендикуляре к прямой а и равноудалены от нее.

5. Диагональ АС четырехугольника АВСО является его осью симметрии. Этот четырехугольник не может быть. параллелограммом; ромбом; квадратом. 5. Из того, что точки М и N симметричны относительно точки К, следует, что. МК = 0,5 КN; МN=2МК; NК = 2МN.

6.ВD — высота в равнобедренном треугольнике АВС. Какое утверждение неверное? ВD — ось симметрии треугольника АВС. Точки А и С симметричны относительно точки D. Точка D — центр симметрии треугольника АВС. 6. Диагональ МР выпуклого четырехугольника МNРК является его осью симметрии. Этот четырехугольник не может быть. прямоугольником; ромбом; квадратом.

7. Прямая а делит отрезок АВ пополам. Какое утверждение верное? Точки А и В симметричны относительно прямой а. Точки А и В симметричны относительно точки пересечения прямой а и отрезка АВ. В данном случае нет ни осевой, ни центральной симметрии. 7. Прямая, проходящая через середину одной из сторон параллелограмма, является его осью симметрии. Тогда этот параллелограмм не может быть. прямоугольником; ромбом; квадратом.

8. Среди точек А (3; — 4), В (- 3; — 4), С (- 3; 4) укажите пару, симметричную относительно начала координат: А и В; В и С; А и С. 8. Среди точек D (4; — 7), К (- 4; 7), Р (- 4; — 7) укажите пару, симметричную относительно оси абсцисс: К и D; К и Р; Р и D.

9. Для прямой у = х + 2 укажите прямую, симметричную относительно оси ОY. у = -х + 2; у = х — 2; у = -х — 2. 9. Для прямой у = х + 2 укажите прямую, симметричную относительно начала координат: у = -х + 2; у = х — 2; у = -х — 2.

Ответы: 1 2 3 4 5 6 7 8 9 1в c c a b a c b c a 2в b c c c b a b b b

Мауриц Эшера (1898г.-1972г.) Художник-график (Нидерланды) Рис. 14 Рис. 15

Рис. 16, 17 Рис. 18, 19

Элементы симметрии правильных многогранников. Правильный многогранник Центр Ось Плоскость Тетраэдр Октаэдр Икосаэдр Гексаэдр Додекаэдр

Элементы симметрии правильных многогранников Правильный многогранник Центр Ось Плоскость Тетраэдр ___ 3 6 Октаэдр 1 9 9 Икосаэдр 1 15 15 Гексаэдр 1 9 9 Додекаэдр 1 15 15

Пример к таблице Октаэдр Рис. 20 Рис. 21

Пример к таблице Додекаэдр Рис. 22 Рис. 23

Домашнее задание 1.Достройте, применив осевую симметрию. Рис. 24

Домашнее задание. 2. Постройте фигуру, симметричную данной относительно: а) точки б) прямой Рис. 25 Рис. 26

Домашнее задание 3. Творческое: «В мире животных». Нарисуйте представителя из мира животных и покажите ось симметрии. Примеры: Рис. 27, 28

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 975 человек из 79 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 701 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 337 человек из 71 региона

Ищем педагогов в команду «Инфоурок»

• Угроватова Татьяна ВикторовнаНаписать 1017 15.06.2017

Номер материала: ДБ-557916

15.06.2017 375

15.06.2017 161

15.06.2017 384

15.06.2017 777

15.06.2017 178

15.06.2017 1456

15.06.2017 159

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения готовит рекомендации по построению «идеальной школы»

Время чтения: 1 минута

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:№444* Докажите, что если фигура имеет две взаимно перпендикулярные оси симметрии, то точка ихСкачать

Урок геометрии в 8 классе по теме «Осевая симметрия» в технологии деятельностного подхода

Урок геометрии в 8 классе

по теме «Осевая симметрия»

в технологии деятельностного подхода

МАОУ «СОШ №16» г. Перми

1 этап Самоопределение к деятельности (1-2 мин)

Ежедневно каждый из нас по несколько раз в день видит свое отражение в зеркале. Это настолько обычно, что мы не удивляемся, не задаем вопросов и вообще не обращаем внимания на зеркало и прочие пустяки. И только философы и математики не теряют способности удивляться. Сейчас мы совершим путешествие по страницам одной из самых любимых детьми и взрослыми сказок, которую написал более ста лет назад английский математик Льюис Кэролл. Благодаря зеркалу мы сможем увидеть то, что просто глазами увидеть нельзя.

На этом рисунке изображена девочка, любующаяся рыбкой. Найдите здесь еще осьминога и бабочку. Если поставить волшебное зеркало вдоль вертикальной черты, перпендикулярно плоскости листа, то увидим осьминога, сидящего на камне. А чтобы найти бабочку, нужно поставить зеркало вдоль наклонной черты, тоже перпендикулярно листу. А теперь попробуйте сами.

Учащиеся работают по книге «Волшебное зеркало» Оксаны Демченко.

Каждому столу дается по рисунку. С помощью зеркала выполните задание под рисунком.

1)Найти зонтик, который Алиса прихватила с собой.

2)Найди лицо королевы.

3)Как гусеница превращается в бабочку?

2этап Актуализация знаний и фиксация затруднения в деятельности (5-6 мин)

Что же меняется в предмете при его отображении в зеркале? Проведем опыты с зеркалами. Постарайтесь подметить особенности зеркального отображения и сделать из каждого опыта выводы. Выводы запишите в тетрадь.

1)Напишите свое имя печатными буквами в столбик и посмотрите на его отображение в зеркале. Поворачивает ли зеркало ваше имя? (имя в зеркале тоже написано сверху вниз)

2)Чем отличаются записи МАША и ЮРА? Полоски с именами расположите параллельно поверхности зеркала (буквы пишу слева направо, а в зеркале каждая буква написана справа налево)

3)На полоску бумаги горизонтально печатными буквами написаны слова ЧАЙ и КОФЕ. Положите эту полоску перед зеркалом на стол. Почему зеркало не перевернуло слово КОФЕ и до неузнаваемости изменило слово ЧАЙ? (слово не меняется, если каждая буква симметрична относительно вертикальной прямой)

3 Этап (Постановка учебной задачи (2-3 мин)

Имеет ли выполненное задание имеет связь с геометрией и темой предыдущего урока?

Что мы знаем про четырехугольники (свойства на ватмане)

Рассмотрим четырехугольники с помощью зеркала

Посмотреть: изображается ли точно половинка четырехугольника:

Какие выводы у вас получились?

Значит, зеркало нам показывало симметрию.

Насколько важно знать законы симметрии?

4 этап.Построение выхода из затруднения(10-11 мин)

Проверим ваши предположения с помощью моделей четырехугольников, но уже без зеркала. Работа с моделями.

Постройте точку А1 симметричную точке А относительно оси L

Опорная схема на альбомном листе

В тетради для каждого четырехугольника построить оси симметрии

Вывод (сколько у каждого четырехугольника осей симметрии)

Сравните параллелограмм и трапецию.

5 этап Первичное закрепление во внешней речи (4-5 мин)

Исследование: постройте фигуру с двумя осями симметрии при разных значениях угла между осями

3) прямой угол – Выход на центральную симметрию

Вывод — центральная симметрия

Правило построения центральной симметрии ( на ватмане)

Пример: Постройте точку В и симметричную ей точку В1.

6 этап Самостоятельная работа с проверкой( 4-5 мин)

1. Сколько осей симметрии имеет:

2. Какая из этих букв имеет ось симметрии:

А, Б, Г, Е, О, Р (А, Е, О)

3. Построить точку, симметричную точке М относительно середины отрезка АВ.

2.Постройте треугольник АВС, симметричный относительно прямой l треугольнику АВС

3.Докажите что точка пересечения диагоналей параллелограмма является центром симметрии

7 этап Включение в систему знаний и повторение ( 4-5 мин)

1.Докажите, что если четырёхугольник имеет ровно две оси симметрии, то он является ромбом или прямоугольником, а если 4 – то это квадрат. 2.Докажите, что четырёхугольник не может иметь ровно 3 или больше 4 осей симметрии.

8 этап Рефлексия деятельности (2-3 мин)

Итог урока. Цель. Тема. Домашнее задание.(по выбору)

1.Докажите что диагонали ромба являются осями симметрии. Сколько осей симметрии может иметь n-угольник при n = 3, 5, 6?

2.Сколько вершин может быть у многоугольника, имеющего n осей симметрии? Как могут быть расположены его вершины относительно осей?

3.Роль симметрии и асимметрии в окружающем мире и на других уроках.

«Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия так приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем оно основано? Разве во всем в жизни симметрия?»

1.Работа с зеркалом

1)Напишите свое имя печатными буквами в столбик и посмотрите на его отображение в зеркале. Поворачивает ли зеркало ваше имя?

2)Чем отличаются записи МАША и ЮРА? Полоски с именами расположите параллельно поверхности зеркала.

3)На полоску бумаги горизонтально печатными буквами написаны слова ЧАЙ и КОФЕ. Положите эту полоску перед зеркалом на стол. Почему зеркало не перевернуло слово КОФЕ и до неузнаваемости изменило слово ЧАЙ?

2. Самостоятельная работа

1. Сколько осей симметрии имеет:

2. Какая из этих букв имеет ось симметрии:

3. Построить точку, симметричную точке М относительно середины отрезка АВ.

2.Постройте треугольник А1В1С1 симметричный треугольнику АВС относительно прямой а

3.Докажите, что точка пересечения диагоналей параллелограмма является центром симметрии.

1.Докажите, что если четырёхугольник имеет ровно две оси симметрии, то он является ромбом или прямоугольником, а если 4 – то это квадрат.

2.Докажите, что четырёхугольник не может иметь ровно 3 или больше 4 осей

Тема « Свойства осевой симметрии»

Цель: Создание условий для моделирования учащимися свойств осевой симметрии

Задачи: — актуализировать знания учащихся о симметрии

-мотивировать интерес к симметрии как к жизненному явлению

-развивать умение решать задачи на основе свойств симметрии

-развивать коммуникативные способности

-научить применять свойства осевой симметрии в практике

Соответствие принципам деятельностного подхода на уроке

1.Работа с зеркалом

2.Работа с моделями 3.моделирование

2.Новый способ действий

5.Тренировка по алгоритму

6.Планы на будущее

7.Применение полученных знаний в решении задач

Целостное представление о мире

1.Связь с литературой и жизнью

2.Взаимосвязь отдельных курсов математики

1.Самостоятельная работа 1-3 задания по минимуму, 1-5 по максимуму;

2.Моделирование на доске по максимуму, в тетради – по минимуму

5.Работа с зеркалом и моделями

1.Изменение форм работы (индивидуальная, в парах, устная, письменная, практическая 2.Задания на выбор в самостоятельной и домашней работе

1.Новый способ определения центральной симметрии

3.Решение геометрической задачи комбинаторным способом

🌟 Видео

8 класс, 3 урок, ЧетырехугольникСкачать

Прямоугольник. Ось симметрии. 5 классСкачать

Осевая симметрия. 6 класс.Скачать

8 класс, 9 урок, Осевая и центральная симметрияСкачать

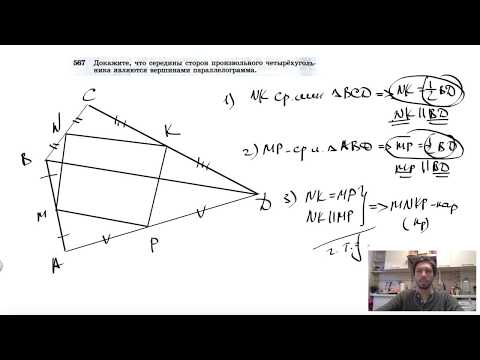
№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать

8 класс, 8 урок, Ромб и квадратСкачать

Многоугольники. Ось симметрииСкачать

№409. Докажите, что ромб, у которого один угол прямой, является квадратом.Скачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Задача, которую боятсяСкачать

№433. Из вершины В ромба ABCD проведены перпендикуляры ВК и ВМ к прямым AD и DC. Докажите, что лучСкачать

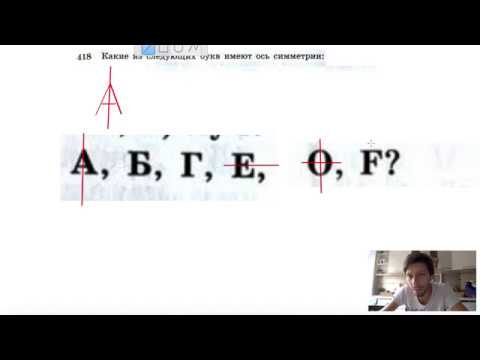
№418. Какие из следующих букв имеют ось симметрии: А, Б, Г, Е, О, F?Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Математика 5 класс. Ось симметрии фигурыСкачать

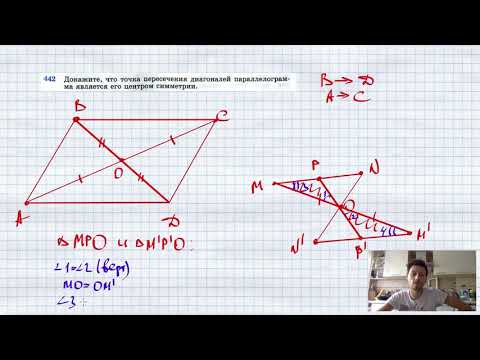
№442. Докажите, что точка пересечения диагоналей параллелограмма является его центром симметрии.Скачать

Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать