Прямая dd1 и плоскость abb1 прямая параллельна плоскости

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8

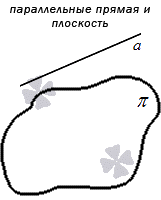
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек (а || )

Признак параллельности прямой и плоскости.

Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.

Определи взаимное расположение данной прямой и плоскости.

Прямая DD1 и плоскость (ADD1):

Прямая LP и плоскость (CDD1):

Прямая XY и плоскость (ABC):

Прямая DC и плоскость (AA1B):

Прямая MS и плоскость (ABB1):

Точки M, N, P и Q являются соответственно серединами отрезков AD, CD, BC и AB.

Вычислите периметр четырёхугольника MNPQ, если AC= 11 см и BD= 17 см.

Ответ: периметр четырехугольника MNPQ равен см.

Трапеция ABCD, основание BC которой равно 24cм, лежит в плоскости б. Точка M не находится в плоскости трапеции. Точка Kделит отрезок MB так, чтоMK:KB=1:4. Плоскость ADK пересекает отрезок MC в некоторой точке N. Определи длину отрезка KN.

1. Назови пучок параллельных прямых: ∥

∥

2. Назови подобные треугольники: ДKMN

Д

3. KN= (округли до одной десятой).

Задание №4. С учебника

Домашняя работа: С учебника

Когда называются прямая и плоскость прямыми? Назовите случаи взаимного расположения прямой и плоскости. Признак параллельности прямой и плоскости.

Задание СРС: Определите взаимное расположение стороны октаэдра.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Контрольная работа по геометрии для студентов 1 курса (СПО) по теме параллельность и перпендикулярность в пространстве.

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

ГАОУ СПО Архангельской области «КИТ»

Контрольная работа по геометрии для студентов 1 курса (СПО)

по теме параллельность и перпендикулярность в пространстве.

Подготовила: Налетова Ирина Александровна,

г. Коряжма — 2014

Учебник, по которому ведется преподавание

Геометрия, 10–11: Учебник для общеобразовательных учреждений.Л.С. Атанасян, Просвещение, 2010. Математика сборник заданий для проведения письменного экзамена за курс средней школы 11 класс. Г.В.Дорофеев. Дрофа. Москва 2002

Параллельность и перпендикулярность в пространстве

Форма и методы контроля

1) по степени индивидуализации (индивидуальный);

2) по манере исполнения (письменный);

3) по способу подачи контролирующих заданий (контрольная работа)

Преподавателю определить качество усвоения учебного материала, уровня овладения знаниями, умениями и навыками, предусмотренными учебной программой по математике.

Обучающемуся привести в систему усвоенный за определенное время учебный материал

Варианты имеют одинаковый уровень сложности и содержат 20 заданий с выбором ответа, каждое из которых оценивается 1б, 7 заданий с кратким ответом, каждое из которых оценивается 2б, 4 задания с развёрнутым ответом, каждое из которых оценивается 3б. Данная работа позволяет в полной мере оценить объём и качество усвоенного материала. Может использоваться в старшей школе

Отметка «5» выставляется, если студент набрал 37 – 46 баллов.

Отметка «4» выставляется, если студент набрал 27 – 36 балл.

Отметка «3» выставляется, если студент набрал 19 – 26 баллов.

Отметка «2» выставляется, если студент набрал менее 19 баллов.

Контрольная работа по стереометрии

Параллельность прямых и плоскостей в пространстве Часть 1. Задание с выбором ответа (1 балл).

Какой плоскости не принадлежит точка А?

А) Р D В В) А D С

На каких плоскостях лежит прямая DB ?

В какой точке пересекаются прямая PC и плоскость ADB ?

По какой прямой пересекаются плоскости A ВС и ADC ?

Какие прямые лежат в плоскости BDC ?

А) DB , AC , DK . AB

В) KB , DA , DK . CP

С) DP , DC , DK . CA

Д) DB , DC , DK . CB

Укажите точку пересечения прямой MD с плоскостью ABC

Укажите прямую пересечения плоскостей АВС и АВВ₁

Плоскости α и β пересекаются по прямой с. Выберите верную запись:

А) α × β= с В) α ∩ β= с

С) α ║ β= с Д) α ∩ β= С

Туго натянутая нить закреплена в точках 1,2,3,4,5, расположенных на стержнях SA , SB , SC . Укажите количество точек в которых отрезки нити соприкасаются

Как располагаются прямые AD ₁ и D ₁ C ₁?

Найдите угол между прямыми AD ₁ и ВВ₁

Найдите точку пересечения прямых DC и CC ₁

Найдите рёбра, параллельные грани АВВ₁А₁

С) DD ₁ , CC ₁ , C ₁ D _1, D С

Перпендикулярность прямых и плоскостей в пространстве Часть 1. Задание с выбором ответа (1 балл).

Укажите рёбра, перпендикулярные плоскости АВВ₁

А) D А, В C ,СС₁. AB

Выберите верное утверждение

А) AD ║ BA В) AB D ₁ С ₁

С) DC ║ BC Д) D С BC

Как расположены друг к другу рёбра куба, выходящие из одной вершины?

Отрезок В D перпендикулярен плоскости α. С D является::

С) Проекцией наклонной

Укажите общий перпендикуляр для прямых AD и CC ₁

Плоскости α и β параллельны. Каково взаимное расположение прямых AD и BC ?

Прямые a и b параллельные и лежат в плоскости α. Через каждую из этих прямых проведена плоскость, перпендикулярная α . Каково взаимное расположение полученных плоскостей?

А) Пересекаются В) Скрещиваются

С) Параллельны Д) Совпадают

Часть 2. Задание с развёрнутым ответом (2 балла).

Через концы отрезка MN и его середину К проведены параллельные прямые, пересекающие плоскость α в точках M _1, , N ₁ и К₁ . Найдите длину отрезка КК₁ , если отрезок MN не пересекает α и ММ₁ = 6 см, NN ₁= 2 см.

Даны две параллельные плоскости. Через точки А и В одной из плоскостей проведены две параллельные прямые до пересечения в точках А₁ и В₁. Найдите длину отрезка А₁ В₁ если АВ = 10 см.

Из точки М проведены к плоскости α до пересечения в точках N и К два отрезка. Точки D и Е – середины отрезков MN и МК. Найдите длину отрезка N К, если D Е = 4 см.

Через вершину острого угла прямоугольного треугольника АВС с прямым углом С проведена прямая А D , перпендикулярная плоскости треугольника. Чему равно расстояние от точки D до вершины С, если АС = 6 см; А D = 8 см.

Наклонная равна 2 см. Чему равна проекция этой наклонной на плоскость, если наклонная составляет с плоскостью угол равный 45 º?

Отрезки двух наклонных, проведённые из одной точки до пересечения с плоскостью, равны 15 и 20 см, проекция одного из отрезков равна 16 см. Найдите проекцию другого отрезка.

Чему равен угол между плоскостью А₁В₁С₁ D ₁ и плоскостью проходящей через прямые А₁В₁ и С D

Часть 3. Задание с развёрнутым ответом (3 балла).

Из точки А к плоскости α проведены два отрезка АС и АВ . Точка D принадлежит АВ, точка Е принадлежит АС. D Е параллельна α и равна 5 см. Найти длину отрезка ВС, если .

Из точки О пересечения диагоналей квадрата АВС D к е го плоскости восстановлен перпендикуляр ОМ так, что . Найдите косинус угла АВМ.

Из точки А построены три взаимоперпендикулярных отрезка АВ, АС и AD . Найдите длину отрезка С D если АС = а, ВС = в, В D = с

В кубе со стороной а найдите расстояние между прямыми В D ₁ и СС₁.

Контрольная работа по стереометрии

Параллельность прямых и плоскостей в пространстве Часть 1. Задание с выбором ответа (1 балл).

Какой плоскости не принадлежит точка В?

А) Р D В В) А D С

На каких плоскостях лежит прямая D А?

В какой точке пересекаются прямая D К и плоскость ADB ?

По какой прямой пересекаются плоскости A ВС и AD В?

Какие прямые лежат в плоскости BD А?

А) DB , AC , DK . AB

В) KB , DA , DK . CP

С) DP , D В, D А. В A

Д) DB , DC , DK . CB

Укажите точку пересечения прямой NC ₁ с плоскостью A ₁ B ₁ C ₁

Укажите прямую пересечения плоскостей АВ D и А DD ₁

Прямые а и b пересекаются в точке С. Выберите верную запись:

А) a × b = с В) a ∩ b = с

С) a ║ b = с Д) a ∩ b = С

Туго натянутая нить закреплена в точках 1,2,3,4,5, 6 расположенных на стержнях SA , SB , SC . Укажите количество точек в которых отрезки нити соприкасаются

Как располагаются прямые DD ₁ и DC ?

Найдите угол между прямыми A А₁ и ВС

Найдите точку пересечения прямых DC и D ₁ P

Найдите рёбра, параллельные грани А DD ₁А₁

С) А D , В C , A ₁ D _1, АС

Перпендикулярность прямых и плоскостей в пространстве Часть 1. Задание с выбором ответа (1 балл).

Укажите рёбра, перпендикулярные плоскости АВС

А) D А, В C ,СС₁. AB

Выберите верное утверждение

А) AD BA В) AB D ₁ С ₁

С) DC ║ B В ₁ Д) D С BC

Можно ли провести плоскость через четыре произвольные точки пространства?

Отрезок В D перпендикулярен плоскости α. СВ является::

С) Проекцией наклонной

Укажите общий перпендикуляр для прямых A В и CC ₁

Плоскости α и β параллельны. Каково взаимное расположение прямых A С и BD ?

Прямые a и b -скрещивающиеся.Через а проведена плоскость α ║ b ,. Через прямую b проведена плоскость β║а, . Каково взаимное расположение плоскостей α и β?

А) Пересекаются В) Скрещиваются

С) Параллельны Д) Совпадают

Часть 2. Задание с развёрнутым ответом (2 балла).

Через концы отрезка MN и его середину К проведены параллельные прямые, пересекающие плоскость α в точках M _1, , N ₁ и К₁ . Найдите длину отрезка КК₁ , если отрезок MN не пересекает α и ММ₁ = 12см, NN ₁= 4 см.

Даны две параллельные плоскости. Через точки А и В одной из плоскостей проведены две параллельные прямые до пересечения в точках А₁ и В₁. Найдите длину отрезка АА₁ если ВВ₁ = 16 см.

Из точки М проведены к плоскости α до пересечения в точках N и К два отрезка. Точки D и Е – середины отрезков MN и МК. Найдите длину отрезка D Е , если N К = 4 см.

Через вершину острого угла прямоугольного треугольника АВС с прямым углом С проведена прямая А D , перпендикулярная плоскости треугольника. Чему равно расстояние от точки D до вершины С, если АС = 3 см; А D = 4 см.

Наклонная равна 2 см. Чему равна проекция этой наклонной на плоскость, если наклонная составляет с плоскостью угол равный 60 º?

Отрезки двух наклонных, проведённые из одной точки до пересечения с плоскостью, равны 7 и 10 см, проекция одного из отрезков равна 8 см. Найдите проекцию другого отрезка.

Чему равен угол между плоскостью А₁В₁С₁ D ₁ и плоскостью проходящей через прямые АВ и С₁ D ₁

Часть 3. Задание с развёрнутым ответом (3 балла).

Из точки А к плоскости α проведены два отрезка АС и АВ . Точка D принадлежит АВ, точка Е принадлежит АС. D Е параллельна α и равна 5 см. Найти длину отрезка ВС, если .

Из точки О пересечения диагоналей квадрата АВС D к е го плоскости восстановлен перпендикуляр ОМ так, что . Найдите косинус угла АВМ.

Из точки А построены три взаимоперпендикулярных отрезка АВ, АС и AD . Найдите длину отрезка В D если АС = а, ВС = в, С D = с

В кубе со стороной а найдите расстояние между прямыми В₁ D и АА₁.

Контрольная работа по стереометрии

Параллельность прямых и плоскостей в пространстве Часть 1. Задание с выбором ответа (1 балл).

Какой плоскости не принадлежит точка С?

А) Р D В В) А D С

На каких плоскостях лежит прямая D С?

В какой точке пересекаются прямая D М и плоскость A С B ?

По какой прямой пересекаются плоскости A ВС и В DC ?

Какие прямые лежат в плоскости B А C ?

А) А B , AC ,СР. С B

В) KB , DA , DK . CP

С) DP , DC , DK . CA

Укажите точку пересечения прямой NA ₁ с плоскостью A ₁ C ₁ D ₁

Укажите прямую пересечения плоскостей АВС и D СС₁

Плоскости α и β пересекаются по прямой b . Выберите верную запись:

А) α × β= b В) α ∩ β= B

С) α ║ β= b Д) α ∩ β= b

Туго натянутая нить закреплена в точках 1,2,3,4,5, 6 расположенных на стержнях a , b , c . Укажите количество точек в которых отрезки нити соприкасаются

Как располагаются прямые BP и D ₁ C ₁?

Найдите угол между прямыми AD ₁ и А ₁В₁

Найдите точку пересечения прямых D А и АА₁

Найдите рёбра, параллельные грани АВС D

С) А ₁В₁, В ₁ C ₁, A ₁ D _1, D ₁С ₁

Перпендикулярность прямых и плоскостей в пространстве Часть 1. Задание с выбором ответа (1 балл).

Укажите рёбра, перпендикулярные плоскости С DD ₁

А) D А, В C ,СС₁. AB

Выберите верное утверждение

А) AD ║ DC В) AB D ₁ С ₁

С) DC ║ BC Д) D С DD ₁

Две точки круга лежат в плоскости. Лежит ли весь круг в этой плоскости?

Отрезок В D перпендикулярен плоскости α. В D является::

С) Проекцией наклонной

Укажите общий перпендикуляр для прямых С D и ВВ₁

Отрезки АВ и С D лежат в плоскостях α и β. Прямые АС и В D параллельны. Каково взаимное расположение плоскостей α и β?

Три луча АВ, АС, АК попарно перпендикулярны. Как расположен каждый из лучей по отношению плоскости, определяемой двумя другими лучами.

А) Перпендикулярен В) Скрещивается

С) Параллелен Д) Совпадает

Часть 2. Задание с развёрнутым ответом (2 балла).

Через концы отрезка MN и его середину К проведены параллельные прямые, пересекающие плоскость α в точках M _1, , N ₁ и К₁ . Найдите длину отрезка NN ₁ , если отрезок MN не пересекает α и ММ₁ = 6 см, KK ₁= 4 см.

Даны две параллельные плоскости. Через точки А и В одной из плоскостей проведены две параллельные прямые до пересечения в точках А₁ и В₁. Найдите длину отрезка АВ если А₁ В₁ = 3 см.

Из точки М проведены к плоскости α до пересечения в точках N и К два отрезка. Точки D и Е – середины отрезков MN и МК. Найдите длину отрезка D Е, если N К = 12см.

Через вершину острого угла прямоугольного треугольника АВС с прямым углом С проведена прямая А D , перпендикулярная плоскости треугольника. Чему равно расстояние от точки D до вершины С, если АС = 12 см; А D = 16 см.

Наклонная равна 2 см. Чему равна проекция этой наклонной на плоскость, если наклонная составляет с плоскостью угол равный 30 º?

Отрезки двух наклонных, проведённые из одной точки до пересечения с плоскостью, равны 4 и 5 см, проекция одного из отрезков равна 4 см. Найдите проекцию другого отрезка.

Чему равен угол между плоскостью А₁В₁С₁ D ₁ и плоскостью проходящей через прямые А₁ D ₁ и СВ

Часть 3. Задание с развёрнутым ответом (3 балла).

Из точки А к плоскости α проведены два отрезка АС и АВ . Точка D принадлежит АВ, точка Е принадлежит АС. D Е параллельна α и равна 12 см. Найти длину отрезка ВС, если .

Из точки О пересечения диагоналей квадрата АВС D к е го плоскости восстановлен перпендикуляр ОМ так, что . Найдите косинус угла АВМ.

Из точки А построены три взаимоперпендикулярных отрезка АВ, АС и AD . Найдите длину отрезка С D если АС = 3 см, ВС = 4 см,

В кубе со стороной а найдите расстояние между прямыми D В₁ и СС₁.

Контрольная работа по стереометрии

Параллельность прямых и плоскостей в пространстве Часть 1. Задание с выбором ответа (1 балл).

Какой плоскости не принадлежит точка D ?

А) Р D В В) А D С

На каких плоскостях лежит прямая С B ?

В какой точке пересекаются прямая DM и плоскость ADB ?

По какой прямой пересекаются плоскости A ВС и PDC ?

Какие прямые лежат в плоскости PDC ?

А) DB , AC , DK . AB

В) KB , DA , DK . CP

С) DP , DC , DM . CP

Д) DB , DC , DK . CB

Укажите точку пересечения прямой NC с плоскостью ABD

Укажите прямую пересечения плоскостей АВС и CDD ₁

Плоскости α и β пересекаются по прямой с. Выберите верную запись:

А) α × β= с В) α ∩ β= с

С) α ║ β= с Д) α ∩ β= С

Туго натянутая нить закреплена в точках 1,2,3,4,5, 6 расположенных на стержнях a , b , c . d Укажите количество точек в которых отрезки нити соприкасаются

А) 0 В) 1 С) 2 Д) 3

Как располагаются прямые DD ₁ и AA ₁?

Найдите угол между прямыми AD и DC

Найдите точку пересечения прямых AB и AD ₁

Найдите рёбра, параллельные грани DCC ₁ D ₁

С) А D , В C , A ₁ D _1, D С

Перпендикулярность прямых и плоскостей в пространстве Часть 1. Задание с выбором ответа (1 балл).

Укажите рёбра, перпендикулярные плоскости А DD ₁

А) D А, В C ,СС₁. AB

Выберите верное утверждение

А) AD ║ BC В) AB D ₁ С ₁

С) DC ║ BC Д) D С BA

Две точки треугольника лежат в плоскости. Лежит ли весь треугольник в этой плоскости?

Отрезок В D перпендикулярен плоскости α. С D является::

С) Проекцией наклонной

Укажите общий перпендикуляр для прямых B С и DD ₁

Плоскости α и β параллельны. Каково взаимное расположение прямых AB и CD ?

Прямые a и b -скрещивающиеся.Через а проведена плоскость α ║ b ,. Через прямую b проведена плоскость β║а, . Каково взаимное расположение плоскостей α и β?

А) Пересекаются В) Скрещиваются

С) Параллельны Д) Совпадают

Часть 2. Задание с развёрнутым ответом (2 балла).

Через концы отрезка MN и его середину К проведены параллельные прямые, пересекающие плоскость α в точках M _1, , N ₁ и К₁ . Найдите длину отрезка NN ₁ , если отрезок MN не пересекает α и ММ₁ = 10 см, KK ₁= 7см.

Даны две параллельные плоскости. Через точки А и В одной из плоскостей проведены две параллельные прямые до пересечения в точках А₁ и В₁. Найдите длину отрезка А₁ В₁ если АВ = 6 см.

Из точки М проведены к плоскости α до пересечения в точках N и К два отрезка. Точки D и Е – середины отрезков MN и МК. Найдите длину отрезка N К, если D Е = 10 см.

Через вершину острого угла прямоугольного треугольника АВС с прямым углом С проведена прямая А D , перпендикулярная плоскости треугольника. Чему равно расстояние от точки D до вершины С, если АС = 6 см; А D = 8 см.

Наклонная равна 2 см. Чему равна проекция этой наклонной на плоскость, если наклонная составляет с плоскостью угол равный 60 º ?

Отрезки двух наклонных, проведённые из одной точки до пересечения с плоскостью, равны 4 и 5 см, проекция одного из отрезков равна 4 см. Найдите проекцию другого отрезка.

Чему равен угол между плоскостью А₁В₁С₁ D ₁ и плоскостью проходящей через прямые C ₁ D ₁ и AB

Часть 3. Задание с развёрнутым ответом (3 балла).

Из точки А к плоскости α проведены два отрезка АС и АВ . Точка D принадлежит АВ, точка Е принадлежит АС. D Е параллельна α и равна 5 см. Найти длину отрезка ВС, если .

Из точки О пересечения диагоналей квадрата АВС D к е го плоскости восстановлен перпендикуляр ОМ так, что . Найдите косинус угла АВМ.

Из точки А построены три взаимоперпендикулярных отрезка АВ, АС и AD . Найдите длину отрезка С D если АС = c , ВС = в, В D = a

В кубе со стороной а найдите расстояние между прямыми AC ₁ и BB ₁.

Ответы для контрольной работы по стереометрии.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 964 человека из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 340 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 689 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Налетова Ирина АлександровнаНаписать 84964 17.03.2014

Номер материала: 35101031721

15.03.2014 1373

15.03.2014 960

14.03.2014 8916

14.03.2014 1282

14.03.2014 724

14.03.2014 3615

14.03.2014 2508

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

Число участников РДШ за 2021 год выросло в три раза

Время чтения: 2 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Параллельность прямой к плоскостиСкачать

Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости

Статья рассматривает понятия параллельность прямой и плоскости. Будут рассмотрены основные определения и приведены примеры. Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Параллельные прямые и плоскость – основные сведения

Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.

Параллельность обозначается « ∥ ». Если в задании по условию прямая a и плоскость α параллельны, тогда обозначение имеет вид a ∥ α . Рассмотрим рисунок, приведенный ниже.

Считается, что прямая a , параллельная плоскости α и плоскость α , параллельная прямой a , равнозначные, то есть прямая и плоскость параллельны друг другу в любом случае.

Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Параллельность прямой и плоскости – признак и условия параллельности

Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.

Если заданная прямая a , не лежащая в плоскости α , параллельна прямой b , которая принадлежит плоскости α , тогда прямая a параллельна плоскости α .

Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.

Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.

Подробное доказательство рассмотрено в учебнике 10 — 11 класса по геометрии. Необходимым и достаточным условием параллельности прямой с плоскостью возможно при наличии определения направляющего вектора прямой и нормального вектора плоскости.

Для параллельности прямой a , не принадлежащей плоскости α , и данной плоскости необходимым и достаточным условием является перпендикулярность направляющего вектора прямой с нормальным вектором заданной плоскости.

Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.

Допустим, прямая а в систему координат О х у задается каноническими уравнениями прямой в пространстве , которые имеют вид x — x 1 a x = y — y 1 a y = z — z 1 a z или параметрическими уравнениями прямой в пространстве x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , плоскостью α с общими уравнениями плоскости A x + B y + C z + D = 0 .

Отсюда a → = ( a x , a y , a z ) является направляющим вектором с координатами прямой а, n → = ( A , B , C ) — нормальным вектором заданной плоскости альфа.

Чтобы доказать перпендикулярность n → = ( A , B , C ) и a → = ( a x , a y , a z ) , нужно использовать понятие скалярного произведения. То есть при произведении a → , n → = a x · A + a y · B + a z · C результат должен быть равен нулю из условия перпендикулярности векторов.

Значит, что необходимым и достаточным условием параллельности прямой и плоскости запишется так a → , n → = a x · A + a y · B + a z · C . Отсюда a → = ( a x , a y , a z ) является направляющим вектором прямой a с координатами, а n → = ( A , B , C ) — нормальным вектором плоскости α .

Определить, параллельны ли прямая x = 1 + 2 · λ y = — 2 + 3 · λ z = 2 — 4 · λ с плоскостью x + 6 y + 5 z + 4 = 0 .

Получаем, что предоставленная прямая не принадлежит плоскости, так как координаты прямой M ( 1 , — 2 , 2 ) не подходят. При подстановке получаем, что 1 + 6 · ( — 2 ) + 5 · 2 + 4 = 0 ⇔ 3 = 0 .

Необходимо проверить на выполнимость необходимое и достаточное условие параллельности прямой и плоскости. Получим, что координаты направляющего вектора прямой x = 1 + 2 · λ y = — 2 + 3 · λ z = 2 — 4 · λ имеют значения a → = ( 2 , 3 , — 4 ) .

Нормальным вектором для плоскости x + 6 y + 5 z + 4 = 0 считается n → = ( 1 , 6 , 5 ) . Перейдем к вычислению скалярного произведения векторов a → и n → . Получим, что a → , n → = 2 · 1 + 3 · 6 + ( — 4 ) · 5 = 0 .

Значит, перпендикулярность векторов a → и n → очевидна. Отсюда следует, что прямая с плоскостью являются параллельными.

Ответ: прямая с плоскостью параллельны.

Определить параллельность прямой А В в координатной плоскости О у z , когда даны координаты A ( 2 , 3 , 0 ) , B ( 4 , — 1 , — 7 ) .

По условию видно, что точка A ( 2 , 3 , 0 ) не лежит на оси О х , так как значение x не равно 0 .

Для плоскости O x z вектор с координатами i → = ( 1 , 0 , 0 ) считается нормальным вектором данной плоскости. Обозначим направляющий вектор прямой A B как A B → . Теперь при помощи координат начала и конца рассчитаем координаты вектора A B . Получим, что A B → = ( 2 , — 4 , — 7 ) . Необходимо выполнить проверку на выполнимость необходимого и достаточного условия векторов A B → = ( 2 , — 4 , — 7 ) и i → = ( 1 , 0 , 0 ) , чтобы определить их перпендикулярность.

Запишем A B → , i → = 2 · 1 + ( — 4 ) · 0 + ( — 7 ) · 0 = 2 ≠ 0 .

Отсюда следует, что прямая А В с координатной плоскостью О y z не являются параллельными.

Ответ: не параллельны.

Не всегда заданное условие способствует легкому определению доказательства параллельности прямой и плоскости. Появляется необходимость в проверке принадлежности прямой a плоскости α . Существует еще одно достаточное условие, при помощи которого доказывается параллельность.

При заданной прямой a с помощью уравнения двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 , плоскостью α — общим уравнением плоскости A x + B y + C z + D = 0 .

Необходимым и достаточным условием для параллельности прямой a и плоскости α яляется отсутствие решений системы линейных уравнений, имеющей вид A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 .

Из определения следует, что прямая a с плоскостью α не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат О х у z не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 , а также уравнению плоскости A x + B y + C z + D = 0 .

Следовательно, система уравнений, имеющая вид A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 , называется несовместной.

Верно обратное: при отсутствии решений системы A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не существует точек в О х у z , удовлетворяющих всем заданным уравнениям одновременно. Получаем, что нет такой точки с координатами, которая могла бы сразу быть решениями всех уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 и уравнения A x + B y + C z + D = 0 . Значит, имеем параллельность прямой и плоскости, так как отсутствуют их точки пересечения.

Система уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.

Доказать , что прямая x — 1 = y + 2 — 1 = z 3 параллельна плоскости 6 x — 5 y + 1 3 z — 2 3 = 0 .

Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:

x — 1 = y + 2 — 1 = z 3 ⇔ — 1 · x = — 1 · ( y + 2 ) 3 · x = — 1 · z 3 · ( y + 2 ) = — 1 · z ⇔ x — y — 2 = 0 3 x + z = 0

Чтобы доказать параллельность заданной прямой x — y — 2 = 0 3 x + z = 0 с плоскостью 6 x — 5 y + 1 3 z — 2 3 = 0 , необходимо уравнения преобразовать в систему уравнений x — y — 2 = 0 3 x + z = 0 6 x — 5 y + 1 3 z — 2 3 = 0 .

Видим, что она не решаема, значит прибегнем к методу Гаусса.

Расписав уравнения, получаем, что 1 — 1 0 2 3 0 1 0 6 — 5 1 3 2 3

1 — 1 0 2 0 3 1 — 6 0 1 1 3 — 11 1 3

1 — 1 0 2 0 3 1 — 6 0 0 0 — 9 1 3 .

Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.

Делаем вывод, что прямая x — 1 = y + 2 — 1 = z 3 и плоскость 6 x — 5 y + 1 3 z — 2 3 = 0 параллельны, так как было выполнено необходимое и достаточное условие для параллельности плоскости с заданной прямой.

Ответ: прямая и плоскость параллельны.

🎥 Видео

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельность прямых, плоскостей, прямой и плоскости | Математика ЕГЭ для 10 класса | УмскулСкачать

Прямая параллельная плоскостиСкачать

Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

№110. Докажите, что в параллелепипеде ABCDA1B1C1D1 плоскость A1DB параллельна плоскости D1CB1.Скачать

№92. Плоскость α и прямая a параллельны прямой b. Докажите, что прямая a либо параллельна плоскостиСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ и ПЛОСКОСТИ стереометрия 10 классСкачать

6. Параллельность прямой и плоскостиСкачать

10 класс, 17 урок, Признак перпендикулярности прямой и плоскостиСкачать

№124. Прямая PQ параллельна плоскости α. Через точки Р и Q проведены прямые, перпендикулярныеСкачать

ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ и ПЛОСКОСТИ 10 11 класс стереометрияСкачать