Доказательство теоремы о медианах треугольника через векторы

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

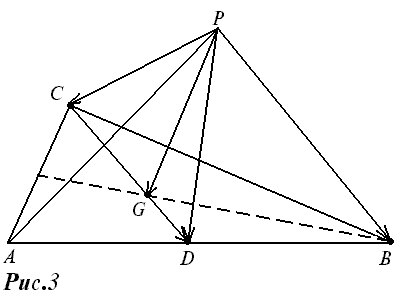
Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

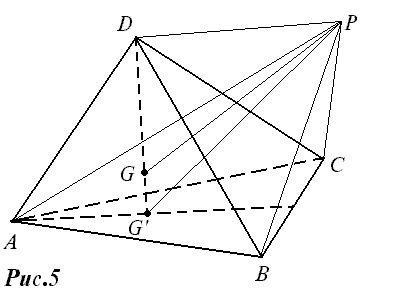
Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Видео:Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Доказательство теоремы о медианах треугольника через векторы

Две фигуры $$ F$$ и $$ ^<text>$$ называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между двумя точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры $$ F$$ и $$ ^<text>$$ подобны, то пишется $$ Fsim ^<text>$$Напомним, что в записи подобия треугольников $$ ∆ABC

Два треугольника подобны:

• 1) если два угла одного соответственно равны двум углам другого;
• 2) если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;
• 3) если три стороны одного треугольника пропорциональны трём сторонам другого.

Из признаков подобия следует утверждения, которые удобно использовать в решении задач:

1°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие в различных точках, отсекает треугольник, подобный данному.

Рис. 5

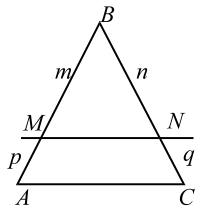
2°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие стороны, отсекает на них отрезки, пропорциональные данным сторонам, т. е. если $$ MNleft|right|AC$$ (рис. 5), то

3°. Если прямая пересекает две стороны треугольника и отсекает на них пропорциональные отрезки, то она параллельна третьей стороне, т. е. если (см. рис. 5)

то $$ MN$$ параллельна $$ AC$$ (доказательство было дано в задании для 9 класса).

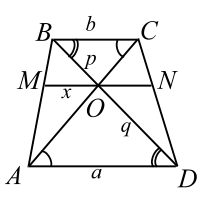
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках $$ M$$ и $$ N$$. Найти длину отрезка `MN`, если основания трапеции равны $$ a$$ и $$ b$$.

Пусть $$ O$$ точка пересечения диагоналей трапеции (рис. 6). Обозначим:

$$ AD=a, BC=b, MO=x, BO=p, OD=q.$$

$$1.;left.beginBCparallel AD\bigtriangleup BOCsimbigtriangleup DOA;(mathrm;mathrm;mathrm)endright|Rightarrowdfrac ba=dfrac pq$$ (1)

$$2.;left.beginMOparallel AD\bigtriangleup MBOsimbigtriangleup ABDendright|Rightarrowdfrac xa=dfrac p

$$. (2)

Результат этой задачи, как утверждение, верное для любой трапеции, следует запомнить.

Рис. 6

Из определения подобия фигур следует, что в подобных фигурах все соответствующие линейные элементы пропорциональны. Так, отношение периметров подобных треугольников равно отношению длин соответствующих сторон. Или, например, в подобных треугольниках отношение радиусов вписанных окружностей (также и описанных окружностей) равно отношению длин соответствующих сторон. Это замечание поможет нам решить следующую задачу.

Рис. 7

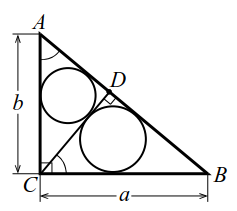
В прямоугольном треугольнике $$ ABC$$ из вершины $$ C$$ прямого угла проведена высота $$ CD$$ (рис. 7). Радиусы окружностей, вписанных в треугольники $$ ACD$$ и $$ BCD$$ равны соответственно $$ _$$ и $$ _$$. Найти радиус окружности, вписанной в треугольник $$ ABC$$.

Напомним, что площади подобных фигур относятся как квадраты соответствующих линейных элементов. Для треугольников это утверждение можно сформулировать так: площади подобных треугольников относятся как квадраты соответствующих сторон. Рассмотрим характерную задачу на эту тему.

Рис. 8

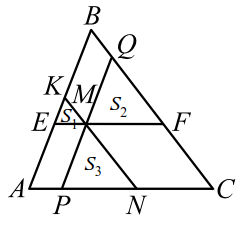
Через точку $$ M$$, лежащую внутри треугольника $$ ABC$$, проведены три прямые, параллельные его сторонам. При этом образовались три треугольника (рис. 8), площади которых равны $$ _$$, $$ _$$ и $$ _$$. Найти площадь треугольника $$ ABC$$.

Легко видеть, что треугольники $$ EKM$$, $$ MQF$$ и $$ PMN$$ подобны треугольнику $$ ABC$$.

Пусть $$ S$$ -площадь треугольника $$ ABC$$, тогда

А так как $$ EM=AP, MF=NC$$, то $$ EM+PN+MF=AP+PN+NC=AC$$.

Свойства медиан, высот, биссектрис треугольника

В наших заданиях 9-го и 10-го классов здесь повторяемые теоремы и утверждения были доказаны. Для некоторых из них мы напоминаем пути доказательств, доказывая их моменты и давая поясняющие рисунки.

Рис. 9

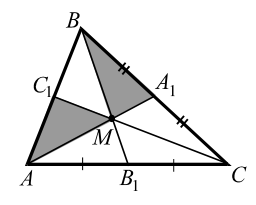
Теорема 1. Три медианы треугольника пересекаются в одной точке и точкой пересечения каждая медиана делится в отношении `2 : 1`, считая от вершины.

Теорема 2. Три медианы, пересекаясь, разбивают треугольник на `6` треугольников с общей вершиной, площади которых равны между собой.

(На рис. 9 площадь каждого из `6` треугольников с вершиной `M` и основанием, равным половине стороны, равна $$ <displaystyle frac>_$$. Точка пересечения медиан называется центром тяжести треугольника.

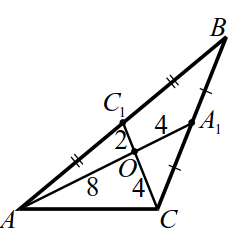
Теорема 3. Пусть $$ BD$$ — медиана треугольника

Рис. 10

Расставим на рисунке 10 длины отрезков медиан. По условию, одна из сторон треугольника равна `12`, сторона $$ AC$$ не может равняться `12`, иначе $$ AC=AO+OC$$ — нарушено неравенство треугольника. Также не может равняться `12` сторона $$ AB$$, так в этом случае $$ A_=6$$ и треугольник $$ AO_$$ со сторонами `8`, `2`, `6` не существует. Значит, $$ BC=12$$ и $$ A_=6$$.

2. Площадь треугольника находим по формуле Герона:

По теореме 2 площадь треугольника $$ ABC$$ в `6` раз больше, находим $$ _=18sqrt$$.

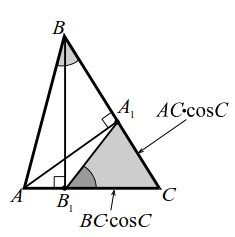
Теорема 4. Три высоты треугольника или три прямые, на которых лежат высоты, пересекаются в одной точке. (Эта точка называется ортоцентром треугольника). В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.

Были доказаны также две леммы о высотах

1-ая лемма.

Рис. 11a	Рис. 11б

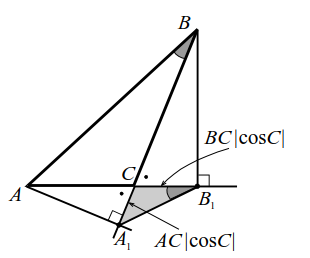
2-ая лемма.

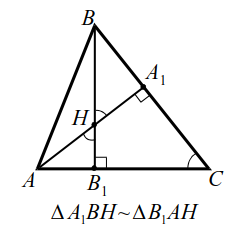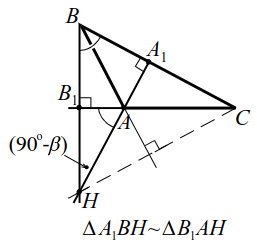Рис. 12a	Рис. 12б

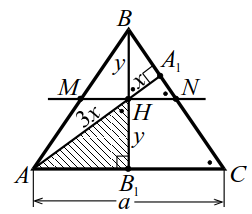Рис. 13

1. Точка $$ H$$ — середина высоты (рис. 13). Если отрезок $$ MH$$ проходит через точку $$ H$$ и параллелен основаниям, то `MN` — средняя линия; `MN=a/2`.

3. $$ angle _BC=90°-angle C$$, поэтому `ul(/_BHA_1=/_AHB_1=/_C)`, а по второй лемме о высотах $$ AH·H_=BH·H_$$ т. е. $$ 3^=^, y=xsqrt$$.

Теорема 5. Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если $$ AD$$ — биссектриса треугольника $$ ABC$$ (рис. 14), то

Доказательство легко выполните сами, применяя теорему синусов к треугольникам $$ ADB$$ и $$ ADC$$.

Теорема 6. Пусть $$ AD$$ — биссектриса треугольника $$ ABC$$ (рис. 14), тогда $$ AD=sqrt$$ (в обозначениях рисунка 14а)

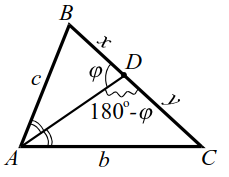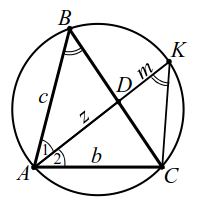Рис. 14	Рис. 14а

Эту теорему докажем. Опишем около треугольника $$ ABC$$ окружность, точку пересечения прямой $$ AD$$ и окружности обозначим $$ K$$ (рис. 14а).

По свойству пересекающихся хорд: $$ AD·DK=BD·CD$$, т. е. $$ z·m=x·y$$, тогда $$ ^=bc-xy$$, $$ z=sqrt$$.

В треугольнике $$ ABC$$ со сторонами $$ AB=5$$, $$ AC=3$$ биссектриса $$ AD=<displaystyle frac>$$. Найти сторону $$ BC$$ и радиус вписанной окружности.

Видео:Как доказать теорему о медианах треугольника с использованием методов векторной алгебры?Скачать

Прямая Эйлера

Деление отрезка в данном отношении.

Теорема о пересечении медиан треугольника в одной точке.

Теорема о высотах произвольного треугольника.

Прямая Эйлера тетраэдра.

Использованные источники информации.

Свойства треугольника были хорошо изучены еще древними греками.

В знаменитых “Началах” Евклида доказывается, что центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к его сторонам.

Архимед, определяя положение центра тяжести однородной треугольной пластинки, установил, что он лежит на каждой из трех медиан. Точку пересечения медиан треугольника называют центром тяжести или центроидом треугольника.

Позднее было доказано, что три высоты треугольника также пересекаются в одной точке, которая называется его ортоцентром.

Закономерность в расположении этих трех замечательных точек треугольника – центра O описанной окружности, центроида G , ортоцентра H – впервые обнаружил знаменитый математик Леонард Эйлер (1707-1783).

Рассмотрим сначала один частный случай: прямоугольный треугольник ABC (рис.1). Середина O гипотенузы AB является центром описанной около него окружности. Центроид G делит медиану CO в отношении 1:2, считая от вершины C. Катеты AC и BC являются высотами треугольника, поэтому вершина C прямого угла совпадает с ортоцентром H треугольника. Таким образом, точки O,G,H лежат на одной прямой, причем OH=3OG. Пользуясь методом координат, Эйлер доказал, что такая же связь существует между тремя указанными точками любого треугольника. Мы докажем этот факт с помощью векторов.

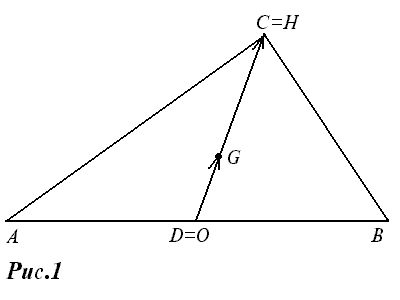
Деление отрезка в данном отношении.

Пусть A,B,O – данные точки плоскости, и известно, что

точка G делит отрезок AB в отношении k: ——- = k (рис.2).

Выразим вектор OG через векторы OA и OB. Для этого подставим в равенство AG=k * GB выражения всех векторов через OG, OA и OB: OG-OA=k(OB-OG). Решая это уравнение относительно OG , получим:

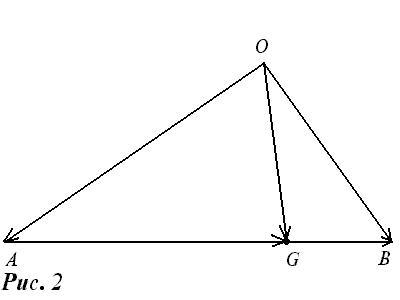
Например, если G – середина отрезка AB , то k=1 и OG= — (OA+OB).

Теорема о пересечении медиан треугольника в одной точке.

Здесь мы попутно получим одно векторное равенство, которое понадобится нам в дальнейшем.

Теорема 1. Медианы треугольника АВС пересекаются в одной точке G и делятся ею в отношении 2:1, считая от вершины, причем

где P – любая точка плоскости или пространства.

Доказательство. Возьмем на медиане CD треугольника ABC точку G, определяемую соотношением |CG|:|GD|=2:1 (рис. 3).

Согласно формуле (1),

PG = — (PA + PB + PC).

Вычисляя вектор PG’ с концом в точке G’, делящей любую из двух других медиан треугольника в отношении 2:1 (считая от вершины), мы получим то же самое выражение:

Поэтому PG’=PG, и точка G’ совпадает с точкой G. Следовательно, все три медианы треугольника пересекаются в одной точке G, определяемой соотношением (2).

Теорема о высотах произвольного треугольника.

Теорема 2. Высоты треугольника АВС пересекаются в одной точке Н, причем

OH= OA + OB + OC, (3)

где О – центр окружности описанной около треугольника.

Доказательство. Пусть АВС – треугольник, отличный от прямоугольного (рис.4).

Найдем сумму векторов OA и OB. Для этого построим точку M, симметричную О относительно стороны AB, тогда OM = OA + OB. Затем построим точку Н, для которой

OH = OM + OC = OA + OB +OC,

и докажем, что точка H и есть ортоцентр треугольника АВС.

Действительно, по построению прямые CH и OM параллельны, OM – серединный перпендикуляр к отрезку АВ, следовательно, прямая СН также перпендикулярна к прямой AB, и точка H лежит на высоте треугольника ABC, проведенной из вершины C.

Если повторить построение, начиная с векторов OA и OC, то получится та же точка H, но те же рассуждения показывают, что теперь точка H лежит на высоте треугольника, проведенной из вершины B. Аналогично получим, что точка H лежит на высоте, проведенной из вершины A. Следовательно, высоты треугольника ABC пересекаются в точке H, определяемой соотношением (3).

Легко проверить, что теорема 2 справедлива и для прямоугольного треугольника.

Из доказанных теорем 1 и 2 вытекает интересующее нас свойство замечательных точек треугольника.

Теорема 3. Центр О описанной окружности, центроид G и ортоцентр H любого треугольника лежат на одной прямой, причем точка G лежит между точками О и Н и OG:GH = 1:2.

Доказательство. По теореме 1

3OG = OA + OB + OC.

Сравнивая это равенство с равенством (3), получим

Следовательно, векторы OH и OG, имеющие общее начало O, расположены на одной прямой и | OG| : |GH| = 1 : 2.

Прямая, на которой лежат точки O, G и H, называется прямой Эйлера.

В стереометрии простейший многогранник – тетраэдр играет ту же роль, что и треугольник в планиметрии. Свойства треугольника и тетраэдра во многом схожи. Попробуем распространить свойство замечательных точек треугольника на тетраэдр.

Сфера, описанная около тетраэдра.

Известно, что около всякого тетраэдра можно описать сферу, её центр O лежит на перпендикулярах к граням тетраэдра, восстановленных в центрах окружностей, описанных около граней.

Отрезок, соединяющий вершину тетраэдра с центроидом противоположной грани, называется медианой тетраэдра. Свойства медиан тетраэдра аналогичны свойствам медиан треугольника.

Теорема 4. Четыре медианы тетраэдра ABCD пересекаются в одной точке G, которая делит каждую из них в отношении 3:1, считая от вершины тетраэдра, причем

4PG = PA + PB +PC +PD, (4)

где P – любая точка пространства.

Доказательство. Возьмем на медиане DG’ тетраэдра ABCD точку G, определяемую соотношением DG : GG’ = 3 : 1 (рис 5). Согласно формуле (1),

Учитывая, что центроид G’ треугольника ABC удовлетворяет соотношению 3PG = PA + PB + PC, получим

PG = — (PA + PB + PC + PD).

Вычисляя вектор PG’’ с концом в точке G’’ , делящей любую из трех других медиан тетраэдра в отношении 3 : 1 (считая от вершины), получим то же самое выражение. А это означает, что все четыре медианы тетраэдра пересекаются в одной точке G, удовлетворяющей соотношению (4). Точка G, называется

центром тяжести (или центроидом) тетраэдра.

Высоты треугольника всегда пересекаются в одной точке. По аналогии можно предположить, что высоты любого тетраэдра также пересекаются в одной точке. Однако это не так.

Для примера рассмотрим тетраэдр ABCD с прямым двугранным углом при ребре AB, в котором AC = BC, но AD = BD (рис. 6). Высоты CE и DF тетраэдра лежат соответственно в гранях ABC и ABD, но точка E – середина AB, а F – нет. Если бы длины ребер DA и DB были равны, то основания E и F совпадали бы, но две другие высоты тетраэдра не могут проходить через точку E.

Таким образом, даже две высоты тетраэдра могут не иметь общей точки.

Тем не менее существуют и тетраэдры, все четыре высоты которых пересекаются в одной точке. Таким будет, например, тетраэдр ABCD с прямыми плоскими углами при вершине D. Ребра DA, DB и DC являются его высотами, а вершина D – ортоцентром (точкой пересечения всех четырех высот).

Попробуем найти все тетраэдры, у которых высоты пересекаются в одной точке.

Пусть высоты тетраэдра ABCD, проведенные из вершин C и D , пересекаются в точке H

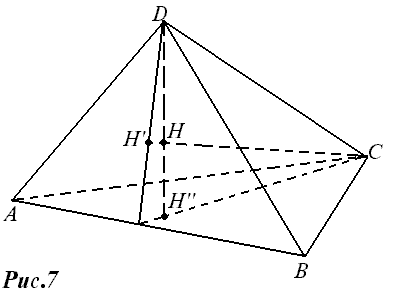
(рис. 7). Тогда CH’__AB и DH’’__AB, т.е. прямая AB перпендикулярна к двум пересекающимся прямым лежащим в плоскости CDH, следовательно, AB__BC. Аналогично доказывается, что если две другие высоты тетраэдра ABCD проходят через ту же точку H, то AC__BD и AD__BC. Итак, если все высоты тетраэдра пересекаются в одной точке, то противоположные ребра тетраэдра взаимно перпендикулярны. Такой тетраэдр называется ортоцентрическим.

Теорема 5. Четыре высоты ортоцентрического тетраэдра ABCD пересекается в одной точке H, причем если O – центр сферы, описанной около тетраэдра, то

OH = —(OA + OB + OC + OD). (5)

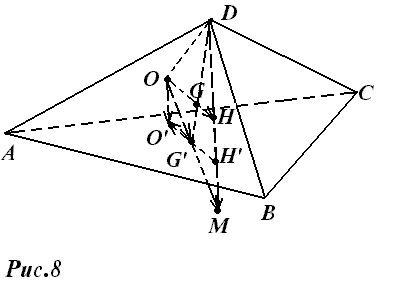
Доказательство. Пусть ABCD – ортоцентрический тетраэдр, DG’ – его медиана, DH’ – его высота (рис.8). Тогда G’ центроид, а H’- ортоцентр треугольника ABC, причем точки O’ (центр окружности, описанной около треугольника ABC ), G’ и H’ лежат на одной прямой. Заметим, что центр O сферы, описанной около тетраэдра ABCD, лежит на перпендикуляре к плоскости треугольника ABC, восстановленном в точке O’.

Будем доказывать теорему тем же способом, что и теорему 2 для треугольника: строить разными способами точку H, удовлетворяющую соотношению (5).

Вначале сложим векторы OA, OB и OC:

OG’ = — (OA + OB + OC),

или G’M = 2OG’ . Точки O’,G’,H’, лежат на прямой Эйлера треугольника ABC, причем H’G’ = 2G’O’. Следовательно,

Отсюда вытекает, что прямые H’M и OO’ параллельны, а так как прямая OO’ перпендикулярна к плоскости ABC, то и прямая H’M перпендикулярна к этой плоскости. Следовательно, точка M’ лежит на прямой DH’ (если точки O и O’ совпадают, то точки M и H’ тоже совпадают).

Из левого равенства следует, что точка H является серединой отрезка DM, т.е. точка H лежит на DH’ тетраэдра.

Аналогично строится точка N: ON=OA+OB+OD и та же точка H: OH= —(ON+OC) и доказывается, что точка H лежит на высоте тетраэдра, проведенной из вершины C, и т.д.

Следовательно, высоты ортоцентрического тетраэдра пересекаются в одной точке H, определяемой соотношением (5).

Прямая Эйлера тетраэдра.

Теорема 6. Центр О описанной сферы, центроид G и ортоцентр Н ортоцентрического тетраэдра ABCD лежат на одной прямой, причем точки О и Н симметричны относительно точки G.

Доказательство. По формулам (4) и (5)

OH= — (OA + OB + OC +OD),

OG= — (OA + OB + OC + OD),

откуда OH=2OG. Полученное равенство означает, что точки O, G, H лежат на одной прямой, причем точки О и Н симметричны относительно точки G.

Прямую, на которой лежат точки O, G, H, можно назвать прямой Эйлера ортоцентрического тетраэдра.

В данном реферате собран материал необходимый для выявления прямой Эйлера и прямой Эйлера тетраэдра .

Использованные источники информации:

“Прямая Эйлера” (Э. Готман).

Международная информационная сеть Internet (URL: ).

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

🎬 Видео

8. Медиана треугольника и её свойства.Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Теорема о трёх медианахСкачать

№786. Отрезки AA1, ВВ1 и СС1 — медианы треугольника ABC. Выразите векторы AA1, BB1, СС1Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

22 Медианы треугольника пересекаются в одной точкеСкачать

Точка пересечения медиан в треугольникеСкачать

Длина медианы треугольникаСкачать

Задача о векторах, построенных на медиане, биссектрисе и высоте треугольникаСкачать

Уравнения стороны треугольника и медианыСкачать

№110. Докажите, что если медиана треугольника совпадает с его высотой, то треугольникСкачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать

№787. Точка О — середина медианы EG треугольника DEF. Выразите вектор DO черезСкачать

Свойство биссектрисы треугольника с доказательствомСкачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

🔥 Свойства МЕДИАНЫ #shortsСкачать