Доказательство линейных свойств векторов (3 видео)

Операции над векторами и их свойства: сложение и умножение

Прежде чем приступить к тематике статьи, напомним основные понятия.

Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.

Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.

Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.

Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.

Содержание

Сложение двух векторов
Сложение нескольких векторов
Умножение вектора на число
Свойства операций над векторами
Линейные операции над векторами
Сложение векторов
Вычитание векторов
Умножение вектора на число
Свойства линейных операций над векторами
Линейные комбинации векторов
Линейная зависимость векторов
Свойства линейно независимых векторов
🎬 Видео

Видео:Лекция 18. Скалярное произведение векторов и его свойства.Скачать

Сложение двух векторов

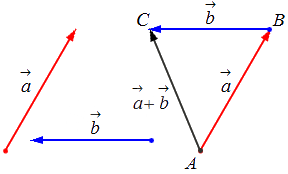
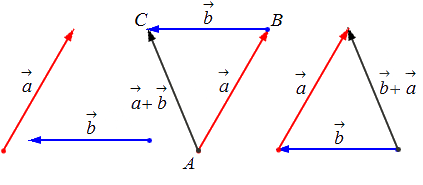
Исходные данные: векторы a → и b → . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор A B → , равный вектору а → ; из полученной точки undefined – вектор В С → , равный вектору b → . Соединив точки undefined и C , получаем отрезок (вектор) А С → , который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.

Геометрически сложение векторов выглядит так:

— для неколлинеарных векторов:

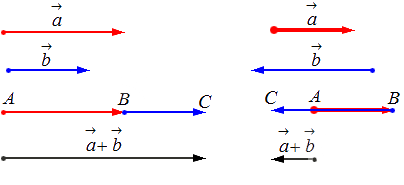
— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:

Видео:Лекция 19. Векторное произведение векторов и его свойства.Скачать

Сложение нескольких векторов

Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.

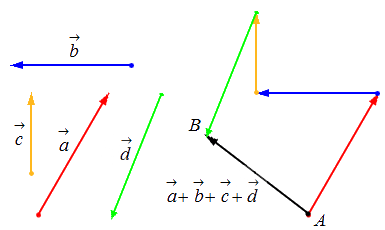
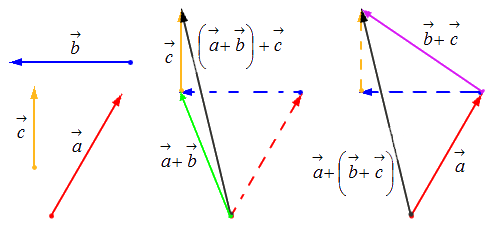
Исходные данные: векторы a → , b → , c → , d → . Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a → ; затем от конца полученного вектора откладывается вектор, равный вектору b → ; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B , а полученный отрезок (вектор) A B → – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .

Геометрически оно выглядит следующим образом:

Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a → и b → есть сумма векторов a → и — b → .

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Умножение вектора на число

Чтобы произвести действие умножения вектора на некое число k , необходимо учитывать следующие правила:
— если k > 1 , то это число приведет к растяжению вектора в k раз;
— если 0 k 1 , то это число приведет к сжатию вектора в 1 k раз;
— если k 0 , то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
— если k = 1 , то вектор остается прежним;
— если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.

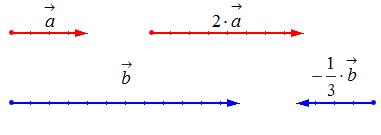
Исходные данные:
1) вектор a → и число k = 2 ;
2) вектор b → и число k = — 1 3 .

Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:

Видео:Линейная зависимость векторовСкачать

Свойства операций над векторами

Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.

Исходные данные: векторы a → , b → , c → и произвольные действительные числа λ и μ .

Свойство коммутативности: a ⇀ + b → = b → + a → .
Свойство ассоциативности: ( a → + b → ) + c → = a → + ( b → + c → ) .
Свойство использования нейтрального элемента по сложению (нулевой вектор 0 → ⃗). Это очевидное свойство: a → + 0 → = a →
Свойство использования нейтрального элемента по умножению (число, равное единице): 1 · a → = a → . Это очевидное свойство, не предполагающее никаких геометрических преобразований.
Любой ненулевой вектор a → имеет противоположный вектор — a → и верным является равенство: a → + ( — a → ) = 0 → . Указанное свойство — очевидное.
Сочетательное свойство операции умножения: ( λ · µ ) · a → = λ · ( µ · a → ) . Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
Первое распределительное свойство (очевидно): ( λ + µ ) · a → = λ · a → + µ · a → .
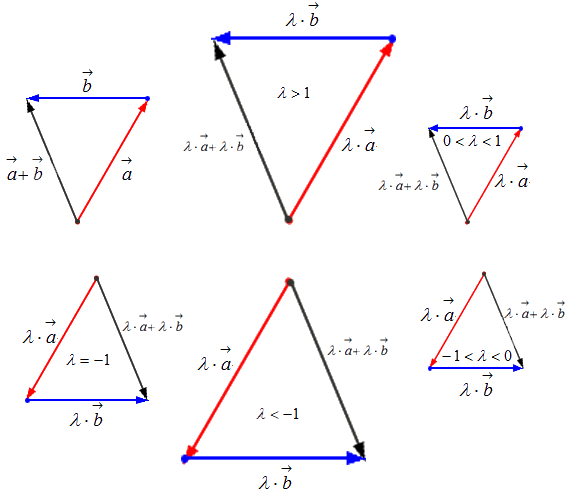
Второе распределительное свойство: λ · ( a → + b → ) = λ · a → + λ · b → .
Геометрически это свойство определяется подобием треугольников:

Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.

Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.

Задача: упростить выражение a → — 2 · ( b → + 3 · a → )
Решение
— используя второе распределительное свойство, получим: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · ( 3 · a → )
— задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a → — 2 · b → — 2 · ( 3 · a → ) = a → — 2 · b → — ( 2 · 3 ) · a → = a → — 2 · b → — 6 · a →
— используя свойство коммутативности, меняем местами слагаемые: a → — 2 · b → — 6 · a → = a → — 6 · a → — 2 · b →
— затем по первому распределительному свойству получаем: a → — 6 · a → — 2 · b → = ( 1 — 6 ) · a → — 2 · b → = — 5 · a → — 2 · b → Краткая запись решения будет выглядеть так: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · 3 · a → = 5 · a → — 2 · b →
Ответ: a → — 2 · ( b → + 3 · a → ) = — 5 · a → — 2 · b →

Видео:Линейная зависимость и линейная независимость векторов.Скачать

Линейные операции над векторами

Видео:Свободные вектора. Линейные операции и их свойства. Векторное пространство как линейное.Скачать

Сложение векторов

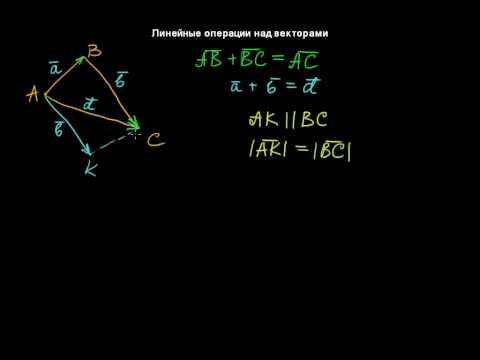
Пусть даны два вектора и . Приложим вектор к точке (концу вектора ) и получим вектор (рис.1.7,а; здесь и далее равные векторы отмечены одинаковыми засечками). Вектор называется суммой векторов и и обозначается . Это нахождение суммы называется правилом треугольника .

Сумму двух неколлинеарных векторов и можно найти по правилу параллелограмма . Для этого откладываем от любой точки векторы и , а затем строим параллелограмм (рис. 1.7,6). Диагональ параллелограмма определяет сумму:

Для нахождения суммы нескольких векторов можно построить ломаную из равных им векторов. Тогда замыкающий вектор, соединяющий начало первого вектора ломаной с концом последнего ее вектора, равен сумме всех векторов ломаной. На рис.1.7,в изображена сумма четырех векторов . Таким способом ( правило ломаной ) можно сложить любое конечное число векторов. Заметим, что сумма векторов не зависит от точек приложения слагаемых и от порядка суммирования. Например, «выстраивая цепочку» векторов для суммы в виде , получим вектор, равный вектору . Если ломаная получилась замкнутой, то сумма равна нулевому вектору.

Видео:§2 Линейная операция над векторамиСкачать

Вычитание векторов

Вектор называется противоположным вектору , если их сумма равна нулевому вектору: . Противоположный вектор имеет длину , коллинеарен и противоположно направлен вектору (рис.1.8,а,б). Нулевой вектор является противоположным самому себе.

Разностью векторов и называется сумма вектора с вектором , противоположным вектору :

Для нахождения разности векторов и приложим к произвольной точке векторы и , а также вектор , противоположный вектору (рис.1.9,а). Искомую разность находим по правилу параллелограмма:

Для нахождения разности проще использовать правило треугольника (рис. 1.9,6). Для этого прикладываем к произвольной точке векторы и . Вектор при этом равен искомой разности

Вычитание векторов — действие, обратное сложению — можно определить также следующим образом: разностью векторов и называется такой вектор , который в сумме с вектором дает вектор (рис.1.9,в), т.е. разность — это решение линейного векторного уравнения .

Пример 1.2. Для векторов, изображённых на рис. 1.6 (в конце), найти следующие суммы и разности:

Решение. Учитывая равенство , получаем по правилу треугольника .

Поскольку и , то .

По правилу параллелограмма . Так как и , находим

Видео:Скалярное произведение векторов. 9 класс.Скачать

Умножение вектора на число

Произведением ненулевого вектора на действительное число называется вектор , удовлетворяющий условиям:

1) длина вектора равна , т.е. ;

2) векторы и коллинеарные ;

3) векторы и одинаково направлены, если 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAQBAMAAACigOGCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAvydBYeqhkaCBEdFRcZpXsy0AAADDSURBVBjTY2DACXglMcWMwWSeA7q4aXkwiNITQBNnCmFwVQDSjI/AXA0FmAT7Awa+AiDN8hbMZZaAybAKMDBuANJcryF85kQDCIMPKPEAxJCDKmVqPMAAtZTxFYjhVwCzNRXsQDugxGMQNzQAZi3X7ANIEq5qb1AloHawPGZ+BjNqtgPMVUBD/BwYQhdALYeEARvQHwkMLM8ZGOY5QMShzmV+zGBnAJJjUAUFCrOgAcwq17shQHUgtSAhNQVEYLkoMAAA/y0j/mOlY6gAAAAASUVORK5CYII=» />, и противоположно направлены, если .

Произведение нулевого вектора на любое число считается (по определению) нулевым вектором: ; произведение любого вектора на число нуль также считается нулевым вектором: . Из определения произведения следует, что:

а) при умножении на единицу вектор не изменяется: ;

б) при умножении вектора на получается противоположный вектор: ;

в) деление вектора на отличное от нуля число сводится к его умножению на число , обратное .

г) при делении ненулевого вектора на его длину, т.е. при умножении на число получаем единичный вектор, одинаково направленный с вектором .

Действительно, длина вектора равна единице: .

Вектор коллинеарен и одинаково направлен с вектором , так как 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAGgAAAAwBAMAAAAP7yIIAAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADnRSTlMAgUH7J8EBn5MRZNNSscg1DbUAAAGiSURBVEjHY2CgLnAkXQuTrGkCyZqSlpChiS2NDE0MbHTUxDC4nTeYNbEoGktNwJ3IwrHKMQkKCjpgEedUAVPKF0hxgbBsCIjitiRBD5cJQzXIr1lWBJWugvsg+wKD8gGQlwmnF66NMF3OAgyTG0CMYAeCurJ2QNUoCzAkh4EYixeASCclEFDBoSsnHKJLGKbJeRsoLh0FQUAGd8wowDSZgUJ+twmIm4ZQMKMDAQTguq46IGmavcYCzVT3cgSAa2IpBWk6DHEey3Y2Y1DIE3JeqEIaNPQuMLA5X2AoPkAwIJIgAcGWDIynBQws1hMYnAvgkmnYkzbXdmiQM1oyNE9gYN3JwIaZkI6g0lwb4VFZvQIYbCzAuObURNckBE6UUJqBYSEiI7DI4MwwQgwLBQWlBWCakEAa7mQjxOCkKHh5ARZNeEARGzBAWhhI0xQEDt8EkjWxSM0k3abFZ4IXkKoJmK+bFUjVBExhxST7SXgB21aS/XTZgcWQZE3BCVxGXqRqKk6YbdZDqibnNTeswkjVxLlmguIEMpIRA8Ow0uSARqMCAGU+ZLrFh1ZQAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />;

д) при умножении единичного вектора на число получаем коллинеарный ему вектор, длина которого равна .

На рис.1.10 изображены векторы, получающиеся в результате умножения данного вектора на и , а также противоположный вектор .

Видео:Линейная алгебра. Векторы и операции над векторами.Скачать

Свойства линейных операций над векторами

Сложение векторов и умножение вектора на число называются линейными операциями над векторами . Для любых векторов , , и любых действительных чисел справедливы равенства:

Свойства 1, 2 выражают коммутативность и ассоциативность операции сложения векторов, свойство 5 — ассоциативность операции умножения на число, свойства 6,7 — законы дистрибутивности, свойство 8 называется унитарностью.

Свойства линейных операций устанавливают такие же правила действия с векторами, как с алгебраическими выражениями.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Линейные комбинации векторов

Применяя линейные операции, можно составлять суммы векторов, умноженных на числа.

Вектор называется линейной комбинацией векторов , если он может быть представлен в виде

где — некоторые числа. В этом случае говорят, что вектор разложен по векторам , а числа называют коэффициентами разложения.

Линейная комбинация с нулевыми коэффициентами называется тривиальной.

Отметим следующие свойства линейных комбинаций векторов:

1. Если векторы — коллинеарны, то любая их линейная комбинация им коллинеарна.

2. Если векторы — компланарны, то любая их линейная комбинация им компланарна.

Докажем, например, первое свойство. При умножении вектора на число получаем (по определению) вектор, колпинеарный данному. При сложении двух векторов, параллельных некоторой прямой, получаем (по определению) вектор, параллельный той же самой прямой. Поэтому линейная комбинация двух коллинеарных векторов и коллинеарна им. По индукции свойство распространяется на любое конечное число коллинеарных
векторов.

Видео:Линейная зависимость векторов на примерахСкачать

Линейная зависимость векторов

Содержание:

Вначале введем часто используемые в приложениях, понятия коллинеарности и компланарности векторов.

Определение 1.4.1. Два вектора, параллельные одной и той же прямой, называются коллинеарными. Три вектора, параллельные одной и той же плоскости, называются компланарными. Нулевой вектор считается коллинеарным любому другому вектору. Нулевой вектор считается компланарным любой паре векторов.

Определение 1.4.2. Выражение вида —некоторые числа, называется линейной комбинацией векторов

Если все числа равны нулю одновременно (что равносильно условию то такая линейная комбинация называется тривиальной.

Если хотя бы одно из чисел отлично от нуля (то есть то данная линейная комбинация называется нетривиальной.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Соглашение о суммировании

В тех случаях, когда явная запись суммы некоторого числа слагаемых нецелесообразна или невозможна, но известно, как зависит значение каждого из слагаемых от его номера, то допускается использование специальной формы записи операции суммирования:

(читается: «Сумма F(k) по «). где — индекс суммирования, мальное значение индекса суммирования, N — максимальное значение индекса суммирования и, наконец, F(k) — общий вид слагаемого.

Пример с решением 1.4.1.

По соглашению о суммировании будут справедливы следующие равенства Используя данную символику, линейную комбинацию можно записать в виде

Возможно вам будут полезны данные страницы:

Приведем теперь определение важного понятия линейной зависимости системы векторов.

Определение 1.4.3. Векторы называются линейно зависимыми, если существует их нетривиальная линейная комбинация такая, что Определение 1.4.4. Векторы называются линейно независимыми, если из условия следует тривиальность линейной комбинации то есть, что Иначе говоря, векторы линейно независимы, если для любого набора чисел не равных нулю одновременно, линейная комбинация не равна

Справедливы следующие утверждения:

Теорема 1.4.1. Один вектор линейно зависим тогда и только тогда, когда он нулевой.

Теорема 1.4.2. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Теорема 1.4.3. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Теоремы 1.4.1. и 1.4.2. предлагаются для самостоятельного доказательства. Здесь же мы рассмотрим подробно теорему 1.4.З., доказав предварительно следующее вспомогательное утверждение:

Лемма 1.4.1. Для линейной зависимости векторов , необходимо и достаточно, чтобы один из них был линейной комбинацией остальных. Доказательство:

Докажем необходимость. Пусть векторы линейно зависимы, тогда существуют числа одновременно не равные нулю, такие что Для определенности можно считать, что но тогда что и доказывает необходимость. Докажем достаточность. Пусть для определенности тогда причем То есть нетривиальная линейная комбинация векторов равна нулевому вектору.

Докажем теперь теорему 1.4.3.

Докажем необходимость. Пусть три вектора линейно зависимы, то есть существуют три, одно временно не равных нулю, числа , таких, что Тогда, по лемме 1.4.1. один из векторов есть линейная комбинация двух остальных и, значит, данные три вектора компланарны. Докажем достаточность в предположении, что векторы неколлинеарны. Пусть даны три компланарных вектора Перенесем эти векторы таким образом, чтобы их начала попали в одну точку.

Через конец вектора проведем прямые, параллельные векторам При этом получим пару векторов таких, что (Рис. 1.4.1.) Поскольку вектор коллинеарен вектору , а вектор коллинеарен вектору по теореме 1.4.2. получаем, что но, с другой стороны, имеем и векторы по лемме 1.4.1., линейно зависимы.

Случай коллинеарных рассмотрите самостоятельно.

Свойства линейно независимых векторов

1°. Один вектор линейно независим тогда и только тогда, когда он ненулевой.
2°. Два вектора линейно независимы тогда и только тогда, когда они неколлинеарны.
3°. Три вектора линейно независимы тогда и только тогда, когда они некомпланарны.

Теорема 1.4.4. Если среди векторов имеется подмножество линейно зависимых, то и все векторы линейно зависимы. Доказательство: Без ограничения общности можно считать, что линейно зависимы первые векторов (иначе, просто перенумеруем эти векторы), то есть существуют не равные нулю одновременно, числа такие, что Построим нетривиальную линейную комбинацию векторов взяв в качестве первых к коэффициентов числа и нули в качестве остальных. Тогда получим, что Теорема доказана.

Следствие 1.4.1. Если среди векторов имеется хотя бы один нулевой, то векторы линейно зависимы.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.