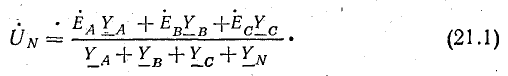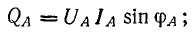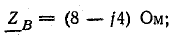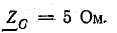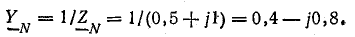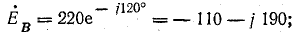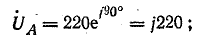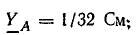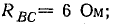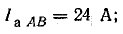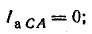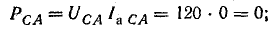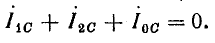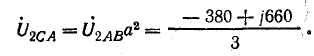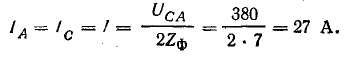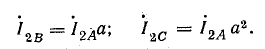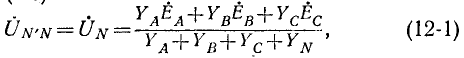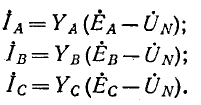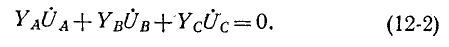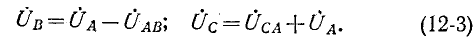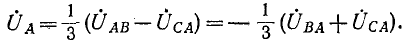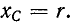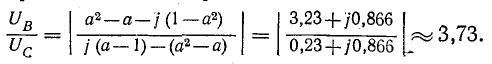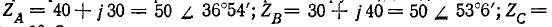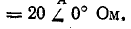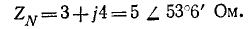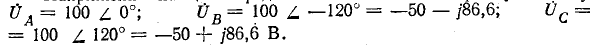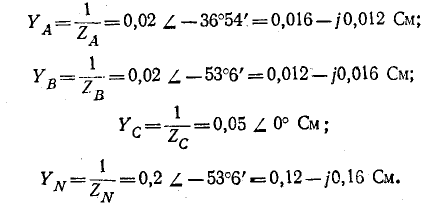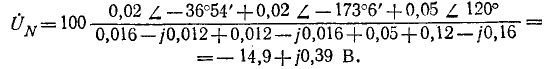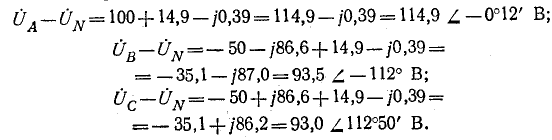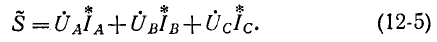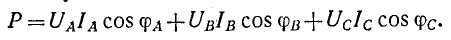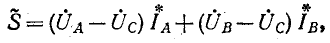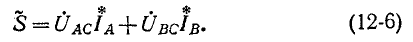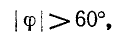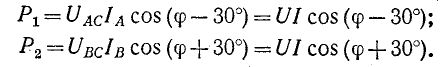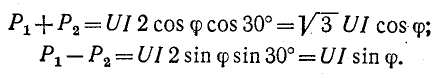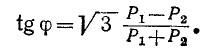Несимметричный режим трехфазных цепей

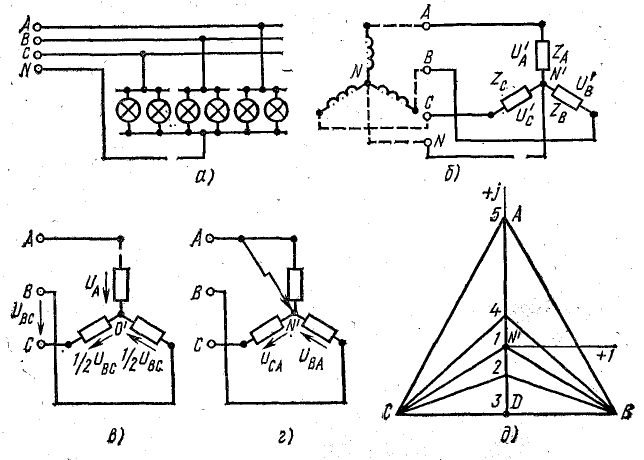
а) Назначение нулевого провода.
При несимметричной нагрузке звездой без нулевого провода (на рис. 11.19 ключ разомкнут) сопротивления всех фаз неодинаковы: Z А Z В Z С . Вследствие этого появляется напряжение смещения нейтрали U _N’N , определяемое по формуле двух узлов:

Это напряжение U _N, действующее между точками N и N’ (рис. 11.19), показано на рис. 11.20. При любом направлении вектора U _N напряжения на фазах нагрузки будут неодинаковы.

При включении и выключении приемников проводимости фаз Y А, Y B и Y C изменяются произвольным образом, это приводит к изменению напряжения смещения нейтрали U _N, ведущее, в свою очередь, к произвольному изменению напряжений на фазах нагрузки. Подавляющее большинство электросиловых приемников функционирует только при номинальном питающем напряжении. Поэтому соединение звездой без нулевого провода для несимметричной или изменяемой нагрузки практически не используется вследствие невозможности обеспечить номинальное питающее напряжение. При большом числе приемников, статистически в «среднем» обеспечивающих примерно одинаковую нагрузку фаз, несмотря на включение и выключение отдельных потребителей, смещение нейтрали невелико. Это позволяет использовать соединение звездой без нулевого провода для мощных линий электропередач на трансформаторные подстанции напряжением до 6,3 кВ. Соединение звездой без нулевого провода используется и в устройствах, предназначенных для контроля и анализа режимов трехфазных цепей.

б) Соединение звездой с нулевым проводом.
Для соединения звездой с нулевым проводом (на рис. 11.19 ключ замкнут) определим напряжение нейтрали также по формуле двух узлов:

В реальных системах электроснабжения проводимость нулевого провода Y _N много больше проводимостей фаз и практически можно считать, что сопротивление нулевого провода близко к нулю. Тогда при Y _N → ∞ знаменатель в выше написанной формуле стремится к бесконечности, U _N → 0 и при наличии нулевого провода с достаточно малым сопротивлением смещение потенциала нулевой точки N’ нагрузки отсутствует. На фазах нагрузки независимо от их сопротивлений поддерживаются напряжения, составляющие симметричную трехфазную систему.
Токи фаз нагрузки определяются по закону Ома:

На рис. 11.22 показана векторная диаграмма токов при несимметричной активной нагрузке. Из векторной диаграммы видно, что токи фаз при несимметричной нагрузке не равны по модулю, а в общем случае смещены по фазе на углы, не равные 120°, т. е. они не представляют симметричную трехфазную систему.
Ток нейтрального провода (см. рис. 11.14) можно определить по первому закону Кирхгофа для узла N’ — рис. 11.22 (на рисунке изображен вспомогательный вектор тока, равный сумме токов I _А+ I _С):

Чем больше несимметрия фаз нагрузки, тем больше «уравнительный» ток I _N нулевого провода.

Соединение звездой с нулевым проводом повсеместно используется для электропитания жилых и общественных зданий, производственных приемников энергии и в других случаях с многочисленными приемниками, включаемыми и выключаемыми независимо друг от друга.

в) Соединение треугольником.
Если пренебречь сопротивлением соединительных проводов, то напряжения на фазах нагрузки равны линейным напряжениям трехфазного источника . Фазные токи при несимметричной нагрузке Z А B Z ВС Z С A определяются по закону Ома:

На рис. 11.25 показана векторная диаграмма токов при несимметричной активной нагрузке. Линейные токи определяются по первому закону Кирхгофа для узлов А, В и С рис. 11.17:

Как видно из векторной диаграммы (рис. 11.25), линейные токи не равны по модулю и смещены по фазе на углы, не равные 120°. В общем случае и фазные токи не равны по модулю и смещены по фазе на углы, не равные 120°.

Векторная диаграмма линейных токов показана на рис. 11.25.

г) Аварийные режимы в трехфазных цепях.
Частными случаями несимметричных режимов являются аварийные режимы в трехфазных цепях: обрывы нейтрального и линейных проводов, КЗ в фазах.
Абсолютно безопасными являются разрывы в фазах нагрузки, соединенной треугольником или звездой с нулевым проводом (отключения фаз)
Аварийными, пожароопасными являются КЗ фаз нагрузки таких соединений. Все другие случаи приводят к резкому изменению номинальных напряжений на фазах нагрузки и могут привести к аварийной ситуации. Обрыв нулевого провода несимметричной звезды был рассмотрен в примере 11.9.

Видео:Несимметричная нагрузка. Схема соединения "треугольник"Скачать

3.5. Несимметричные и аварийные режимы работы трехфазных цепей

Для соединения трехфазной цепи в звезду возможны следующие аварийные режимы работы:

1) обрыв фазы (рис. 3.10);

2) обрыв нулевого провода (рис. 3.11);

3) короткое замыкание фазы при обрыве нуля (рис. 3.12).

4) обрыв фазы и нуля, рис. 3.12.

Для соединения трехфазной цепи в треугольник возможны следующие аварийные режимы:

2) обрыв линейного провода.

Аварийные режимы в нагрузках соединенных звездой

1) При обрыве фазы А , работа нагрузкой не совершается, а остальные нагрузки () свои режимы работы не изменят (рис. 3.13): .

Если нагрузки связаны и является одним целым, то этот режим будет аварийным. Так, если эта нагрузка – асинхронный двигатель, то он будет в аварийном режиме и нулевой провод будет нагружен дополнительно (рис. 3.13):

2) Обрыв нулевого провода не всегда вызывает аварию в трехфазных цепях. Если нагрузка симметрична, то обрыв нулевого провода не изменит токов нагрузок, так как для симметричной нагрузки

.

Для несимметричных нагрузок , и поэтому такой режим может вызвать аварию.

Для того чтобы показать это, используем метод двух узлов:

Напряжение (рис. 3.14) не равно нулю, если нагрузки несимметричны. Фазные токи также будут неодинаковыми.

3) При коротком замыкании фазы А и обрыве нуля напряжение этой фазы равно нулю:, (рис. 3.15).

Нагрузка фазы В увеличится в раз:

.

Аналогично и в фазе С:

;

будет увеличен по отношению к исходному в раз.

4) Обрыв фазы и нулевого провода дает:

.

В оставшихся фазах токи будут одинаковыми, а напряжения на них будут зависеть от сопротивлений нагрузок (рис. 3.16).

Аварийные режимы в нагрузках соединенных треугольником

1) Обрыв фазы.

Ключ к1 замкнут, ключ к2 разомкнут (рис. 3.17). В этом режиме ток в фазе отсутствует, а остальные нагрузки работают как обычно (рис. 3.18). В таком аварийном режиме линейные токи фаз А и В соответствуют фазным токам, а линейный ток фазы С остается таким, каким был прежде.

2)

Обрыв линейного провода. Ключ к1 разомкнут и ключ к2 замкнут (рис. 3.19). Фаза нагрузки с своего режима не изменит, а фазы становятся последовательно соединенными и параллельно подключеннымик линейному напряжению фаз В, С (см. рис. 3.17), то есть цепь становитсяоднофазной. Топографическая и векторная диаграммы в этом случае могут иметьвид, как показано на рис.3.19.

Видео:Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

Трехфазные несимметричные цепи

Содержание:

Трехфазные несимметричные цепи:

Трехфазная цепь несимметрична, если комплексы сопротивлений ее фаз неодинаковы.

Несимметричной может быть действующая в цепи система э. д. с. (не равны модули э. д. с. или фазовые сдвиги между каждой парой э. д. с.). .
Для расчета несимметричной цепи применяются различные методы в зависимости от ее схемы и вида несимметрии.

Видео:Этому не учат, а стоило бы. Чем отличается звезда от треугольника? #звезда #треугольник #двигательСкачать

Расчет несимметричной трехфазной цепи при соединении источника и приемника звездой

На схеме (см. рис. 20.4) видно, что при соединении звездой трехфазная система представляет собой электрическую цепь с двумя узлами — нейтральными точками N и N’. Наиболее удобным методом расчета в данном случае является метод узлового напряжения.

Определение токов

Рассмотрим сначала общий случай расчета цепи с нулевым проводом, сопротивление которого Z_N. При этом сделаем некоторые упрощения: сопротивления линейных проводов и фаз источников будем полагать равными нулю. Если указанные сопротивления нельзя считать равными нулю, их можно отнести к приемнику, прибавив к сопротивлениям последнего по правилам сложения комплексов.
При таком упрощении потенциалы линейных зажимов источника и приемника (например, точек А и А’) можно считать одинаковыми.
Напряжение между нулевыми точками N и N’, или узловое напряжение

Смещение нейтрали

На рис. 21.1 изображена топографическая диаграмма цепи рис. 20.4, а при несимметричной нагрузке.

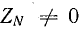
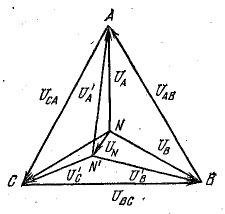
При наличии сопротивления в нулевом проводе () нулевая точка приемника на топографической диаграмме не совпадает с нулевой точкой источника. Поэтому напряжение U_N называют напряжением смещения нейтрали. Вследствие смещения нейтрали напряжения на фазах приемника оказываются неодинаковыми, несмотря на симметрию фазных напряжений источника (см. решение задачи 21.3).

Рис. 21.1. Топографическая диаграмма при несимметричной нагрузке (соединение звездой)

Из формулы (21.1) видно, что симметрия фазных напряжений на нагрузке, когда U_N = 0, достигается в двух частных случаях.
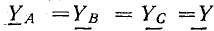
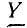
1. При симметричной нагрузке, когда комплексы проводимостей фаз равны: . В этом случае в числителе проводимость можно вынести за скобку, внутри которой складывается три вектора э. д. с. источника, равных по величине и сдвинутых по фазе на 120°; эта сумма равна нулю (см. рис. 20.8, б) и U_N = 0. Поэтому ток в нулевом проводе равен нулю [см. формулу (21.4)] и необходимость в этом проводе отпадает, а электроснабжение симметричных приемников осуществляется по трехпроводной системе.
2. В четырехпроводной системе, когда сопротивление нулевого провода равно нулю (Y_N = ∞.)

Роль нулевого провода

Нулевой провод является уравнительным. Потенциалы нейтрали источника и приемника с помощью этого провода принудительно уравнены, а поэтому звезда векторов фазных напряжений приемника точно совпадает со звездой фазных напряжений источника.

Четырехпроводная система применяется в электрических сетях с напряжением 380/220 В при электроснабжении от общего источника силовой (электродвигатели) и осветительной (электролампы) нагрузки.
При несимметричной нагрузке обрыв нулевого провода (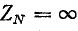) вызывает значительное изменение токов и фазных напряжений, что в большинстве случаев недопустимо. Поэтому в нулевой провод предохранители не устанавливаются.

Определение мощности

При несимметричной нагрузке нужно определить мощность каждой фазы. Например, для фазы А:

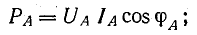
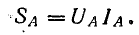
Аналогично определяются мощности других фаз.
Активная мощность всей трехфазной цепи равна сумме мощностей фаз:

Реактивная мощность цепи равна алгебраической сумме реактивных мощностей фаз:

В этой сумме реактивная мощность катушки считается положительной, а реактивная мощность конденсатора — отрицательной.

Задача 21.1.

При соединении звездой с нулевым проводом определить фазные напряжения и токи в приемнике энергии, сопротивления которого заданы комплексами:

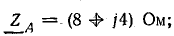
Действующая величина симметричной трехфазной системы э. д. с. 220 В. Сопротивление нулевого провода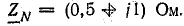
Построить векторную диаграмму.
Сопротивлениями линейных проводов и внутренними сопротивлениями источника э. д. с. пренебречь.
Решение. Схема, соответствующая условию задачи, показана на рис. 21.2, а.
Проводимости ветвей между узловыми точками NN’: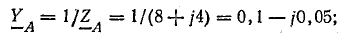

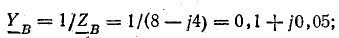
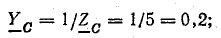
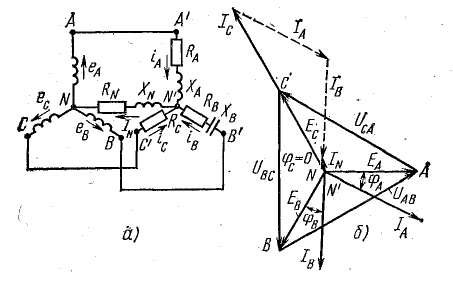
Рис. 21.2. К задаче 21.1

Комплексы э. д. с. источника:

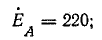
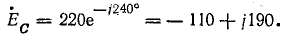
Узловое напряжение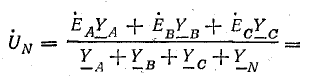



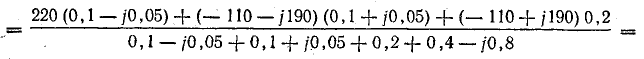
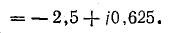
Фазные напряжения приемника: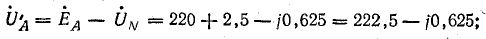



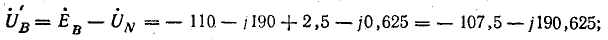
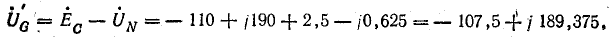
Токи в фазах и нулевом проводе: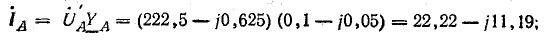




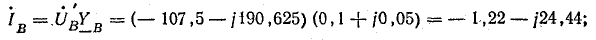
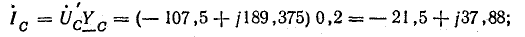
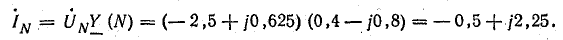
Векторная диаграмма напряжений и токов показана на рис. 21.2, б.

Задача 21.3.

Электрические лампы включены звездой в трехфазную сеть с линейным напряжением 380 В. В каждую фазу включены по 50 ламп с номинальной мощностью 60 Вт каждая, номинальным напряжением 220 В. Как изменяются фазные напряжения и токи при изменении нагрузки одной фазы от холостого хода до короткого замыкания при обрыве нулевого провода?
В каждом выбранном случае нагрузки построить векторную диаграмму, определить мощность всей трехфазной цепи.
Решение. Условию задачи соответствует схема рис. 21.3, а, на которой группа ламп в каждой фазе условно показана двумя лампами.
Оставляя постоянным число ламп в фазах В и С, будем менять его в фазе А. Подсчеты по условию задачи выполним для таких нагрузок в фазе А: 50, 25, 100 ламп, короткое замыкание, холостой ход.
1. При включении в каждую фазу по 50 одинаковых ламп нагрузка симметрична. Поэтому фазные напряжения на нагрузке равны фазным напряжениям в сети: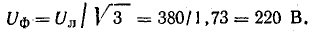

Напряжение на лампах равно номинальному. В этом случае лампы работают с номинальной мощностью.
Это даёт право определить фазные токи по заданной мощности ламп: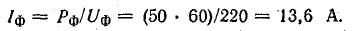

При соединении звездой I_Ф = I_Л, поэтому I_л = 13,6 А. Общая мощность трехфазной цепи
Р = ЗР_Ф = 3 • 60 • 50 = 9000 Вт.
2. В фазе А включено 25 ламп.
При несимметричной нагрузке напряжения на лампах отличаются от фазных напряжений в сети. Поэтому определить токи по заданной мощности ламп нельзя, так как действительная мощность ламп и фазные напряжения их неизвестны. При решении задачи будем считать, что сопротивление ламп в накаленном состоянии нити практически не меняется при некотором изменении их мощности.
Сопротивление лампы в номинальном режиме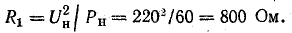

Сопротивление фаз В и С при включении 50 ламп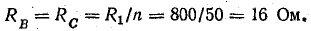

Сопротивление фазы А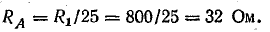

Комплексы фазных напряжений в сети:


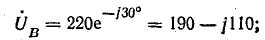
Проводимости ветвей:

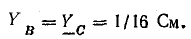
Смещение нейтрали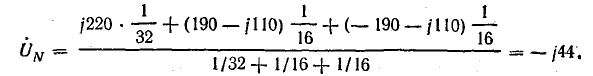

Напряжения фаз: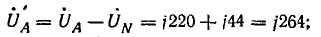



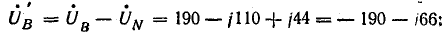
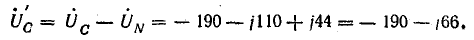
Токи в фазах: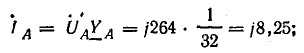



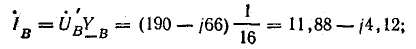
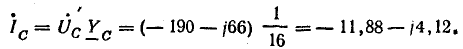
Мощность всех ламп в фазах: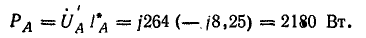



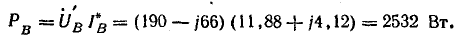
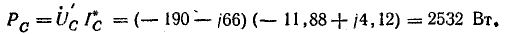
Мощность одной лампы: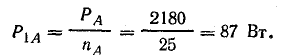



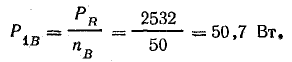
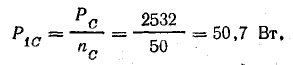
Общая мощность в трехфазной системе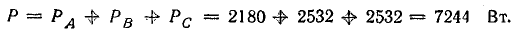

Векторная диаграмма напряжений для различной нагрузки фазы А показана на рис. 21.3, д.

Положение нулевой точки на диаграмме соответствует такой нагрузке фазы А: 1 — симметричная нагрузка (во всех фазах по 50 ламп); 2 — в фазе А 25 ламп; 3 — фаза А разомкнута (холостой ход); 4 — в фазе А 100 ламп; 5 — в фазе А короткое замыкание.

Выполните расчет трехфазной цепи для случаев нагрузки 3, 4, 5 подобно приведенному расчету для случая нагрузки 2, проверьте соответствие результатов расчета векторной диаграмме рис. 21.3, д.
Как видно, нулевая точка нагрузки при изменении проводимости фазы А перемещается на прямой АD, которая является перпендикуляром, опущенным из точки А к вектору линейного напряжения U_BC. При холостом ходе фазы А (обрыв линейного провода в этой фазе) нулевая точка перемещается в точку D и напряжения на двух других фазах U_B и U_C по величине оказываются равными половине линейного напряжения U_BC (рис. 21.3, б).

Рис. 21.3. К задаче 21.3

То же следует из схемы рис. 21.3, в. В рассматриваемом случае сопротивления фаз В и С оказываются включенными последовательно на линейное напряжение U_BC.

Сопротивления эти равны, поэтому линейное напряжение делится между двумя фазами поровну.

При коротком замыкании фазы А линейный провод этой фазы подводится непосредственно к нулевой точке нагрузки (рис. 21.3, г). Поэтому лампы, включенные в фазы В и С, оказываются под линейным напряжением.

Расчет несимметричной трехфазной цепи при соединении треугольником

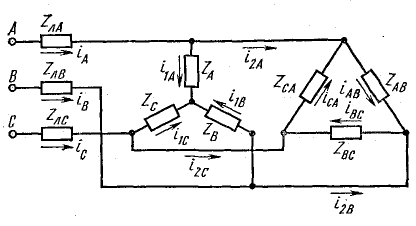
Трехфазная цепь при соединении приемника треугольником и любой схеме соединения фаз источника имеет разветвленную многоконтурную схему (см., например, рис. 20.8, а; 21.5).

Расчет такой цепи выполняется одним из известных методов с учетом состава ее элементов и схемы соединения.

Соединение источника и приемника треугольником

Расчет сложной цепи (см. рис. 20.8, а) значительно упрощается, если не принимать во внимание сопротивление проводов. В этом случае напряжения на фазах приемника равны соответствующим напряжениям источника и, как правило, представляют собой симметричную систему.
Если трехфазная система напряжений, приложенных к приемнику, известна, то фазные токи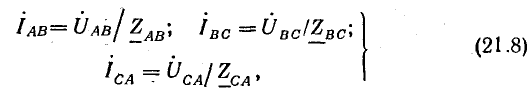
где 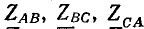— полные сопротивления фаз.
Линейные токи можно определить графически, как показано на рис. 21.4. Если задача решается в комплексной форме, линейные токи находят по формулам (20.7).

Мощность в несимметричной трехфазной цепи при соединении треугольником определяют по тем же формулам, что и при соединении звездой (21.6), (21.7).

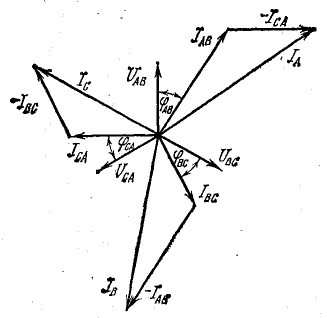
Рис. 21.4. Векторная диаграмма токов при несимметричной нагрузке (соединение треугольником)

Рис. 21.5. К вопросу о преобразовании треугольника сопротивлений в эквивалентную звезду в трехфазной цепи

Преобразование звезды и треугольника сопротивлений в трехфазных цепях

Расчет трехфазных цепей при смешанном соединении (звездой и треугольником), с учетом сопротивлений проводов линии представляет значительные трудности.

В этих случаях упрощения достигаются благодаря применению метода взаимного преобразования звезды и треугольника.
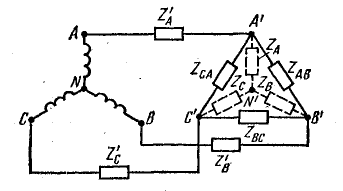
На рис. 21.5 приемник энергии соединен треугольником. С учетом сопротивлений проводов линии (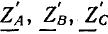) расчет такой цепи удобно выполнить, заменив треугольник сопротивлений эквивалентной звездой. Общее сопротивление фазы определяется сложением сопротивлений проводов линии и эквивалентной звезды приемника.

Если в ходе расчета схемы со смешанным соединением приемников — звездой и треугольником (рис. 21.6) — необходимо определить общее сопротивление фазы, это делается преобразованием звезды в треугольник или треугольника в звезду.
При симметричной нагрузке можно преобразовать треугольник в звезду, а затем две звезды заменить одной. Последняя операция возможна только при симметричной нагрузке, когда фазные напряжения у этих «звезд» одинаковы (смещение нейтрали отсутствует). При несимметричной нагрузке звезду следует преобразовать в эквивалентный треугольник, а затем сложением соответствующих проводимостей определить общую проводимость каждой фазы.

Рис. 21.6. к расчету трехфазной цепи при соединении приемников звездой и треугольником

Если в последнем случае требуется учесть сопротивление проводов, то общий треугольник еще раз приходится преобразовать в звезду и к сопротивлениям звезды прибавить сопротивления проводов линии.

Задача 21.4.

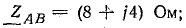
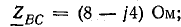
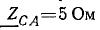
Сопротивления фаз приемника подключены треугольником к трехфазному генератору, обмотки которого также соединены треугольником. Действующие значения симметричной системы э. д. с. генератора 220 В. Пренебрегая сопротивлениями линейных проводов и обмоток генератора, определить фазные и линейные токи, активную, реактивную и полную мощности каждой фазы и всей цепи. Построить векторную диаграмму.
Решение. Схема рис. 20.8, а соответствует условию задачи. Если сопротивления линейных проводов и обмоток генератора считать равными нулю, то фазные напряжения приемника равны соответствующим э. д. с.:

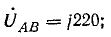
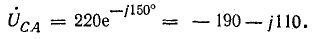
Фазные токи в приемнике: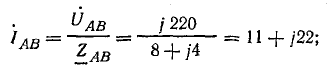



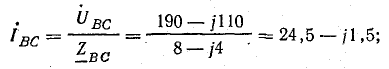
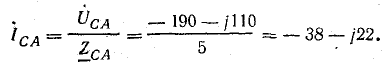
Линейные токи: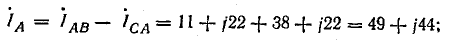



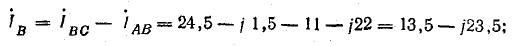
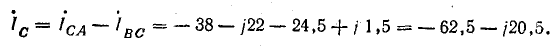
Сумма линейных токов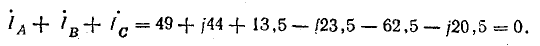

Равенство нулю суммы линейных токов является общим свойством трехфазных трехпроводных цепей при соединении звездой и треугольником при симметричной и несимметричной нагрузках.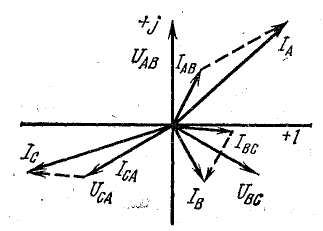

Рис. 21.7. К задаче 21.4

Рис. 21.8. К задаче 21.5

Мощности фаз: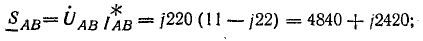



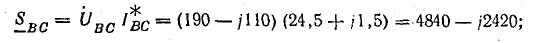
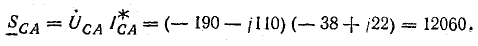
Общая мощность системы:
активная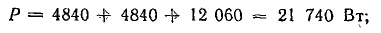

реактивная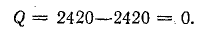

Векторная диаграмма построена на рис. 21.7.

Задача 21.5.

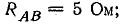
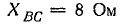
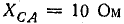
Приемник электрической энергии, соединенный треугольником, включен в сеть с линейным напряжением 120 В. Сопротивления фаз: (инд.); (емк.).
Начертить схему по условию задачи. Определить фазные и линейные токи, активную, реактивную и полную мощности в каждой фазе и всей цени. Построить векторную диаграмму.
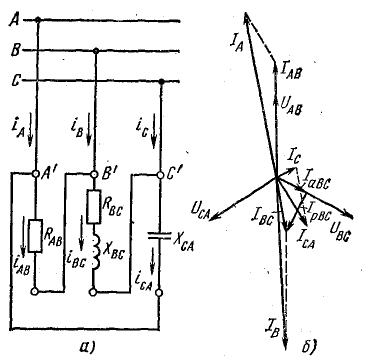
Решение. Схема цепи изображена на рис. 21.8, а.
Решим задачу без применения комплексных чисел. Токи в фазах: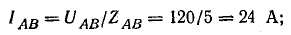



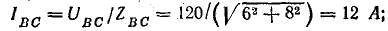
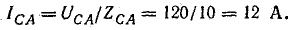
Линейные токи определим графически с помощью векторной диаграммы. Для этого найдем активные и реактивные токи фаз.
В фазе АВ включено активное сопротивление, поэтому

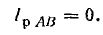
В фазе ВС последовательно соединены R и Х_L, поэтому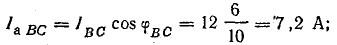


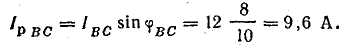
В фазе CA включено емкостное сопротивление, следовательно,

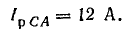
Векторная диаграмма цепи показана на рис. 21.8, б. Для определения линейных токов постройте векторную диаграмму на листе миллиметровой бумаги в масштабах: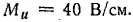
Линейные токи: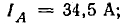
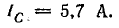
Мощности фаз:
активные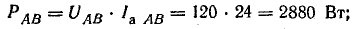

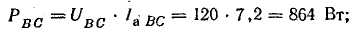
реактивные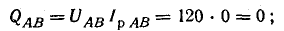



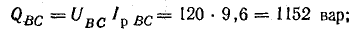
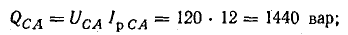
полные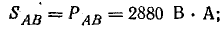



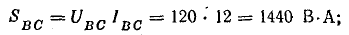
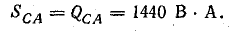
Мощность всей цепи:
активная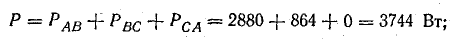

реактивная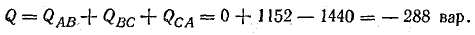

Знак минус указывает на емкостный характер реактивной мощности цепи.

Симметричные составляющие несимметричной трехфазной системы

Несимметричную трехфазную систему токов (напряжений или других синусоидальных величин) можно представить в виде суммы трех симметричных систем.

Разложение несимметричной системы векторов на симметричные составляющие применяется для расчета и анализа несимметричных режимов в трехфазных цепях: при симметричной нагрузке, но несимметричной системе э. д. с., при однофазных и двухфазных коротких замыканиях, при обрыве линейных проводов в цепях с симметричной системой э. д. с.

Комплексы симметричных составляющих

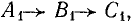
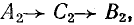
Первая симметричная система имеет прямую последовательность фаз ( рис. 21.9, а), вторая — обратную ( рис. 21.9, б). Третья система, называемая системой нулевой последовательности, состоит из трех равных величин, совпадающих по фазе ( рис. 21.9, в).

Рис. 21.9. Симметричные составляющие несимметричной системы

Система величин:
прямой последовательности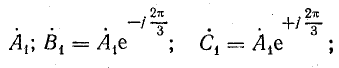

обратной последовательности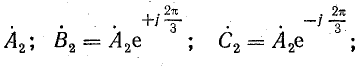

нулевой последовательности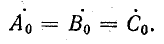

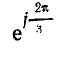
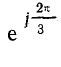
Умножение на означает поворот вектора на 120″ против движения часовой стрелки. Обозначим через а и будем называть это выражение поворотным множителем.
Поворот вектора против часовой стрелки на 240° можно выразить умножением его на а 2 .
Умножение вектора на а 3 не меняет его положения: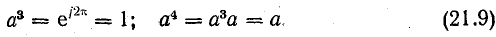

С помощью поворотного множителя а системы прямой и обратной последовательности можно записать так: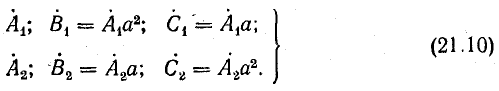

Сумма синусоидальных величин симметричной системы равна нулю, поэтому

Разложение несимметричной системы на симметричные составляющие

Выразим комплексы несимметричной системы через симметричные составляющие: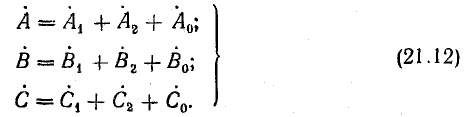

Если из этой системы уравнений можно однозначно определить симметричные составляющие через известные величины 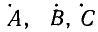несимметричной системы, то этим будет доказана возможность разложения несимметричной системы на три симметричные — прямой, обратной и нулевой последовательности.
Используя выражения (21.10), запишем систему уравнений (21.12) в таком виде: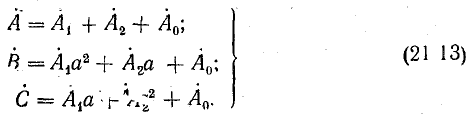

Решение системы уравнений (21.13) позволяет найти симметричные составляющие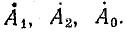
Сложим уравнения: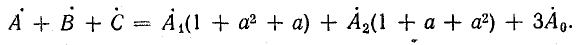

Учитывая формулу (21.11), найдем

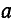
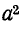
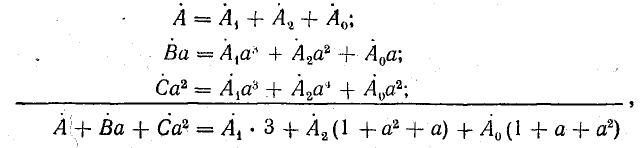
Умножим второе уравнение в системе (21.13) на , а третье — на и сложим все уравнения:

откуда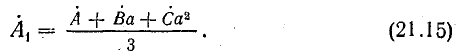

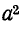
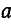
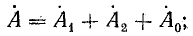
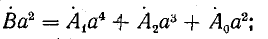
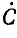
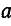
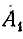
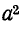
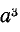
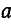
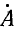
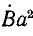
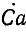
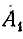
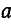
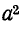
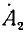
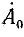
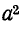
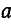
Умножим второе уравнение в системе (21.13) на , а третье на и сложим все уравнения:


= + ₊

+ + = (1 + + ) + • 3 + (1 + + )
откуда
= (21.16)

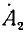
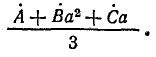
Свойства трехфазных цепей

Отметим некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений.

Степень несимметрии линейных напряжений оценивается коэффициентом несимметрии, т.е. отношением составляющей обратной последовательности напряжений к составляющей прямой последовательности.
ε = 100 • U_оп/U_пп.
Отсюда следует, что ток в нулевом проводе можно найти, если утроить величину составляющей тока нулевой последовательности.
В трехпроводной системе сумма линейных токов равна нулю. Из формулы (21.14) следует, что линейные токи в этом случае не содержат составляющей нулевой последовательности. Это справедливо и для линейных напряжений трехфазной системы, сумма которых тоже равна нулю.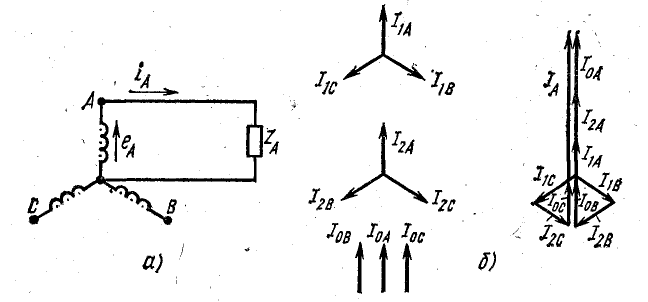

Рис. 21.10. Симметричные составляющие токов трехфазной цепи при разомкнутых двух фазах

Отсутствие тока в одной или двух фазах при несимметричном режиме означает, что сумма трех симметричных составляющих токов в этих фазах равна нулю.
Например, на схеме рис. 21.10, а фазы В и С разомкнуты. Поэтому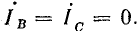
Согласно формулам (21.14) — (21.16), симметричные составляющие токов имеют следующие выражения:
прямой последовательности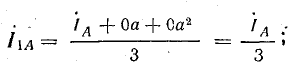

обратной последовательности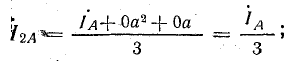

нулевой последовательности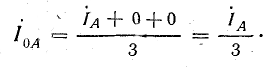

На рис. 21.10, б показаны симметричные составляющие прямой, обратной и нулевой последовательности и их геометрическое сложение; в результате сложения получаем: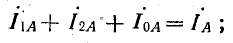

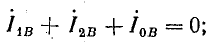
Задача 21.8.

В результате неправильной маркировки концов обмоток трехфазного трансформатора (начало фазы А вторичной обмотки помечено как конец) система линейных напряжений несимметрична. Определить симметричные составляющие линейных напряжений при соединении звездой, если фазные напряжения во вторичной обмотке 220 В.
Решение. Запишем комплексы фазных напряжений во вторичной обмотке: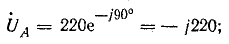



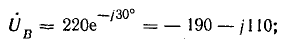
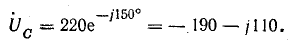
Вектор напряжения 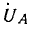в соответствии с условием задачи повернут на 180°.
Комплексы линейных напряжений: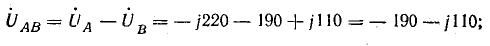



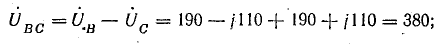
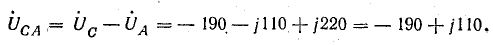
Составляющие:
нулевой последовательности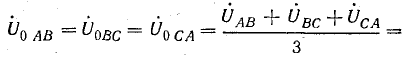


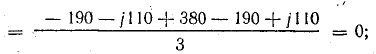
прямой последовательности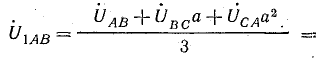




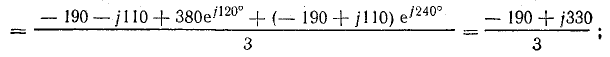
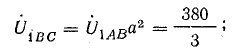
обратной последовательности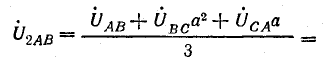

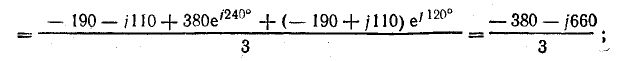
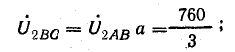
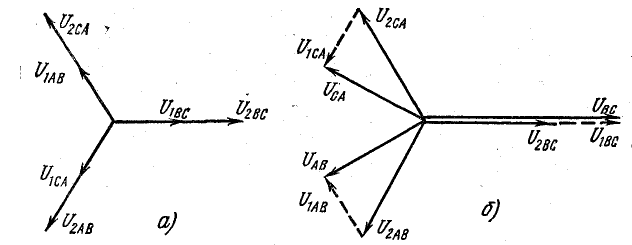
Рис. 21.11. К задаче 21.8

На рис. 21.11, а, б показаны векторы систем прямой и обратной последовательности и их сумма — система трех исходных векторов линейных напряжений.

Задача 21.9.

Трехфазный электродвигатель, включенный в сеть с линейным напряжением 380 В при соединении звездой, имеет мощность на валу Р₂ = 14 кВт; соsφ = 0,8; к. п. д. η = 0,85.
Определить симметричные составляющие токов в обмотке двигателя при обрыве линейного провода в фазе В.
Решение. При нормальной работе ток в фазе двигателя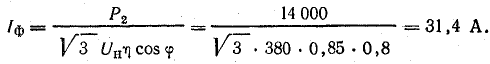

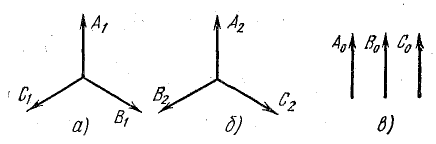
При симметричной системе напряжений токи в фазах двигателя образуют симметричную систему (рис. 21.12, а). При обрыве линейного провода В векторная диаграмма фазных напряжений и токов показана на рис. 21.12, б.
Ток в фазах В равен нулю (I_B = 0).
Токи в фазах А и С равны по величине, но находятся в противофазе: I_А = I_C.
Для определения величины токов I_А и I_C найдем расчетное сопротивление фазы двигателя при нормальном режиме, которое будем считать неизменным: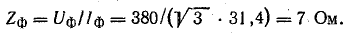

При обрыве линейного провода фазы В обмотки двух других фаз двигателя с одинаковым сопротивлением включены последовательно на линейное напряжение U_CA. Поэтому ток в фазах А и С

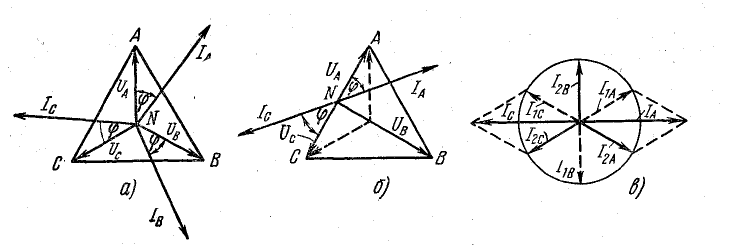
Рис. 21.12. к задаче 21.9

Выразим токи в комплексной форме, полагая ток I_A совпадающим с положительным направлением действительной оси:

Токи:
нулевой последовательности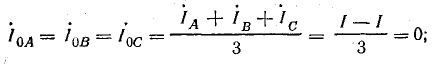

прямой последовательности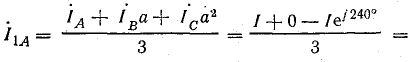



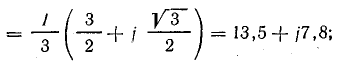
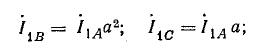
обратной последовательности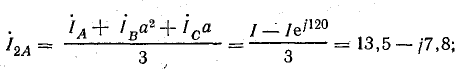

На рис. 21.12, в изображены симметричные составляющие токов в двигателе при обрыве фазы.

Несимметричный режим работы трехфазной цепи

Несимметрия в трехфазной цепи может быть вызвана различными причинами: 1) неодинаковым сопротивлением фаз (несимметричная нагрузка); 2) несимметричным коротким замыканием (например, между двумя фазами или фазой и нейтралью); 3) размыканием фазы; 4) неравенством э. д. с. и т. п.

Расчет токов и напряжений в трехфазной цепи при несимметричном режиме может производиться теми же

методами, которые применяются для расчета однофазных цепей.

Рассмотрим несколько простейших вариантов (без взаимной индукции между фазами).

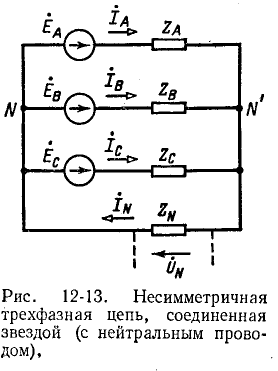
1. Несимметричная трехфазная цепь, соединенная звездой, с нейтральным проводом (рис. 12-13).

Несимметричная трехфазная цепь, показанная на рис. 12-13, может рассматриваться как трехконтурная цепь с тремя э. д. с. Такая цепь может быть рассчитана методами контурных токов, узловых напряжений и другими. Поскольку в схеме имеются только два узла, наиболее целесообразно в данном случае определить узловое напряжение (напряжение смещения) между нейтральными точками N’ и N по формуле,

где 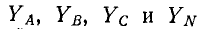— проводимости соответствующих ветвей.

После этого найдем токи:

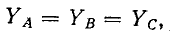
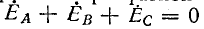
В симметричной трехфазной цепи и поэтому при узловое напряжение равно нулю.

Стучаю размыкания какой-либо фазы или нейтрального провода соответствует равенство нулю проводимости данной фазы или нейтрального провода. j

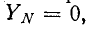
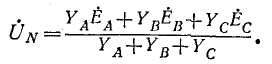
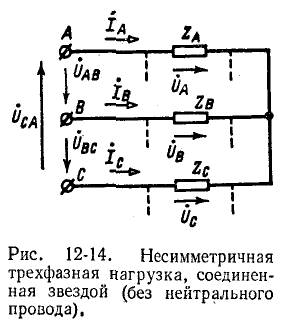
При отсутствии нейтрального провода, полагая в (12-1), имеем:

2. Несимметричная трехфазная нагрузка, соединенная звездой (без нейтрального провода), с заданными линейными напряжениями на выводах (рис. 12-14).

Если заданы линейные напряжения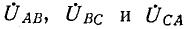на выводах нагрузки, соединенной звездой, то токи в фазах звезды определяются следующим образом.

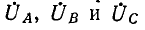
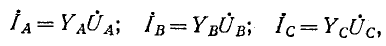
Обозначив фазные напряжения на выводах нагрузки через(рис. 12-14), получим

где 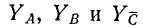— проводимости фаз нагрузки.

Равенство нулю суммы токов трех фаз записывается в виде:

Фазные напряжения могут быть выражены через и заданные линейные напряжения: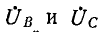

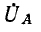
Подстановка (12-3) в (12-2) дает:

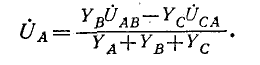
Круговой заменой индексов (с порядком следования АВСА и т. д.) находятся: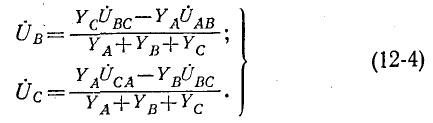

По фазным напряжениям нагрузки находятся фазные токи.

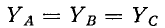
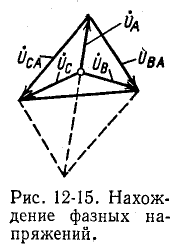
В Случае симметричной нагрузки вектор фазного напряжения равен одной трети диагонали параллелограмма, построенного на соответствующих линейных напряжениях. Фазные напряжения в этом случае определяются векторами, соединяющими центр тяжести треугольника напряжений (точка пересечения медиан) с вершинами треугольника.

На рис. 12-15 построение сделано для фазы А по формуле (12-4)1

В качестве примера рассмотрим схему фазоуказателя, используемую для определения чередования фаз по времени, состоящую из конденсатора и двух одинаковых электрических ламп, соединенных звездой.

Положим, что конденсатор присоединен к фазе А, лампы — к фазам В и С; емкостное сопротивление конденсатора берется равным по модулю сопротивлению лампы, т. е. 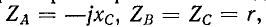причем

Неравенство напряжений на лампах проявится в том, что накал ламп будет разным.

1 Для определения чередования фаз на практике обычно пользуются специальным прибором, в котором создается вращающееся магнитное поле, увлекающее за собой диск в ту или другую сторону.

Отношение напряжений согласно выведенным выше выражениям (12-4) равно при симметрии линейных напряжений:

Следовательно, лампа, присоединенная к фазе В (т. е. к фазе, опережающей ту, к которой присоединена вторая лампа), будет светить ярко, а лампа, присоединенная к отстающей фазе, — тускло.

Вместо конденсатора можно применить индуктивную катушку, подобрав ее индуктивное сопротивление приблизительно равным по модулю сопротивлению лампы. В этом случае ярче будет светить лампа, присоединенная к отстающей фазе. Эти соотношения также могут быть получены непосредственно из векторной диаграммы.

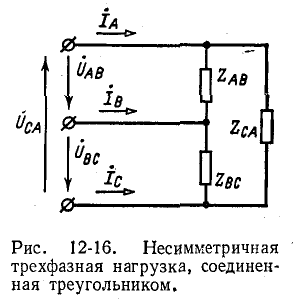
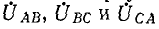
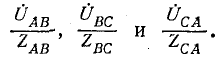
3. Несимметричная трехфазная нагрузка, соединенная треугольником, с заданными напряжениями на выводах Рис. 12-16. Несимметричная (рис. 12-16). Если на выводах несимметричной трехфазной нагрузки, соединенной треугольником, заданы линейные напряжения (рис. 12-16), то токи в сопротивлениях нагрузки равны:

Токи в линии определяются как разности соответствующих токов нагрузки, например: 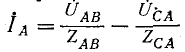и т. д.

Если на выводах несимметричной трехфазной нагрузки, соединенной треугольником, заданы фазные напряжения 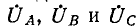источника, соединенного в звезду, то линейные напряжения на выводах нагрузки находятся как разности соответствующих фазных напряжений, в результате чего задача сводится к только что рассмотренному случаю(рис. 12-16).
Пример 12-2. Сопротивления фаз нагрузки, соединенной звездной

Сопротивление нейтрального провода

Напряжения на цепи представляют собой симметричную звезду:

Требуется определить фазные напряжения нагрузки.

Проводимости фаз нагрузки и нейтрального провода

На основании формулы (12-1)

Искомые фазные напряжения нагрузки:

Мощность несимметричной трехфазной цепи

Пользуясь комплексной формой записи мощности, можно написать общее выражение для мощности трехфазной цепи:

Действительная часть этого выражения представляет собой активную мощность

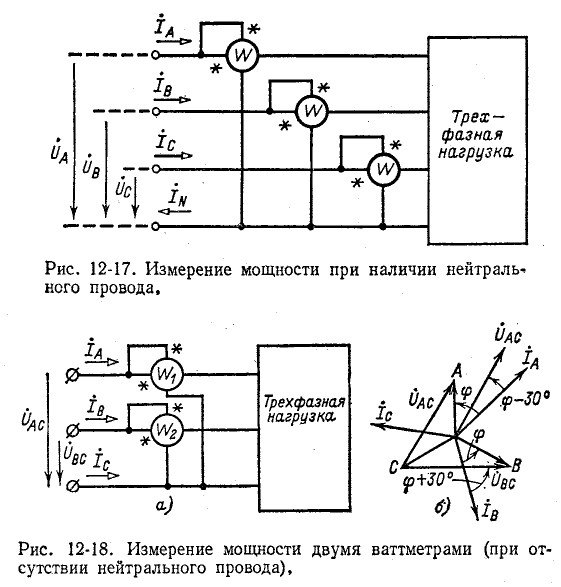
Суммарная активная мощность, потребляемая несимметричной трехфазной цепью, может быть в соответствии с этим измерена при помощи трех ваттметров, включенных на подведенные к данной цепи фазные напряжения относительно нейтрали и одноименные с ними токи. Активная мощность равна сумме показаний трех ваттметров. Такой метод измерения применяется при наличии нейтрального провода (рис. 12-17) или искусственно созданной нейтральной точки.

В случае отсутствия нейтрального провода измерение может быть произведено с помощью двух ваттметров

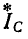
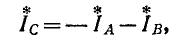
(рис. 12-18). В этом случае выражение (12-5) преобразуется следующим образом: исключая ток с помощью условия
получаем:

или

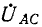
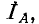
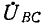
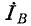
В соответствии с (12-6) при измерении активной мощности двумя ваттметрами к одному из них подводятся напряжение и ток а ко второму — напряжение и ток (рис. 12-18, а). Показания ваттметров складываются алгебраически.

Круговой заменой А, В. и С в выражении (12-6) можно получить выражения для других равноценных вариантов включения двух ваттметров.

Следует иметь в виду’, что если стрелка одного ваттметра отклоняется по шкале в обратную сторону, то, изменив направление напряжения или тока, подводимого к данному ваттметру, записывают полученное показание со знаком минус. При симметричном режиме работы трехфазной цепи такое положение имеет место при

что видно непосредственно из векторной диаграммы (рис. 12-18, б).

При симметричном режиме показания двух ваттметров в схеме рис. 12-18, б будут следующие:

Сумма и разность показаний ваттметров соответственно равны:

Следовательно, при симметричном режиме работы трехфазной цепи тангенс угла сдвига фаз может быть вычислен по формуле

• Вращающееся магнитное поле
• Электрические цепи синусоидального тока
• Электрические цепи несинусоидального тока
• Несинусоидальный ток
• Метод симметричных составляющих
• Цепи периодического несинусоидального тока
• Резонанс токов
• Трехфазные симметричные цепи

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

💡 Видео

Трехфазные цепи. Схема соединения "ЗВЕЗДА"Скачать

Мощность трехфазного напряжении при подключении нагрузки звездой и треугольникомСкачать

Соединение звезда и треугольник. Различие между нимиСкачать

Соединение трехфазных цепей звездой и треугольникомСкачать

Трёхфазный переменный ток. Соединение "звезда" и "треугольник"Скачать

Лекция 25. Преобразование звезды в треугольник.Скачать

Соединение треугольникомСкачать

Трехфазная система. Анимация электрических процессовСкачать

#012. Режим переключения "Звезда"-"Треугольник". Часть 1.Скачать

Симметричная нагрузка в трехфазной цепиСкачать

Что такое звезда и треугольник в трансформаторе?Скачать

Треугольник в звезду и наоборот.Скачать

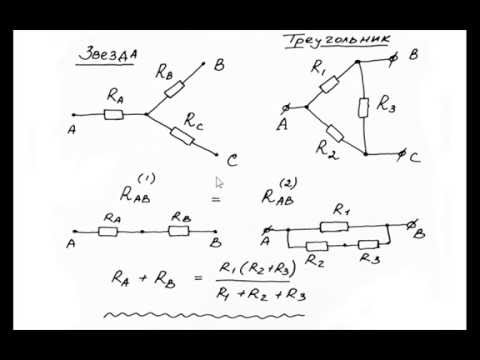
Звезда,треугольник соединение сопротивленийСкачать

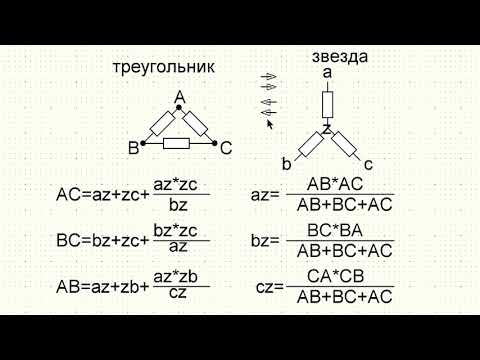
Для чего нужен ноль? Почему у трехфазного двигателя нет нуля и куда девается ток?Скачать

#001."Звезда" или "Треугольник"?Скачать

Электрика для начинающих#10 Автоматика "Звезда-Треугольник". Принцип работы. Детальный разбор схемы.Скачать