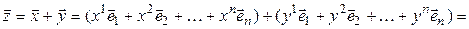Доказательства свойств координат векторов (6 видео)

Координаты вектора в математике

Координаты вектора ― это коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.

Содержание:

Содержание

Координаты вектора
Свойства координат вектора
Свойства координат векторов
Операции над векторами и их свойства: сложение и умножение
Сложение двух векторов
Сложение нескольких векторов
Умножение вектора на число
Свойства операций над векторами
📸 Видео

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Координаты вектора

Для введения понятия координат вектора следует рассмотреть возможность разложения вектора по осям координат. Мы хотим каждый вектор задать парой чисел — проекциями этого вектора на оси координат. При таком подходе действия над векторами можно свести к действиям с парами чисел.

Определим проекции вектора на координатную ось. Пусть задана координатная ось Ох. Единичный отрезок ОЕ теперь будем считать единичным вектором , т. е. вектором, длина которого равна 1 (рис. 2.506).

Возьмем любой вектор и отложим его от некоторой точки А:

Спроектируем точки А и В на ось Ох. Получим точки и составляющую вектора по оси Ох (рис. 2.507). Ее длина со знаком «плюс» или «минус» и называют проекцией вектора на ось Ох.

Определение. Проекцией вектора на ось Ох называют длину его составляющей по этой оси, взятую со знаком «плюс» или «минус». При этом берется знак «плюс», если направление вектора совпадает с направлением оси Ох, и знак «минус», если эти направления противоположны. Если = 0, т. е.

Проекция точки — точка, проекция отрезка — отрезок (или точка), а проекция вектора — число.

Вектор получается из коллинеарного ему единичного вектора умножением на . При этом если сонаправлен с , то Если же противоположно направлен , то

Следовательно, имеет место равенство

Можно доказать следующие свойства проекций векторов на ось.

1. Равные векторы имеют равные проекции на заданную ось.

2. При сложении векторов их проекции на ось складываются.

3. При умножении вектора на число его проекция умножается на это число.

Прежде чем ввести понятие координат вектора, докажем теорему.

Теорема 6. Пусть на плоскости введена прямоугольная система координат с единичными векторами координатных осей Ох и Оу. Пусть — некоторый вектор, а — его проекции на оси координат. Тогда вектор единственным образом представляется в виде (рис. 2.508).

Выше получена формула для разложения вектора а по векторам (с учетом обозначения): .

Пару чисел называют координатами вектора в данной системе координат.

Координаты вектора в пространстве определяются так же, как на плоскости. Справедлива следующая теорема.

Теорема 7. Пусть в пространстве введена прямоугольная система координат с единичными векторами координатных осей Ох, Оу, Oz. Тогда вектор единственным образом представляется в виде (рис. 2.509).

Числа называются координатами вектора относительно векторов, которые называются базисными векторами или, короче, базисом.

Введенные координаты вектора позволяют получить формулу длины вектора.

Рассмотрим рисунок 2.508.

1. Если точка А не лежит на координатных осях, то треугольник прямоугольный.

2. (1, теорема Пифагора).

3. Так как то получаем, что (2).

4. Но поэтому

(3, 4).

Формула справедлива и в тех случаях, когда точка А лежит на какой-то оси координат.

Свойства координат вектора

В курсе геометрии нам практически не приходится работать с векторами в координатах (это приходится делать в курсе физики). Можно доказать различные свойства координат вектора:

1. Координаты равных векторов соответственно равны. Обратно: векторы, имеющие соответственно равные координаты, равны.

2. При сложении векторов их соответствующие координаты складываются. А именно, если

3. При умножении вектора на число его координаты умножаются на это число. А именно, если

Координаты вектора связаны с координатами точки по следующему правилу: чтобы найти координаты вектора, нужно от координат конца вектора отнять координаты начала вектора.

В частности, если вектор отложен от начала координат, то координаты вектора равны координатам его конца.

Возьмем в пространстве некую прямоугольную систему координат с началом в точке О и координатными осями х, у, z (рис. 2.510). Пусть А, В, С — точки с единичными координатами на этих осях, т. е. А(1, 0, 0), В(0, 1, 0), С(0, 0, 1).

Тогда векторы — это направляющие единичные векторы координатных осей х, у, z.

Возьмем любую точку М(х, у, г), и пусть — ее радиус-вектор.

Теорема 8. Координаты точки М соответственно равны координатам ее радиус-вектора относительно базиса .

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Видео:9 класс, 2 урок, Координаты вектораСкачать

Свойства координат векторов

Дата добавления: 2015-08-06 ; просмотров: 1918 ; Нарушение авторских прав

1º. Если все координаты вектора в некотором базисе равны нулю, то этот вектор – нулевой.

►Доказательство очевидным образом вытекает из аксиом линейного пространства и следствий к ним: . ◄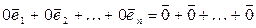

2º. Все координаты нулевого вектора в любом из базисов равны нулю.

( ) – (3.22) базис линейного пространства ;

(3.23)

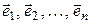
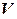
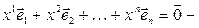
разложение нулевого вектора по базису (3.22). В силу линейной независимости (3.22) из (3.23) вытекает, что . ◄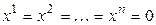

3º. Координаты вектора в данном базисе определяются однозначно.

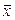
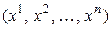
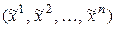
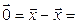
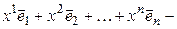
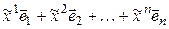
►Пусть некоторый вектор в базисе (3.22) имеет два разных набора координат: и . Тогда

( ) =

= [аксиомы 1*, 2* и 6* из определения линейного пространства] =

= (3.24)

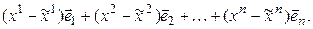
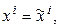
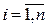
Равенство (3.24) – это разложение по базису (3.22) нулевого вектора, и поэтому все коэффициенты разложения равны нулю, следовательно, , что противоречит условию. ◄

4º. При сложении векторов их соответствующие координаты складываются.

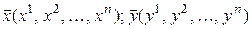
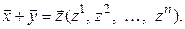
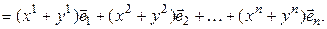
► Пусть заданы векторы своими координатами в базисе (3.22) и пусть Тогда

(3.25)

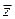
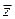
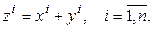
Равенство (3.25) – это разложение вектора по базису (3.22), следовательно, коэффициенты разложения – координаты вектора в базисе (3.22). В силу единственности координат вектора в данном базисе получаем: ◄

5º. При умножении вектора на число все его координаты умножаются на это число.

Свойство доказывается точно так же, как и предыдущее, это вы можете сделать самостоятельно.

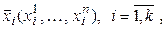
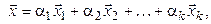
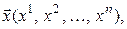
Следствие. Координаты линейной комбинации векторов равны таким же (с такими же коэффициентами) линейным комбинациям соответствующих координат слагаемых, т. е. если и то

Видео:Координаты вектора. 9 класс.Скачать

Операции над векторами и их свойства: сложение и умножение

Прежде чем приступить к тематике статьи, напомним основные понятия.

Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.

Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.

Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.

Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Сложение двух векторов

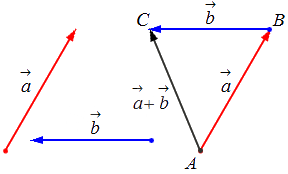
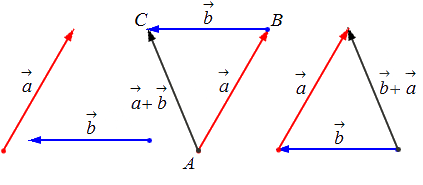
Исходные данные: векторы a → и b → . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор A B → , равный вектору а → ; из полученной точки undefined – вектор В С → , равный вектору b → . Соединив точки undefined и C , получаем отрезок (вектор) А С → , который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.

Геометрически сложение векторов выглядит так:

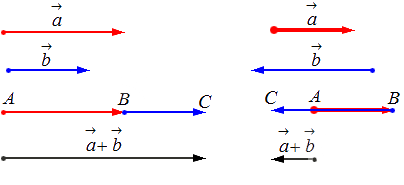
— для неколлинеарных векторов:

— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Сложение нескольких векторов

Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.

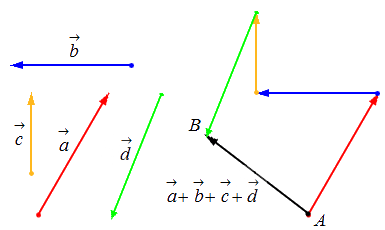
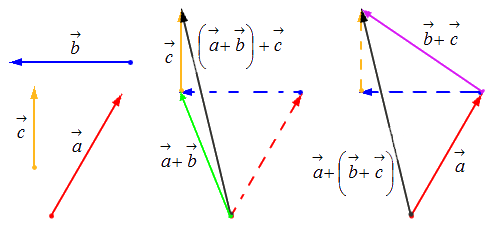
Исходные данные: векторы a → , b → , c → , d → . Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a → ; затем от конца полученного вектора откладывается вектор, равный вектору b → ; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B , а полученный отрезок (вектор) A B → – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .

Геометрически оно выглядит следующим образом:

Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a → и b → есть сумма векторов a → и — b → .

Видео:Скалярное произведение векторов. 9 класс.Скачать

Умножение вектора на число

Чтобы произвести действие умножения вектора на некое число k , необходимо учитывать следующие правила:
— если k > 1 , то это число приведет к растяжению вектора в k раз;
— если 0 k 1 , то это число приведет к сжатию вектора в 1 k раз;
— если k 0 , то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
— если k = 1 , то вектор остается прежним;
— если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.

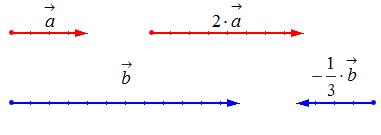
Исходные данные:
1) вектор a → и число k = 2 ;
2) вектор b → и число k = — 1 3 .

Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Свойства операций над векторами

Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.

Исходные данные: векторы a → , b → , c → и произвольные действительные числа λ и μ .

Свойство коммутативности: a ⇀ + b → = b → + a → .
Свойство ассоциативности: ( a → + b → ) + c → = a → + ( b → + c → ) .
Свойство использования нейтрального элемента по сложению (нулевой вектор 0 → ⃗). Это очевидное свойство: a → + 0 → = a →
Свойство использования нейтрального элемента по умножению (число, равное единице): 1 · a → = a → . Это очевидное свойство, не предполагающее никаких геометрических преобразований.
Любой ненулевой вектор a → имеет противоположный вектор — a → и верным является равенство: a → + ( — a → ) = 0 → . Указанное свойство — очевидное.
Сочетательное свойство операции умножения: ( λ · µ ) · a → = λ · ( µ · a → ) . Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
Первое распределительное свойство (очевидно): ( λ + µ ) · a → = λ · a → + µ · a → .
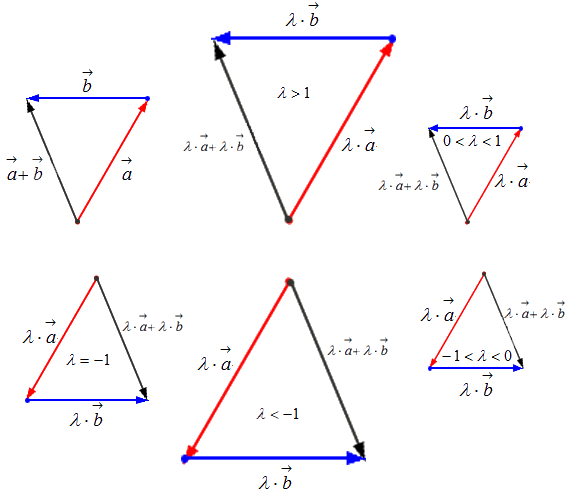
Второе распределительное свойство: λ · ( a → + b → ) = λ · a → + λ · b → .
Геометрически это свойство определяется подобием треугольников:

Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.

Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.

Задача: упростить выражение a → — 2 · ( b → + 3 · a → )
Решение
— используя второе распределительное свойство, получим: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · ( 3 · a → )
— задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a → — 2 · b → — 2 · ( 3 · a → ) = a → — 2 · b → — ( 2 · 3 ) · a → = a → — 2 · b → — 6 · a →
— используя свойство коммутативности, меняем местами слагаемые: a → — 2 · b → — 6 · a → = a → — 6 · a → — 2 · b →
— затем по первому распределительному свойству получаем: a → — 6 · a → — 2 · b → = ( 1 — 6 ) · a → — 2 · b → = — 5 · a → — 2 · b → Краткая запись решения будет выглядеть так: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · 3 · a → = 5 · a → — 2 · b →
Ответ: a → — 2 · ( b → + 3 · a → ) = — 5 · a → — 2 · b →