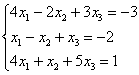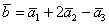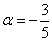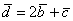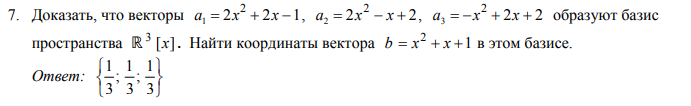Доказать что векторы образуют базис в r3 найти координаты вектора

Решение:
Записываем матрицу перехода А:

и находим ее определитель
0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f₁ , f₂ , f₃ линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R 3 .
Находим обратную матрицу А -1 .
Транспонированная матрица:

Обратная матрица А -1

Находим координаты вектора х относительно нового базиса.

Пример №1 . Даны векторы a, b, c и d . Установить, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 — β*2 — γ*2 = 3
α*1 + β*1 + γ0 = 1 т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c :
d = 1/2a + 1/2b — 3/2c

Пример №2 . Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе:

Пример №3 . Даны два линейных преобразования:
х’₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃, х»₁ = b₁₁x’₁ + b₁₂x’₂ + b₁₃x’₃,
х’₂ = a21x1 + a22x2 + a23x3, х»₂ = b₂₁x’1 + b₂₂x’₂ + b₂₃x’₃,
х’₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃, х»₃ = b₃₁x’₁ + b₃₂x’₂ + b₃₃x’₃,
Средствами матричного исчисления найти преобразование, выражающее х»₁, x»₂, x»₃ через х₁, х₂, х₃.
х’₁ = 4x₁ + 3x₂ + 5x₃, х»₁ = — x’₁ + 3x’₂ — 2x’₃,
х’₂ = 6x₁ + 7x₂ + x₃, х»₂ = — 4x’₁ + x’₂ + 2x’₃,
х’₃ = 9x₁ + x₂ + 8x₃, х»₃ = 3x’₁ — 4x’₂ + 5x’₃,
Решение. Используя калькулятор, получаем:
Обозначим:

Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 — 1*1) — 6*(3*8 — 1*5) + 9*(3*1 — 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1 : A -1 ·A·X = A -1 ·B, тогда получим E·X = A -1 ·B, или X = A -1 ·B.
Найдем обратную матрицу A -1 .

Матрицу Х ищем по формуле:

Пример №4 . В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC ;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e ₁= AB , e ₂= AC , e ₃= AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN , где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису ( e ₁, e ₂, e ₃)

Решение. Пункты (а-д) решаются через онлайн калькулятор.

Задание 1 . Разложить вектор d =(8;-5) по векторам a =(1;-2) и b =(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (, то есть соответствующие координаты этих векторов не пропорциональны).
Следовательно, вектор d = α a +β b , где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид
Решим полученную систему уравнений.

Видео:Как разложить вектор по базису - bezbotvyСкачать

Доказать, что 3 вектора образуют базис трёхмерного пространства и найти координаты 4-го вектора в данном базисе

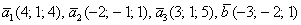
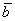
Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе.

Решение: Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора вполне могут образовывать новый базис. И первый этап полностью совпадает с решением Примера 6, необходимо проверить, действительно ли векторы линейно независимы:

Вычислим определитель, составленный из координат векторов :

, значит, векторы линейно независимы и образуют базис трехмерного пространства.

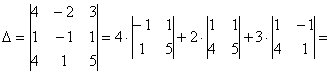
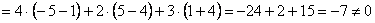
! Важно: координаты векторов обязательно записываем в столбцыопределителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.

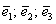
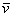
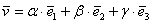
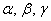
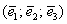
Теперь вспомним теоретическую часть: если векторы образуют базис, то любой вектор можно единственным способом разложить по данному базису: , где – координаты вектора в базисе .

Поскольку наши векторы образуют базис трёхмерного пространства (это уже доказано), то вектор можно единственным образом разложить по данному базису:
, где – координаты вектора в базисе .

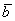
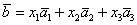
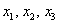
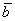
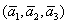
По условию и требуется найти координаты .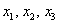

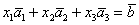
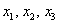
Для удобства объяснения поменяю части местами: . В целях нахождения следует расписать данное равенство покоординатно:

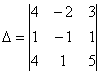
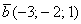
По какому принципу расставлены коэффициенты? Все коэффициенты левой части в точности перенесены из определителя , в правую часть записаны координаты вектора .

Получилась система трёх линейных уравнений с тремя неизвестными. Обычно её решают поформулам Крамера, часто даже в условии задачи есть такое требование.

Главный определитель системы уже найден:
, значит, система имеет единственное решение.

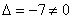
Дальнейшее – дело техники:

Таким образом:
– разложение вектора по базису .

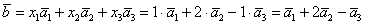
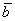
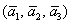
Ответ:

Как я уже отмечал, задача носит алгебраический характер. Векторы, которые были рассмотрены – это не обязательно те векторы, которые можно нарисовать в пространстве, а, в первую очередь, абстрактные векторы курса линейной алгебры. Для случая двумерных векторов можно сформулировать и решить аналогичную задачу, решение будет намного проще. Однако на практике мне такое задание ни разу не встречалось, именно поэтому я его пропустил в предыдущем разделе.

Такая же задача с трёхмерными векторами для самостоятельного решения:

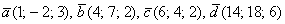
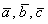
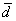
Даны векторы . Показать, что векторы образуют базис и найти координаты вектора в этом базисе. Систему линейных уравнений решить методом Крамера.

Полное решение и примерный образец чистового оформления в конце урока.

Аналогично можно рассмотреть четырёхмерное, пятимерное и т.д. векторные пространства, где у векторов соответственно 4, 5 и более координат. Для данных векторных пространств тоже существует понятие линейной зависимости, линейной независимости векторов, существует базис, в том числе, ортонормированный, разложение вектора по базису. Да, такие пространства невозможно нарисовать геометрически, но в них работают все правила, свойства и теоремы двух и трех мерных случаев – чистая алгебра. Собственно, о философских вопросах меня уже пробивало поговорить в статье Частные производные функции трёх переменных, которая появилась раньше данного урока.

Любите векторы, и векторы полюбят вас!

Решения и ответы:

Пример 2: Решение: составим пропорцию из соответствующих координат векторов:

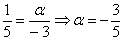
Ответ: при

Пример 4: Доказательство: Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
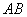
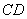
1) Проверим параллельность противоположных сторон и .
Найдём векторы:

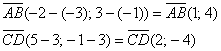
Вычислим определитель, составленный из координат векторов :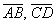
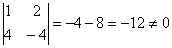
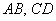
, значит, данные векторы не коллинеарны, и стороны не параллельны.
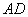
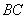
2) Проверим параллельность противоположных сторон и .
Найдём векторы:

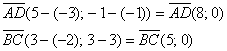
Вычислим определитель, составленный из координат векторов :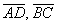
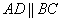
, значит, данные векторы коллинеарны, и .
Вывод: Две стороны четырёхугольника 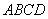параллельны, а две другие стороны не параллельны, значит, он является трапецией по определению. Что и требовалось доказать.

Пример 5: Решение:
б) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:

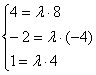
Система не имеет решения, значит, векторы 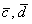не коллинеарны.
Более простое оформление:
– вторая и третья координаты не пропорциональны, значит, векторы не коллинеарны.
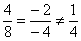
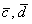
Ответ: векторы 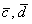не коллинеарны.
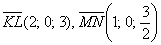
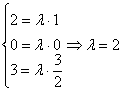
в) Исследуем на коллинеарность векторы . Составим систему:

Соответствующие координаты векторов пропорциональны, значит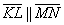
Вот здесь как раз не проходит «пижонский» метод оформления.
Ответ:

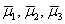
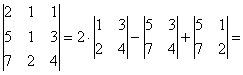
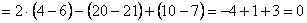
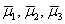
Пример 6: Решение: б) Вычислим определитель, составленный из координат векторов (определитель раскрыт по первой строке):

, значит, векторы линейно зависимы и не образуют базиса трёхмерного пространства.
Ответ: данные векторы не образуют базиса

Пример 9:Решение:Вычислим определитель, составленный из координат векторов :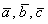

Таким образом, векторы 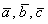линейно независимы и образуют базис.
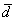
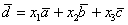
Представим вектор в виде линейной комбинации базисных векторов:

Покоординатно:

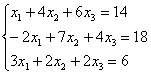
Систему решим по формулам Крамера:
, значит, система имеет единственное решение.

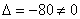
Ответ: Векторы 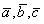образуют базис,

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Векторное произведение векторов.
Смешанное произведение векторов

На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов. Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов, требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение, даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)

Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урокаВекторы для чайников, чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах

Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы, а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!

Видео:Образуют ли данные векторы базисСкачать

Задача 40802 доказать,что векторы образуют базис.

Условие

доказать,что векторы образуют базис пространства

Решение

Стандартный базис в пространстве R^(3) имеет вид .
Чтобы доказать,что векторы a_(1);a_(2);a_(3) образуют базис, достаточно показать, что они линейно независимы.

Составляем их линейную комбинацию

[m]Delta =begin 2 & 2 &-1 \ 2 &-1 & 2\ -1 &2 & 2 end=-4-4-4+1-8-8neq 0[/m]

Система имеет единственное нулевое решение
α_(1)=α_(2)=α_(3)=0

Значит векторы линейно независимы и образуют базис

=(2 β β _(1)+2 β _(2)- β _(3))*x^2+(2 β _(1)- β _(2)+2 β _(3))*x+(- β _(1)+2 β _(2)+2 β _(3))

По условию
b=x^2+x+1

Решаем систему методом Крамера

[m]Delta =begin 2 & 2 &-1 \ 2 &-1 & 2\- 1 &2 & 2 end=-4-4-4+1-8-8=-27[/m]

[m]Delta_=begin 1 & 2 &-1 \ 1 &-1 & 2\ 1 &2 & 2 end=-2+4-2-1-4-4=-9[/m]

[m]Delta_ =begin 2 & 1 &-1 \ 2 &1 & 2\ -1 &1 & 2 end=4-2-2-1-4-4=-9[/m]

[m]Delta_ =begin 2 & 2 &1 \ 2 &-1 & 1\ -1 &2 & 1 end=-2-2+4-1-1-4=-9[/m]

💥 Видео

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Координаты в новом базисеСкачать

Решение, показать, что векторы а, b, с образуют базис, и найти координаты вектора d пример 8Скачать

Решение, показать, что векторы а, b, с образуют базис, и найти координаты вектора d пример 7Скачать

Решение, показать, что векторы а, b, с образуют базис, и найти координаты вектора d пример 6Скачать

Найдите разложение вектора по векторам (базису)Скачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

Решение, показать, что векторы а, b, с образуют базис, и найти координаты вектора d пример 4Скачать

Нахождение координат вектора. Практическая часть. 9 класс.Скачать

Семинар 3 - Задача 3 (Какие из векторов образуют базис?)Скачать

Решение, показать, что векторы e1, е2, е3 образуют базис и найти в нем координаты вектора а пример 3Скачать

Решение, показать, что векторы e1, е2, е3 образуют базис и найти в нем координаты вектора а пример 1Скачать

Решение, убедиться что векторы e1, е2, е3 образуют базис и найти в нем координаты вектора а пример 9Скачать

Координаты вектора в базисе. Собственные числа и векторы (решение задач)Скачать

Координаты вектора. 9 класс.Скачать

Базис. Разложение вектора по базису.Скачать

9 класс, 2 урок, Координаты вектораСкачать