Биссектрисы односторонних углов при параллельных прямых перпендикулярны

Видео:№ 211 - Геометрия 7-9 класс АтанасянСкачать

Докажите, что биссектрисы внутренних односторонних углов при двух параллельных прямых и секущей взаимно перпендикулярны

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Ваш ответ

Видео:№211. Две параллельные прямые пересечены секущей. Докажите, что: а) биссектрисыСкачать

решение вопроса

Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,658
• разное 16,822

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:ГЕОМЕТРИЯ 7 класс : Соответственные, односторонние и накрест лежащие углыСкачать

Биссектрисы односторонних углов при параллельных прямых перпендикулярны

§ 15. Свойства параллельных прямых

(обратная теореме 14.1)

Если две параллельные прямые пересечены секущей, то углы, образующие пару накрест лежащих углов, равны.

На рисунке 224 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 = ∠ 2.

Пусть ∠ 1 ≠ ∠ 2. Тогда через точку K проведём прямую a 1 так, чтобы ∠ 3 = ∠ 2 (рис. 224). Углы 3 и 2 являются накрест лежащими при прямых a 1 и b и секущей c . Тогда по теореме 14.1 a 1 ‖ b . Получили, что через точку K проходят две прямые, параллельные прямой b . Это противоречит аксиоме параллельности прямых. Таким образом, наше предположение неверно, и, следовательно, ∠ 1 = ∠ 2.

(обратная теореме 14.3)

Если две параллельные прямые пересечены секущей, то углы, образующие пару соответственных углов, равны.

На рисунке 225 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 = ∠ 2.

По теореме 15.1 углы 3 и 2 равны как накрест лежащие при параллельных прямых a и b и секущей c . Но углы 3 и 1 равны как вертикальные. Следовательно, ∠ 1 = ∠ 2.

(обратная теореме 14.2)

Если две параллельные прямые пересечены секущей, то сумма углов, образующих пару односторонних углов, равна 180° .

На рисунке 226 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 + ∠ 2 = 180°.

По теореме 15.1 углы 3 и 2 равны как накрест лежащие при параллельных прямых a и b и секущей c . Но углы 3 и 1 смежные, поэтому ∠ 1 + ∠ 3 = 180°. Следовательно, ∠ 1 + ∠ 2 = 180°.

Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой ( рис. 227 ).

Докажите это следствие самостоятельно.

Задача. Докажите, что все точки одной из двух параллельных прямых равноудалены от другой прямой.

Решение. Пусть прямые a и b параллельны (рис. 228), M и N — две произвольные точки прямой a . Опустим из них перпендикуляры MK и NP на прямую b . Докажем, что MK = NP .

Рассмотрим треугольники MKN и PNK . Отрезок KN — их общая сторона. Так как MK ⊥ b и NP ⊥ b , то MK ‖ NP , а углы MKN и PNK равны как накрест лежащие при параллельных прямых MK и NP и секущей KN .

Аналогично углы MNK и PKN равны как накрест лежащие при параллельных прямых MN и KP и секущей KN . Следовательно, треугольники MKN и PNK равны по стороне и двум прилежащим углам.

Тогда MK = NP .

Расстоянием между двумя параллельными прямыми называют расстояние от любой точки одной из прямых до другой прямой.

Например, на рисунке 228 длина отрезка MK — это расстояние между параллельными прямыми a и b .

Задача. На рисунке 229 отрезок AK — биссектриса треугольника ABC , MK ‖ AC . Докажите, что треугольник AMK — равнобедренный.

Решение. Так как AK — биссектриса треугольника ABC , то ∠ MAK = ∠ KAC .

Углы KAC и MKA равны как накрест лежащие при параллельных прямых MK и AC и секущей AK . Следовательно, ∠ MAK = ∠ MKA .

Тогда треугольник AMK — равнобедренный.

1. Каким свойством обладают накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей?
2. Каким свойством обладают соответственные углы, образованные при пересечении двух параллельных прямых секущей?
3. Чему равна сумма односторонних углов, образованных при пересечении двух параллельных прямых секущей?
4. Известно, что прямая перпендикулярна одной из двух параллельных прямых. Обязательно ли она перпендикулярна другой прямой?
5. Что называют расстоянием между двумя параллельными прямыми?

326. На рисунке 230 найдите угол 1.

327. На рисунке 231 найдите угол 2.

328. Разность односторонних углов, образованных при пересечении двух параллельных прямых секущей, равна 50°. Найдите эти углы.

329. Один из односторонних углов, образованных при пересечении двух параллельных прямых секущей, в 4 раза больше другого. Найдите эти углы.

330. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если:

1) один из этих углов равен 48°;

2) отношение градусных мер двух из этих углов равно 2 : 7.

331. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них на 24° меньше другого.

332. На рисунке 232 m ‖ n , p ‖ k , ∠1 = 50°. Найдите ∠ 2, ∠ 3 и ∠ 4.

333. Прямая, параллельная основанию AC равнобедренного треугольника ABC , пересекает его боковые стороны AB и BC в точках D и F соответственно. Докажите, что треугольник DBF — равнобедренный.

334. На продолжениях сторон AC и BC треугольника ABC ( AB = BC ) за точки A и B отметили соответственно точки P и K так, что PK ‖ AB . Докажите, что треугольник KPC — равнобедренный.

335. Отрезки AB и CD пересекаются в точке O , AO = BO , AC ‖ BD . Докажите, что CO = DO .

336. Отрезки MK и DE пересекаются в точке F , DK ‖ ME , DK = ME . Докажите, что ∆ MEF = ∆ DKF .

337. Ответьте на вопросы.

1) Могут ли оба односторонних угла при двух параллельных прямых и секущей быть тупыми?

2) Может ли сумма накрест лежащих углов при двух параллельных прямых и секущей быть равной 180°?

3) Могут ли быть равными односторонние углы при двух параллельных прямых и секущей?

338. На рисунке 233 AB ‖ CD , BC ‖ AD . Докажите, что BC = AD .

339. На рисунке 233 BC = AD , BC ‖ AD . Докажите, что AB ‖ CD .

340. На рисунке 234 MK ‖ EF , ME = EF , ∠ KMF = 70°. Найдите ∠ MEF .

341. Через вершину B треугольника ABC (рис. 235) провели прямую MK , параллельную прямой AC , ∠ MBA = 42°, ∠ CBK = 56°. Найдите углы треугольника ABC .

342. Прямая, проведённая через вершину A треугольника ABC параллельно его противолежащей стороне, образует со стороной AC угол, равный углу BAC . Докажите, что данный треугольник — равнобедренный.

343. На рисунке 236 ∠ MAB = 50°, ∠ ABK = 130°, ∠ ACB = 40°, CE — биссектриса угла ACD . Найдите углы треугольника ACE .

344. На рисунке 237 BE ⊥ AK , CF ⊥ AK , CK — биссектриса угла FCD , ∠ ABE = 32°. Найдите ∠ ACK .

345. На рисунке 238 BC ‖ MK , BK = KE , CK = KD . Докажите, что AD ‖ MK .

346. На рисунке 239 AB = AC , AF = FE , AB ‖ EF . Докажите, что AE ⊥ BC .

347. Треугольник ABC — равнобедренный с основанием AC . Через произвольную точку M его биссектрисы BD проведены прямые, параллельные его сторонам AB и BC и пересекающие отрезок AC в точках E и F соответственно. Докажите, что DE = DF .

348. На рисунке 240 AB ‖ DE . Докажите, что ∠ BCD = ∠ ABC + ∠ CDE .

349. На рисунке 241 AB ‖ DE , ∠ ABC = 120°, ∠ CDE = 150°. Докажите, что BC ⊥ CD .

350. Через вершину B треугольника ABC провели прямую, параллельную его биссектрисе AM . Эта прямая пересекает прямую AC в точке K . Докажите, что ∆ BAK — равнобедренный.

351. Через точку O пересечения биссектрис AE и CF треугольника ABC провели прямую, параллельную прямой AC . Эта прямая пересекает сторону AB в точке M , а сторону BC — в точке K . Докажите, что MK = AM + CK .

352. Биссектрисы углов BAC и BCA треугольника ABC пересекаются в точке O . Через эту точку проведены прямые, параллельные прямым AB и BC и пересекающие сторону AC в точках M и K соответственно. Докажите, что периметр треугольника MOK равен длине стороны AC .

Упражнения для повторения

353. На отрезке AB отметили точку C так, что AC : BC = 2 : 1. На отрезке AC отметили точку D так, что AD : CD = 3 : 2. В каком отношении точка D делит отрезок AB ?

354. Отрезки AC и BD пересекаются в точке O , AB = BC = CD = AD . Докажите, что AC ⊥ BD .

355. В треугольнике MOE на стороне MO отметили точку A , в треугольнике TPK на стороне TP — точку B так, что MA = TB . Какова градусная мера угла BKP , если MO = TP , ∠ M = ∠ T , ∠ O = ∠ P , ∠ AEO = 17°?

Наблюдайте, рисуйте, конструируйте, фантазируйте

356. На рисунке 242 изображена очень сложная замкнутая ломаная. Она ограничивает некоторую часть плоскости (многоугольник). Как, отметив на рисунке любую точку, по возможности быстрее определить, принадлежит эта точка многоугольнику или нет?

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Признаки параллельности прямых

При пересечении двух прямых третьей прямой образуются углы, названия которых приведены в следующей таблице.

Видео:№208. Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50°Скачать

Углы, образующиеся при пересечении двух прямых третьей прямой

Рисунок	Определение углов
	Внутренние накрест лежащие углы
	Внешние накрест лежащие углы
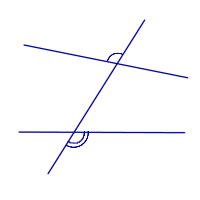	Соответственные углы
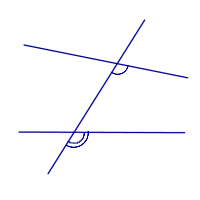	Внутренние односторонние углы
	Внешние односторонние углы

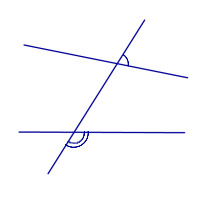Внутренние накрест лежащие углы

Внешние накрест лежащие углы

Соответственные углы

Внутренние односторонние углы

Внешние односторонние углы

Перечисленные в таблице углы используются в формулировках признаков параллельности двух прямых.

Определение . Две прямые на плоскости называются параллельными, если они не имеют общих точек.

Замечание . Два отрезка называются параллельными , если они лежат на параллельных прямых.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Признаки параллельности двух прямых

Рисунок	Признак параллельности
	Прямые параллельны тогда и только тогда, когда внутренние накрест лежащие углы равны
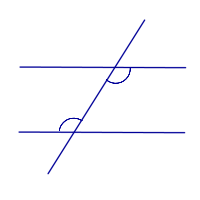	Прямые параллельны тогда и только тогда, когда внешние накрест лежащие углы равны
	Прямые параллельны тогда и только тогда, когда соответственные углы равны
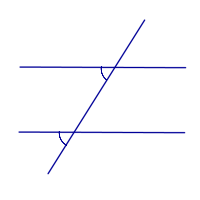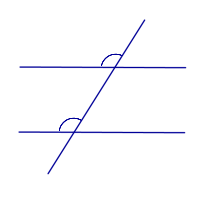	Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180°
	Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180°

Прямые параллельны тогда и только тогда,
когда внутренние накрест лежащие углы равны

Прямые параллельны тогда и только тогда,
когда внешние накрест лежащие углы равны

Прямые параллельны тогда и только тогда,
когда соответственные углы равны

Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180°

Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180°

Рисунок	Признак параллельности
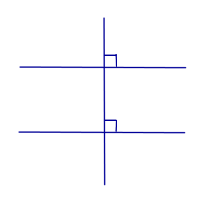	Две прямые, перпендикулярные к третьей прямой, параллельны

Две прямые, перпендикулярные к третьей прямой, параллельны

Переход свойства параллельности прямых

Рисунок	Признак параллельности
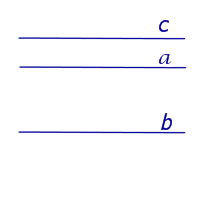	Если прямая a параллельна прямой b , а прямая b параллельна прямой c , то прямая a параллельна прямой c

Если прямая a параллельна прямой b ,
а прямая b параллельна прямой c ,
то прямая a параллельна прямой c

Задача . Доказать, что биссектрисы внутренних односторонних углов, полученных при пересечении двух параллельных прямых третьей прямой, перпендикулярны.

Решение . Решение этой задачи почти дословно совпадает с решением задачи из раздела нашего справочника «Углы на плоскости» и предоставляется читателю в качестве несложного самостоятельного упражнения.

📺 Видео

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

УГЛЫ ПРИ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ И СЕКУЩЕЙСкачать

Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

ГЕОМЕТРИЯ 7 класс. Признаки параллельности, накрест лежащие, соответственные и односторонние углыСкачать

УГЛЫ: Односторонние, Накрест Лежащие, Внутренние, Внешние // Теорема об углах — Геометрия 7 классСкачать

№1,17 | Все теория по планиметрии за 4 часа | Решаем все прототипы №1 из ФИПИСкачать

Геометрия № 83 №211 Задача найти угол между биссектрисами смежных и односторонних угловСкачать

Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать

Теорема 14.1 Если накрест лежащие углы равны, то прямые параллельныСкачать

7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Параллельные прямые (задачи).Скачать

Биссектриса угла параллелограмма ▶ (Мини-ликбез №5)Скачать