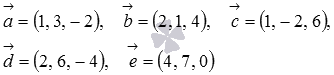Доказать что точки лежат в одной плоскости через векторы

В этой статье мы поговорим о компланарности векторов. Сначала вспомним определение компланарности и получим необходимое и достаточное условие компланарности трех векторов в трехмерном пространстве. Далее разберемся с задачей исследования системы из n векторов на компланарность, рассмотрим решения характерных примеров.

Навигация по странице.

Видео:Доказать, что точки лежат в одной плоскости - bezbotvyСкачать

Необходимое и достаточное условие компланарности трех векторов.

Напомним определение компланарных векторов.

Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.

Два вектора и трехмерного пространства всегда компланарны. Это утверждение легко доказать. Пусть a и b – прямые, на которых лежат векторы и соответственно. Проведем через начало вектора прямую b₁ , параллельную прямой b , а через начало вектора прямую a₁ , праллельную прямой a . Плоскости, образуемые прямыми a и b₁ , а так же прямыми b и a₁ , параллельны по построению, а векторы и принадлежат им. Следовательно, векторы и компланарны.

А как же определить, являются ли три вектора компланарными?

Для этого существует необходимое и достаточное условие компланарности трех векторов в пространстве. Оно основано на понятии смешанного произведения векторов. Сформулируем его в виде теоремы.

Для компланарности трех векторов и трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

Пусть , докажем что векторы и компланарны.

Так как , то векторы и перпендикулярны в силу необходимого и достаточного условия перпендикулярности двух векторов. С другой стороны, по определению векторного произведения вектор перпендикулярен и вектору и вектору . Следовательно, векторы и компланарны, так как перпендикулярны одному вектору .

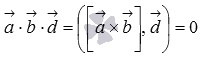
Пусть теперь векторы и компланарны, докажем равенство нулю смешанного произведения .

Так как векторы и компланарны, то вектор перпендикулярен каждому из них, следовательно, скалярное произведение вектора на равно нулю, что означает равенство нулю смешанного произведения .

Итак, теорема полностью доказана.

Покажем применение доказанного условия компланарности трех векторов к решению задач.

Компланарны ли векторы , заданные в прямоугольной системе координат.

Вычислим их смешанное произведение по координатам:

Так как мы получили ноль, то условие компланарности выполнено, следовательно, заданные векторы компланарны.

Необходимое и достаточное условие компланарности векторов можно использовать для проверки принадлежности четырех точек пространства А, В, С и D одной плоскости. Для этого находим координаты векторов и вычисляем их смешанное произведение. Если оно равно нулю, то точки лежат в одной плоскости, в противном случае – не лежат в одной плоскости.

Принадлежат ли точки 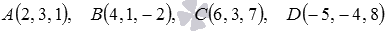одной плоскости?

Найдем координаты векторов (при необходимости смотрите статью нахождение координат вектора по координатам точек его начала и конца):

Теперь вычисляем смешанное произведение этих векторов

Так как смешанное произведение векторов отлично от нуля, то векторы не компланарны, следовательно, точки А, В, С и D не лежат в одной плоскости.

Видео:Как проверить лежат ли 4 точки в одной плоскости Аналитическая геометрияСкачать

Исследование системы векторов на компланарность, примеры и решения.

А как же быть, если требуется установить компланарность системы векторов, число векторов которой больше трех?

Давайте ответим на этот вопрос и получим условие компланарности системы из n векторов трехмерного пространства.

В предыдущем пункте мы показали, что для компланарности трех векторов и необходимо и достаточно равенство нулю их смешанного произведения: . Так как смешанное произведение трех векторов в координатной форме представляет собой определитель матрицы, строками которой являются координаты векторов и , то условие компланарности можно записать в виде . Вспомнив понятие ранга матрицы, последнее равенство можно интерпретировать следующим образом: ранг матрицы, строками которой являются координаты компланарных векторов и , меньше трех.

Обобщив последнее утверждение, мы получим необходимое и достаточное условие компланарности системы из n векторов трехмерного пространства: для компланарности системы из n векторов трехмерного пространства необходимо и достаточно, чтобы ранг матрицы, строками которой являются координаты векторов системы, был меньше трех.

Компланарны ли векторы

Составим матрицу, строками которой примем координаты данных векторов

Сразу легко отыскать минор второго порядка, отличный от нуля, .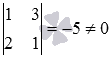

Переберем окаймляющие его миноры третьего порядка:

Все они равны нулю, следовательно, ранг матрицы равен двум, поэтому, векторы заданной системы векторов компланарны в силу выполнения необходимого и достаточного условия компланарности.

Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Общее уравнение плоскости : описание, примеры, решение задач

В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.

Видео:Координаты точки и координаты вектора 1.Скачать

Общее уравнение плоскости: основные сведения

Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.

Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.

Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.

Теорема состоит из двух частей. Разберем доказательство каждой из них.

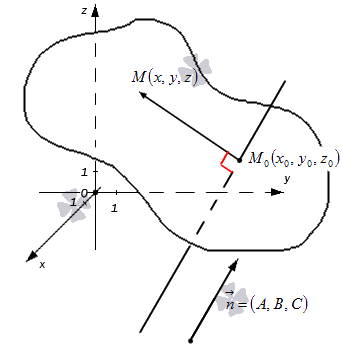
1. Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .

Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:

n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )

Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.

1. Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.

В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.

Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.

Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.

Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.

Раскроем чуть шире смысл теорем.

В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.

Укажем пример как иллюстрацию этих утверждений.

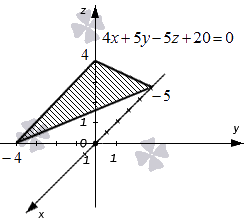
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.

Видео:№4. Точки А, В, С и D не лежат в одной плоскости, а) Могут ли какие-то три изСкачать

Общее уравнение плоскости, проходящей через точку

Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.

Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0

Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.

Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:

2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0

Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.

В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение

Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:

λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.

Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0

Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .

Возможно получить это уравнение другим способом.

Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.

Решение

Рассмотрим два способа решения.

1. Исходные условия позволяют получить следующие данные:

x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5

Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0

1. Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:

M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0

Ответ: 3 x + 7 y — 5 z — 26 = 0

Видео:№12. Точки А, В, С, D не лежат в одной плоскости. Пересекаются ли плоскости, проходящие через точкиСкачать

Неполное общее уравнение плоскости

Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

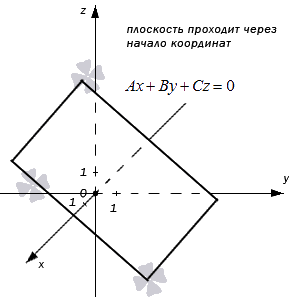
1. В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0

Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:

A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

1. Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.

1. При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.

Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0

Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.

Р​​ешение

У​​​​​словием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .

Задачу возможно решить еще одним способом.

Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0

Ответ: x — 7 = 0

Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .

Решение

Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .

Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .

Видео:10 класс, 3 урок, Некоторые следствия из аксиомСкачать

РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ АФФИННОЙ ГЕОМЕТРИИ ВЕКТОРНЫМ МЕТОДОМ

Видео:Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

ЗАДАЧИ, СВЯЗАННЫЕ С ДОКАЗАТЕЛЬСТВОМ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ И ОТРЕЗКОВ, ПРЯМЫХ И ПЛОСКОСТЕЙ

При решении этих задач наиболее часто используется признак коллинеарности двух векторов (соотношение 1) и единственность разложения вектора по двум неколлинеарным векторам (соотношение 7).

Задача 1. Доказать что вектор, концами которого являются середины двух противолежащих сторон, равен половине векторной суммы двух других противолежащих (соотношение 8)

Решение. Пусть О — произвольная точка. Согласно соотношению 3 имеем

Задача 2. Доказать, что отрезок, соединяющий середины диагоналей трапеции, параллелен ее основаниям.

AC, ВD — диагонали

Доказать: MN || AD.

Анализ. Покажем, что MN || AD. Для этого достаточно показать, что коллинеарен

Решение. Так как M и N — середины отрезков AC и BD, то(соотношение 3)

Но коллинеарен вектору , поэтому Тогда

Тогда (по соотношению 1) коллинеарен что и требовалось доказать.

Задача 3. Доказать, что средняя линия трапеции параллельна основаниям и длина ее равна полусумме длин оснований.

Анализ. Для доказательства параллельности достаточно показать, что векторы и коллинеарны

1) Согласно рассмотренной задаче 1 .

2) Так как , то и, значит, MN || AD.

3) Так как , то = AD + BC, поэтому

Задача 4. Точки K, L, M, N — середины сторон AB, BC, CD, DE пятиугольника ABCDE, а точки P и Q — середины отрезков KM и LN. Докажите, что PQ || AE и PQ = 1/4 AE.

K, L, M, N — середины сторон AB, BC, CD, DE

P и Q — середины отрезков KM и LN

Доказать PQ || AE и PQ = 1/4 AE.

Пусть О — произвольная точка. Согласно соотношению 3

Из этих равенств следует, что

Отсюда следует, что PQ || AE и PQ = AE.

Задача 5. В параллелепипеде АВСDА₁В₁С₁D₁ точка М?— середина диагонали А₁С₁ грани A₁B₁C₁D₁, точка K— середина ребра ВВ₁. Докажите, что прямые А₁В₁, KМ и ВС₁ параллельны некоторой плоскости.

K— середина ребра ВВ₁

Решение. Введем векторы

Тройку некомпланарных векторов примем в качестве базиса. Разложим векторы по векторам этого базиса.

Это означает, что векторы компланарны, следовательно, они параллельны некоторой плоскости , тогда этой плоскости параллельны и прямые А₁В₁, KМ и ВС₁, для которых векторы являются направляющими.

Практика решения более сложных задач такого типа показала, что работу нужно вести в следующем направлении: постараться разложить один из векторов (чаще всего конец такого вектора — точка, которая делит данный отрезок в заданном отношении) по двум основным векторам (они неколлинеарны) двумя различными способами. Используя единственность разложения вектора по двум неколлинеарным векторам, установить зависимость между коэффициентами в разложении вектора, что потом дает возможность найти искомое соотношение.

Задача 7. На стороне AC треугольника ABC взята точка M так, что , а на продолжении стороны BC такая точка N что . В каком отношении точка P пересечения AB и MN делит каждый из этих отрезков.

Выберем базисные векторы

Разложим вектор по базисным двумя различными способами

а) =y, тогда =, т.к. векторы сонаправлены

Учитывая единственность разложения вектора по двум неколлинеарным векторам(соотношение 7) , получим систему

Задача 8. Отрезок, соединяющий вершину тетраэдра с центроидом противолежащей грани, называется медианой этого тетраэдра. Докажите что все медианы тетраэдра пересекаются в одной точке и эта точка делит каждую из медиан в отношении 3:1, считая от вершины.

Пусть Н₁, Н₂, Н₃, Н₄ — центроиды граней соответственно АВС, АВР, ВСР, АСР; М — точка, делящая медиану РН₁ тетраэдра РАВС в отношении РМ:МН₁ = 3:1.

Тогда РМ : РН₁ = 3 : 4, откуда Для любой точки О пространства и центроида Н₁ грани АВС выполняется:

Аналогично доказывается, что для точек М₁, М₂ и М₃, делящих медианы соответственно СН₂, АН₃, ВН₄ тетраэдра в отношении 3 : 1, считая соответственно от вершин С, А и В, выполняется то же равенство, то есть

Это означает, что точки М, М₁, М₂ и М₃ совпадают, то есть все четыре медианы РН₁, СН₂, АН₃ и ВН₄ тетраэдра пересекаются в одной точке М и делятся этой точкой в отношении 3:1, считая от соответствующей вершины, что и требовалось доказать.

Задача 9. На диагоналях АВ₁ и ВС₁ граней AA₁B₁B и ВВ₁С₁С параллелепипеда ABCDA₁B₁C₁D₁ взяты точки соответственно Н и M так, что отрезки MН и A₁C параллельны. Найдите отношение длин этих отрезков.

Тройку некомпланарных векторов примем в качестве базиса и разложим векторы по векторам этого базиса.

Так как точка Н лежит на диагонали АВ₁, то векторы коллинеарны, поэтому (соотношение 7) существует такое число х, что Аналогично, в силу коллинеарности векторов существует такое число у, что

По правилу ломаной находим:

По условию MН A₁C, значит, существует такое число t, что то есть выполняется равенство:

Вследствие некомпланарности векторов и единственности разложения вектора по базису, приходим к выводу: 1- х-t =0, t-у=0, х-у-t = 0. Решением этой системы уравнений является: Тогда значит, МН:СА₁ = 1 : 3.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

ЗАДАЧИ НА ДОКАЗАТЕЛЬСТВО ИЛИ ИСПОЛЬЗОВАНИЕ ПРИНАДЛЕЖНОСТИ ТРЁХ ТОЧЕК ПРЯМОЙ

Задача 10. Точки M и N лежат соответственно на сторонах AD и BC четырехугольника ABCD, причем AM:MD=BN:NC== 3:4.

Докажите, что середины отрезков AB, MN и CD лежат на одной прямой.

Доказательство. Пусть K₁ — середина AB, K₂ — середина MN, K₃ — середина CD. Согласно соотношению 8 имеем

Из условия следует, что ,

Таким образом, векторы и коллинеарны, и, значит, точки K₁, K₂ и K₃ лежат на одной прямой.

🎬 Видео

№6. Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.Скачать

№3. Верно ли, что: а) любые три точки лежат в одной плоскости;Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Задачка из советского учебника. Докажите, что точки А, С и Е лежат на одной прямойСкачать

№5. Докажите, что через три данные точки, лежащие на прямой, проходит плоскость.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Координаты вектора. 9 класс.Скачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

№15. Три прямые попарно пересекаются. Докажите, что они либо лежат в одной плоскостиСкачать

Векторы в координатной плоскости.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать