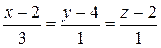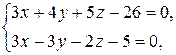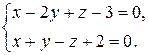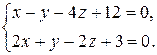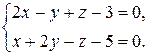Доказать что прямая x 3t 2 y 4t 1 z 4t 5 параллельна плоскости (3 видео)

Прямая и плоскость

Дата добавления: 2015-08-06 ; просмотров: 3999 ; Нарушение авторских прав

149.Найти угол прямой y = 3x – 1 , 2z = – 3x + 2 с плоскостью

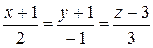
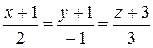
150.Показать, что прямая параллельна плоскости 2x + y – z = 0, а прямая лежит в этой плоскости.

151.Написать уравнение плоскости, проходящей через точку (–1, 2, –3), перпендикулярно к прямой x = 2, y – z = 1.

152.Написать уравнение плоскости, проходящей через прямую

и точку (3, 4, 0).

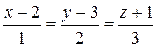
153.Написать уравнение плоскости, проходящей через прямую

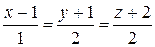
перпендикулярно к плоскости 2x + 3y – z = 4.

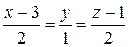
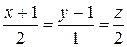
154.Написать уравнение плоскости, проходящей через параллельные прямые и .

155.Написать уравнение прямой, проходящей через начало координат и составляющей равные углы с плоскостями 4y = 3x, y = 0 и z = 0. Найти эти углы.

156.Найти точку пересечения прямой x = 2t – 1, y = t + 2, z = 1 – t с плоскостью 3x – 2y + z = 3.

157.Найти точку пересечения прямой 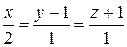с плоскостью x + 2y + 3z – 29 = 0.

158.Найти проекцию точки (3, 1, – 1) на плоскость x + 2y + 3z – 30 =0.

159.Найти проекцию точки (2, 3, 4) на прямую x = y = z.

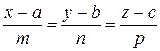
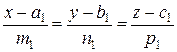
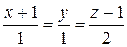
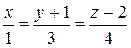
160.Найти кратчайшее расстояние d между непараллельными прямыми: и ; и ;

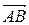
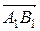
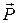
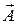
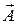
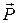
Указание.Предполагая прямые в общем случае скрещивающимися, нарисуем параллельные плоскости, в которых они расположены. Из точек А(a, b, c) и А₁(a₁, b₁, c₁)проведем векторы = = <m; n; p> и = ₁ = ₁ <m₁; n₁; p₁>. Высота призмы ABCA₁B₁C₁ и равна искомому расстоянию.

161.Показать, что прямые x = z – 2, y = 2z + 1 и

пересекаются, и написать уравнение плоскости, в которой они расположены.

162.Написать уравнение перпендикуляра, опущенного из точки (2, 1, 0) на прямую x = 3z – 1, y = 2z.

163.Построить плоскость x + y – z = 0 и прямую, проходящую через точки A(0, 0, 4) и B(2, 2, 0). Найти точку пересечения прямой с плоскостью и угол между ними.

164.Построить плоскость y = z, прямую x = – z + 1, y = 2 и найти: 1) точку их пересечения; 2) угол между ними.

165.Найти проекцию точки (3, 1, – 1) на плоскость 3x + y + z – 20 = 0.

166.Найти проекцию точки (1, 2, 8) на прямую .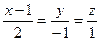

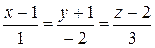
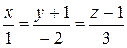
167.Написать уравнение плоскости, проходящей через параллельные прямые и .

168.Показать, что прямые 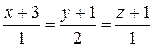и x = 3z – 4, y = z + 2 пересекаются, найти точку их пересечения.

169.Написать уравнения перпендикуляра, опущенного из точки (1, 0, – 1) на прямую .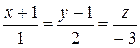

170.Найти кратчайшее расстояние между прямыми x = – 2y = z и x = y = 2.

171.Доказать, что прямая x = 3t – 2, y = – 4t + 1, z = 4t – 5 параллельна плоскости 4x – 3y – 6z – 5 = 0.

172.Доказать, что прямая 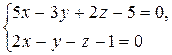лежит в плоскости

173.Найти точку пересечения прямой и плоскости:

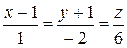
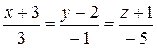
1) , 2x + 3y + z – 1 = 0;

2) , x – 2y + z – 15 = 0;

3) , x + 2y – 2z + 6 = 0.

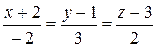
174.Составить каноническое уравнение прямой, проходящей через точку M₀(2, – 4, – 1) и середину отрезка прямой

заключенного между плоскостями 5x + 3y – 4z + 11 = 0, 5x + 3y – 4z – 41 = 0.

175.Составить уравнения прямой, проходящей через точку M₀ (2, – 3, –5) перпендикулярно к плоскости 6x – 3y – 5z + 2 = 0.

176.Составить уравнение плоскости, проходящей через точку M₀ (1, –1, –1) перпендикулярно к прямой .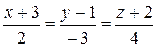

177.Составить уравнение плоскости, проходящей через точку M₀ (1, – 2, 1) перпендикулярно к прямой

178.При каких значениях A и D прямая x = 3 + 4t, y = 1 – 4t, z = – 3 + t лежит в плоскости A x + 2y – 4z + D = 0 ?

179.При каких значениях A и B плоскость A x + By + 3z – 5 = 0 перпендикулярна к прямой x = 3 + 2t, y = 5 – 3t, z = – 2 – 2t ?

180.При каких значениях l C прямая 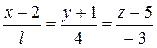перпендикулярна к плоскости 3x – 2y + Cz + 1 = 0 ?

181.Найти проекцию точки P(2, –1, 3) на прямую x = 3t, y = 5t – 7, z = 2t + 2.

182.Найти точку Q, симметричную точке P(4, 1, 6) относительно прямой

183.Найти точку Q, симметричную точке P(2, –5, 7) относительно прямой, проходящей через точки M₁(5, 4, 6) и M₂(–2, –17, -8).

184.Найти проекцию точки P(5, 2, –1) на плоскость 2x – y + 3z + 23 = 0.

185.Найти точку Q, симметричную точке P(1, 3, – 4) относительно плоскости 3x + y – 2z = 0.

186.Составить уравнение плоскости, проходящей через две параллельные прямые , .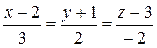

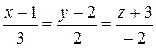
187.Найти проекцию точки C(3, –4, –2) на плоскость, проходящую через параллельные прямые , .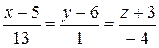

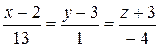
188.Составить уравнение плоскости, проходящей через прямую x = 3t + 1, y = 2t + 3, z = – t – 2 параллельно прямой

189.Составить уравнение плоскости, проходящей через прямую

перпендикулярно к плоскости 3x + 2y – z – 5 = 0.

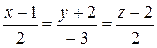
190.Составить каноническое уравнение прямой, которая проходит через точку M₀(3, –2, –4) параллельно плоскости 3x – 2y – 3z – 7 = 0 и пересекает прямую .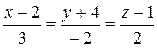

191.Составить параметрические уравнения прямой, которая проходит параллельно плоскостям 3x + 12y – 3z – 5 = 0, 3x – 4y + 9z + 7 = 0 и пересекает прямые , .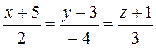

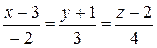
192.Вычислить кратчайшее расстояние между двумя прямыми в каждом из следующих случаев:

1) ; ;

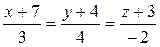
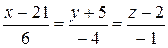
3) ; x = 6t + 9, y = – 2t, z = – t + 2.

Содержание

Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости
Параллельные прямые и плоскость – основные сведения
Параллельность прямой и плоскости – признак и условия параллельности
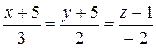
Доказать что прямая x 3t 2 y 4t 1 z 4t 5 параллельна плоскости
📽️ Видео

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Параллельные прямая и плоскость, признак и условия параллельности прямой и плоскости

Статья рассматривает понятия параллельность прямой и плоскости. Будут рассмотрены основные определения и приведены примеры. Рассмотрим признак параллельности прямой к плоскости с необходимыми и достаточными условиями параллельности, подробно решим примеры заданий.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Параллельные прямые и плоскость – основные сведения

Прямая и плоскость называются параллельными, если не имеют общих точек, то есть не пересекаются.

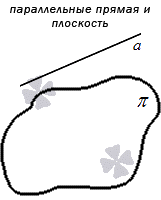
Параллельность обозначается « ∥ ». Если в задании по условию прямая a и плоскость α параллельны, тогда обозначение имеет вид a ∥ α . Рассмотрим рисунок, приведенный ниже.

Считается, что прямая a , параллельная плоскости α и плоскость α , параллельная прямой a , равнозначные, то есть прямая и плоскость параллельны друг другу в любом случае.

Видео:Параллельность прямой к плоскостиСкачать

Параллельность прямой и плоскости – признак и условия параллельности

Не всегда очевидно, что прямая и плоскость параллельны. Зачастую это нужно доказать. Необходимо использовать достаточное условие, которое даст гарантию на параллельность. Такой признак имеет название признака параллельности прямой и плоскости. Предварительно рекомендуется изучить определение параллельных прямых.

Если заданная прямая a , не лежащая в плоскости α , параллельна прямой b , которая принадлежит плоскости α , тогда прямая a параллельна плоскости α .

Рассмотрим теорему, используемую для установки параллельности прямой с плоскостью.

Если одна из двух параллельных прямых параллельна плоскости, то другая прямая лежит в этой плоскости либо параллельна ей.

Подробное доказательство рассмотрено в учебнике 10 — 11 класса по геометрии. Необходимым и достаточным условием параллельности прямой с плоскостью возможно при наличии определения направляющего вектора прямой и нормального вектора плоскости.

Для параллельности прямой a , не принадлежащей плоскости α , и данной плоскости необходимым и достаточным условием является перпендикулярность направляющего вектора прямой с нормальным вектором заданной плоскости.

Условие применимо, когда необходимо доказать параллельность в прямоугольной системе координат трехмерного пространства. Рассмотрим подробное доказательство.

Допустим, прямая а в систему координат О х у задается каноническими уравнениями прямой в пространстве , которые имеют вид x — x 1 a x = y — y 1 a y = z — z 1 a z или параметрическими уравнениями прямой в пространстве x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , плоскостью α с общими уравнениями плоскости A x + B y + C z + D = 0 .

Отсюда a → = ( a x , a y , a z ) является направляющим вектором с координатами прямой а, n → = ( A , B , C ) — нормальным вектором заданной плоскости альфа.

Чтобы доказать перпендикулярность n → = ( A , B , C ) и a → = ( a x , a y , a z ) , нужно использовать понятие скалярного произведения. То есть при произведении a → , n → = a x · A + a y · B + a z · C результат должен быть равен нулю из условия перпендикулярности векторов.

Значит, что необходимым и достаточным условием параллельности прямой и плоскости запишется так a → , n → = a x · A + a y · B + a z · C . Отсюда a → = ( a x , a y , a z ) является направляющим вектором прямой a с координатами, а n → = ( A , B , C ) — нормальным вектором плоскости α .

Определить, параллельны ли прямая x = 1 + 2 · λ y = — 2 + 3 · λ z = 2 — 4 · λ с плоскостью x + 6 y + 5 z + 4 = 0 .

Получаем, что предоставленная прямая не принадлежит плоскости, так как координаты прямой M ( 1 , — 2 , 2 ) не подходят. При подстановке получаем, что 1 + 6 · ( — 2 ) + 5 · 2 + 4 = 0 ⇔ 3 = 0 .

Необходимо проверить на выполнимость необходимое и достаточное условие параллельности прямой и плоскости. Получим, что координаты направляющего вектора прямой x = 1 + 2 · λ y = — 2 + 3 · λ z = 2 — 4 · λ имеют значения a → = ( 2 , 3 , — 4 ) .

Нормальным вектором для плоскости x + 6 y + 5 z + 4 = 0 считается n → = ( 1 , 6 , 5 ) . Перейдем к вычислению скалярного произведения векторов a → и n → . Получим, что a → , n → = 2 · 1 + 3 · 6 + ( — 4 ) · 5 = 0 .

Значит, перпендикулярность векторов a → и n → очевидна. Отсюда следует, что прямая с плоскостью являются параллельными.

Ответ: прямая с плоскостью параллельны.

Определить параллельность прямой А В в координатной плоскости О у z , когда даны координаты A ( 2 , 3 , 0 ) , B ( 4 , — 1 , — 7 ) .

По условию видно, что точка A ( 2 , 3 , 0 ) не лежит на оси О х , так как значение x не равно 0 .

Для плоскости O x z вектор с координатами i → = ( 1 , 0 , 0 ) считается нормальным вектором данной плоскости. Обозначим направляющий вектор прямой A B как A B → . Теперь при помощи координат начала и конца рассчитаем координаты вектора A B . Получим, что A B → = ( 2 , — 4 , — 7 ) . Необходимо выполнить проверку на выполнимость необходимого и достаточного условия векторов A B → = ( 2 , — 4 , — 7 ) и i → = ( 1 , 0 , 0 ) , чтобы определить их перпендикулярность.

Запишем A B → , i → = 2 · 1 + ( — 4 ) · 0 + ( — 7 ) · 0 = 2 ≠ 0 .

Отсюда следует, что прямая А В с координатной плоскостью О y z не являются параллельными.

Ответ: не параллельны.

Не всегда заданное условие способствует легкому определению доказательства параллельности прямой и плоскости. Появляется необходимость в проверке принадлежности прямой a плоскости α . Существует еще одно достаточное условие, при помощи которого доказывается параллельность.

При заданной прямой a с помощью уравнения двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 , плоскостью α — общим уравнением плоскости A x + B y + C z + D = 0 .

Необходимым и достаточным условием для параллельности прямой a и плоскости α яляется отсутствие решений системы линейных уравнений, имеющей вид A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 .

Из определения следует, что прямая a с плоскостью α не должна иметь общих точек, то есть не пересекаться, только в этом случае они будут считаться параллельными. Значит, система координат О х у z не должна иметь точек, принадлежащих ей и удовлетворяющих всем уравнениям:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 , а также уравнению плоскости A x + B y + C z + D = 0 .

Следовательно, система уравнений, имеющая вид A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 , называется несовместной.

Верно обратное: при отсутствии решений системы A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не существует точек в О х у z , удовлетворяющих всем заданным уравнениям одновременно. Получаем, что нет такой точки с координатами, которая могла бы сразу быть решениями всех уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 и уравнения A x + B y + C z + D = 0 . Значит, имеем параллельность прямой и плоскости, так как отсутствуют их точки пересечения.

Система уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A x + B y + C z + D = 0 не имеет решения, когда ранг основной матрицы меньше ранга расширенной. Это проверяется теоремой Кронекера-Капелли для решения линейных уравнений. Можно применять метод Гаусса для определения ее несовместимости.

Доказать , что прямая x — 1 = y + 2 — 1 = z 3 параллельна плоскости 6 x — 5 y + 1 3 z — 2 3 = 0 .

Для решения данного примера следует переходить от канонического уравнения прямой к виду уравнения двух пересекающихся плоскостей. Запишем это так:

x — 1 = y + 2 — 1 = z 3 ⇔ — 1 · x = — 1 · ( y + 2 ) 3 · x = — 1 · z 3 · ( y + 2 ) = — 1 · z ⇔ x — y — 2 = 0 3 x + z = 0

Чтобы доказать параллельность заданной прямой x — y — 2 = 0 3 x + z = 0 с плоскостью 6 x — 5 y + 1 3 z — 2 3 = 0 , необходимо уравнения преобразовать в систему уравнений x — y — 2 = 0 3 x + z = 0 6 x — 5 y + 1 3 z — 2 3 = 0 .

Видим, что она не решаема, значит прибегнем к методу Гаусса.

Расписав уравнения, получаем, что 1 — 1 0 2 3 0 1 0 6 — 5 1 3 2 3

1 — 1 0 2 0 3 1 — 6 0 1 1 3 — 11 1 3

1 — 1 0 2 0 3 1 — 6 0 0 0 — 9 1 3 .

Отсюда делаем вывод, что система уравнений является несовместной, так как прямая и плоскость не пересекаются, то есть не имеют общих точек.

Делаем вывод, что прямая x — 1 = y + 2 — 1 = z 3 и плоскость 6 x — 5 y + 1 3 z — 2 3 = 0 параллельны, так как было выполнено необходимое и достаточное условие для параллельности плоскости с заданной прямой.

Ответ: прямая и плоскость параллельны.

Видео:Семинар №7 "Прямая и плоскость в пространстве"Скачать

Доказать что прямая x 3t 2 y 4t 1 z 4t 5 параллельна плоскости

1.Знать уравнения прямой и уравнения плоскости, формулы вычисления угла между прямыми, между прямой и плоскостью, между плоскостями; формулы вычисления расстояния от точки до прямой и от точки до плоскости.

2.Уметь применять данные знания при решении задач, пояснять решения, отстаивать свою точку зрения, опираясь на отличное знание теории, работать в группе, проявлять активность и творчество.

3.Обеспечить в ходе урока воспитание целеустремленности, настойчивости, коммуникативных качеств личности, ораторских способностей и чувства времени.

Оборудование, наглядные пособия : ПК учащихся, интерактивная доска, инструмент доски, сканер, доска, мел, раздаточный материал, листы А3, по два на каждую группу.

Тип урока: Урок комплексного применения знаний и способов деятельности.

Цель урока : Усвоение умений самостоятельно в комплексе применять знания, умения и навыки, осуществлять их перенос в новые условия.

Методы и формы: КСО, элементы проблемного обучения, групповая работа, деловая игра «Рынок возможностей»

I . Организационный момент. Презентация 1,слайды -1, 2. — 3мин

II . Актуализация знаний и способов деятельности, необходимых для творческого применения. Проверка домашнего задания. Проверка знаний: «Лови ошибку! » — 4 мин. Презентация 1, слайды 3-5.

III . Обобщение и систематизация знаний и способов деятельности

«Презентация знаний » — 9мин.

IV . Применение обобщенных знаний и умений в новых условиях.

« Знания в дело!» Презентация 1, слайды 6-9. -5мин.

V . Освоение образца комплексного применения знаний и умений.

«Путь к вершине знаний» Презентация 1, слайды 10-12— 10 мин.

VI Комплексное применение знаний и умений.

«Путь к вершине успеха» Презентация 1, слайды 13-15-10мин

Подведение итогов урока. Рефлексия-3мин.

VIII Задание на дом.

Информация о домашнем задании.-1мин.

I . Организационный момент.

« Добрый день, господа! Рада Вас видеть и предлагаю начать работу по применению знаний по теме: «Взаимное расположение прямых и плоскостей в координатах». На доске Презентация 1. – Название темы урока.

Успехов вам и хорошего настроения!»

Вам предлагается «Рынок возможностей» по применению рассмотренных ранее уравнений прямой и плоскости и их взаимного расположения в координатах.

В конкурсе принимают участие три группы предпринимателей, которым предстоит пройти лестницу к вершине успеха.

«Путь к вершине знаний»

«Путь к вершине успеха»

На первой ступени испытание- «Лови ошибку!», на второй – «Презентация знаний» по теме, которая вам достанется по жребию, на третьей – три испытания: «Знания в дело!», « Путь к вершине знаний», « Путь к вершине успеха». Вершины достигает группа, набравшая максимальное число баллов.

Завершающий этап – инструктаж: «Как удержаться на вершине успеха».

II . Актуализация знаний и способов деятельности, необходимых для творческого применения. Проверка домашнего задания. Проверка знаний: «Лови ошибку! ». На обсуждение в группе 1 мин, на защиту решения – 3 мин (по 1 мин каждой команде). По одному представителю от каждой команды, после обсуждения в группе выходят к доске и исправляют ошибки.

Цена задания – 3 балла. Цена дополнения – 1 балл (снимается со счета команды, если другая команда сделала существенное дополнение).

На ПК учащихся и 3-5слайдах – задания с ошибкой. Повторение и закрепление уравнения прямой и плоскости.

1. Уравнение плоскости, проходящей через точку М (2; 1; -2) перпендикулярно вектору n4; -5; 7, имеет вид: 2( x — 4) + 1( y + 5) — 2( z – 7) = 0.

2. Уравнение прямой, проходящей через точку М (2; 3; -1), параллельно вектору p4; 7; -2, имеет вид: .

3. Прямая, проходящая через точку М (0; 2; 4), параллельная вектору p-3; 0; 5, имеет вид: x =-3 t , y = t +2, z =4+5 t .

III . Обобщение и систематизация знаний и способов деятельности

«Презентация знаний » -9мин.

От каждой группы выходит представитель и тянет жребий – название темы, по которой группа будет делать свой мини-проект. Мини-проект выполняется на 2 листах формата А3 в течение двух минут.

Доклад у доски – презентация конспекта темы занимает не более 2 минут, с учетом вопросов выступающим.

Требования к конспекту: краткость, наглядность, к каждому случаю чертеж, формула для вычисления угла, доступность, последовательность и четкость объяснения. Подведение итогов. Максимальное количество баллов – 5. Цена дополнения – 1 балл (снимается с команды, если существенное дополнение).

IV . Применение обобщенных знаний и умений в новых условиях.

« Знания в дело!». Путь к вершине – результат удачного применения знаний. Нарушение регламента – минус 1 балл. После каждого этапа IV – VI — подведение итогов. Задачи решаются на интерактивной доске (защита решений). На доклад по каждой задаче уровня А по 0,5 мин, уровня В по 1мин, на задачи уровня С по 2,5 мин. Докладчик представляет краткие записи плана решения с устными пояснениями к нему.