Как доказать, что четырехугольник — параллелограмм? Для этого можно использовать определение либо один из признаков параллелограмма.
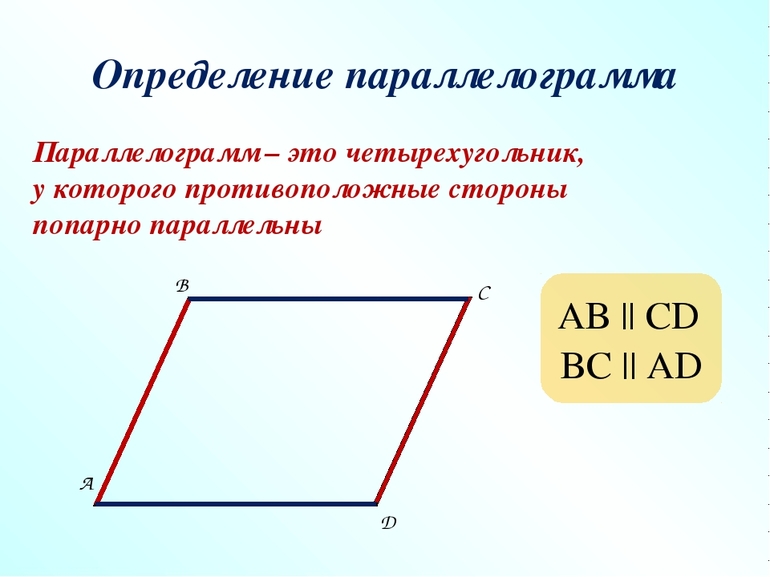
1) Четырехугольник является параллелограммом по определению, если у него противолежащие стороны параллельны, то есть лежат на параллельных прямых.
ABCD — параллелограмм, если
Для доказательства параллельности прямых используют один из признаков параллельности прямых, чаще всего — через внутренние накрест лежащие углы. Для доказательства равенства внутренних накрест лежащих углов можно доказать равенство пары треугольников.
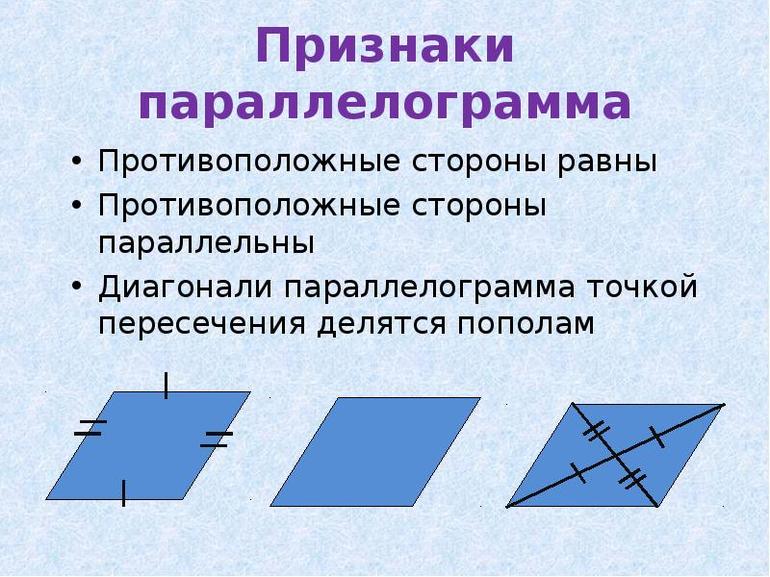
2) Четырехугольник является параллелограммом, если у него диагонали в точке пересечения делятся пополам.
Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AO=OC, BO=OD.
3) Четырехугольник является параллелограммом, если у него противолежащие стороны параллельны и равны.
Чтобы использовать этот признак параллелограмма, надо сначала доказать, что AD=BC и AD ∥ BC (либо AB=CD и AB ∥ CD).
Для этого можно доказать равенство одной из тех же пар треугольников.
Чтобы воспользоваться этим признаком параллелограмма, нужно предварительно доказать, что AD=BC и AB=CD.
Для этого доказываем равенство треугольников ABC и CDA или BCD и DAB.
Это — четыре основных способа доказательства того, что некоторый четырехугольник — параллелограмм. Существуют и другие способы доказательства. Например, четырехугольник — параллелограмм, если сумма квадратов его диагоналей равна сумме квадрату сторон. Но, чтобы воспользоваться дополнительными признаками, надо их сначала доказать.
Доказательство с помощью векторов или координат также опирается на определение и признаки параллелограмма, но проводится иначе. Об этом речь будет вестись в темах, посвященных векторам и декартовым координатам.
- Доказать, что четырехугольник ABCD — параллелограмм, если А (8 ; — 3), В (2 ; 5), С (10 ; 11), В (16 ; 3)?
- ABCD — параллелограмм, O — точка пересечения его диагоналей?
- ABCD – параллелограмм, O – точка пересечения диагоналей данного параллелограмма Saod = 7, 5 найти Sabcd = ?
- Даны координаты вершин четырехугольника ABCD : А (–6 ; 1), В (0 ; 5), С (6 ; –4), D (0 ; –8)?
- Дан параллелограмм АВСDКоординаты точек : А(3 ; — 7), С( — 5 ; — 1), точка О — пересечение диагоналейНайти : Координаты точки О — ?
- Даны координаты вершин четырехугольника ABCD : А (–6 ; 1), В (0 ; 5), С (6 ; –4), D (0 ; –8)?
- Точка пересечения диагоналей четырехугольника ВСКМ не является середингй одной из них?
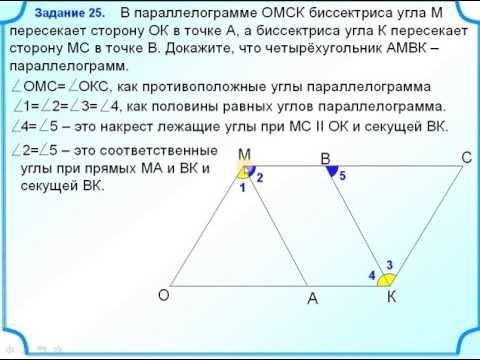
- Доказать , что четырехугольник , полученный при пересечении биссектрис углов параллелограмма , является параллелограммом?
- Точка пересечения диагоналей четырехугольника ABCM является центром его симметрии ?
- Помогите пожалуйста решить?
- Точка пересечения диагоналей 4 угольника является его центром симметрии ?
- Как доказать, что четырехугольник является параллелограммом?
- Определение параллелограмма
- Свойства фигуры
- Основные признаки
- Пошаговое доказательство
- 🎬 Видео
Видео:№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Доказать, что четырехугольник ABCD — параллелограмм, если А (8 ; — 3), В (2 ; 5), С (10 ; 11), В (16 ; 3)?
Геометрия | 5 — 9 классы
Доказать, что четырехугольник ABCD — параллелограмм, если А (8 ; — 3), В (2 ; 5), С (10 ; 11), В (16 ; 3).
Найти координаты точки пересечения его диагоналей.
Координаты проекций на оси длина
AB = (|2 — 8| ; |5 — ( — 3)|) = (6 ; 8) АВ = √(6 ^ 2 + 8 ^ 2) = 10
BC = (|10 — 2| ; |11 — 5)|) = (8 ; 6) ВC = √(8 ^ 2 + 6 ^ 2) = 10
CD = (|16 — 10| ; |3 — 11)|) = (6 ; 8) ВC = √(6 ^ 2 + 8 ^ 2) = 10
DA = (|8 — 16| ; | — 3 — 3)|) = (8 ; 6) ВC = √(8 ^ 2 + 6 ^ 2) = 10
длина всех сторон 10
свойство параллелограмма : противоположные стороны попарно равны
более того — этто ромб ( похож на квадрат)
диагонали — это АС и BD — точка пересечения М
координаты точки пересечения его диагоналей (т .
Xm = (Xa + Xc) / 2 = (8 + 10) / 2 = 9
Ym = (Ya + Yc) / 2 = ( — 3 + 11) / 2 = 4
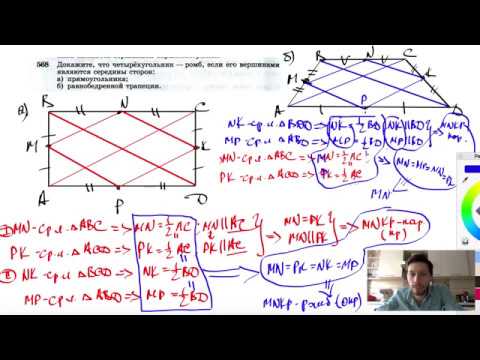
Видео:№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать
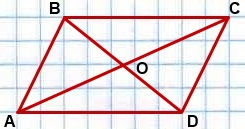
ABCD — параллелограмм, O — точка пересечения его диагоналей?
ABCD — параллелограмм, O — точка пересечения его диагоналей.
Найти площадь параллелограмма, если площадь треугольника ABO равна 7, 5 см.
Видео:Задание 25 Доказать, что четырёхугольник параллелограмм Определение параллелограммаСкачать
ABCD – параллелограмм, O – точка пересечения диагоналей данного параллелограмма Saod = 7, 5 найти Sabcd = ?
ABCD – параллелограмм, O – точка пересечения диагоналей данного параллелограмма Saod = 7, 5 найти Sabcd = ?
Видео:№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

Даны координаты вершин четырехугольника ABCD : А (–6 ; 1), В (0 ; 5), С (6 ; –4), D (0 ; –8)?
Даны координаты вершин четырехугольника ABCD : А (–6 ; 1), В (0 ; 5), С (6 ; –4), D (0 ; –8).
Докажите, что ABCD – прямоугольник, и найдите координаты точки пересечения его диагоналей.
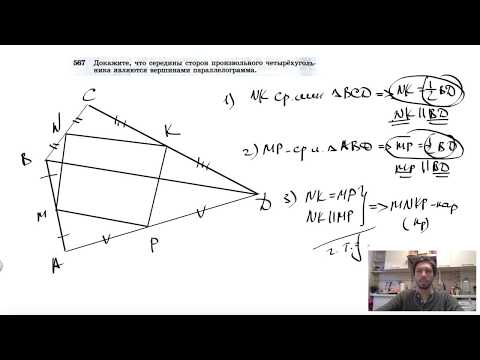
Видео:№567. Докажите, что середины сторон произвольного четырехугольника являютсяСкачать
Дан параллелограмм АВСDКоординаты точек : А(3 ; — 7), С( — 5 ; — 1), точка О — пересечение диагоналейНайти : Координаты точки О — ?
Дан параллелограмм АВСD
Координаты точек : А(3 ; — 7), С( — 5 ; — 1), точка О — пересечение диагоналей
Найти : Координаты точки О — ?
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Даны координаты вершин четырехугольника ABCD : А (–6 ; 1), В (0 ; 5), С (6 ; –4), D (0 ; –8)?
Даны координаты вершин четырехугольника ABCD : А (–6 ; 1), В (0 ; 5), С (6 ; –4), D (0 ; –8).
Докажите, что ABCD – прямоугольник, и найдите координаты точки пересечения его диагоналей.
Видео:№950. Докажите, что четырехугольник MNPQ является параллелограммом,Скачать

Точка пересечения диагоналей четырехугольника ВСКМ не является середингй одной из них?
Точка пересечения диагоналей четырехугольника ВСКМ не является середингй одной из них.
Может ли этот четырехугольник быть параллелограммом?
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Доказать , что четырехугольник , полученный при пересечении биссектрис углов параллелограмма , является параллелограммом?
Доказать , что четырехугольник , полученный при пересечении биссектрис углов параллелограмма , является параллелограммом.
Видео:Геометрия Докажите, что середины сторон четырехугольника являются вершинами параллелограммаСкачать
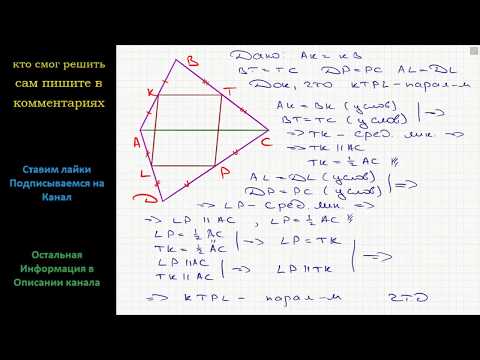
Точка пересечения диагоналей четырехугольника ABCM является центром его симметрии ?
Точка пересечения диагоналей четырехугольника ABCM является центром его симметрии .
Докажите что ABCM — параллелограмм.
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Помогите пожалуйста решить?
Помогите пожалуйста решить.
Даны координаты вершин четырёхугольника ABCD.
A ( — 6, 1) ; В (0, 5) ; С (6, — 4) ; D (0 ; — 8) Доказать что ABCD прямоугольник, и найдите координаты точки пересечение точки пересечения его диагоналей.
Видео:Доказательство первого признака параллелограммаСкачать

Точка пересечения диагоналей 4 угольника является его центром симметрии ?
Точка пересечения диагоналей 4 угольника является его центром симметрии .
Доказать что четырехугольник параллелограмм.
На этой странице сайта вы найдете ответы на вопрос Доказать, что четырехугольник ABCD — параллелограмм, если А (8 ; — 3), В (2 ; 5), С (10 ; 11), В (16 ; 3)?, относящийся к категории Геометрия. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.
1) б, т. К. 30 * 2 = 60 2) в, т. К. 120 / 2 = 60 3) б, т. К. 90 — 55 = 35 4) а 5) в, т. К. 180 — 140 = 40.
Вектора перпендикулярны, если их скалярное произведение равно нулю. Запишем скалярное произведение : — 2x + 12 = 0, отсюда x = 6.
1)углы при основании равны т. К. треугольник р / б. (равнобедренный) 2)вершина = 180 — внешний угол = 180 — 130 = 50т. К. они смежные 3)любой угол при основании = (180 — 50) : 2 = 65т. К углы при основании равны и сумма углов треугольника = 180 О..
Вот весь ответ. Надеюсь, помогла.
Ответ 2) в ромб1 из углов равен 90 то квадр.
Сначала проводим касательную к окружности, затем хорду и радиус ОС. Схема и расчет — в приложении.
Ответ : 10 см Объяснение : Дано : АВСМ — трапеция, АВ⊥АМ, ВС = 8 см, ∠ВСМ = 150°. СН — высота. Найти СН. ΔСМН — прямоугольный, ∠МСН = 150 — 90 + 60°, ∠М = 90 — 60 = 30°значит, СН = 1 / 2 СМ как катет, лежащий против угла 30 градусовСН = 20 : 2 = 1..
Самое основное в этой задаче понять, почему треугольник BCD — равнобедренный. Вспомни накрест лежащие углы, они равны при параллельных прямых и секущей третьей. А треугольник является равнобедренным, если его углы при основании равны. Основанием т..
Длина СД = АВ * 5 = 4, 3 * 5 = 21, 5 см АВ + СД = 4, 3 + 21, 5 = 25, 8 см.
Видео:Признаки параллелограмма Доказательство признаков параллелограммаСкачать

Как доказать, что четырехугольник является параллелограммом?
Видео:№951. Докажите, что четырехугольник ABCD является прямоугольником, и найдите егоСкачать

Определение параллелограмма
Четырехугольник является параллелограммом с параллельными противоположными сторонами. Эта фигура имеет по 2 тупых и острых угла, произвольную величину которых определяют при решении задач. Для этого используют не только признаки параллелограмма или треугольника, но и таблицу синусов с косинусами.
Квадрат, прямоугольник и ромб — это параллелограммы, обладающие общими свойствами. Фигура, у которой диагонали совпадают с биссектрисами, является ромбом. Согласно определению, прямоугольник — это четырехугольник, имеющий все прямые углы. Если стороны этой фигуры равны между собой, то прямоугольник является квадратом.
Параллелограмм — геометрическая фигура с равными противоположными сторонами. Если каждую из них возвести в квадрат и сложить их между собой, то полученная величина будет равна сумме квадратов диагоналей, проведенных через противоположные вершины углов фигуры. Диагонали этого четырехугольника пересекаются в точке, определить которую позволяют прямоугольные координаты.
Видео:8 класс, 4 урок, ПараллелограммСкачать

Свойства фигуры
Зная различные свойства четырехугольников, можно решать простые и сложные задачи по геометрии, начиная с определения периметра, заканчивая нахождением координаты вершины параллелограмма. Для решения задач используют 7 основных свойств параллелограмма, учитывая что его стороны попарно образуют:
- смежные углы, сумма которых составляет 180 градусов;
- равные отрезки;
- одинаковые по величине противоположные углы;
- четырехугольник, сумма углов которого равна 360 градусов;
- фигуру, диагонали которой пересекаются в точке, разделяющей их на 2 равных отрезка;
- равнобедренный треугольник, одна из сторон которого является биссектрисой фигуры;
- симметричные фигуры, дополняемые линией, проходящей через точку пересечения диагоналей.
Доказать последнее свойство позволяет II признак равенства треугольников. Известен отрезок, принадлежащий линии, проведенной через точку, в которой пересекаются диагонали. В четырехугольнике КМРТ он обозначен НП. Отсюда следует равенство треугольников КОП и НОР, поэтому НО=ОП.
Сумма смежных углов параллелограмма составляет 180 градусов, поскольку они являются односторонними при параллельных прямых. Существует свойство равенства острого угла и образованного высотами тупого угла четырехугольника АВСД. Параллелограмм имеет смежные углы А и Д, а высоты ВМ и ВН проведены из вершины В, поэтому угол МВН в сумме с Д равен 180 градусам.
Доказательство равенства противолежащих сторон и углов фигуры заключается в следующем. Например, диагонали ABCD делят фигуру на 2 равных треугольника, имеющих общую сторону в виде диагонали BD. При этом углы ADВ и ABC при противолежащих вершинах A и C являются накрест лежащими.
Параллелограмм состоит из равных треугольников ABD, BCD и ABC, ACD, образуемых диагоналями AC и ВD, значит AB=CD и AD=BC. Отсюда углы при вершинах A и C, В и D имеют одинаковую величину.
Свойства можно представить в виде формул для решения уравнений и примеров, а также доказать теоретически. Их следует запомнить, чтобы правильно применять на практике. Для решения более сложных задач по геометрии следует доказать основные свойства фигуры.
Видео:№379. Из вершин В и D параллелограмма ABCD, у которого АВ ≠ ВС и угол А острый, проведеныСкачать

Основные признаки
Существует 5 признаков параллелограмма, доказательство которых основано на свойствах прямых и образованных ими углов либо фигур. Выпуклый четырехугольник, вершины которого обозначены МНКП, имеет диагонали МП и НК. Признаки того, что фигура МНКП представляет собой параллелограмм, следующие:
- попарное равенство противоположных сторон: МН=КП и НК=МП;
- попарное равенство противоположных углов: МНК=КПМ и НКП=НМП;
- равенство и параллельность противоположных сторон: МН=КП и МН||КП;
- пересечение диагоналей в точке, которая делит их пополам;
- МН2 + КП2 = МН2 + НК2 + КП2 + МП2
Если четырехугольник имеет 2 равные и параллельные стороны, то он представляет собой параллелограмм. Четырехугольник MNPK имеет параллельные и равные MN и KP, отсюда следует доказательство I признака:
- Если провести диагональ MP, то она образует треугольники MNP и MPK.
- Фигуры имеют общую сторону MP, а MN=KP по условию.
- Поскольку прямая MP пересекает параллельные прямые MN и PK, то образуемые этими прямыми накрест лежащие углы равны.
- Параллельность других сторон MK и NP при диагонали MP основана на равенстве накрест лежащих углов, поэтому четырехугольник MNPK — параллелограмм.
Если четырехугольник имеет противоположные стороны, которые равны попарно, то он является параллелограммом. Перед тем как доказать, что фигура является параллелограммом, следует провести диагонали. Пошаговое доказательство II признака:
- Диагональ, проведенная через вершины фигуры АМКД А и К, образует 2 треугольника АМК и АКД.
- Поскольку согласно данным АМ=КД и АД=МК, а сторона АК — общая, значит, треугольники АМК и АКД имеют 3 равные стороны.
- Углы АКМ и АКД при параллельных прямых АМ и KД, пересекаемых диагональю АК, соответствуют по величине как накрест лежащие.
- По II признаку параллельность прямых АМ и КД, которые равны по условию, позволяет утверждать, что фигура АМКД является параллелограммом.
Доказать деление точкой пересечения каждой из диагоналей фигуры АМКД на равные отрезки позволяет II признак равенства треугольников. При этом AОД и КОМ равны. Следовательно, AО=КО и АО=ДО.
Согласно III признаку, четырехугольник, диагонали которого пересекаются, а точка пересечения делит их пополам, представляет собой параллелограмм. В четырехугольнике MNPQ она обозначена буквой К. Поскольку в ней пересекаются диагонали MP и NQ, то образуемые ими треугольники MNК и КPQ равны по I признаку. Это следует из равенства вертикальных углов MКN и PКQ, а также MК и NК, КP и КQ, которые равны по условию.
В треугольниках MNК и КPQ стороны MN и PQ равны между собой. Углы NMК и КPQ равны как накрест лежащие при MN и PQ и секущей MP. Отсюда следует, что прямые MN||PQ. Итак, четырехугольник MNPQ — это параллелограмм по I признаку, поскольку MN и PQ равны и параллельны.
Видео:Параллелограмм. Практическая часть - решение задачи. 8 класс.Скачать

Пошаговое доказательство
Перед тем как доказать, что четырехугольник параллелограмм, нужно провести высоты треугольников МНК и МПК, пересекающие МК в точках О и С. По данным задачи, МНК, МПК и НПК имеют одинаковые площади. Доказательство параллельности МК и НП состоит из следующих шагов:
- Равенство высот НО и ПС следует из соответствия площадей треугольников МНК и МПК, у которых имеется общая сторона МК.
- Прямые, содержащие высоты НО и ПС, пересекают прямую МК под углом 90 градусов.
- Точки пересечения лежат на одной и той же стороне относительно МК.
- Отсюда следует, что МК и НП — параллельны.
Чтобы доказать, что МН и ПК параллельны, нужно опустить из вершин треугольников МНК и НКП высоты Н и П, которые пересекут прямую ПК в точках Р и Т. По построению НР=ПТ, а по указанному условию площади треугольников МНК и НПК совпадают. Сторона МН параллельна ПК, следовательно, МНПК — параллелограмм. Итак, порядок доказательства параллельности МН и ПК аналогичен с доказательством, что МК и НП параллельны.
Доказательство признака образования равнобедренного треугольника и трапеции при пересечении противолежащей стороны параллелограмма биссектрисой АМ одного из углов состоит из следующих утверждений:
- Этот признак следует из свойства биссектрисы и равенства накрест лежащих углов при параллельных прямых AD и BC и луче АМ.
- Поэтому AМCD — трапеция с параллельными сторонами AD и МC.
- Отсекаемый биссектрисой АМ треугольник АВМ является равнобедренным.
- Стороны АВ и ВМ треугольника имеют одинаковую длину.
Зная, как доказать, что фигура параллелограмм, если известно, что 2 из его сторон равны и параллельны, можно использовать I признак равенства для доказательства другого. Согласно II признаку, стороны параллелограмма попарно равны между собой.
🎬 Видео
Найдите вершину A параллелограмма ABCD, если B(3; −4; 7), C(−5; 3; −2) и D(1; 2; −3)Скачать

№378. Докажите, что параллелограмм является выпуклым четырехугольником.Скачать

8 класс. Геометрия. Четырехугольник: вершины, стороны, диагонали. Свойства параллелограмма. Урок #1Скачать

Задача, которую боятсяСкачать