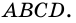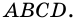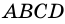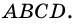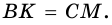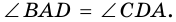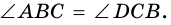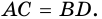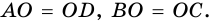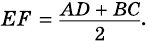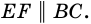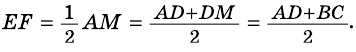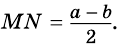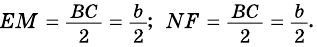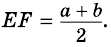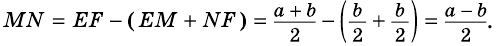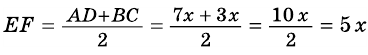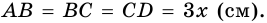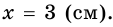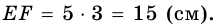Теорема: Если четырехугольник является трапецией, то ее:
а) средняя линия параллельна основаниям и равна их полусумме;
б) площадь равна произведению средней линии на высоту.
Доказательство.
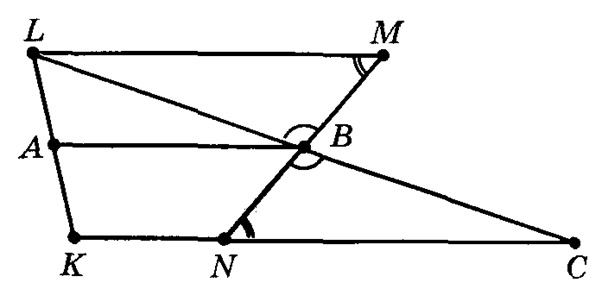
а) Пусть АВ — средняя линия трапеции KLMN.
Проведем прямую LB, пусть она пересекает прямую KN в точке С. Треугольники LBM и CBN равны, так как у них углы LBM и CBN равны как вертикальные, углы LMB и CNB равны как накрест лежащие при параллельных LM и КС, пересеченных прямой MN, стороны NB и MB равны по условию. Поэтому отрезки LB и ВС равны. Значит, АВ — средняя линия треугольника KLC, а отрезок АВ параллелен отрезку КС и, значит, основанию трапеции KN. А поскольку основания KN и LM параллельны, то средняя линия АВ параллельна и основанию LM. Мы доказали, что средняя линия трапеции параллельна обоим основаниям трапеции. Докажем теперь, что она равна полусумме этих оснований.
В соответствии с теоремой о средней линии треугольника получаем:
Но КС = KN + NC, a NC = LM, поэтому
АВ = 1/2 (KN + NC) = 1/2 (KN + LM) =1/2(KN+LM).
б) Мы знаем, что площадь трапеции равна произведению полусуммы ее оснований на высоту. Но, не забывайте о том, что полусумма оснований равна средней линии. Поэтому площадь трапеции равна произведению средней линии на высоту.
Видео:№951. Докажите, что четырехугольник ABCD является прямоугольником, и найдите егоСкачать

Задача 30718 Доказать, что четырехугольник ABCD -.
Условие
Доказать, что четырехугольник ABCD — трапеция, если A(3,6), B(5,2), C(-1, -3), D(-5,5).
Решение
По определению трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Так как даны координаты точек, будем искать координаты векторов, задающих стороны трапеции.
Векторы коллинеарны ( лежат на параллельных прямых), если их координаты пропорциональны.
vector и vector коллинеарны.
2:(-4)=(-4):8
vector и vector не коллинеарны.
Видео:№371. Докажите, что выпуклый четырехугольник ABCD является параллелограммом,Скачать

Трапеция и ее свойства с определением и примерами решения
Содержание:
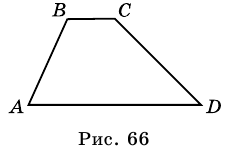
Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
На рисунке 66 изображена трапеция
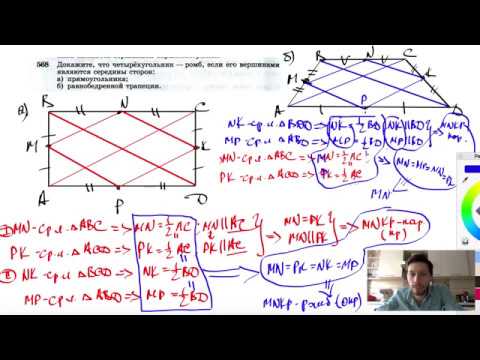
Видео:№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать
Свойства трапеции
Рассмотрим некоторые свойства трапеции.
1. Сумма углов трапеции, прилежащих к боковой стороне, равна 180°.
Так как 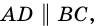
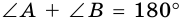
2. Трапеция является выпуклым четырехугольником.
Поскольку 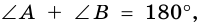
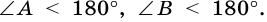
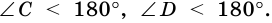
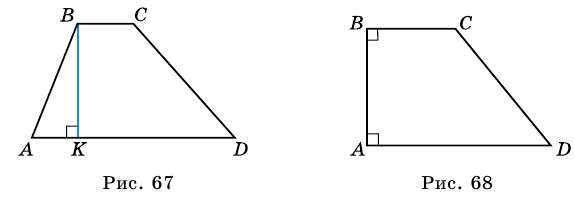
Высотой трапеции называют перпендикуляр, проведенный из любой точки основания трапеции к прямой, содержащей другое ее основание.
Как правило, высоту трапеции проводят из ее вершины. На рисунке 67 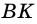
Трапецию называют прямоугольной, если один из ее углов -прямой. На рисунке 68 — прямоугольная трапеция 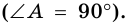
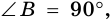
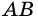
Трапецию называют равнобокой, если ее боковые стороны равны. На рисунке 69 — равнобокая трапеция
Видео:Геометрия Четырехугольник ABCD и AMKD – параллелограммы (см. рис.). Докажите, что четырехугольникСкачать

Свойства равнобокой трапеции
Рассмотрим некоторые важные свойства равнобокой трапеции.
1. В равнобокой трапеции углы при основании равны.
Доказательство:
1) Пусть в трапеции 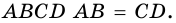
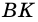
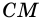
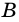
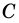
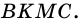
2) 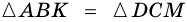
3) Также 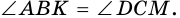
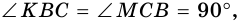
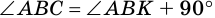
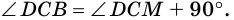
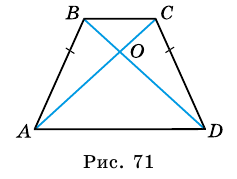
2. Диагонали равнобокой трапеции равны.
Доказательство:
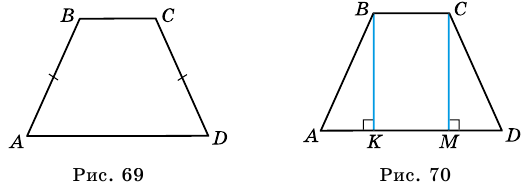
Рассмотрим рисунок 71. 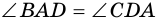
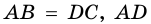
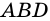
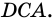
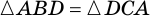
Пример:
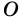
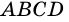
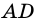
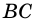
Доказательство:
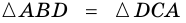
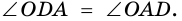
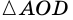
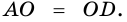
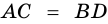
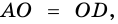
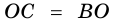
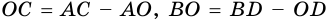
Теорема (признак равнобокой трапеции). Если в трапеции углы при основании равны, то трапеция — равнобокая.
Доказательство:
1) Пусть в 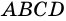
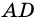
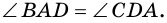
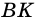
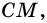
2) Тогда 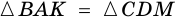
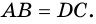
Термин «трапеция» греческого происхождения (по-гречески «трапед-зион» означает «столик», в частности столик для обеда; слова «трапеция» и «трапеза» — однокоренные).
В «Началах» Евклид под термином «трапеция» подразумевал любой четырехугольник, не являющийся параллелограммом. Большинство математиков Средневековья использовали термин «трапеция» с тем же смыслом.
Трапеция в современной трактовке впервые встречается у древнегреческого математика Посидония (I в.), но начиная только с XVIII в. этот термин стал общепринятым для четырехугольников, у которых две стороны параллельны, а две другие — не параллельны.
Видео:№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать

Свойство средней линии трапеции
Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.
Рассмотрим свойство средней линии трапеции.
Теорема (свойство средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть 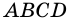
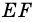
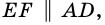
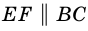
1) Проведем луч 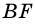
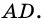
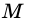
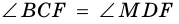
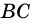
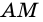
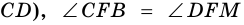
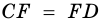
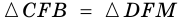
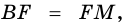
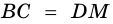
2) Поскольку 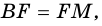
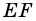
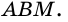
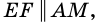
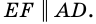
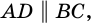
3) Кроме того,
Пример:
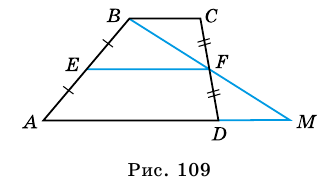
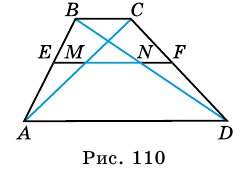
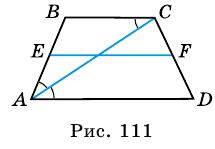
Докажите, что отрезок средней линии трапеции, содержащийся между ее диагоналями, равен полуразности оснований.
Доказательство:
Пусть 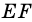
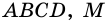
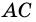
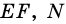
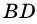
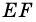
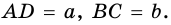
1) Так как 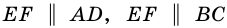
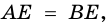
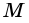
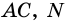
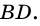
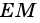
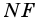
Тогда
2) 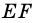
3)
Пример:
В равнобокой трапеции диагональ делит острый угол пополам. Найдите среднюю линию трапеции, если ее основания относятся как 3 : 7, а периметр трапеции — 48 см.
Решение:
Пусть 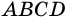
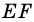
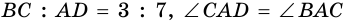
1) Обозначим 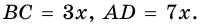
2) 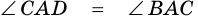
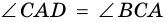
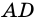
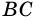
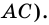
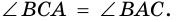
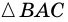
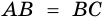
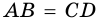
3) Учитывая, что 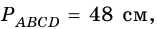
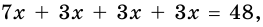
4) Тогда
То, что средняя линия трапеции равна полусумме оснований, было известно еще древним египтянам; эту информацию содержал папирус Ахмеса (примерно XVII в. до н. э.).
О свойстве средней линии трапеции знали также и вавилонские землемеры; это свойство упоминается и в трудах Герона Александрийского (первая половина I в. н. э.).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Площадь трапеции
- Центральные и вписанные углы
- Углы и расстояния в пространстве
- Подобие треугольников
- Площадь параллелограмма
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
💥 Видео
Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

№950. Докажите, что четырехугольник MNPQ является параллелограммом,Скачать

№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

8 класс, 6 урок, ТрапецияСкачать

№388. Докажите, что в равнобедренной трапеции: а) углы при каждом основании равныСкачать

ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Средняя линия треугольника и трапеции. 8 класс.Скачать

Геометрия Сторона AD четырехугольника ABCD является диаметром окружности, описанной около негоСкачать

№90. Вершины А и В трапеции ABCD лежат в плоскости α, а вершины С и D не лежат в этой плоскости. КакСкачать

8 класс, 15 урок, Площадь трапецииСкачать

Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

№341. Основанием четырехугольной пирамиды с вершиной Р является трапеция ABCDСкачать
Геометрия Диагонали равнобокой трапеции ABCD (AB=CD) пересекаются в точке O. Докажите, что AO=ODСкачать