Для того чтобы в выпуклый четырехугольник можно было вписать окружность должно

Видео:ЧЕТЫРЕХУГОЛЬНИК и ОКРУЖНОСТЬ | ЕГЭ Математика | @matematikajСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
4. Около любого треугольника можно ___________________________.
5. Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
6. Центром вписанной в треугольник окружности является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника.

1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

1. Описанная около треугольника

окружность изображена на рисунке:

1. Вписанная в четырехугольник окружность изображена на рисунке:

1. В треугольник можно вписать только _________________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
3. В четырехугольник можно вписать окружность, если __________________________________________________________.
4. В любой треугольник можно ___________________________.
5. Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
6. Центром описанного около окружности треугольника является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника

1. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

— ; — AB+CD=BC+AD;

— ; — AD·BC=AB·CD.

1. Вписанная в треугольник

окружность изображена на рисунке:

1. Описанная около четырехугольника окружность изображена на рисунке:

1. Около треугольника можно описать только ____________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
4. Около любого треугольника можно ___________________________.
5. Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
6. Центром вписанной в треугольник окружности является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника.

1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

1. Описанная около треугольника

окружность изображена на рисунке:

1. Вписанная в четырехугольник окружность изображена на рисунке:

1. В треугольник можно вписать только _________________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
3. В четырехугольник можно вписать окружность, если __________________________________________________________.
4. В любой треугольник можно ___________________________.
5. Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
6. Центром описанного около окружности треугольника является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника

1. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

— ; — AB+CD=BC+AD;

— ; — AD·BC=AB·CD.

1. Вписанная в треугольник

окружность изображена на рисунке:

1. Описанная около четырехугольника окружность изображена на рисунке:

1. Около треугольника можно описать только ____________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
4. Около любого треугольника можно ___________________________.
5. Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
6. Центром вписанной в треугольник окружности является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника.

1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

1. Описанная около треугольника

окружность изображена на рисунке:

1. Вписанная в четырехугольник окружность изображена на рисунке:

1. В треугольник можно вписать только _________________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
3. В четырехугольник можно вписать окружность, если __________________________________________________________.
4. В любой треугольник можно ___________________________.
5. Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
6. Центром описанного около окружности треугольника является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника

1. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

— ; — AB+CD=BC+AD;

— ; — AD·BC=AB·CD.

1. Вписанная в треугольник

окружность изображена на рисунке:

1. Описанная около четырехугольника окружность изображена на рисунке:

1. Около треугольника можно описать только ____________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
4. Около любого треугольника можно ___________________________.
5. Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
6. Центром вписанной в треугольник окружности является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника.

1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

1. Описанная около треугольника

окружность изображена на рисунке:

1. Вписанная в четырехугольник окружность изображена на рисунке:

1. В треугольник можно вписать только _________________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
3. В четырехугольник можно вписать окружность, если __________________________________________________________.
4. В любой треугольник можно ___________________________.
5. Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
6. Центром описанного около окружности треугольника является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника

1. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

— ; — AB+CD=BC+AD;

— ; — AD·BC=AB·CD.

1. Вписанная в треугольник

окружность изображена на рисунке:

1. Описанная около четырехугольника окружность изображена на рисунке:

1. Около треугольника можно описать только ____________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
4. Около любого треугольника можно ___________________________.
5. Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
6. Центром вписанной в треугольник окружности является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника.

1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

1. Описанная около треугольника

окружность изображена на рисунке:

1. Вписанная в четырехугольник окружность изображена на рисунке:

1. В треугольник можно вписать только _________________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
3. В четырехугольник можно вписать окружность, если __________________________________________________________.
4. В любой треугольник можно ___________________________.
5. Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
6. Центром описанного около окружности треугольника является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника

1. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

— ; — AB+CD=BC+AD;

— ; — AD·BC=AB·CD.

1. Вписанная в треугольник

окружность изображена на рисунке:

1. Описанная около четырехугольника окружность изображена на рисунке:

1. Около треугольника можно описать только ____________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
4. Около любого треугольника можно ___________________________.
5. Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
6. Центром вписанной в треугольник окружности является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника.

1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

1. Описанная около треугольника

окружность изображена на рисунке:

1. Вписанная в четырехугольник окружность изображена на рисунке:

1. В треугольник можно вписать только _________________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
3. В четырехугольник можно вписать окружность, если __________________________________________________________.
4. В любой треугольник можно ___________________________.
5. Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
6. Центром описанного около окружности треугольника является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника

1. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

— ; — AB+CD=BC+AD;

— ; — AD·BC=AB·CD.

1. Вписанная в треугольник

окружность изображена на рисунке:

1. Описанная около четырехугольника окружность изображена на рисунке:

1. Около треугольника можно описать только ____________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
4. Около любого треугольника можно ___________________________.
5. Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
6. Центром вписанной в треугольник окружности является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника.

1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

1. Описанная около треугольника

окружность изображена на рисунке:

1. Вписанная в четырехугольник окружность изображена на рисунке:

1. В треугольник можно вписать только _________________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
3. В четырехугольник можно вписать окружность, если __________________________________________________________.
4. В любой треугольник можно ___________________________.
5. Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
6. Центром описанного около окружности треугольника является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника

1. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

— ; — AB+CD=BC+AD;

— ; — AD·BC=AB·CD.

1. Вписанная в треугольник

окружность изображена на рисунке:

1. Описанная около четырехугольника окружность изображена на рисунке:

1. Около треугольника можно описать только ____________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
4. Около любого треугольника можно ___________________________.
5. Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
6. Центром вписанной в треугольник окружности является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника.

1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

1. Описанная около треугольника

окружность изображена на рисунке:

1. Вписанная в четырехугольник окружность изображена на рисунке:

1. В треугольник можно вписать только _________________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
3. В четырехугольник можно вписать окружность, если __________________________________________________________.
4. В любой треугольник можно ___________________________.
5. Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
6. Центром описанного около окружности треугольника является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника

1. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

— ; — AB+CD=BC+AD;

— ; — AD·BC=AB·CD.

1. Вписанная в треугольник

окружность изображена на рисунке:

1. Описанная около четырехугольника окружность изображена на рисунке:

1. Около треугольника можно описать только ____________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
4. Около любого треугольника можно ___________________________.
5. Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
6. Центром вписанной в треугольник окружности является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника.

1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

1. Описанная около треугольника

окружность изображена на рисунке:

1. Вписанная в четырехугольник окружность изображена на рисунке:

1. В треугольник можно вписать только _________________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
3. В четырехугольник можно вписать окружность, если __________________________________________________________.
4. В любой треугольник можно ___________________________.
5. Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
6. Центром описанного около окружности треугольника является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника

1. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

— ; — AB+CD=BC+AD;

— ; — AD·BC=AB·CD.

1. Вписанная в треугольник

окружность изображена на рисунке:

1. Описанная около четырехугольника окружность изображена на рисунке:

1. Около треугольника можно описать только ____________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
4. Около любого треугольника можно ___________________________.
5. Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
6. Центром вписанной в треугольник окружности является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника.

1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

1. Описанная около треугольника

окружность изображена на рисунке:

1. Вписанная в четырехугольник окружность изображена на рисунке:

1. В треугольник можно вписать только _________________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
3. В четырехугольник можно вписать окружность, если __________________________________________________________.
4. В любой треугольник можно ___________________________.
5. Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
6. Центром описанного около окружности треугольника является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника

1. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

— ; — AB+CD=BC+AD;

— ; — AD·BC=AB·CD.

1. Вписанная в треугольник

окружность изображена на рисунке:

1. Описанная около четырехугольника окружность изображена на рисунке:

1. Около треугольника можно описать только ____________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
4. Около любого треугольника можно ___________________________.
5. Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
6. Центром вписанной в треугольник окружности является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника.

1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

1. Описанная около треугольника

окружность изображена на рисунке:

1. Вписанная в четырехугольник окружность изображена на рисунке:

1. В треугольник можно вписать только _________________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
3. В четырехугольник можно вписать окружность, если __________________________________________________________.
4. В любой треугольник можно ___________________________.
5. Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
6. Центром описанного около окружности треугольника является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника

1. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

— ; — AB+CD=BC+AD;

— ; — AD·BC=AB·CD.

1. Вписанная в треугольник

окружность изображена на рисунке:

1. Описанная около четырехугольника окружность изображена на рисунке:

1. Около треугольника можно описать только ____________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то окружность называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то многоугольник называется ______________________________.
3. Вокруг четырехугольника можно описать окружность, если __________________________________________________________.
4. Около любого треугольника можно ___________________________.
5. Центр окружности, описанной около треугольника, лежит в точке пересечения __________________________________________.
6. Центром вписанной в треугольник окружности является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника.

1. Для того, чтобы в выпуклый четырехугольник можно было вписать окружность, должно выполняться следующее равенство:

1. Описанная около треугольника

окружность изображена на рисунке:

1. Вписанная в четырехугольник окружность изображена на рисунке:

1. В треугольник можно вписать только _________________________.

Тест по теме: «Вписанная и описанная окружности» (8 класс)

1. Если все стороны многоугольника касаются окружности, то многоугольник называется ________________________________.
2. Если все вершины многоугольника лежат на окружности, то окружность называется ______________________________.
3. В четырехугольник можно вписать окружность, если __________________________________________________________.
4. В любой треугольник можно ___________________________.
5. Центр окружности, вписанной в треугольник, лежит в точке пересечения __________________________________________.
6. Центром описанного около окружности треугольника является точка пересечения:

— Серединных перпендикуляров к сторонам треугольника

1. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

— ; — AB+CD=BC+AD;

— ; — AD·BC=AB·CD.

1. Вписанная в треугольник

окружность изображена на рисунке:

1. Описанная около четырехугольника окружность изображена на рисунке:

1. Около треугольника можно описать только ____________________.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

СРОЧНО. дам 50 баллов
Помогите решить тест
Тест по геометрии «Описанная окружность»

Если все вершины многоугольника лежат на окружности, то окружность называется _____________ около этого многоугольника, а многоугольник _________________ в эту окружность

Если сумма противоположных углов четырехугольника равна 180о, то ___________________ можно ____________ окружность.

3. Около какого треугольника можно описать окружность?

г) все варианты верны

4. Сколько окружностей можно описать около треугольника:

г) Не в любой треугольник можно вписать окружность

5. Центром описанной около треугольника окружности является точка пересечения:

а) Биссектрис треугольника

б) Высот треугольника

в) Медиан треугольника

г) Серединных перпендикуляров к сторонам треугольника.

6. Для того, чтобы вокруг выпуклого четырехугольника можно было описать окружность, должно выполняться следующее равенство:

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Окружность, вписанная в четырехугольник

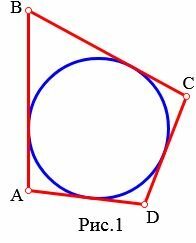
Определение 1. Окружность называют вписанным в четырехугольник, если окружность касается всех сторон четырехугольника.

На рисунке 1 окружность вписан в четырехугольник ABCD. В этом случае говорят также, что четырехугольник описан около окружности.

Теорема 1. Если окружность вписан в четырехугольник, то сумма противолежащих сторон четырехугольника равны.

Доказательство. Пусть окружность ABCD вписан в четырехугольник (Рис.2). Докажем, что ( small AB+CD=AD+BC ).

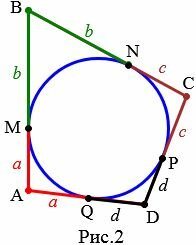Точки M, N, Q, P − точки касания окружности со сторонами четырехугольника. Так как отрезки касательных, проведенных к окружности через одну точку, равны (статья Касательная к окружности теорема 2), то

Из равенств (1) и (2), следует:

( small AB+CD=AD+BC. )

Теорема 2. Если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.

Доказательство. Пусть задан выпуклый четырехугольник ABCD и пусть ( small AB+CD=AD+BC. ) (Рис.3). Докажем, что в него можно вписать окружность.

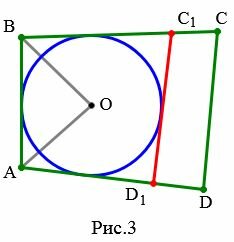Проведем биссектрисы углов A и B четырехугольника ABCD. Точку их пересечения обозначим буквой O. Тогда точка O равноудалена от сторон AB, BC, AD. Следовательно существует окружность с центром в точке O, которая касается этих трех сторон.

Пусть эта окружность не касается стороны CD. Тогда возможны два случая.

Случай 1. Сторона CD не имеет общих точек с построенной окружностью.

Проведем касательную C₁D₁ к окружности, параллельно стороне CD четырехугольника.

Тогда окружность с центром O вписан в четырехугольник ABC₁D₁. Следовательно, по теореме 1, имеем:

Но по условию данной теоремы:

Вычтем из равенства (4) равенство (3):

Получили, что в четырехугольнике CC₁D₁D длина одной стороны равна сумме длин трех остальных сторон, что невозможно (см. задачу 1 статьи Четырехугольник).

Таким образом сторона CD должна иметь общие точки с рассматриваемой окружностью.

Случай 2. Сторона CD имеет две общие точки с построенной окружностью (Рис.4).

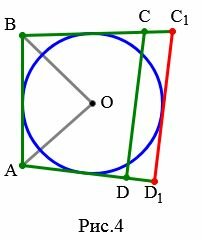Аналогичными рассуждениями можно показать, что сторона CD не может иметь две общие точки с построенной окружностью.

Следовательно, предполагая, что построенная окружность не касается стороны CD, мы пришли к противоречию. Таким образом, если в выпуклом четырехугольнике сумма противолежащих сторон равны, то в него можно вписать окружность.

Если в четырехугольник вписан окружность, то существует точка, равноудаленная от всех сторон четырехугольника. Эта точка является центром вписанной в четырехугольник окружности. Для нахождения этой точки достаточно найти точку пересечениия биссектрис двух соседних углов данного четырехугольника.

📸 Видео

Вписанная и описанная окружность в четырехугольник.Скачать

Что такое выпуклый четырёхугольник? | Математика 8 класс | Геометрия 8 класс | МегаШколаСкачать

Урок 1. Вписанная окружность в четырехугольник. Теория+ практикаСкачать

Вписанный в окружность четырёхугольник.Скачать

8 класс, 2 урок, Выпуклый многоугольникСкачать

Урок 14. Геометрия. Треугольник и окружность. Четырехугольник и окружность.Скачать

8 класс, 38 урок, Вписанная окружностьСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Вписанные и описанные окружности в четырёхугольникиСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

Шпаргалка к ЕГЭ по математике. Задание 6. Четырехугольник и окружность.Скачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Геометрия. 8 класс. Урок 6 "Вписанные четырехугольники"Скачать

Правильные треугольник, четырехугольник и шестиугольник (вывод основных формул)Скачать