Для того чтобы четырехугольник был ромбом необходимо

Страницы работы

Содержание работы

I. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ.

Необходимыми условиями правильности утверждения А называются такие условия, без соблюдения которых утверждение А заведомо не может быть верным.

Достаточными условиями правильности утверждения А называют условия, при которых утверждение А заведомо верно.

Приведем три примера.

1. Необходимым условием делимости целого числа N на 4 без остатка является четность числа N. Условие это необходимо, но не достаточно. Иначе говоря, если число N не является четным, оно не может делиться без остатка на 4, но если число N является четным, то это число может делиться на 4, а может и не делиться.

2. Достаточным условием того, что D АВС – равнобедренный, является условие равносторонности D АВС. Это условие достаточно: если D АВС равносторонний, то он заведомо равнобедренный, но не является необходимым, D АВС может быть равнобедренным, не будучи равносторонним.

3. Необходимым и достаточным условием того, что D АВС – прямоугольный является равенство а 2 +b 2 =с 2 , где а, b, с – длины сторон D АВС, причем с – длина наибольшей стороны.

Из определений необходимого и достаточного условий следует:

1. Если для правильности утверждения А необходимо утверждение В, то для правильности утверждения В достаточно утверждения А.

2. Если для правильности утверждения А достаточно утверждения В, то для правильности утверждения В необходимо утверждение А.

3. Если для правильности утверждения А необходимо утверждение В, то из того, что утверждение А верно, следует, что верно утверждение В: (А®В), и из того, что утверждение В неверно (ùВ), следует, что А также неверно (ùА): (ùВ®ùА).

4. Если для правильности утверждения А достаточно утверждения В, то из того, что утверждение В верно, следует, что верно утверждение А: (В®А), и из того, что утверждение А неверно следует, что и В – неверно: (ùА®ùВ).

5. Если для правильности утверждения А необходимо и достаточно утверждения В, то утверждения А и В тождественны, то есть (А«В), (ùА«ùВ), (АºВ).

Рассмотрим необходимое и достаточное условия принадлежности объекта к какому-то множеству.

] А Ì В, то есть множество А является подмножеством множества В. Тогда верны следующие утверждения (тождественные между собой):

1. Для того чтобы хÎВ, достаточно, чтобы хÎА (если хÎА, то хÎВ).

2. Для того чтобы хÎА, необходимо, чтобы хÎВ (опять, хÎА, то хÎВ). 3. Для того чтобы хÏВ необходимо, чтобы хÏА (если хÏВ, то хÏА).

4. Для того чтобы хÏА, достаточно, чтобы хÏВ (опять, если хÏВ, то хÏА).

Верно и обратное: если выполнено любое из четырех утверждений, то А Ì В.

Запишем условие «если хÎА, то хÎВ» в виде «из А следует В» или «А®В». Понятно, что А можно назвать причиной, В – следствием. Следствие «шире» причины.

Часто при формулировке каких-то условий вместо терминов «необходимо» и «достаточно» используются термины «только тогда» и «тогда».

Тождественными являются утверждения:

«для А необходимо В»

«А выполнено только тогда, когда выполнено В»

«из отсутствия В следует отсутствие А»

«для В достаточно А»

«В выполнено тогда, когда выполнено А»

Заучивать наизусть материал этого параграфа не рекомендуется. Надо сопоставить написанное выше с элементарными понятиями русского языка, составить простые примеры для себя лично, и в случае необходимости восстановить в памяти приведенный здесь материал.

Разберем несколько примеров.

Четырех угольник называется ромбом, если все его стороны равны.

Четырех угольник называется квадратом, если все его стороны равны, и все его углы – прямые.

Обозначим через А – множество всех квадратов, через В – множество всех ромбов. Очевидно, А Ì В (А есть подмножество В). Следовательно, можно сказать:

— для того чтобы четырехугольник был квадратом, необходимо, чтобы он был ромбом;

— для того чтобы четырехугольник был ромбом, достаточно, чтобы он был квадратом;

— если четырехугольник есть квадрат, то он есть ромб;

— если четырехугольник не есть ромб, то он не является квадратом.

2. Известно, что бабушка ходит в кино только на комедии.

Следовательно, можно сказать:

— для того чтобы бабушка пошла в кино, необходимо, чтобы там демонстрировали комедию;

— достаточным признаком того, что в зале демонстрируется комедия, является присутствие бабушки;

— если бабушка пошла в кино, то там демонстрируется комедия (но если бабушка не пошла в кино, то там может демонстрироваться что угодно, и комедия, и не комедия);

— если в кинотеатре не идет комедия, то там нет бабушки (но если в кинотеатре идет комедия, то бабушка может, как присутствовать, так и отсутствовать в зале).

2.. ПРОЦЕНТЫ. ФОРМУЛА СЛОЖНЫХ ПРОЦЕНТОВ И ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ.

Напомним, что процентом числа S называется сотая часть этого числа.

( 25% от S ) = 0,25 S

( 213% от S ) = 2,13 S

( g% от S ) =

При увеличении числа S на g % получим .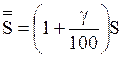

При уменьшении числа S на g % получим .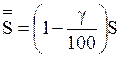

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Необходимые и достаточные условия

Понятие отношения следования между предложениями позволяет уточнить смысл слов «необходимо» и «достаточно», которые часто употребляются в математике.

Если из предложения А следует предложение В, то говорят, что В – необходимое условие для А, а А – достаточное условие для В.

Другими словами, предикат В(х) логически следует из предиката А(х), т.е. А(х)В(х), то А(х) называют достаточным условием для В(х), а В(х) – необходимым условием для А(х).

условие необходимости: АВ

условие достаточности: ВА

Если же предложения А и В равносильны, то говорят, что А – необходимое условие для В, и наоборот.

Другими словами, если из предиката А(х) логически следует предикат В(х), а из предиката В(х) логически следует предикат А(х), т.е. А(х)В(х), то А(х) – необходимое и достаточное условие для В(х), а В(х) – необходимое и достаточное условие для А(х).

условие необходимости и достаточности:

АВ

В начальном курсе математики слова «необходимо» и «достаточно», как правило, не употребляются, но зато широко используются их синонимы – «нужно» и «можно».

Приведем пример. В первой коробке 6 карандашей, во второй – на 2 меньше. Сколько карандашей в двух коробках?

Один из возможных путей поиска решения задачи может быть таким. Учитель спрашивает: можно ли сразу узнать, сколько карандашей (т.е. достаточно ли данных в задаче, чтобы сразу ответить на ее вопрос)?

Учащийся отвечает: нельзя, так как нужно знать, сколько карандашей во второй коробке (т.е. необходимо знать).

Учитель далее спрашивает: можно ли узнать количество карандашей во второй коробке? (т.е. достаточно ли данных в задаче, чтобы сразу ответить на этот вопрос)?

Ученик отвечает: можно.

Учитель спрашивает: что для этого нужно сделать? И т.д.

Правильное употребление слов «нужно» и «можно» – залог успеха в использовании слов «необходимо» и «достаточно» при дальнейшем изучении математики.

Рассмотрим следующие примеры.

1. Вместо многоточия вставим термины «необходимо», «достаточно» или «необходимо и достаточно»: «Для того чтобы число х являлось делителем числа 15, …, чтобы число х являлось делителем числа 5».

Решение: Введем обозначения: С(х) – «число х делитель числа 5», В(х) – «число х – делитель числа 15».

Для ответа на вопрос задачи нужно выяснить, каким условием является предикат С(х) для предиката В(х).

Для проверки достаточности предиката С(х) выясним, находятся ли С(х) и В(х) в отношении следования. Так как Т = , а Т = <1, 3, 5,15>, то Т Т и, следовательно, С(х)В(х). Истинность последнего высказывания означает, что С(х) является достаточным условием для В(х).

Проверим, является ли С(х) необходимым условием для В(х), выяснив, истинно ли высказывание В(х)С(х).

Так как найдется такое значение х (например, х = 3), при котором В(х) истинно, а С(х) ложно, то высказывание В(х)С(х) ложно и, следовательно, С(х) не является необходимым условием для В(х).

Таким образом, вместо многоточия можно вставить термин «достаточно»: «Для того чтобы число х являлось делителем числа 15, достаточно, чтобы х являлось делителем числа 5».

2. Дано предложение: «Для того чтобы четырехугольник был ромбом, необходимо, чтобы его диагонали были взаимно перпендикулярны». Выясним, нельзя ли сформулировать это предложение по-другому.

Поскольку предложение «Диагонали ромба взаимно перпендикулярны» вытекает из предложения «Четырехугольник – ромб», то предложение «Для того чтобы четырехугольник был ромбом, необходимо, чтобы его диагонали были взаимно перпендикулярны» можно сформулировать еще так:

1) Из того, что четырехугольник – ромб, следует, что его диагонали взаимно перпендикулярны.

2) Во всяком ромбе диагонали взаимно перпендикулярны.

3) Если четырехугольник – ромб, то его диагонали взаимно перпендикулярны.

4) Чтобы диагонали четырехугольника были взаимно перпендикулярны, достаточно, чтобы он был ромбом.

3. Вставить слова «необходимо», «достаточно», «необходимо и достаточно» в предложение «Для того чтобы натуральное число делилось на 6, …, чтобы оно делилось на 2».

Решение: Пусть предложение А – «число делится на 6», В – «Число делится на 2». Тогда, для того чтобы выполнялось условие необходимости, из предложения А должно логически следовать предложение В, а чтобы выполнялось условие достаточности – предложение А должно логически следовать из В.

Действительно, любое число, которое делится на 6, делится на 2. Значит, выполняется условие необходимости. И не верно, что любое число, делящееся на 2, делится на 6 (например, 14 делится на 2, но не делится на 6).

Значит, условие достаточности не выполняется, а вместо многоточия нужно вставить термин «необходимо»: «Для того чтобы натуральное число делилось на 6, необходимо, чтобы оно делилось на 2».

Видео:№568. Докажите, что четырехугольник — ромб, если его вершинами являются середины сторон:Скачать

Для того чтобы четырехугольник был ромбом необходимо

Замечено, что автор разделяет понятия «необходимость» и «достаточность»
Естественно, что их надо разделять, без этого никак..

Русским языком.
Если А необходимое условие для В, то если А — неверно, то В точно неверно. Или наоборот — если В верно, то значит верно и А (A ⇐ B).
Если А достаточное условие, то из верности А автоматически вытекает верность В (A ⇒ B).

Для примера.
Чтобы сдать экзамен по матану, необходимо сдать все расчетки. Т.е., если студент уже сдает экзамен, значит расчетки он уже сдал.
Чтобы сдать экзамен по матану, достаточно ответить на вопросы «на 3» из билета. Т.е., если студент отвечает на эти вопросы, то экзамен он сдаст.

Классический пример из школьной программы.

x0 — точка экстремума — > f'(x0)=0 — это необходимое условие
Но не достаточное, ибо f'(x0)=0 не обязательно влечет, что x0 — точка экстремума. Доказать в одну сторону получится, в другую — нет.

Чтобы x0 являлось точкой экстремума, достаточно, чтобы f'(x0)=0 и знак производной менялся в точке x0.
Здесь уже, если начать в доказательстве с того, что f'(x0)=0 и знак производной менялся в точке x0 — мы придем к тому, что x0 — точка экстремума.

Вообще в Никольской все хорошо расписано.
только предварительно надо прочитать про прямые и обратные теоремы, а также хорошо бы знать закон контрапозиции.
A=>B Заметим, что по закону контрапозиции A=>B эквивалентно ¬В=>¬A (если не В, то не А)
то есть если не будет В, то не будет и А или иначе без В нет А. Потому В — необходимое условие для А,
Эквивалентные формулировки для A=>B: для А необходимо В, В является необходимым условием для А.
Поэтому когда мы говорим: для того, чтобы А, необходимо В, то мы должны доказывать теорему A=>B

В теореме A=>B : А- достаточное условие для В, если выполняется А, то выполняется и В, для В достаточно А

Ну и вот когда мы доказываем теорему A B, то есть «для А необходимо и достаточно В», то доказательство из двух частей
1) для А необходимо В. Как сказано выше мы должны доказывать теорему A=>B
2) для А достаточно В . В этом случае В — достаточное условие для А, а это значит, мы должны доказать B=>A

А можешь привести пример, когда достаточное условие не является необходимым?

Так и с необходимыми и достаточными условиями
надо брать много теорем и анализировать устройство, давать разные эквивалентные формулировки: на языке «если. то. «, необходимое условие, достаточное условие

А ведь еще есть «если и только если»

🎦 Видео

Площадь ромба. Легче понять...Скачать

В четырехугольник вписан ромб, стороны которого параллельны диагоналям четырехугольника.Скачать

Площади четырехугольников: трапеция, параллелограмм, ромб. Геометрия на клеточке. ОГЭСкачать

Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

№1080. Докажите, что любой правильный четырехугольник является квадратом.Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

🤓ВАЖНО РЕШЕНИЕ, а не ответ #часть 1 #shorts #tutoronlineСкачать

Ромб, признаки. 8 класс.Скачать

Площади фигур. Сохраняй и запоминай!#shortsСкачать

Площадь ромба 📐 А бесплатный файлик в комментарияхСкачать

все свойства ромба #SHORTSСкачать

Четырехугольники. Вебинар | МатематикаСкачать

Параллелограмм. Свойства. Прямоугольник, ромб, квадрат. ЗАДАЧИСкачать

Один отрезок - диагональ четырёхугольника, диаметр окружности, высота ромбаСкачать

Площадь ромба равна 9. Одна из его диагоналей в 8 раз больше другой. Найдите меньшую диагональ.Скачать

необходимые и достаточные условияСкачать