Для того чтобы четырехугольник был прямоугольником достаточно чтобы (8 видео)

ПРАКТИЧЕСКАЯ РАБОТА. ОТНОШЕНИЯ СЛЕДОВАНИЯ И РАВНОСИЛЬНОСТИ МЕЖДУ ПРЕДЛОЖЕНИЯМИ

Цель. Уметь устанавливать отношения следования и равносильности между парами предложений, видеть связь с начальным курсом математики.

Теоретическая часть

Вопросы к изучению

1. Отношения следования между предложениями.

2. Отношения равносильности между предложениями.

Основные понятия темы

Ø отношение логического следования между предложениями;

Ø отношение равносильности между предложениями.

Обозначения

Þ – логическое следование;

Практическая часть

1. Следует ли предложение В(х) — «Число х четное» из предложения А (х), если: а) А(х) — «Число х делится на 6»; б) А(х) — «Число х делится на 7»; в) А(х) — «Число х делится на 2». Предложения А(х) и В(х) заданы на множестве натуральных чисел.

2. Установите, находятся ли данные пары предложений в отношении следования: а) Треугольник АВС — равносторонний. Треугольник АВС– равнобедренный; б) Четырехугольник АВСD — квадрат. Четырехугольник АВСD – ромб; в) х 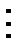3 и х 6; г) а>2 и а>5.

3. Полученные в упражнении 2 утверждения о следовании сформулируйте шестью различными способами.

4. Сформулируйте следующие высказывания в виде «если . то . »:

а) А — достаточное условие для В;

б) А — необходимое условие для В;

в) В -достаточное условие для А;

г) В — необходимое условие для А.

5. Среди следующих предложений укажите истинные; ответы обоснуйте:

а) Число а — натуральное, следовательно, и 15а — натуральное число.

б) Число 15а — натуральное, следовательно, а — натуральное число.

в) Если в четырехугольнике все углы прямые, то этот четырехугольник — прямоугольник.

г) Если в четырехугольнике диагонали равны, то этот четырехугольник — прямоугольник.

д) Для того чтобы четырехугольник был прямоугольником, достаточно, чтобы все его углы были равны.

е) Для того чтобы четырехугольник был прямоугольником, необходимо, чтобы все его углы были равны.

6. Для ложных высказываний из упражнения 5 постройте различными способами отрицание.

7. Равносильны ли следующие предложения А (х) и В(х), если: а) А(х) — «число делится на 9», В(х) — «сумма цифр в записи числа делится на 9»; б) А(х) — «каждое слагаемое суммы делится на 4», В(х) — «сумма делится на 4».

8. Какие из следующих предложений можно переформулировать, употребив слова «необходимо» либо «достаточно»: а) Если в четырехугольнике все углы равны, то четырехугольник является прямоугольником; б) Сумма двух четных чисел есть число четное; в) Всякое число, которое делится на 3 и на 5, делится на 15.

9. Какие из нижеприведенных высказываний истинные:

а) Для того, чтобы число делилось на 3, достаточно, чтобы оно делилось на 6.

б) Для того чтобы число делилось на 3, необходимо, чтобы оно делилось на 6.

в) Для того чтобы число делилось на 100, необходимо и достаточно, чтобы оно делилось на 10.

г) Для того чтобы число делилось на 10, необходимо и достаточно, чтобы оно делилось на 2 и на 5.

10. Вместо многоточия вставьте слова «необходимо» либо «достаточно», либо «необходимо и достаточно», чтобы данные предложения были истинными:

а) Для того чтобы сумма двух натуральных чисел делилась на 2, …, чтобы каждое слагаемое делилось на 2.

б) Для того чтобы каждое слагаемое делилось на 2, . , чтобы сумма этих слагаемых делилась на 2.

в) Для того чтобы число делилось на 45, . , чтобы оно делилось на 5 и на 9.

г) Для того чтобы угол был острым, . , чтобы он был меньше прямого.

1. Докажите, что предложение «в прямоугольнике Р диагонали взаимно перпендикулярны» и «прямоугольник Р — квадрат» равносильны. Утверждения о равносильности сформулируйте тремя различными способами.

2. Вставьте слова «и» либо «или» так, чтобы следующие высказывания были истинными: а) а × в =0 Û а =0 …в=0; б) а × в¹ 0 Û а¹ 0 …в¹ 0; в) х Î A В Û х Î А х Î В; г) хÏ А В Û х Ï А х Ï B.

3. В начальном курсе математики синонимом слова «необходимо» является слово «нужно» («надо»), и синонимом слова «достаточно» — слово «можно». Зная это, вставьте вместо многоточия слова: «нужно» либо «можно», так чтобы высказывания были истинными; ответы обоснуйте: а) Для того чтобы умножить сумму натуральных чисел на 5, … каждое слагаемое умножить на 5; б) Для того чтобы найти неизвестное слагаемое, . из суммы вычесть другое слагаемое; в) Для того чтобы вычесть число из суммы, . вычесть его из одного из слагаемых; г) Для того чтобы число было четным, . чтобы оно делилось на 2.

Дата добавления: 2021-01-26 ; просмотров: 269 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:№951. Докажите, что четырехугольник ABCD является прямоугольником, и найдите егоСкачать

Равносильности между предложениями

Рассмотрим две высказывательные формы: «число х кратно 4» и «число х кратно 2», заданные на множестве N натуральных чисел.

Как связаны между собой эти два предложения?

Можно сказать так: из того, что число х кратно 4, следует, что х кратно 2. Это мы можем утверждать, потому что знаем — при всех значениях х, при которых истинно предложение «число х кратно 4», истинно и предложение «число х кратно 2». В этом случае говорят, что данные предложения находятся в отношении логического следования.

Определение. Высказывательная форма В(х) следует из высказывательной формы А(х), если В(х) обращается в истинное высказывание при всех тех значенияхх, при которых А(х) истинна.

Если А и В — высказывания, тогда говорят, что из А следует В, если всякий раз, когда А истинно, истинно и В.

Для обозначения отношения логического следования используется знак =>. Соединяя две высказывательные формы А(х) и В(х) таким знаком, мы получаем высказывание А(х) => В(х), прочитать которое можно по разному:

3) Если Л (х), то В(х).

5) А(х) есть достаточное условие для В(х).

6) В(х) есть необходимое условие для А(х).

Например, утверждение о том, что из предложения «число х кратно 4», следует предложение «число х кратно 2», можно сформулировать еще так:

— Всякое число, которое кратно 4, кратно и 2.

— Если число кратно 4, то оно кратно и 2.

— Кратность числа 2 есть следствие кратности его 4.

— Кратность числа 4 есть достаточное условие для его кратности 2.

— Кратность числа 2 есть необходимое условие для его кратности 4.

Последние два предложения часто формулируют в следующей форме:

-Для того чтобы число было кратно 2, достаточно, чтобы оно было кратно 4.

-Для того чтобы число было кратно 4, необходимо, чтобы оно было кратно 2.

Так как одно и то же утверждение «из А(х) следует В(х)» можно прочитать по-разному, надо уметь переходить от одной его формулировки к другой, не меняя смысла.

Задача 1. Данные предложения переформулируйте, используя различные способы прочтения утверждения А(х) => В(х):

а) Всякий квадрат является прямоугольником.

б) Для того чтобы число делилось на 5, достаточно, чтобы его запись оканчивалась нулем.

Решение. а) В данном высказывании можно выделить два предложения: А(х) — «четырехугольник — квадрат» и В(х) — «четырехугольник — прямоугольник». Они находятся в отношении следования: А(х)ÞВ(х), которое выражено предложением со словом «всякий». Данное высказывание можно переформулировать:

1) Из того, что четырехугольник — квадрат, следует, что он прямоугольник.

2) Если четырехугольник — квадрат, то он прямоугольник.

3) Четырехугольник является прямоугольником — это следствие того, что четырехугольник — квадрат.

4) Для того чтобы четырехугольник был прямоугольником, достаточно, чтобы он был квадратом.

5) Для того чтобы четырехугольник был квадратом, необходимо, чтобы он был прямоугольником.

б) В данном высказывании так же, как и в а), можно выделить два предложения: Р(х) — «число делится на 5» и К(х) — «запись числа оканчивается нулем», причем второе является достаточным условием для первого. Поэтому имеет место следование: К(х) => Р(х), которое можно сформулировать так:

1) Из того, что запись числа оканчивается нулем, следует, что число делится на 5.

2) Всякое число, запись которого оканчивается нулем, делится на 5.

3) Если запись числа оканчивается нулем, то оно делится на 5.

4) Делимость числа на 5 — это следствие того, что его запись оканчивается нулем.

5) Для того чтобы запись числа оканчивалась нулем, необходимо, чтобы оно делилось на 5.

Как и любое высказывание, предложение А(х) => В(х) может быть истинным либо ложным. Но так как оно может быть сформулировано в виде «всякое А<х) есть В(х)», то его истинность устанавливается путем доказательства, а с помощью контрпримера — что оно ложно.

Задача 2. Определите значение истинности высказывания:

а) Если запись числа оканчивается цифрой 6, то число делится на 2.

б) Для того чтобы число делилось на 5, необходимо, чтобы его запись оканчивалась нулем.

Решение. а) По всей видимости это высказывание истинное. Действительно, всякое число, запись которого оканчивается цифрой 6 — четное, а всякое четное число делится на 2. Следовательно, число, запись которого оканчивается цифрой 6, делится на 2.

Мы убедились в истинности данного высказывания путем доказательства.

б) Если сформулировать данное высказывание в виде «из того, что число делится на 5, следует, что его запись оканчивается нулем», то сразу можно сказать, что оно ложное. И убедиться в этом можно при мощи контрпримера. Так, число 35 делится на 5, но его запись не оканчивается нулем.

С теоретико-множественной точки зрения высказывание А(х) => В(х)означает, что если Т_А — множество истинности высказывательной фомы А(х), а Т_В— множество истинности высказывательной формы В(х), то Т_А Ì Т_В. Справедливо и обратное утверждение.

Этим фактом удобно пользоваться при установлении значения истинности высказывания А(х) => В<х).

Задача 3. Доказать, что из уравнения Зх(х — 2) = 0 следует уравнение Зх(х — 2)(х + 3) = 0, если уравнения заданы на множестве Z целых чисел.

Решение. Множество решений первого уравнения – Т₁ = , множество решений второго – Т₂ = . Видим, что Т₁ Ì Т_2. Следовательно, из уравнения

Зх(х — 2) = 0 следует уравнение 3х(х-2)(х + 3) = 0.

Рассмотрим две высказывательные формы А(х) — «число делите» на 3» и В(х) — «сумма цифр в записи числа делится на 3». Из школьного курса математики известно, что если число делится на 3, то сумма цифр в записи этого числа разделится на 3, и наоборот. В этом случае говорят, что предложения А(х) и В(х) равносильны.

Определение. Предложения А(х)иВ(х)равносильны, если из предложенияА(х)следует предложениеВ(х), а из предложения В(х) следует предложениеА (х).

Для обозначения отношения равносильности используется знак . Соединяя две высказывательные формы А(х) и В(х) таким знаком, мы получаем высказывание А(х) В(х), прочитать которое можно по-разному:

2) А(х) тогда и только тогда, когда В(х).

3) А(х) — необходимое и достаточное условие для В(х).

4) В(х) — необходимое и достаточное условие для А(х).

Например, утверждение о том, что предложение «число делится на 3» и «сумма цифр в записи числа делится на 3» равносильны, можно сформулировать еще так:

-Число делится на 3 тогда и только тогда, когда сумма цифр в его записи делится на 3.

-Для того чтобы число делилось на 3, необходимо и достаточно, чтобы сумма цифр в его записи делилась на 3.

С теоретико-множественной точки зрения высказывание А(х) В(х) означает, что если Т_А — множество истинности высказывательной формы А(х), а Т_В— множество истинности высказывательной формы В(х),то Т_А = Т_В.

Задача 4. Доказать, что уравнения 3х(х — 2) = 0 и 3х(х — 2)(х + 3) = 0 равносильны на множестве целых неотрицательных чисел.

Решение. Множество решений первого уравнения — Т, = 2> множество решений второго, заданного на множестве целых неотрицательных чисел, Т₂= . Число -3 (см. задачу 3) множеству Т₂ не принадлежит, потому что оно не является целым неотрицательным. Имеем, что Т₁ = Т₂, следовательно, данные уравнения на множестве

целых неотрицательных чисел равносильны.

Заметим, что мы рассматриваем понятия логического следования и равносильности для одноместных высказывательных форм. Для предложений, содержащих две и более переменных, эти понятия определяются аналогично.

Отметим также, что знак мы использовали раньше, в частности, рассматривая логическую структуру явных определений понятий. Мы установили, что ее можно представить в виде аÛb. Употребление знака здесь не случайно. Дело в том, что определение, как говорят в математике, порождает два равносильных предложения, которые затем используются наряду с другими в доказательствах. Например, определение «квадратом называется прямоугольник, имеющий равные соседние стороны» порождает равносильные предложения: «если прямоугольник является квадратом, то в нем соседние стороны равны» и «если в прямоугольнике соседние стороны равны, то прямоугольник является квадратом». Использовать в доказательствах можно любое из этих двух.

Знак мы также использовали в записи правил построения отрицания высказываний. Например, Û В этом случае речь идет о равносильности высказываний определенной формы. При этом считают, что предложения равносильны, если они одновременно истинны, либо одновременно ложны. Другими словами, если их значения истинности совпадают при одинаковых наборах значений высказываний А и В.

Упражнения

1.Следует липредложение В(х) — «Число х четное» из предложения А(х), если:

а)А(х) — «Число х делится на 6»;

б)А<х) — «Число х делится на 7»;

в)А(х) — «Число х делится на 2».

Предложения А(х) и В(х) заданы на множестве натуральных чисел.

2.Установите, находятся ли данные пары предложений в отношении следования:

а)Треугольник АВС — равносторонний.

Треугольник АВС — равнобедренный.

б)Четырехугольник АВСБ — квадрат.

Четырехугольник АВСБ — ромб.

3. Полученные в упражнении 2 утверждения о следовании сформулируйте шестью различными способами.

4. Сформулируйте следующие высказывания в виде «если . то . »:

а)А — достаточное условие для В;

б)А — необходимое условие для В;

в)В — достаточное условие для А;

г)В- необходимое условие для А.

5.Среди следующих предложений укажите истинные; ответы обоснуйте:

а) Число а — натуральное, следовательно, и 15а — натуральное число

б) Число 15а — натуральное, следовательно, а — натуральное число

в) Если в четырехугольнике все углы прямые, то этот четырехугольник — прямоугольник.

г) Если в четырехугольнике диагонали равны, то этот четырехугольник — прямоугольник.

д) Для того чтобы четырехугольник был прямоугольником, достаточно, чтобы все его углы были равны.

е) Для того чтобы четырехугольник был прямоугольником, необходимо, чтобы все его углы были равны.

6. Для ложных высказываний из упражнения 5 постройте различными способами отрицание.

7. Равносильны ли следующие предложения А (х) и В(х), если:

а)А(х) — «число делится на 9»,

В(х) — «сумма цифр в записи числа делится на 9».

б)А(х) — «каждое слагаемое суммы делится на 4»,

В(х) — «сумма делится на 4».

8. Докажите, что предложение «в прямоугольнике Р диагонали взаимно перпендикулярны» и «прямоугольник Р — квадрат» равносильны. Утверждения о равносильности сформулируйте тремя различными способами.

9. Вставьте слова «и» либо «или» так, чтобы следующие высказывания были истинными:

10. Какие из следующих предложений можно переформулировать, употребив слова «необходимо» либо «достаточно»:

а) Если в четырехугольнике все углы равны, то четырехугольник является прямоугольником.

б) Сумма двух четных чисел есть число четное.

в) Всякое число, которое делится на 3 и на 5, делится на 15.

11. Какие из нижеприведенных высказываний истинные:

Для того чтобы число делилось на 3, достаточно, чтобы оно делилось на 6.

б) Для того чтобы число делилось на 3, необходимо, чтобы оно лепилось на 6 •

в) Для того чтобы число делилось на 100, необходимо и достаточно чтобы оно делилось на 10.

г) Для того чтобы число делилось на 10, необходимо и достаточно, чтобы оно делилось на 2 и на 5.

12.Вместо многоточия вставьте слова «необходимо» либо «достаточно», либо «необходимо и достаточно», чтобы данные предложения были истинными:

а) Для того чтобы сумма двух натуральных чисел делилась на 2, . чтобы каждое слагаемое делилось на 2.

б) Для того чтобы каждое слагаемое делилось на 2, . , чтобы сумма этих слагаемых делилась на 2.

в) Для того чтобы число делилось на 45, . , чтобы оно делилось на 5 и на 9.

г) Для того чтобы угол был острым. , чтобы он был меньше прямого.

13. В начальном курсе математики синонимом слова «необходимо» является слово «нужно» («надо»), и синонимом слова «достаточно» — слово «можно». Зная это, вставьте вместо многоточия слова: «нужно» либо «можно», так чтобы высказывания были истинными; ответы обоснуйте:

а) Для того чтобы умножить сумму натуральных чисел на 5, . каждое слагаемое умножить на 5.

б) Для того чтобы найти неизвестное слагаемое, . из суммы вычесть другое слагаемое.

в) Для того чтобы вычесть число из суммы. вычесть его из одного из слагаемых.

г) Для того чтобы число было четным. чтобы оно делилось на 2.

Не нашли, что искали? Воспользуйтесь поиском:

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Правила построения отрицаний.

Задания на формирование умения строить отрицания составных высказываний

Типовые задания с решениями

Пример 1.Сформулируйте высказывания соответствующие формулама) ; б) ; в) , если А – «гремит гром»; В – «моросит дождь».

а) АÙВ – «Гремит гром и моросит дождь».

Т.к. º , «Гром не гремит или дождь не моросит»

б) АÚВ – «Гремит гром или моросит дождь».

Т.к. º Ù , — «Гром не гремит и дождь не моросит»

в) АÞВ — «Если гремит гром, то моросит дождь»

Т.к. º А Ù , — «Гремит гром и не моросит дождь».

Задания для самостоятельной работы (базовый уровень)

1. Сформулируйте отрицания следующих высказываний двумя способами.

а) 3 и 8 – однозначные числа.

б) Собака домашнее или дикое животное.

в) Картофель и тыква овощи.

г)Число 0,7 натуральное или целое.

д) Хотя бы одна из букв в слове «дом» гласная.

Определите значения истинности данных высказываний и их отрицаний.

2. Сформулируйте отрицания следующих высказываний, пользуясь формулами:

в) число 6 делится на 2 и на 3;

г) В романе «Война и мир» 70 или более страниц;

д) ель – лиственное или хвойное дерево;

е) ель — лиственное и хвойное дерево.

Задания для самостоятельной работы (повышенный уровень)

5. Задания на формирование умений:

устанавливать логическое следование и равносильность между предложениями,

формулировать обратную, противоположную и обратную противоположной теоремы,

устанавливать необходимые и достаточные условия.

Типовые задания с решениями

Пример 1.Доказать, что:

а) предикат Q(х) – «натуральное число х делится на 5 » логически следует из предиката Р(х) – «натуральное число х делится на 15»;

б) предикат Q(х) – «х – нечетное число» не является логическим следованием предиката Р(х) – «х – простое число»;

в) предикаты Q(х) – «противоположные стороны четырехугольника попарно параллельны» и Р(х) – «противоположные стороны четырехугольника попарно равны» равносильны.

а) Для доказательства логического следования Р(х) ÞQ(х) достаточно показать, что Т 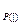Ì. Т Т.к. Т =, а Т =, то включение очевидноТ Ì. Т и требуемое утверждение доказано.

б) Для того доказать, что предикат Q(х) – «х – нечетное число» не является логическим следствием предиката Р(х) – «х – простое число», достаточно указать хотя бы один элемент, принадлежащий области ложности предиката Р(х) ÞQ(х), т.е. указать такое значение переменной х, при котором Р(х) обращается в истинное высказывание, а Q(х) – в ложное. В данном случае можно указать х=2, поскольку 2 число простое, но не является нечетным.

в) Для доказательства равносильности предикатов Р(х) и Q(х) достаточно показать, что Т = Т . По условию Т есть множество четырехугольников, противоположные стороны которых попарно параллельны, а Т — множество четырехугольников, противоположные стороны которых попарно равны. Поскольку в том и другом случае мы имеем дело с множеством параллелограммов, то и равносильность предикатов Р(х) и Q(х) можно считать доказанной.

Пример 2.Вместо многоточий вставить слова – «необходимо», «достаточно» или «необходимо и достаточно»:

а) для того, чтобы четырехугольник был ромбом, ……, чтобы его диагонали пересекались под прямым углом;

б) для того, чтобы сумма делилась на 19, ……, чтобы каждое слагаемое делилось на 19;

в) для того, чтобы треугольник был равнобедренным, ……, чтобы два внутренних угла его были равны.

а) Пусть Р(х) – «четырехугольник х — ромб», Q(х) – «диагонали четырехугольника х пересекаются под прямым углом». Сформулируем утверждение в виде импликации («х)( Р(х) ÞQ(х)): «Если четырехугольник ромб, то диагонали его пересекаются под прямым углом». Это высказывание истинно. Следовательно, Р(х)-достаточное условие для Q(х), а Q(х)-необходимое условие для Р(х).

Теперь сформулируем импликацию («х)( Q(х) Þ Р(х)): «Если диагонали четырехугольника пересекаются под прямым углом, то этот четырехугольник — ромб». Это высказывание ложно. Следовательно, условие Q(х) не является достаточным для Р(х), а Р(х) не является необходимым условием для Q(х).

Итак, Q(х)является необходимым условием для Р(х), но не является достаточным. Поэтому, вместо многоточия следует вставить слово «необходимо».

«Для того, чтобы четырехугольник был ромбом, необходимо, чтобы его диагонали пересекались под прямым углом».

б) Пусть Р(х) – «сумма х делится на 19», Q(х) – «каждое слагаемое суммы х делится на 19». Сформулируем утверждение в виде импликации («х)( Р(х) ÞQ(х)): « Если сумма чисел делится на 19, то каждое слагаемое этой суммы делится на 19».Последнее высказывание ложно. Следовательно, Р(х) не является условием достаточным для Q(х), а Q(х) не является необходимым для Р(х).

Теперь сформулируем импликацию («х)( Q(х) Þ Р(х)): «Если каждое слагаемое суммы делится на 19, то и вся сумма делится на 19».

Это высказывание истинно, а значит, Q(х) является условием, достаточным для Р(х), а Р(х) — необходимым для Q(х).

Итак, Q(х) является достаточным условием для Р(х), но не является необходимым. Поэтому вместо многоточия следует вставит слово «достаточно».

«Для того, чтобы сумма делилась на 19, достаточно, чтобы каждое слагаемое суммы делилось на 19».

в) Пусть Р(х) – «Треугольник х -равнобедренный», Q(х) –«Два внутренних угла треугольника х равны». Сформулируем утверждение в виде импликации («х)( Р(х) ÞQ(х)): «Если треугольник равнобедренный, то два внутренних угла его равны». Это утверждение является истинным, значит, Р(х) — достаточное условие для Q(х), а Q(х) – необходимое условие для Р(х).

Теперь сформулируем импликацию («х)( Q(х) Þ Р(х)): «Если внутренних угла треугольника, то этот треугольник равнобедренный». Это утверждение также является истинным, значит, Q(х) — достаточное условие для Р(х) , а Р(х)– необходимое условие для Q(х). Итак, Q(х) является необходимым и достаточным условием для Р(х), а значит, вместо многоточия следует вставит слова «необходимо и достаточно».

«Для того, чтобы треугольник был равнобедренным, необходимо и достаточно, чтобы два внутренних угла его были равны».

Пример 3.Выделить преамбулу, условие и заключение в теореме «В трапеции средняя линия параллельна основаниям». Сформулировать предложения: обратное, противоположное и обратное противоположному. Установит их истинность.

Решение. В теореме идет речь о множестве U — четырехугольников. Пуст х произвольно выбранный четырехугольник. Предикат Р(х) – « Четырехугольник х — трапеция» — условие теоремы, а предикат Q(х) – «Средняя линия четырехугольника х параллельна основаниям» — заключение теоремы. Тогда данную теорему можно символически записать в виде следующей импликации: («хÎ U)( Р(х) ÞQ(х)).

Здесь разъяснительная часть представлена квантором общности («хÎ U). В импликативной форме данную теорему можно сформулировать так; «Если четырехугольник – трапеция, то его средняя линия параллельна основаниям».

По определению, обратное предложение имеет логическую структуру («хÎ U)( Q(х) Þ Р(х)) и формулируется следующим образом: «Если средняя линия четырехугольника параллельна основаниям, то этот четырехугольник – трапеция». Последнее утверждение является ложным.

Предложение, противоположное данному имеет логическую структуру («хÎ U)( Þ и следующую формулировку: «Если четырехугольник – не является трапецией, то его средняя линия не параллельна основаниям» и также является ложным.

Предложение обратное противоположному, имеет логическую структуру («хÎU)( Þ и формулируется так: «Если средняя линия четырехугольника не параллельна основаниям, то этот четырехугольник – не трапеция».

Последнее утверждение является контрапозитивным прямой теореме и также истинно.

Задания для самостоятельной работы (базовый уровень)

1. На множестве Х= заданы предикаты: А(х): «Число х кратно 6» и В(х): «число х кратно 3».Укажите такие значения х, при которых:

а) предикаты А(х) и В(х) обращаются в истинные высказывания;

б) предикаты А(х) и В(х) обращаются в ложные высказывания.

2. На множестве Х= заданы предикаты: А(х): «Число х кратно 6» и В(х): «число х кратно 3». Сформулируйте импликацию А(х) ÞВ(х) и определите ее множество истинности. Можно ли утверждать что предикат В(х) следует из предиката А(х) на множестве Х?

3. На множестве Z – целых чисел задана импликация А(х) ÞВ(х): «Если число х больше 2, то оно положительное».

а) Найдите значение истинности этой импликации при х=3, х=1 и при х=-4.

б) Можно ли указать такое значение аÎХ, при котором А(а) истинно, а В(а) ложно?

в) Можно ли утверждать, что В(х) следует из А(х)?

г) Каково множество истинности импликации А(х) ÞВ(х)?

4. Докажите, что предикаты Р(х) – «Натуральное число х делится на 5» и Q(х) – «Десятичная запись натурального числа х оканчивается на 0 или 5» равносильны?

5. Докажите, что предикат Q(х) — «Натуральное число х делится на 13» логически следует из предиката Р(х) – «Натуральное число х делится на 26».

6.На множестве Х= заданы предикаты: А(х)- «(х-1)х=0»; В(х) – «х(х-1)(х-2)(х-3)=0.

а) Найдите их множество истинности и определите, в каком отношении эти множества находятся.

б) Верно ли, что А(х) логически следует из В(х)?

в) Можно ли утверждать, что А(х) – достаточное условие для В(х)? Если да, то сформулируйте предложение, используя термин «достаточно».

г) Можно ли утверждать, что В(х) – необходимое условие для А(х)? Если да, то сформулируйте предложение, используя термин «необходимо».

7. На множестве Z – целых чисел заданы предикаты: Д(х)-«х — делитель 12» и Е(х) – «х – делитель 36».

а) Докажите, что предикат Е(х) следует из предиката Д(х).

б) Сформулируйте предложение в виде «Если…., то»

в) Сформулируйте предложение с помощью слова «достаточно».

г) Сформулируйте предложение с помощью слова «необходимо».

8. Какие из следующих высказываний истинны:

а) Присутствие на всех занятиях по математике является достаточным условием для успешной сдачи экзамена по математике.

б) Наличие паспорта необходимо для приобретения билета на самолет.

в) Равенство числителя дроби нулю достаточно для равенства нулю всей дроби.

г) Достижение 18-летнего возраста необходимо для участия в выборах.

9. Сформулируйте следующие теоремы в импликативной форме, выделите разъяснительную часть, условие и заключение.

а) Диагонали прямоугольника равны.

б) Диагонали ромба взаимно-перпендикулярны.

в) Вертикальные углы равны.

г) В равнобедренном треугольнике углы при основании равны.

д) В правильный многоугольник можно вписать окружность.

е) Вписанный угол измеряется половиной дуги, на которую он опирается.

10. Для следующих теорем сформулируйте обратные, противоположные и обратные противоположным высказывания. Установите их истинность.

а) Если один из множителей делится на 23, то все произведение делится на 23. б) Если четырехугольник – ромб, то противоположные его углы равны.

в) Если число натуральное, то оно равно своему модулю.

г) Если треугольник правильный, то вокруг него можно описать окружность.

д) Если фигура квадрат, то она имеет центр симметрии.

е) Если дуги заключены между параллельными хордами, то они равны.

ж) Если фигура прямоугольник, то диагонали его точкой пересечения делятся пополам.

з) Если число представляется произведением трех последовательных натуральных чисел, то оно делится на 6.

и) Если дискриминант квадратного уравнения равен нулю, то это уравнение имеет два равных корня.

Задания для самостоятельной работы (повышенный уровень)

а) предикат А(х) обращаются в ложное высказывание, а предикат В(х) — в истинное высказывание;

б) предикат А(х) обращаются в истинное высказывание, а предикат В(х) — в ложное высказывание.

2. На множестве Х – учащихся школы заданы предикаты В(х): «Учащийся х — пионер» и А(х): «Учащийся х – член совета дружины».

а) Найти множество истинности предикатов А(х) и В(х).

б) Найдутся ли такие значения х, при которых А(х) обращается в истинное в высказывание, а В(х) – ложное.

в) Можно ли утверждать, что предикат В(х) следует из предиката А(х)?

г) Изобразите множества истинности предикатов А(х) и В(х) при помощи кругов Зйлера и укажите, в каком отношении эти множества находятся.

3.Докажите, что предикат D(х): «х =25», заданный на множестве R – действительных чисел, следует из предиката С(х): «х=5», заданного на том множестве.

Выясните, в каком отношении находятся множества истинности предикатов С(х) и D(х), изобразите их при помощи кругов Эйлера.

4.Предикаты А(х) и В(х) заданы на множестве Х. Множества их истинности обозначены Т и Т и соответственно и отношения между ними изображены на рисунке: