Длина окружности сечения шара плоскостью 6п расстояние от центра

Геометрия | 10 — 11 классы

На расстоянии 4 см от центра шара проведено сечение, длина окружности которого равна 6П см.

Найдите объём шара.

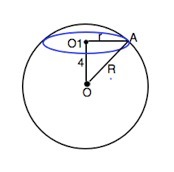
На прикрепленном рисункеОО1 = 4 см — расстояние от центра шара до центра сечения.

Радиус сечения, расстояние между центрами и радиус шара — прямоугольный треугольник ОАО1.

R = √(OO1² + OA²) = √25 = 5 см

V = 4πR³ / 3 = 4π•125 / 3 = 500π / 3 см³.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Точка А — центр шара, точка B — центр сечения шара, а точка С лежит на окружности сечения?

Точка А — центр шара, точка B — центр сечения шара, а точка С лежит на окружности сечения.

Длина какого отрезка — AC, BС или AB — равна расстоянию от точки А до плоскости сечения?

Видео:Длина окружности. Математика 6 класс.Скачать

Шар R радиус шара на расстоянии OO1 от центра проведено сечение угол между сечением и радиусом альфа Найти площадь сечения?

Шар R радиус шара на расстоянии OO1 от центра проведено сечение угол между сечением и радиусом альфа Найти площадь сечения.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Через точку на поверхности шара проведены два сечения шара плоскостями, равноудаленными от центра шара?

Через точку на поверхности шара проведены два сечения шара плоскостями, равноудаленными от центра шара.

Радиус шара равен 4, а расстояние от его центра до плоскостей сечений равно 2 корень из 3 .

Найдите градусную меру угла, образованного плоскостями сечений.

Видео:Длина окружности. Площадь круга, 6 классСкачать

Расстояние от центра до сечения шара 8 см, радиус сечения — 2 см?

Расстояние от центра до сечения шара 8 см, радиус сечения — 2 см.

Опрделите объём шара.

Видео:Сечение сферыСкачать

Шар пересечен плоскостью?

Шар пересечен плоскостью.

Площадь сечения равна 576пи см ^ 2.

Расстояние от центра шара до плоскости сечения равна 7 см.

Найдите площадь поверхности шара.

Видео:Окружность и круг, 6 классСкачать

В шаре на расстоянии 12см от его центра проведено сечение, площадь которого равно 64п см²?

В шаре на расстоянии 12см от его центра проведено сечение, площадь которого равно 64п см².

Найдите плошать поверхности шара!

Видео:№587. Расстояние от центра шара радиуса R до секущей плоскости равно d. Вычислите: а) площадь S сечеСкачать

Площадь сечения шара плоскостью равна 36 Пи см2?

Площадь сечения шара плоскостью равна 36 Пи см2.

Расстояние от центра до плоскости сечения 3 см Найдите объём шара.

Видео:Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

В шаре на расстоянии 4 см от центра проведено сечение , радиус которого 3 см?

В шаре на расстоянии 4 см от центра проведено сечение , радиус которого 3 см.

Найдите площадь поверхности шара.

Видео:11 класс, 19 урок, Сфера и шарСкачать

В шаре на расстоянии 4 см от центра проведено сечение, площадь которого 25П cм кв?

В шаре на расстоянии 4 см от центра проведено сечение, площадь которого 25П cм кв.

Найдите объем шара.

Видео:Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

В шаре, радиуса 10 см на расстоянии 6 см от центра проведено сечение плоскостью?

В шаре, радиуса 10 см на расстоянии 6 см от центра проведено сечение плоскостью.

Найдите площадь сечения.

На странице вопроса На расстоянии 4 см от центра шара проведено сечение, длина окружности которого равна 6П см? из категории Геометрия вы найдете ответ для уровня учащихся 10 — 11 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

1. ) BC = 5 2. ) AB = 16 3. ) AE = 14 4. ) 5. ) CE = 4. 5, PC = 13, 5 6. ) A1C = 10.

M = (a + b) / 2 31. 5 = (25 + b) / 2 31. 5 — 25 = b / 2 6. 5 = b / 2 b = 13.

35 + 35 = 70 70 — (10Х2) = 50см. Это и есть периметр параллелограмма. Шо тут фоткать? ))).

Угол ABC = 180 — (70 + 10) = 100 градусов. Угол ABD = Углу DBC = 50 градусов. Угол HBC = 180 — (90 + 70) = 20 градусов. Угол DBH = 50 — 20 = 30 градусов.

RovoeхорошистДля конуса верно : Sбок = пRL пRL = 60п RL = 60 10R = 60 R = 6см. Высота конуса равна : h = √ L ^ 2 — R ^ 2 h = √ (100 — 36) = 8 (см). Найдем радиус вписанного шара : pr = S S = 8 * 12 / 2 = 48 (см. Кв). р = (10 + 10 + 12) / 2 = 16(см..

Решение в файле .

1)120•2 = 240(действие в скопках, умножение первое) 2)240 / 40 = 6(действие в скопках, деление второе) 3)6 + 144 = 150(действие в скопках, сумма третья) 4)150 / 6 = 25(действие за скопками, четвёртое деление).

По условию (см. Фото) : О — центр сферы, ОА — радиус сферы. О1 — центр секущей плоскости, АО1 — радиус секущей плоскости r. ОО1 — расстояние от центра сферы до секущей плоскости, равное 3 см. С1 обозначим длину окружности секущей плоскости. С1 =..

Если угол 150, то острые углы по 30 град, проведенные высоты образуют треугольники прямоугольные. Их свойство — катет против угла в 30 град равен половине гипотенузы. Гипотенузы — стороны параллелограмма, значит 2m и 2n cоотаетственно.

Видео:Сечение шараСкачать

Контрольные работы (стр. 6 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8

3. Назовите элементы симметрии правильной че­тырехугольной пирамиды.

4*. Какими свойствами должен обладать усечен­ный конус, чтобы в него можно было вписать шар?

Вариант 2

1. Диагональ осевого сечения цилиндра равна 32 см и наклонена к плоскости его основания под углом 300. Найдите высоту и площадь основания ци­линдра.

2. Через вершину конуса, высота которого рав­на h, проведено сечение. Угол между плоскостями сечения и основания равен a. Угол при вершине се­чения равен 2b. Найдите радиус основания конуса.

3. Назовите элементы симметрии правильной шестиугольной пирамиды.

4*. Какими свойствами должна обладать пирамида, чтобы в нее можно было вписать сферу?

Видео:9 класс, 26 урок, Длина окружностиСкачать

Контрольная работа № 5

Видео:Тема 8. Шар. Сечение шара плоскостью. Объем шараСкачать

Вариант 1

1. Основанием прямого параллелепипеда являет­ся ромб, диагонали которого равны 24 см и 10 см. Угол между меньшей диагональю параллелепипеда и плоскостью основания равен 450. Найдите: а) объем параллелепипеда; б) его большую диагональ.

2. Длина окружности сечения шара плоскостью, удаленной от его центра на 3 см, равна 6π см. Най­дите объем и площадь поверхности шара.

3. Угол между плоскостью сечения прямого кру­гового конуса, проходящей через его вершину, и плоскостью его основания равен j. Хорда, являющая­ся основанием сечения, равна 2a и удалена от цент­ра основания конуса на расстояние, равное a. Най­дите: а) объем конуса; б) площадь его боковой по­верхности.

4*. Равнобедренный треугольник с углом при вершине 2j вращается вокруг прямой, параллельной его основанию и проходящей через его вершину. Вы­сота треугольника, проведенная к его основанию, равна h. Найдите: а) объем фигуры вращения; б) площадь ее поверхности.

Вариант 2

1. Основание прямой призмы A. C1 — равнобед­ренный треугольник, в котором AB=AC=17 см, BC=8 см. Угол между плоскостью, содержащей прямую BC и вершину A1, и плоскостью основания равен 300. Найдите: а) объем призмы; б) площадь сечения призмы указанной плоскостью.

2. Площадь сечения шара плоскостью равна 36p см2. Радиус шара, проведенный в точку окружности сечения, составляет с его плоскостью угол 450. Найдите объем и площадь поверхности шара.

3. Диагональ сечения прямого кругового ци­линдра плоскостью, параллельной его оси, равна 2a и наклонена к плоскости основания под углом . Расстояние от оси цилиндра до плоскости сечения равно a. Найдите: а) объем цилиндра; б) площадь его полной поверхности.

4*. Прямоугольный треугольник с катетами 3 см и 4 см вращается вокруг своей гипотенузы. Найдите: а) объем фигуры вращения; б) площадь ее поверхности.

Контрольная работа № 6

Вариант 1

1. Запишите разложение по координат­ным векторам векторов: а) (7,3,-6); б) (0,-1,4); в) (-1,0,4); г) (0,0,-2).

2. Найдите угол φ между векторами (1,2,-4) и (0,-1,3).

3. Найдите точку, расположенную в плоскостях Oyz и 7x+3y-5z-3=0 и имеющую координату z=3.

4. Составьте уравнение плоскости, проходящей через ось Ox и точку M (2,1,5).

5*. Под действием силы (1;-2;2), приложенной под углом 600 к направлению перемещения, тело переместилось на 10. Вычислите выполненную этой силой работу.

Вариант 2

1. Даны векторы (2,-1,4) и (3,0,-2). Най­дите координаты векторов: а) 5; б) 3—; в) 2+5.

2. Найдите угол φ между векторами (3,2,-2) и (0,4,4).

3. Найдите точку, расположенную в плоскостях 2x+5y+6z+4=0 и плоскости Oxy, имеющую ординату, равную 2.

4. Составьте уравнение плоскости, проходящей через ось Oz и точку N (4,-2,3).

5*. Три силы (4,-5,2), (1,0,-1), (-1,6,-3) приложены к одной точке. Вычислите, какую работу производит равнодействующая этих сил, когда ее точка приложения M1(4,3,2), двигаясь пря­молинейно, перемещается в точку M2(7,5,-3).

В1. 1. Да. 2. а) BC; б) EF. 4. 4. 5*. 10. В2. 1. Да. 2. а) BC; б) AF. 4. 6. 5*. 10.

В1. 1. Прямая c может быть параллельна прямым a и b; может пересекать каждую из прямых a и b; может скрещиваться с каждой из них. 3. а) Параллельны или скрещиваются с b; б) пересекаются, параллельны или скрещиваются с b; в) пересекаются или скрещиваются с b. 4. SA2 = 15 см; SB2 = 18 см; A1C1 = 4 см. 5*. а) 10; б) 15. В2. 1. Прямая a может пересекать прямые m и n в точке их пересечения или в различных точках данных прямых; может пересекать одну из них и быть параллельной другой; может скрещиваться с каждой из них. 3. а) c пересекается или скрещивается с a; б), в) пересекается, параллельна или скрещивается с a. 4. BC = . 5*. а) 10; б) 15.

В1. 1. а) ; б) ; в) . 3. a(2+). В2. 1. а) ; б) ; в) . 3. .

В1. 1. 900. 2. Прямоугольные. 3. Угол KLM – тупой. В2. 1. 900. 2. Треугольник DEK тупоугольный, остальные прямоугольные. 3. Угол H или угол P – прямой.

В1. 1. 300. 2. 1 см. 3. . 4. 400. В2. 1. 600. 2. . 3. . 4. 1050.

В1. 1. а) Да; б) нет. 2. 450. 4. . В2. 1. а) Да; б) нет. 2. 900. 4. .

В1. 1. 64 см2. 2. . 3. . 4. Боковое ребро такой призмы равно 4,8 см; радиус равен 2,4 см. В2. 1. 17 см. 2. . 3. 1,5 дм. 4. Высота такой призмы равна 6 см; радиус равен 3 см. 5*. В центре основания пирамиды.

В1. 2. 6 см. 3. R, 2R. 4. а) 3; б) 3. 5*. 14 см. В2. 2. 25 см. 3. см. 4. а) 3; б) 3. 5*. 300.

В1. 1. см3. 2. 48дм3. 3. . 4. 100 см3. 5*. . В2. 1. p см3. 2. 360. 3. 48 см3. 4. . 5*. .

В1. 1. 1:4. 2. . 3. 20 см2. 4. 8дм2. 5*. 32 см2. В2. 1. . 2. . 3. дм2. 4. 8см2. 5*. 117 см2.

🎥 Видео

6 класс, 3 урок, Длина окружности и площадь кругаСкачать

Построение линии пересечения поверхности шара с проецирующей плоскостиСкачать

Геометрия 11 класс (Урок№8 - Сфера и шар.)Скачать

Цилиндр, конус, шар, 6 классСкачать

Длина окружности и площадь круга | Математика 6 класс #24 | ИнфоурокСкачать

Площадь круга. Математика 6 класс.Скачать

Деление окружности на 3; 6; 12 равных частейСкачать