- Ваш ответ
- решение вопроса
- Похожие вопросы
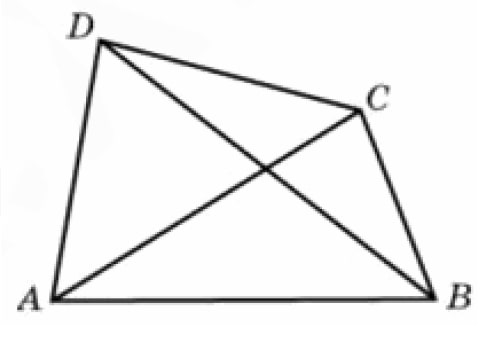
- Решение №636 Диагонали четырехугольника равны 7 и 10.
- В А D С Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника. — презентация
- Похожие презентации
- Презентация на тему: » В А D С Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.» — Транскрипт:
- 📺 Видео
Видео:Диагонали четырехугольника равны 4 и 5.Скачать

Ваш ответ
Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

решение вопроса
Видео:ЕГЭ Математика Задание 6#27845Скачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,701
- разное 16,822
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:ЕГЭ ПЛАНИМЕТРИЯ ДИАГОНАЛИ ЧЕТЫРЕХУГОЛЬНИКА | КАЙФОВЫЙ ЛАЙТОВЫЙ СПОСОБ | ГАРМАШУКСкачать

Решение №636 Диагонали четырехугольника равны 7 и 10.
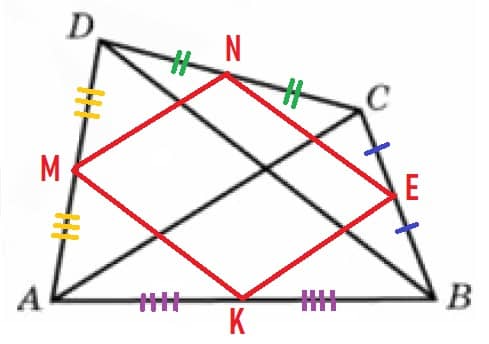
Диагонали четырехугольника равны 7 и 10. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Стороны четырёхугольника MNEK, являются средними линиями соответствующих треугольников и равны половине оснований Δ:
MN = AC/2= 7/2 = 3,5
KE = AC/2= 7/2 = 3,5
MK = DB/2= 10/2 = 5
NE = DB/2= 10/2 = 5
Периметр равен:
P = MN + KE + MK + NE = 3,5 + 3,5 + 5 + 5 = 17
Ответ: 17.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Видео:ЕГЭ 2017 | Задание 3 | Диагонали четырехугольника равны ... ✘ Школа ПифагораСкачать

В А D С Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника. — презентация
Презентация была опубликована 8 лет назад пользователемschool4.vx6.ru
Похожие презентации
Видео:Периметр прямоугольника. Как найти периметр прямоугольника?Скачать

Презентация на тему: » В А D С Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.» — Транскрипт:
1 В А D С Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника. E F Q Р 4 5 Применим свойство средней линии треугольника. QP = 5 : 2 = 2,5 QP – средняя линия треугольника ADC EF = 5 : 2 = 2,5 EF – средняя линия треугольника ABC PF = 4 : 2 = 2 PF – средняя линия треугольника DBC QE = 4 : 2 = 2 QE – средняя линия треугольника DBA P = (2,5+2)*2 = х 1 0 х В 4 9
2 Открытый банк заданий по математике b a (a+b) : 2
3 В А D С В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию F E O OBE – равнобедренный BE = OE OFC – равнобедренный FO = FC DC = 2FO AB = 2OE DC + AB = 2FO + 2OE = 2 FE = 24 (DC + AB) : 2 = 24 : 2 = 12 Средняя линия трапеции равна полусумме оснований+2. 3 х 1 0 х В 4 1 2
4 В А D С Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции F E EL = 1,5 FL = 1 EF = 0,5–3 2L Применим свойство средней линии треугольника. FL = 2 : 2 = 1 FL – средняя линия треугольника BDC EL = 3 : 2 = 1,5 EL – средняя линия треугольника ABC F – середина DB по условию L – середина СВ по теореме Фалеса 3. 3 х 1 0 х В 4 0, 5
5 В А D С Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции. L E 2F EL = = 7 EL – средняя линия треугольника ADC 4. x x+2 Это значит, что один из отрезков НА 2 больше другого. x + x + 2 = 12 x = 5 AB = 7 * 2 = 14 3 х 1 0 х В 4 1 4
6 В А D С Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции. F E 5. x x+4 x + x + 4 = 14 2x = 10 Средняя линия трапеции равна полусумме оснований * 2 x = 5 AB = 9 3 х 1 0 х В 4 9
7 Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции А D С F E Средняя линия трапеции равна полусумме оснований. * 2 x x x B 2x 2x + x + x = 80 4 x = 80 x = 20 3 х 1 0 х В Периметр равен 80
8 Основания трапеции относятся как 2 : 3, а средняя линия равна 5. Найдите меньшее основание.7. В А D С F E 2x2x2x2x 3x3x3x3x 2x + 3x = 10 5x = 10 Средняя линия трапеции равна полусумме оснований * 2 x = 2 DC = 4 3 х 1 0 х В 4 45 Пусть х – 1 часть
9 Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции.8. В А D С F E Сумма непараллельных сторон равна 20. Значит, можно найти сумму параллельных сторон. 3 х 1 0 х В – 20 = 30 сумма параллельных сторон, т.е. сумма оснований30
10 Основания равнобедренной трапеции равны 15 и 9, один из углов равен Найдите высоту трапеции.9. А DС В равнобедренной трапеции построим две высоты. Получим два равных прямоугольных треугольника и прямоугольник. 3 х 1 0 х В 4 3 F 45 0 E AF = (15 – 9) : 2 = 3 B 3 Треугольник прямоугольний и равнобедренный
11 В А D С Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции E 10 F В равнобедренной трапеции построим вторую высоту. Получим два равных прямоугольных треугольника и прямоугольник – 4 = 6 отрезок EF 6 Средняя линия трапеции равна полусумме оснований 3 х 1 0 х В = 14
12 В А DС Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции. E P ADE = P ABCD = DC + CB + BE + EA + AD = DE DE + EA + AD =15 = 23 3 х 1 0 х В 4 2 3
13 В равнобедренной трапеции основания равны 12 и 27, острый угол равен Найдите ее периметр. 12. В А D С 12 E F В равнобедренной трапеции построим вторую высоту. Получим два равных прямоугольных треугольника и прямоугольник. (27 – 12) : 2 = 7,5 отрезки AF, BE 3 х 1 0 х В ,5
14 В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними Найдите меньшее основание В А D С E F В равнобедренной трапеции построим вторую высоту. Получим два равных прямоугольных треугольника и прямоугольник. 25 – (5+5) = 15 отрезки EF и DC 3 х 1 0 х В
15 Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.14. В А D С E F L EL = 10 : 2 = 5 EL – средняя линия треугольника ADB FL = 4 : 2 = 2 FL – средняя линия треугольника DBC 3 х 1 0 х В
16 Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции В А D С E F 3 х 1 0 х В Средняя линия трапеции равна полусумме оснований.1828 * 2
17 Найдите среднюю линию трапеции, если ее основания равны 30 и В А D С E F 3 х 1 0 х В Средняя линия трапеции равна полусумме оснований.
18 Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 50 0 ? Ответ дайте в градусах В А DС x x+50 Это значит, что один из углов НА 50 0 больше другого. В равнобедренной трапеции углы при основании равны x x+50 x + x + 50 =180 сумма односторонних углов при параллельных прямых равна 180 0, AB II DC, AD — секущая 2x + 2(x + 50) =360 сумма углов четырехугольника способ 2 способ x = 65 Тогда тупой уго трапеции равен = х 1 0 х В
📺 Видео
8 класс, 3 урок, ЧетырехугольникСкачать

Геометрия Найдите диагональ четырехугольника, если его периметр равен 80 см, а периметрыСкачать

как найти диагональ.Скачать
Периметр треугольника. Как найти периметр треугольника?Скачать

38. Геометрия на ЕГЭ по математике. Задача на тему "Средняя линия треугольника"Скачать

ОГЭ по математике. Площадь четырехугольника можно вычислить по формуле (вар. 5)Скачать

Сложные примеры с поиском периметра 3 задание проф. ЕГЭ по математикеСкачать

Периметр квадрата. Как найти периметр квадрата?Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

№564. Дан треугольник, стороны которого равны 8 см, 5 см и 7 см. Найдите периметр треугольника,Скачать

№502. Высоты параллелограмма равны 5 см и 4 см, а периметр равен 42 см. Найдите площадь параллелограСкачать

Задание 3 ЕГЭ по математике. Урок 46Скачать

Геометрия Сумма диагоналей четырехугольника равна 28 см. Найдите периметр четырехугольника, вершиныСкачать

Геометрия 8. Урок 12 - Площадь четырехугольников. Формулы.Скачать