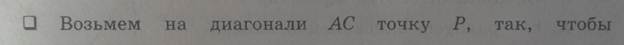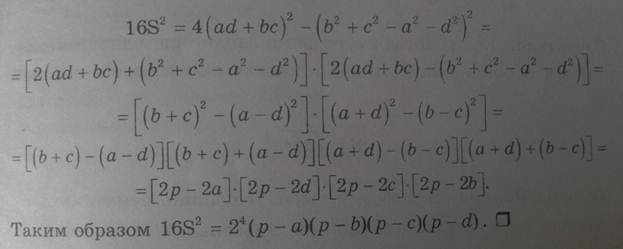2021-07-22 
Докажите, что диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов его противоположных сторон равны.
Первый способ. Необходимость. Пусть диагонали $AC$ и $BD$ четырёхугольника $ABCD$ перпендикулярны. Если $P$ их точка пересечения, то по теореме Пифагора
Аналогично докажем, что
Достаточность. Пусть в четырёхугольнике $ABCD$ известно, что
Рассмотрим отрезок $AC$. Известно, что геометрическое место точек $X$, для которых разность $AX^-CX^$ постоянна, есть прямая, перпендикулярная отрезку $AB$ (см. задачу @H2445). Поскольку точки $B$ и $D$ удовлетворяют этому условию, они лежат на этой прямой. Следовательно, $ACperp BD$.
Второй способ. Необходимость. См. первый способ.
Достаточность. Пусть в четырёхугольнике $ABCD$ известно, что
а диагонали $AC$ и $BD$ пересекаются в точке $P$. Обозначим
а т.к. по условию $AB^+CD^=BC^+AD^$, то
причём $ab+cd+bc+adne0$. Следовательно, $cosalpha=0$ и $ACperp BD$.
Третий способ. Для любых точек $A$, $B$, $C$ и $D$ плоскости (пространства) верно равенство
Видео:№521. Докажите, что если диагонали четырехугольника ABCD взаимно перпендикулярны, то AD2 +ВС2 =AB2+CСкачать
Диагонали четырехугольника перпендикулярны когда суммы квадратов
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Различают выпуклые и невыпуклые и звездчатые четырёхугольники. Выпуклым четырехугольником называется четырехугольник, у которого все углы меньше развернутого угла. Четырехугольник, у которого угол больше развернутого называется невыпуклым
Виды четырёхугольников
Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
Прямоугольник — четырёхугольник, у которого все углы прямые;
Ромб — четырёхугольник, у которого все стороны равны;
Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
(Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.)
- Сумма углов четырёхугольника равна 2 π = 360°.
- Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° (). См. также теорема Птолемея.
- Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ()
- Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
- Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
- Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
- Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.
Теорема Вариньона
Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника.
или сокращённо
Середины сторон произвольного четырёхугольника — вершины параллелограмма
Доказательство
Проведём диагональ AC. Отрезки EF и GH будут средними линиями треугольников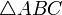 
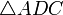
и 
. По теореме о средней линии, отрезки будут параллельны диагонали, а, значит, и друг другу. Повторив аналогичные рассуждения для диагонали BD, получаем, что противоположные стороны четырёхугольника EFGH параллельны, и, по определению, это — параллелограм.
Доказательство, что площадь параллелограмма равна половине площади исходного четырехугольника: Пусть диагональ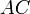 
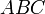
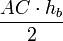
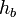
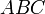
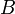
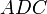
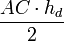
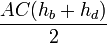
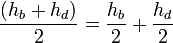
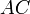
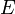
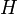
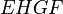
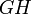
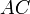
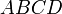
проходит внутри четырёхугольника. Тогда площадь треугольника 
равна 
, где 
— высота треугольника 
, проведённая из вершины 
. Аналогично, площадь треугольника 
равна 
. Тогда площадь всего четырёхугольника равна 
. Но 
— это сумма расстояний до прямой 
от точек 
и 
, то есть в точности высота параллелограмма 
. А поскольку сторона 
параллелограмма вдвое меньше 
, то и площадь параллелограмма равна половине площади 
,
Теорема Эйлера
в любом четырехугольнике сумма квадратов сторон равна сумме квадратов диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналями
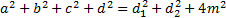
Следствие: Сумма квадратов длин равна диагоналей параллелограмма равна сумме квадратов длин его сторон
Теорема Птолемея
Для любого выпуклого четырёхугольника ABCD вписанного в окружность, сумма произведений длин противоположных сторон равна произведению длин диагоналей AB*DC+BC*AD=BD*AC
Теорема Брахмагупты(площадь вписанного в окружность четырёхугольника)
Если a, b, c, d – длины сторон четырёхугольника,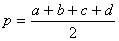 
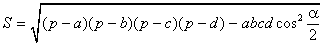
– его полупериметр, а α – сумма его противоположных углов, то площадь Sчетырёхугольника равна 
.
В качестве α здесь можно взять сумму любой из двух пар противоположных углов, результат от этого не зависит. В случае четырёхугольника, вписанного в окружность, эта формула принимает более простой вид: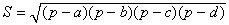 
;
это равенство и называется формулой Брахмагупты. Если четырёхугольник имеет и описанную и вписанную окружности, то формула становится совсем короткой: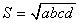 
.
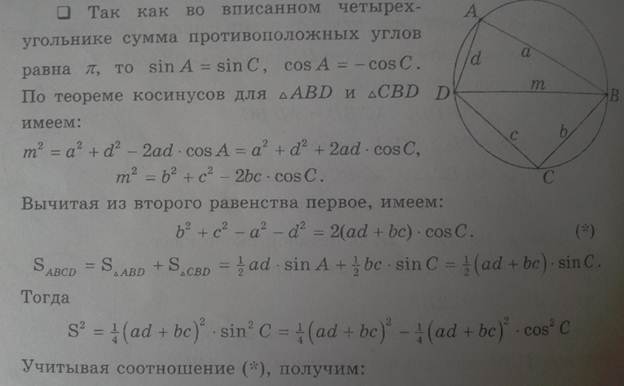
Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать
Please wait.
Видео:Сумма квадратов диагоналей параллелограммаСкачать
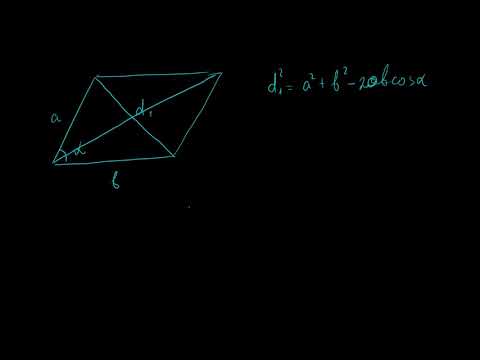
We are checking your browser. mathvox.ru
Видео:№520. Диагонали равнобедренной трапеции взаимно перпендикулярны, а сумма ее оснований равна 2аСкачать
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:№410. Является ли четырехугольник квадратом, если его диагонали: а) равны и взаимноСкачать
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6c6549eeb9537b7b • Your IP : 178.45.231.185 • Performance & security by Cloudflare
🌟 Видео
Диагонали четырехугольника равны 4 и 5.Скачать
Диагонали квадрата взаимно перпендикулярны. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать
№478. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадьСкачать
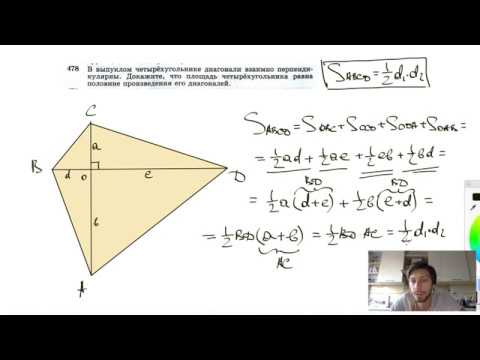
Если в четырёхугольнике диагонали перпендикулярны ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
Диагонали четырёхугольника ABCD, вписанного в окружность, взаимно перпендикулярны. Из вершин В и ССкачать
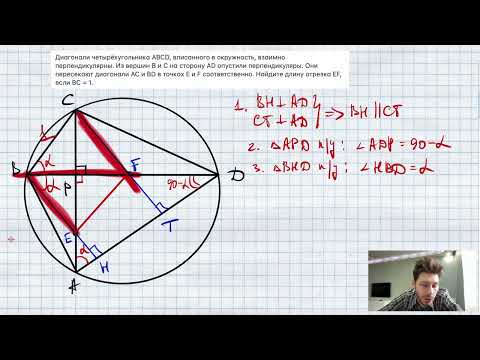
№129. Прямая AM перпендикулярна к плоскости квадрата ABCD, диагонали которого пересекаютсяСкачать
Если диагонали выпуклого четырёхугольника равны ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
Один отрезок - диагональ четырёхугольника, диаметр окружности, высота ромбаСкачать
Геометрия Диагонали AC и BD параллелограмма ABCD равны соответственно 24 см и 10 см AD = 13 смСкачать
Свойства диагоналей параллелограмма | Геометрия 8-9 классыСкачать
Геометрия Диагонали четырехугольника ABCD вписанного в окружность перпендикулярны, угол ACB = 10Скачать
Геометрия Докажите что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех егоСкачать
Решаем геометрию. Планиметрия 3.7Скачать
Геометрия 10 класс (Урок№2 - Четырехугольники.)Скачать
