Задание. Диагонали AC и BD четырехугольника ABCD, вписанного в окружность, пересекаются в точке Р, причем BC = CD.
а) Докажите, что AB : BC = AP : PD.
б) Найдите площадь треугольника COD, где О – центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD – диаметр описанной около четырехугольника ABCD окружности, АВ = 5, а ВС = 5√2.
Рассмотрим треугольники ∆ABC и ∆APD. Вписанные углы ∠BAC = ∠CAD, так как опираются на равные хорды (BC = CD). Вписанные углы ∠ACB = ∠ADB, так как опираются на одну и ту же дугу АВ. Следовательно, треугольники ∆ABC и ∆APD подобные треугольники. Тогда
б) Найдите площадь треугольника COD, где О – центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD – диаметр описанной около четырехугольника ABCD окружности, АВ = 5, а ВС = 5√2.
Так как BD – диаметр окружности, то вписанный угол ∠BCD = 90°, следовательно, треугольник ∆BCD – прямоугольный равнобедренный треугольник. По теореме Пифагора найдем BD:
BD 2 = BC 2 + CD 2
BD 2 = (5√2) 2 + (5√2) 2 = 100
Так как BD – диаметр окружности, то вписанный угол ∠BAD = 90°, следовательно, треугольник ∆BAD – прямоугольный треугольник. В прямоугольном треугольнике ∆BAD гипотенуза BD = 10, катет АВ = 5.
По свойству прямоугольных треугольников: если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
Следовательно, угол ∠ADB = 30°, а угол ∠ABD = 60°.
Вписанные углы ∠ABD = ∠ACD, так как опираются на одну и ту же дугу АD, значит, ∠ABD = ∠ACD = ∠ОCD = 60°.
Точка О – центр вписанной в треугольник ∆ABD окружности. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис. Тогда точка О лежит на биссектрисе АС угла ∠BAD и на биссектрисе OD угла ∠ADВ.
Так как угол ∠ADB = 30°, то угол ∠ADO = ∠ODB = 15°. Так как угол ∠BAD = 90°, то угол ∠BAO = ∠OAD = 45°.
Угол ∠СОD – внешний угол треугольника ∆AOD, следовательно, ∠СOD = ∠OAD + ∠ADO = 45° + 15° = 60°. Угол ∠СOD = 60°. Тогда треугольник ∆COD – равносторонний треугольник, в котором OC = OD = CD = 5√2.
Найдем площадь треугольника ∆COD:
Ответ:
Видео:Диагонали АС и BD четырехугольника...Скачать

Диагонали ac и bd четырехугольника abcd вписанного в окружность пересекаются в точке к найдите
Задание 16. Диагонали АС и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC = CD.
а) Докажите, что AB:BC=AP:PD.
б) Найдите площадь треугольника COD, где О — центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, АВ = 5, а ВС = 5√2.
а) Так как стороны BC=CD, то и дуга BC равна дуге CD. На эти дуги опираются равные углы: BAC, CAD, CBD, CDB. Получаем подобные треугольники BPC и APD (по двум углам), следовательно, 


Далее, треугольники BPC и ABC также подобны по двум углам, поэтому


В результате из (1) и (2), имеем:
б) Так как BD – диаметр окружности, то треугольники BCD и ABD – прямоугольные с прямыми углами C и A соответственно. Также по условию задания BC=CD=5√2, получаем
Рассмотрим прямоугольный треугольник BAD, в котором AB=5, BD=10, следовательно, угол BDA=30°, а угол ODO1 = 15° (так как O – центр вписанной окружности, поэтому DO – биссектриса).
Далее, из равнобедренного треугольника BCD с основание BD получаем, что угол CDB=45°, следовательно, угол ODC=45+15=60°. Из прямоугольного треугольника ABD
и полупериметр треугольника ABD, равен:
Найдем отрезок DE=p-AB (как отрезок части касательной), имеем:
и радиус вписанной окружности:
Рассмотрим прямоугольный треугольник OED, из которого
Рассмотрим треугольник OCD, в котором 
Ответ:
Видео:Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ| Подобные треугольникиСкачать

Решение №2427 Четырёхугольник ABCD со сторонами АВ = 40 и CD = 10 вписан в окружность.
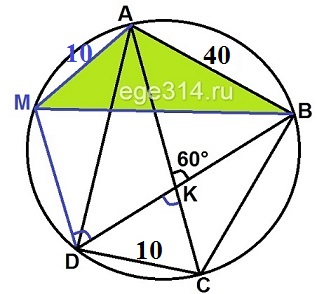
Четырёхугольник ABCD со сторонами АВ = 40 и CD = 10 вписан в окружность. Диагонали АС и BD пересекаются в точке K, причём ∠AKB = 60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Источник: ОГЭ Ященко 2022 (36 вар)
Проведём прямую DM параллельную АС. Дуги ‿АМ = ‿DC, значит и хорды равны DC = AM = 10.
∠ABK = ∠DKC = 60°, как вертикальные. ∠MDK = ∠DKC = 60°, как накрест лежащие углы, при AC||MD и секущей DK.
Четырёхугольник AMDB вписан в окружность, сумма противоположных углов равна 180°. Найдём ∠MAB:
∠MAB = 180° – ∠MDB = 180° – 60° = 120°
По теореме косинусов найдём MB:
MB 2 = AM 2 + AB 2 – 2·AM·AB·cos 120°
Найдём радиус описанной вокруг ΔABM окружности по теореме синусов:
Ответ: .
💥 Видео
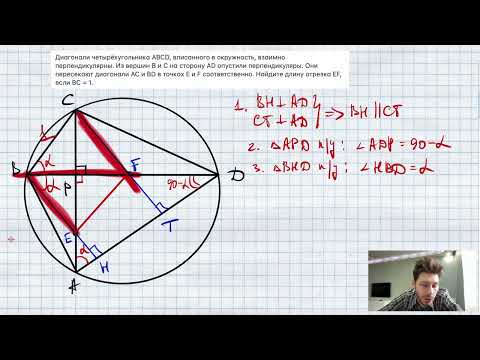
Диагонали четырёхугольника ABCD, вписанного в окружность, взаимно перпендикулярны. Из вершин В и ССкачать
Геометрия Четырёхугольник ABCD со сторонами AB = 2 и CD = 5 вписан в окружность. Диагонали AC и BDСкачать

ОГЭ по математике. Задание 16Скачать

№1039. Диагонали квадрата ABCD пересекаются в точке О. Найдите угол между векторами: а) АВ и АССкачать

Решение задачи 25 из ОГЭ по математике 9 классСкачать

Четырёхугольник ABCD со сторонами AB = 40 и CD = 10 вписан в окружность. Диагонали #огэ #математикаСкачать

№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать

Хорды AC и BD окружности пересекаются в точке P, BP=6, CP=8, DP=12. Найдите AP.Скачать

Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

ЗАДАНИЕ 1| ЕГЭ ПРОФИЛЬ| Угол А четырёхугольника ABCD, вписанного в окружность, равен 25.Найдите уголСкачать

3.25.1. Планиметрия. Гордин Р.К.Скачать

ОГЭ по математике. Задание 15Скачать
Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC = 12, AB = 7. Найдите DO.Скачать

3 правила для вписанного четырехугольника #shortsСкачать

ОГЭ 2020 задание 18Скачать

ОГЭ без рекламы математика 11 и 12 вариант задача 25Скачать

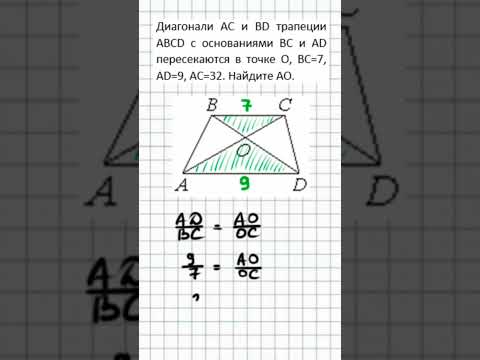
№552. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите:Скачать

ОГЭ 2020 задание 18Скачать