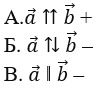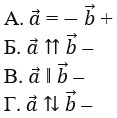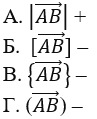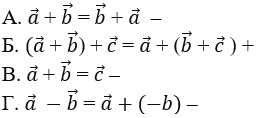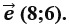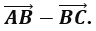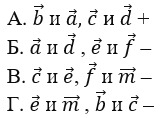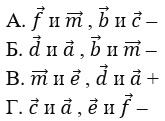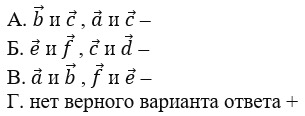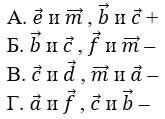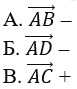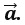Действия с векторами самостоятельная работа

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Зачётная работа по геометрии №1

1. Даны векторы:

Постройте: 1) а + m ( по правилу треугольника);

m

2) n + a ( по правилу параллелограмма);

a n 3) m — n ;

4) 2 a — 3 m + 0,5 n ; 5) 0 m

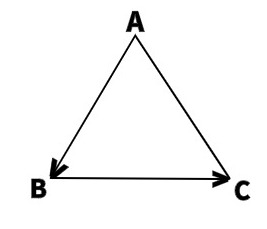
2. О- точка пересечения медиан треугольника АВС . А D – одна из медиан,

АВ = с , АС = b . Выразите через данные векторы: ВС, ОА, О D , АВ – ОС.

3. Точки M, N, K, L – середины сторон АВ, ВС, С D , AD прямоугольника

АВС D . АВ = а, AD = b . Выразить через данные векторы: АМ + А N ; АМ – А N .

4. ABCD – трапеция, AD || BC , AC = m , DB = n . Выразите через данные векторы:

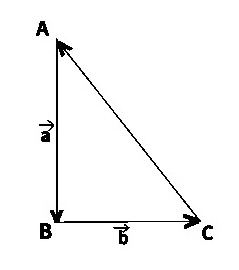
АВ — D В + DC -АС; А D + BC , АВ – А D + BA — BC .

Зачётная работа по геометрии №1

1. Даны векторы:

Постройте: 1) а + m ( по правилу треугольника);

m

2) n + a ( по правилу параллелограмма);

a n 3) m — n ;

4) 2 a — 3 m + 0,5 n ; 5) 0 m

2. О- точка пересечения медиан треугольника АВС . А D – одна из медиан,

АВ = с , АС = b . Выразите через данные векторы: ВС, ОА, О D , АВ – ОС.

3. Точки M, N, K, L – середины сторон АВ, ВС, С D , AD прямоугольника

АВС D . АВ = а, AD = b . Выразить через данные векторы: АМ + А N ; АМ – А N .

4. ABCD – трапеция, AD || BC , AC = m , DB = n . Выразите через данные векторы:

АВ — D В + DC -АС; А D + BC , АВ – А D + BA — BC .

Самостоятельная работа. Действия над векторами

Самостоятельная работа по теме: «Действия над векторами»

Даны векторы и . Найдите координаты суммы этих векторов.

Дан вектор . Найдите координаты вектора, равного –4.

Даны векторы и . Найдите координаты векторов

Даны векторы и . Найдите координаты разности этих векторов.

Самостоятельная работа по теме: «Действия над векторами»

Даны векторы и . Найдите координаты суммы этих векторов.

Дан вектор . Найдите координаты вектора, равного –3.

Даны векторы и . Найдите координаты векторов

Даны векторы и . Найдите координаты разности этих векторов.

Самостоятельная работа по теме: «Действия над векторами»

Даны векторы и . Найдите координаты суммы этих векторов.

Дан вектор . Найдите координаты вектора, равного –4.

Даны векторы и . Найдите координаты векторов

Даны векторы и . Найдите координаты разности этих векторов.

Самостоятельная работа по теме: «Действия над векторами»

Даны векторы и . Найдите координаты суммы этих векторов.

Дан вектор . Найдите координаты вектора, равного –3.

Даны векторы и . Найдите координаты векторов

Даны векторы и . Найдите координаты разности этих векторов.

Самостоятельная работа по теме: «Действия над векторами»

Даны векторы и . Найдите координаты суммы этих векторов.

Дан вектор . Найдите координаты вектора, равного –4.

Даны векторы и . Найдите координаты векторов

Даны векторы и . Найдите координаты разности этих векторов.

Самостоятельная работа по теме: «Действия над векторами»

Даны векторы и . Найдите координаты суммы этих векторов.

Дан вектор . Найдите координаты вектора, равного –3.

Даны векторы и . Найдите координаты векторов

Даны векторы и . Найдите координаты разности этих векторов.

Самостоятельная работа по теме: «Действия над векторами»

Даны векторы и . Найдите координаты суммы этих векторов.

Дан вектор . Найдите координаты вектора, равного –4.

Даны векторы и . Найдите координаты векторов

Даны векторы и . Найдите координаты разности этих векторов.

Самостоятельная работа по теме: «Действия над векторами»

Даны векторы и . Найдите координаты суммы этих векторов.

Дан вектор . Найдите координаты вектора, равного –3.

Даны векторы и . Найдите координаты векторов

Даны векторы и . Найдите координаты разности этих векторов.

Самостоятельная работа по теме: «Действия над векторами»

Даны векторы и . Найдите координаты суммы этих векторов.

Дан вектор . Найдите координаты вектора, равного –4.

Даны векторы и . Найдите координаты векторов

Даны векторы и . Найдите координаты разности этих векторов.

Самостоятельная работа по теме: «Действия над векторами»

Даны векторы и . Найдите координаты суммы этих векторов.

Дан вектор . Найдите координаты вектора, равного –3.

Даны векторы и . Найдите координаты векторов

Даны векторы и . Найдите координаты разности этих векторов.

—> —>

АвторДата добавленияРазделПодразделПросмотровНомер материала

Просвирнина Екатерина Михайловна

16.10.2019

Геометрия

Самостоятельная работа

1552

6358

© 2022 Проект «Уроки математики»

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

Действия с векторами самостоятельная работа

Тесты по геометрии 9 класс. Тема: «Векторы»

Правильный вариант ответа отмечен знаком +

1. Отрезок, для которого указано, какой из его концов является началом, а какой – концом, называется:

Г. нет верного варианта ответа –

2. Любая точка пространства может рассматриваться как вектор. Такой вектор называется:

3. Два ненулевых вектора, лежащие на одной прямой или на параллельных прямых, называются:

В. противоположно направленными –

4. Какие слова пропущены в предложении?

Если два ненулевых вектора коллинеарны, то они могут быть направлены либо одинаково (тогда их называют …), либо противоположно (тогда их называют …).

А. сонаправленные; разнонаправленные –

Б. противоположно направленные: сонаправленные –

В. сонаправленные: противоположно направленные +

Г. нет верного варианта ответа –

5. Длиной ненулевого вектора 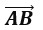называется:

Б. длина отрезка AB +

Г. нет верного варианта ответа –

6. Выберите верное обозначение сонаправленных векторов.

Г. нет верного варианта ответа –

7. Векторы называются равными, если:

А. они коллинеарны –

Б. их длины равны –

В. они сонаправлены –

Г. они сонаправлены и их длины равны +

8. Выберите верное обозначение противоположных векторов.

9. Выберите верное обозначение длины вектора

тест 10.

11. – это формула:

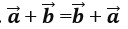
А. разности вектора –

Б. сочетательного закона –

В. нет верного варианта ответа –

Г. переместительного закона +

12. Выберите верную формулу сочетательного закона.

13. Вектор отложен от точки M. Точка M является:

А. концом вектора –

Б. началом вектора +

В. серединой вектора –

Г. нет верного варианта ответа –

14. Если длины двух ненулевых векторов равны, и они противоположно направлены, то они называются:

15. ABC – прямоугольный треугольник, 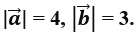Найдите длину вектора

16.

17. Найдите длину вектора

18. Дан правильный треугольник ABC со стороной 2. Найдите длину вектора

Г. недостаточно данных –

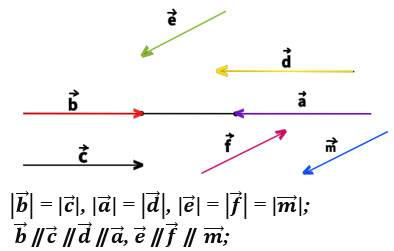
19. Выберите пары противоположно направленных векторов.

тест-20. Выберите пары сонаправленных векторов.

21. Выберите пары противоположных векторов.

22. Выберите пары равных векторов.

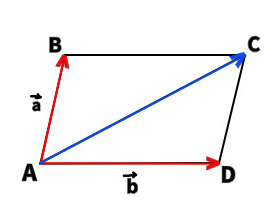
23. Дан параллелограмм ABCD, AC – диагональ Найдите сумму векторов

Г. нет верного варианта ответа –

24. Выберите верную формулировку правила многоугольника.

А. Чтобы сложить несколько векторов, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее; когда все векторы отложены, соединив начальную точку с концом последнего вектора, получим сумму нескольких векторов. +

Б. От любой точки можно отложить вектор, равный данному, и притом только один. –

В. Чтоб сложить два вектора, нужно из произвольной точки отложить один вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало одного с концом второго. –

Г. Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти два вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, и будет суммой заданных векторов. –

25. Верны ли следующие суждения?

а. Векторы называются равными, если они коллинеарные и их длины равны.

б. Длиной нулевого вектора 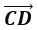является длина отрезка CD.

А. верно только а –

Б. верно только б +

В. оба суждения верны –

Г. оба суждения неверны –

26. Верны ли следующие суждения?

а. Направленный отрезок (вектор), длина которого равна нулю, – это нулевой вектор.

б. От любой точки можно отложить вектор, равным данному, и притом только один.

А. верно только а –

Б. верно только б –

В. оба суждения верны +

Г. оба суждения неверны –

27. Верны ли следующие суждения?

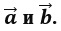
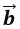
а. Разностью векторов называется такой вектор, сумма которого с вектором равна вектору

б. Два ненулевых вектора называются коллинеарными, если их длины равны и они противоположно направлены.

А. верно только а +

Б. верно только б –

В. оба суждения верны –

Г. оба суждения неверны –

28. Верны ли следующие суждения?

А. верно только а –

Б. верно только б +

В. оба суждения верны –

Г. оба суждения неверны –

29. Верны ли следующие суждения?

а. Вектор называется нулевым, если его начальная и конечная точка совпадает.

б. Модулем вектора называется длина вектора, выраженная числовым выражением.

А. верно только а –

Б. верно только б –

В. оба суждения верны +

Г. оба суждения неверны –

тест_30. Верны ли следующие суждения?

а. Скалярные величины характеризуются числом и направлением, а векторные только числом.

б. К векторным величинам относятся скорость, ускорение, перемещение.

💡 Видео